轨道转移航天器紫外自主导航的应用*
2017-11-20潘静姚宏瑛
潘静,姚宏瑛
(中国航天科工集团第二研究院 七〇六所,北京 100854)
轨道转移航天器紫外自主导航的应用*
潘静,姚宏瑛
(中国航天科工集团第二研究院 七〇六所,北京 100854)
应用紫外敏感器可较高精度地实现航天器全程自主导航。为解决其应用于中高轨不全程可见以及地心距测量误差大的问题,将紫外敏感器采用中心视场和环形视场同轴的结构,用中心视场观测地球,仅以地心方向矢量作为观测量降维输出,采用扩展卡尔曼滤波算法估计出航天器的位置和速度。对该方案建立算法模型,以轨道高度1 000~36 000 km的转移轨道为例仿真验证,研究测量精度、采样周期对导航精度的影响,分析系统可观性。仿真结果表明,系统可观,紫外敏感器测量精度越高导航精度越高,地心方向测量误差不大于0.05°时导航精度位置误差不超过4 km、速度误差不超过0.5 m/s,方案有效可行。
自主导航;紫外敏感器;轨道转移;地心矢量;降维;扩展卡尔曼滤波
0 引言
空间已成为维护国家安全和国家利益必须关注和占领的战略制高点。随着航天任务的发展,航天器需要实时、高精度地确定自身的位置和姿态信息,这对自主导航提出了迫切的要求。航天器自主导航是指航天器在不依赖地面支持的情况下,通过其自身所携带的测量设备确定航天器的位置和速度[1]。自主导航有利于降低航天器对地面的依赖程度,提高系统的生存能力,轻小型、高精度、长航时、全自主是其发展方向。
自20世纪60年代以来,国外就开始研究航天器基于星体敏感器的自主导航方案。与此同时,不断发展与各种自主导航系统方案相适应的各种敏感器,包括地球敏感器、太阳敏感器、CCD星敏感器、自动空间六分仪等[2]。紫外敏感器更是近些年来的研究热点,其体积小、质量轻、成本低、精度高等特点,使其具有无可比拟的优势。基于紫外敏感器的天文导航技术极具研究价值与发展潜力,是提高航天器自主导航系统性能的极佳选择。
Holleywell公司从1992年开始研制地球基准姿态确定系统(ERADS),用一个紫外敏感器同时提供卫星的三轴姿态数据和自主导航数据,是小卫星关键技术的一项重要突破[3]。NASA的Goddard空间飞行中心在1996年研制了基于瑞丽散射的紫外地球敏感器,并进行了搭载实验[4]。中国空间技术研究院在2009年设计研制了应用于地月转移轨道慢旋探测器的紫外地球月球敏感器[5]。
由于紫外敏感器视场角的范围限制,基于紫外敏感器的自主导航多用于低轨卫星。本文针对中轨到高轨的轨道转移航天器应用(轨道高度范围为1 000~36 000 km),仅以地心方向作为观测量设计了一种基于紫外敏感器的自主导航方案,并通过仿真验证其有效性。
1 导航原理
1.1紫外敏感器
紫外敏感器是一种基于感受天体紫外线辐射获得航天器位置和姿态信息的成像式敏感器,工作波段为 270~300 nm。空间的紫外线辐射来自地球边缘的大气层和太阳、恒星等天体。由于大气中的氧和臭氧形成波长小于 300 nm 的强吸收带,在地面和大气特征以上的高度形成球日照边缘,且此日照边缘不受地面和气象特征的影响,因此在紫外波段能探测出整个地球边缘的图像,其图像稳定性可与红外图像媲美。同时紫外波段也是观测导航星的极佳光谱波段[6]。
紫外敏感器体积小、质量轻、功耗小、精度高,利于系统小型化和微型化的需求,是新一代敏感器的发展方向[7-9]。如图1所示,它具有2个视场:中心视场和外环视场,2个视场通过平面镜反射成像在一块CCD板上。其各项参数对比见于表1。
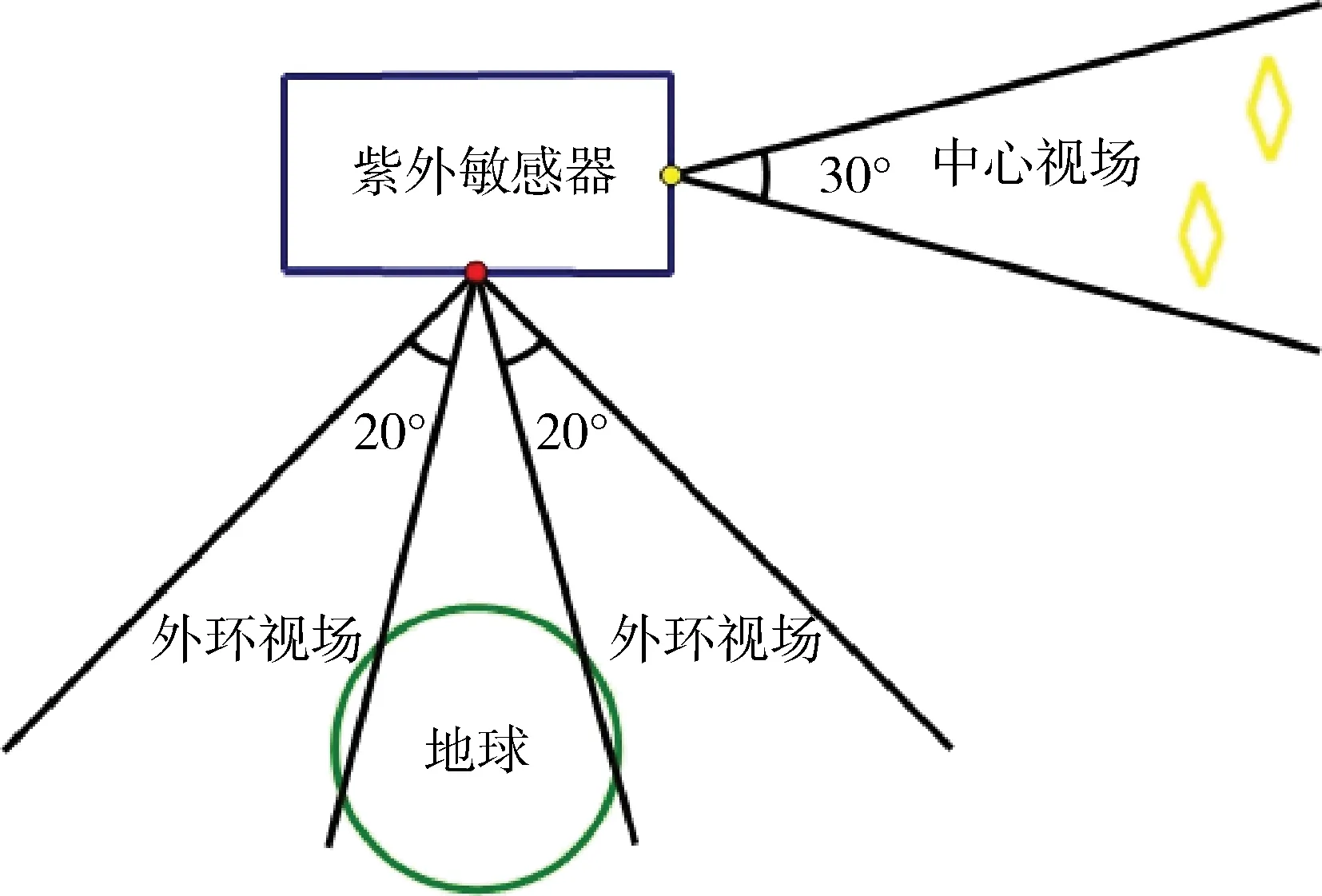
图1 紫外敏感器视场示意图Fig.1 Schematic diagram of the field of ultraviolet sensor

表1 紫外敏感器视场参数对比Table 1 Comparison of field parameters of ultraviolet sensor
中心视场30°,用于观测太阳或恒星的紫外辐射,从而得到恒星在观测坐标系下的坐标,与其在绝对坐标系下的坐标进行运算后,最终确定航天器的三轴姿态。可观测+4.5等以上的星体,数量可达200颗左右,自动识别星图,定姿精度10″(1δ)。
外环视场一般120°~160°,用于观测地球大气层的边缘,图像经处理后得到地心矢量信息(包括地心矢量方向和地心距),经过运算从而确定航天器在轨位置以及速度。基于紫外敏感器的自主导航其精度主要取决于地心方向测量精度,测距误差对导航精度的影响并不十分显著。其中地心测距误差5~5 000 m,地心方向矢量测量误差0.01°~0.2°(1δ)[10-11]。
1.2应用改进
紫外敏感器与航天器固连,其外环视场敏感地球大气边缘的紫外辐射,通过辨识成像整圆的大小和方位,经数据处理得到地心矢量信息(包括地心方向和地心距),进而确定航天器在轨位置以及速度。由于受到外环视场角的限制(一般120°~160°),若要求地球全程可见以实现全程基于紫外敏感器自主导航,航天器运行轨道高度需满足一定条件。如图2所示,轨道高度h,有
R/sinθ2-R≤h≤R/sinθ1-R.
(1)

图2 轨道高度与视场角关系示意图Fig.2 Orbit height and angle relation diagram
紫外敏感器外环视场角一般为120°~160°,即θ1=60°,θ2=80°。由式(1)知,在轨道高度为(98.3,985.6)km的范围内航天器可基于紫外敏感器全程自主导航。故基于紫外敏感器的自主导航多应用于低轨卫星。而对于中高轨航天器,以轨道高度1 000~36 000 km的中高轨轨道转移航天器为例,为实现其全程基于紫外敏感器自主导航,则要求外环视场范围为17°~120°。如此大范围的外环视场需求对于紫外敏感器的生产工艺提出了严峻的挑战。
除此以外,随着轨道高度的增加,地心距逐渐增大,航天器对地球的视场角逐渐减小,即CCD板上成像圆盘的直径越来越小,使得地心距的测量误差逐渐增大。从高度为1 000 km轨道转移到高度为36 000 km轨道,地心距的测量误差从1 000 m逐渐增加到几十km。地心距测量数据可信度大大降低,并且这是个动态随机变化的过程无法定量描述给予补偿,故地心距测量数据不可用。
考虑到上述问题,针对中高轨轨道转移航天器,可将紫外敏感器采用中心视场和环形视场同轴的结构,用中心视场观测地球,用环形视场观测导航恒星,即将地球视为质点,仅以地心方向矢量作为观测量设计基于紫外敏感器的自主导航方案。此方案巧妙使用即有的紫外敏感器,无需额外定制大范围外环视场;而基于紫外敏感器的自主导航其精度主要取决于地心方向测量精度,测距误差对导航精度的影响并不十分显著,故仅以地心方向矢量作为观测量的降维处理在理论上可行。综上,此改进方案同时解决了紫外敏感器应用于中高轨航天器不全程可见和地心距测量误差大的问题。
2 算法模型
2.1坐标系的选取
选取J2000地心赤道惯性坐标系(Oxyz),其定义为:以地心为原点,J2000历元时刻的地球平赤道面为参考面,x轴指向该历元时刻的平春分点,z轴与参考面的正法向方向一致,选择y轴使其与x,z轴垂直形成右手坐标系[12-13]。
本文中模型的建立、数据的运算均在此坐标系下定义。
2.2转移轨道动力学方程
转移轨道又称过渡轨道,是航天器从初始轨道或停泊轨道过渡到工作轨道的中间轨道。如图3所示,从高度为10 00 km的轨道转移到高度为36 000 km的轨道,航天器在初始轨道某位置受到瞬时冲量的作用,速度突变,之后在无任何外加控制力的作用下自由漂移到目标轨道。轨道转移的过程航天器仅受万有引力作用,实际上是二体轨道动力学问题。在地心赤道惯性坐标系中取状态变量X=(x,y,z,vx,vy,vz)T,建立轨道动力学方程,有[2]
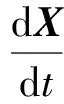
(2)
式中:w为系统噪声,并满足E(w) = 0,E(wwT)=Q。

图3 转移轨道示意图Fig.3 Schematic diagram of transfer orbit
2.3状态方程的建立
对于近地轨道,地球摄动的主要因素是地球的扁状,其他作用力与地球扁状摄动相比都是10-3量级以下的小量[7]。因此,本文在建立系统的状态方程时,考虑地球中心引力和J2摄动项,其他摄动因素等效为高斯白噪声。式(2)在J2000地心赤道惯性坐标系下的三维形式有[2]
(3)



(4)
得到离散的系统状态方程:
Xk=φ(k,k-1)Xk-1+ωk.
(5)
紫外敏感器的输出为地心矢量的大小和方向,仅以地心方向作为观测量,观测方程有

(6)
(7)
式中:νK为量测噪声,并满足E(ν)=0,E(ννT)=R。
2.4滤波算法
采用扩展卡尔曼滤波算法[12-14]:
(8)
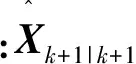
3 仿真分析
3.1方案论证
本文针对从轨道高度1 000 km转移到轨道高度36 000 km的中高轨轨道转移航天器进行仿真,仿真遵循如下条件:
(1) 仿真模型:转移轨道动力学方程;
(2) 参考坐标系:J2000地心赤道惯性坐标系;
(3) 敏感器精度:紫外三轴敏感器的测量精度分别取为0.01°(1δ);
(4) 采样周期:0.1 s;
(5) 测量误差:以白噪声模拟测量误差;
(6) 航天器姿态:假定航天器标称姿态为航天器对地定向且三轴稳定;
(7) 转移轨道参数:半长轴a=26 332 437.9,偏心率e=0.72,轨道倾角i=90°,升交点赤经Ω=0,近地角ω=13.75°,平近点角M=1.89°;
(8) 初始参数:
初始姿态( 0,0,0);
初始位置( 6.509 244 371 304 875e+006, 0, 3.713 244 835 519 765e+006)m;
初始速度(-3.737 397 235 776 740e+003,0,8.790 602 460 568 101e+003)m/s;
初始位置误差(10,10,10)km;初始速度误差(2,2,2)m/s。
根据以上仿真条件,采用模拟的轨道数据和紫外敏感器测量数据,在航天器运行4 h内进行采样,仿真结果见图4。大范围初始误差滤波依旧收敛,表明此自主导航方案对初始误差不敏感。最终导航精度位置误差1.23 km,速度误差0.17 m/s,验证方案有效。
3.2导航精度分析
(1) 紫外敏感器测量精度对导航精度的影响
根据现有工业水平紫外敏感器地心方向测量精度可达0.01°~0.2°(1δ)。分别取地心方向测量精度0.01°,0.02°,0.05°,0.1°,0.2°,研究紫外敏感器测量精度对导航精度的影响。取初始位置误差500 m,初始速度误差0.05 m/s,采样周期0.1 s,仿真结果见表2。可知,紫外敏感器测量精度越高导航精度越高,且地心方向测量误差不大于0.05°时导航精度位置误差不超过4 km、速度误差不超过0.5 m/s。故该自主导航方案具有工业基础和工程基础,与现有工程产品有覆盖,具有可实现性。

表2 紫外敏感器测量精度对导航精度的影响Table 2 Influence of measurement accuracy of ultraviolet sensor on navigation accuracy
(2) 采样周期对导航精度的影响
分别取采样周期0.1,1,10,100 s,研究采样周期对导航精度的影响。取初始位置误差500 m,初始速度误差0.05 m/s,紫外敏感器精度0.01°(1δ),仿真结果见表3。可知,采样周期越短导航精度越高。实际工程中采样周期的选取要综合考虑导航精度、系统可观测性、成像曝光时间以及数据处理速度的要求[15]。
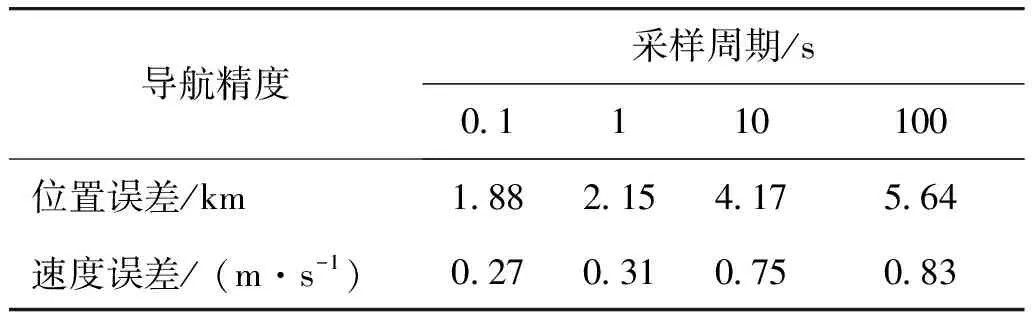
表3 采样周期对导航精度的影响Table 3 Influence of sampling period on navigation accuracy
3.3可观测性分析
如果系统的状态能被过去的观测值唯一确定,则该系统为可观测的[2]。基于紫外敏感器的自主导航其状态方程和观测方程均为非线性的,因此本文将非线性系统线性化、将时变系统等效为分段线性定常系统,结合扩展卡尔曼滤波的特点,对系统可观测性进行分析。
可观测性矩阵定义为[16-17]

图4 仿真结果图Fig.4 Simulation results chart
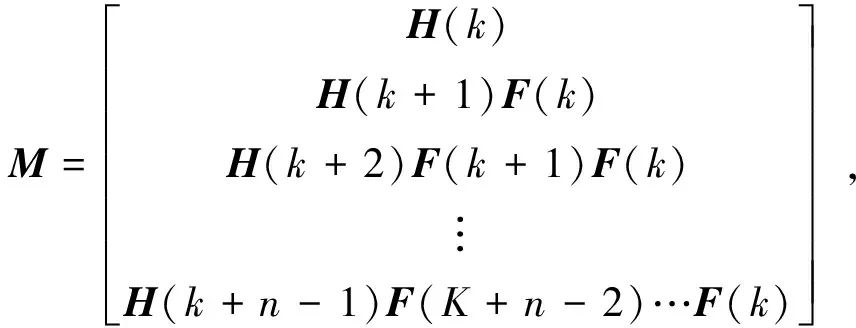
(9)
若rand(M)=6,则系统可观测。同时取系统可观测性矩阵M的条件数cond(M)作为系统可观测度的度量标准。如果可观测性矩阵的条件数较大,说明该可观性矩阵为一个病态矩阵,可观度就较差,在相同量测误差下得到的估计误差就较大;反之,可观性矩阵的条件数较小,则可观度较好。
系统的可观测性一般受到在轨参数、采样周期以及观测量选取的影响。分别取采样周期0.1,1,10,100 s,研究采样周期对系统可观测性的影响。取初始位置误差10 km,初始速度误差2 m/s,紫外敏感器精度0.01°(1δ),在点( 6.509 244 371 304 875e+006,0,3.713 244 835 519 765e+006)处进行分析,仿真结果见表4。显然系统可观,随着采样周期的增长,可观性矩阵的条件数随之增大,系统可观度降低。对应图5~8,可知可观度越好收敛速度越快。实际工程中采样周期的选取要综合考虑导航精度、系统可观测性、成像曝光时间以及数据处理速度的要求。
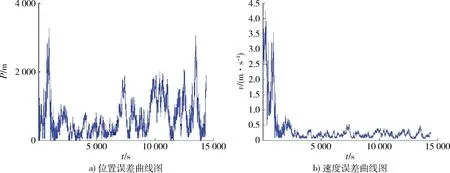
图5 不同采样周期收敛速度(T=0.1 s)Fig.5 Convergence rate of different sampling periods(T=0.1 s)

图6 不同采样周期收敛速度(T=1 s)Fig.6 Convergence rate of different sampling periods(T=1 s)

图7 不同采样周期收敛速度(T=10 s)Fig.7 Convergence rate of different sampling periods(T=10 s)

图8 不同采样周期收敛速度(T=100 s)Fig.8 Convergence rate of different sampling periods(T=100 s)
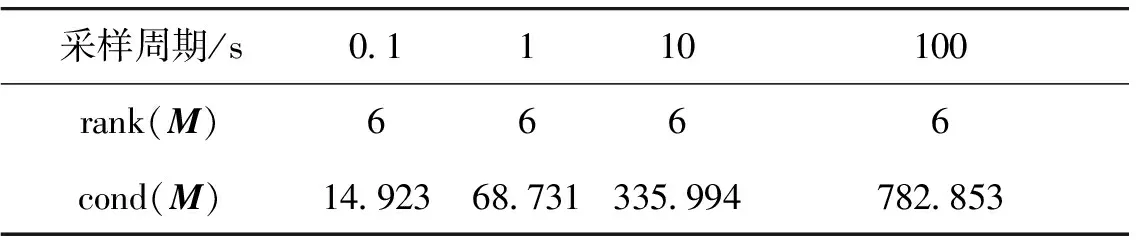
表4 采样周期对系统可观测性的影响Table 4 Influence of sampling period on the observability of the system
4 结束语
本文针对中高轨轨道转移航天器设计了一种基于紫外敏感器的自主导航方案。紫外敏感器采用中心视场和环形视场同轴的结构,用中心视场观测地球,将地球视为质点仅以地心方向矢量作为观测量,EKF滤波算法估计出航天器的位置和速度。此方案同时解决了紫外敏感器应用于中高轨航天器不全程可见和地心距测量误差大的问题。并以从轨道高度1 000 km转移到轨道高度36 000 km为例进行仿真,仿真结果表明:
(1) 紫外敏感器测量精度0.01°(1δ),飞行4h最终位置误差1.23 km,速度误差0.17 m/s,方案有效;
(2) 该方案对初始误差不敏感;
(3) 紫外敏感器测量精度越高导航精度越高,且地心方向测量误差不大于0.05°时导航精度位置误差不超过4 km、速度误差不超过0.5 m/s,该方案有效可行,具有工程价值和实际意义;
(4) 采样周期越短导航精度越高,系统可观性越好,滤波收敛速度越快。实际工程中采样周期的选取要综合考虑导航精度、系统可观测性、成像曝光时间以及数据处理速度的要求。
[1] 管乐鑫,魏春岭.基于紫外敏感器和星敏感器的卫星自主导航[J].空间技术与应用,2008,34(3):37-41.
GUAN Yue-xin ,WEI Chun-ling.Satellite Autonomous Navigation Based on UV Sensor and Star Sensor[J].Space Technology and Application,2008,34(3):37-41.
[2] 房建成,宁晓琳,田玉龙.航天器自主天文导航原理与方法[M].北京:国防工业出版社,2006:2-3.
FANG Jian-cheng,NING Xiao-lin,TIAN Yu-long.Principle and Method of Autonomous Celestial Navigation for Spacecraft[M].Beijing:National Defence Industry Press,2006:2-3.
[3] 耿建中,肖业伦,韩潮.基于紫外敏感器的卫星自主导航方法研究[J].航天控制,2007,25(2):47-51.
GENG Jian-zhong,XIAO Ye-lun,HAN Chao.Satellite Autonomous Navigation Based on UV Sensor[J].Aerospace Control ,2007,25(2):47-51.
[4] PLEDGER D,BILLING-ROSS J,SAYLOR W.Development of Honeywells Earth Refrence Attitude Determination System(ERADS)[R].Proc.of the 7th Annual AIAA/USU Conf.On Small Stallites,1993.
[5] 乔国栋,李铁寿,王大秩.基于紫外敏感器的地月转移轨道慢旋探测器的自主导航算法[J].宇航学报,2009,30(2):1-15.
QIAO Guo-dong,LI Tie-shou,WANG Da-zhi.Autonomous Navigation Algorithm Based on UV Sensor for the Slow Rotation of the Earth Moon Transfer Orbit[J].Acta Astronautica,2009,30(2):1-15.
[6] 宋琛,张蓬蓬,张剑波.基于紫外敏感器的卫星导航[J].计算机仿真,2010,27(11):14-15.
SONG Chen,ZHANG Peng-peng,ZHANG Jian-bo.Satellite Navigation Based on UV Sensor[J].Computer Simulation,2010,27(11):14-15.
[7] 魏春铃,李勇,陈义庆.基于紫外敏感器的航天器自主导航[J].航天控制,2004,22(3):35-39.
WEI Chun-ling,LI Yong,CHEN Yi-qing.Spacecraft Autonomous Navigation Based on UV Sensor[J].Aerospace Control,2004,22(3):35-39.
[8] 马元申,陈文清,张文静.空间战总体概念体系结构分析[J].航天电子对抗,2003(5):5-8.
MA Yuan-shen,CHEN Wen-qing,ZHANG Wen-jing.Analysis of the System Structure of the Overall Concept of Space War[J].Space Electronic Countermeasure,2003(5):5-8.
[9] 何炬.国外天文导航技术发展综述[J].舰船科学技术,2005,27(5):91-96.
HE Ju.Survey on the Development of Astronomy Navigation Technology Abroad[J].Ship Science and Technology,2005,27(5):91-96.
[10] 施常勇,贺亮,夏永江.基于多目标紫外敏感器的自主导航技术[C]∥上海市红外与遥感学会2008年学术年会会议论文,2008.
SHI Chang-yong,HE Liang,XIA Yong-jiang.Autonomous Navigation Technology Based on Multi Objective UV Sensor[C]∥Proceedings of the 2008 Annual Conference of the Society of Infrared and Remote Sensing,Shanghai,2008.
[11] 郝云彩,王立.紫外月球敏感器的几个关键问题[J].航天控制,2005,23(1):87-91.
HAO Yun-cai,WANG Li.Some Key Problems of the Ultraviolet Lunar Sensor[J].Aerospace Control,2005,23(1):87- 91.
[12] Al Lemay J L.High Altitude Navigation Study[R].El Segundo,1973.
[13] BRUNKE S S.Nonlinear Filtering and Systems Identification Algorithms for Autonomous System[D].PhD Thesis:University of Washington,2001.
[14] FESQ L.Spacecraft Autonomy in the New Millennium.Proc.of the Annual AAS Rocky Mountain[C]∥Guidance and Control Conference,Breckenridge,Colorado,1996,AAS 96- 001.
[15] WERTZ J R.Autonomous Navigation Systems.In:Mission Geometry:Orbit and Constellation Design and Management.El Segundo[J].CA:Microcosm Press,2001,17(2):210-218.
[16] 王鹏.基于星载敏感器的卫星自主导航及姿态确定方法研究[D].哈尔滨:哈尔滨工业大学,2008.
WANG Peng.Research on Satellite Autonomous Navigation and Attitude Determination Based on Star Sensor[D].Harbin:Harbin Institute of Technology,2008.
[17] 胡小平.自主导航理论与应用[M].长沙:国防科学技术大学出版社,2002:42-73.
HU Xiao-ping.Autonomous Navigation Theory and Application[M].Changsha:National Defense Science and Technology University Press,2002:42-73.
ApplicationofUltravioletAutonomousNavigationforOrbitTransferSpacecraft
PAN Jing,YAO Hong-ying
(The Second Academy of CASIC,706 Institute,Beijing 100854,China)
To improve the performance of ultraviolet sensor applied to middle and high orbit transfer spacecraft, an autonomous navigation scheme based on ultraviolet sensor is proposed. By observing the ultraviolet image of earth with sensors, geocentric vector information is provided and then the orbit of the spacecraft can be determined. The scheme is designed without range measurements, since range error to earth is too huge to use during orbit transfer from height 1 000 km to 36 000 km. The algorithmic model is established, and simulation is taken using extended Kalman filter with orbit data and measurement data. Apart from the influence of sensor measurement precision, sampling period on the navigation accuracy is studied, and observability properties are investigated. The simulation results show that the scheme is effective and the navigation filter can also converge to acceptable accuracy.
autonomous navigation;ultraviolet sensor;orbit transfer;geocentric vector;dimensionality reduction;extended Kalman filter (EKF)
2016-12-14;
2017-02-20
有
潘静(1990-),女,北京人。助工,学士,主要研究方向为控制科学与工程。
通信地址:100854 北京142信箱406分箱一室E-mail:panjing_6776@126.com
10.3969/j.issn.1009-086x.2017.05.011
V448.22+4;TP391.9
A
1009-086X(2017)-05-0063-09
