EKF在SINS/GNSS深组合导航中的应用*
2017-11-20连文浩杨小龙朱磊程帅
连文浩,杨小龙,朱磊,程帅
(中国人民解放军63981部队,湖北 武汉 430311)
☞导航、制导与控制
EKF在SINS/GNSS深组合导航中的应用*
连文浩,杨小龙,朱磊,程帅
(中国人民解放军63981部队,湖北 武汉 430311)
为了在卫星较少条件下也能提供连续稳定、精度高的导航,建立了一种基于扩展卡尔曼滤波器(extended Kalman filter,EKF)的捷联惯导系统(strapdown inertial navigation system,SINS)/全球导航卫星系统(global navigation satellite system,GNSS)深组合导航系统,并对该系统所采用的导航结构、状态估计算法等进行研究设计。最后,在战术级条件下,分别对单独的SINS,SINS/GNSS松组合导航系统和SINS/GNSS深组合导航系统进行仿真验证,并对导航结果进行对比分析。从仿真结果可以看出,深组合导航系统位置误差约为0.3 m,速度误差约为0.01 m/s,姿态误差约为0.005°。对比分析可知深组合导航精度更高,且不受卫星个数条件影响,具有很高的实用价值。
SINS/GNSS深组合导航;扩展卡尔曼滤波;状态估计;导航精度;导航定位结果;战术级
0 引言
SINS导航误差通过导航方程被不断积分,使其导航精度会随时间下降[1],而GNSS的输出功率很低,噪声误差大,且导航信号容易被遮挡或干扰[2],而将这2种系统结合起来,可以形成连续、高带宽、精度高的组合导航系统[3]。SINS/GNSS组合导航系统是目前应用最为广泛、性能最优、自主性最强的组合导航系统。它主要是利用GNSS提供的长时间高精度的导航输出参数来对SINS进行误差校正,弥补SINS导航误差随时间增大的缺点,同时利用SINS的连续工作能力对GNSS信号中断进行辅助,平滑处理导航结果,提高GNSS的抗干扰能力,从而实现稳定性高、可靠性强、精度高的全天候导航能力[4-5]。
SINS/GNSS组合导航系统导航结果的最优化求解、导航系统的位置和速度误差估计等都要用到卡尔曼滤波(Kalman filter,KF)[6]。标准的卡尔曼滤波算法中,通常假设组合导航系统是线性的,然而实际系统并非如此[7]。本文运用卡尔曼滤波的非线性形式——EKF来对导航系统进行状态估计,有效的解决了组合导航系统观测参数非线性化,时间相关噪声、系统噪声标准方差未知和观测数据非高斯分布等实际问题[8-9]。
1 组合导航结构
SINS/GNSS组合导航系统结构主要包括松组合、紧组合和深组合,本节分别对这3种组合导航结构进行阐述,并就其各自的优缺点进行对比分析。
1.1松组合导航
SINS/GNSS松组合导航是利用GNSS输出的位置和速度参数,作为输入传递给卡尔曼滤波器,后者用它来估计SINS误差,同时,根据SINS误差对SINS导航参数进行校正,校正后的SINS导航参数作为组合导航的输出。SINS/GNSS松组合导航系统结构如图1所示。

图1 松组合导航系统结构Fig.1 Structure of loose integrated navigation system
在SINS/GNSS松组合卡尔曼滤波器中,会假设输入的测量噪声是时间不相关的,这与实际GNSS测距处理器的输出参数是不相符的,这个问题严重影响了卡尔曼滤波器在松组合导航系统中的使用。而且,松组合导航系统至少需要4颗导航卫星,才能保证GNSS输出有效的导航参数[10]。因此,松组合导航系统的使用具有限制性。
1.2紧组合导航
紧组合导航是在距离域进行的,扩展卡尔曼滤波器的输入值源于GNSS测距处理器的伪距和伪距率,以此来估计SINS误差和GNSS的钟差。与松组合导航相同,紧组合导航输出结果也是校正后的惯导参数。其具体结构如图2所示。

图2 紧组合导航系统结构Fig.2 Structure of tight integrated navigation system
从图2中可以看出,紧组合导航系统将GNSS测距处理器和SINS/GNSS组合算法合并成一个算法,这就解决了松组合导航中假设卡尔曼滤波器的噪声时间不相关与实际输出参数不相符的问题。与此同时,当没有足够的导航卫星时,GNSS输出的导航参数也能用于辅助SINS[11]。但是,由于不是所有的GNSS测距处理器都能输出滤波器所需要的距离域参数,因此,容易导致输出参数权值下降和降低卡尔曼滤波器增益等问题。
1.3深组合导航
在深组合导航中,卫星位置和速度,以及GNSS误差估计作为校正后的惯导参数。GNSS接收机累加输出IS和QS,通过预滤波器传输给组合滤波器,组合滤波器估计SINS和GNSS误差,并对SINS参数进行校正,作为组合导航输出结果。深组合导航系统结构如图3所示[12]。
与松组合和GNSS矢量跟踪相比,深组合导航系统只需要跟踪SINS参数误差,而不需要跟踪整个运动轨迹,因此,它能够采用低跟踪带宽,从而增强系统的抗噪声能力。并且深组合导航系统还可以在少于4颗导航卫星的情况下工作。
与紧组合相比,深组合导航系统在滤波器中去除了跟踪环路滤波和级联滤波,避免了输出参数权值下降和卡尔曼滤波器增益降低等问题。通过改变输出参数权值,可以适用于不同的C/N0水平,当导航卫星信号中断时,深组合导航系统也可以利用闭合码和载波频率跟踪。因此,深组合导航系统结构是最优的组合结构。
2 状态估计
组合导航系统的状态估计算法决定了系统的导航参数,而卡尔曼滤波则是导航系统中绝大部分状态估计的基础算法,被广泛应用于GNSS和陆基无线电导航、GNSS信号检测、组合导航、SINS的精确对准和标校等。
2.1卡尔曼滤波
卡尔曼滤波不仅是一种滤波器,更是一类状态估计算法。它包含5个核心要素:系统模型、状态向量及其协方差、观测模型、观测向量及其协方差和滤波算法。
2.1.1 系统模型
卡尔曼滤波要求所有状态的时间导数是其他状态和白噪声的线性函数。在t时刻卡尔曼滤波的状态向量x(t)可以表示为[13]

(1)
式中:ω(t)为系统噪声向量;F(t)为系统矩阵;G(t)为连续系统噪声分布矩阵。
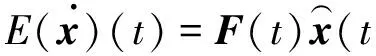
(2)
当F(t)在(t-τs)~t之间时,F(t)可近似为常数,由式(2)可得

(3)
在离散卡尔曼滤波中,状态估计值是前一时刻估计值的线性函数,可以表示为
(4)
式中:Φk-1为状态转移矩阵。
将式(3)带入式(4)得
Φk-1≈exp(Fk-1τs).
(5)

图3 深组合导航系统结构Fig.3 Structure of deep integrated navigation system
当F(t)和G(t)在积分时间间隔内近似为常数时,由式(5)可得
xk=Φk-1xk-1+Γk-1ωk-1,
(6)
式中:ωk-1为离散系统的噪声向量;Γk-1为离散系统噪声分布矩阵。
假设系统噪声为白噪声,可以得到系统噪声协方差矩阵为
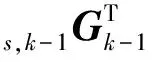
(7)
2.1.2 观测模型
在t时刻卡尔曼滤波的观测向量可以表示为
z(t)=H(t)x(t)+υ(t),
(8)
式中:H(t)为观测矩阵;υ(t)为白噪声源。
状态估计值是观测值与前一时刻的估计值的线性组合,可以表示为
(9)
式中:Kk和Lk为权值函数。
状态估计误差和观测噪声是不相关的,因此由式(9)可以得到误差协方差矩阵为
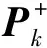
(10)
2.2扩展卡尔曼滤波(EKF)
卡尔曼滤波算法的推导是建立在对被估状态和噪声源特性的假设上的,这在实际导航系统中并不一定成立,因此,需要EKF算法,以此来解决非线性系统模型、时间相关噪声、系统/观测噪声方差未知等问题[14]。
EKF是卡尔曼滤波的非线性化形式,它的系统动态模型可以表示为

(11)
根据2.1节内容可以得到状态向量传播公式为
(12)
由于在EKF中,假设状态向量估计的误差远小于状态向量,因此系统状态向量残差可以表示为

(13)
EKF的观测模型为
z(t)=h(x(t),t)+υ(t),
(14)
式中:h为状态向量的非线性函数。
由式(14)可以得到观测新息为
(15)
2.3基于滤波的导航定位解算
导航定位解由卡尔曼滤波器的状态向量组成,无论载体是否移动,导航解的位置和速度都是被估计的。在导航滤波器的系统模型和观测模型中,存在8个待估的状态量:天线位置、速度、接收机钟差和接收机时钟漂移。
在不同坐标系下,导航滤波器的状态向量分别表示为
(16)
(17)
式中:上标i为地心惯性坐标系(ECI)坐标系;e为地心地固坐标系(ECEF)坐标系。
结合2.1节和2.2节内容,系统噪声协方差矩阵可以表示为
(18)

由于在GNSS导航模型中,伪距和伪距率是状态估计值的非线性函数,因此,必须使用EKF测量模型。同样由2.1节和2.2节内容可知,在ECI系和ECEF系中,预测的伪距测量矩阵可以表示为
(19)
式中:j表示卫星s和卫星信号的总称;W表示三维坐标系;ρ表示伪距;v表示速度;γ表示ECI系和ECEF系。
3 基于EKF的组合导航系统模型
在SINS/GNSS组合导航系统中,GNSS导航处理器测量输出值与根据SINS参数预测的测量值之间的差被用作更新状态向量,因此,由SINS和GNSS得到的测量值必须是同时有效的。
3.1基于EKF的松组合导航系统
SINS/GNSS松组合导航系统所输出的导航解要运用到GNSS导航设备的位置和速度参数,因此,它的测量新息向量包括GNSS参数和校正后的SINS位置和速度参数的差值,同时也对SINS到GNSS天线的传输路径进行了补偿[15]。根据第2章内容可知,基于EKF的SINS/GNSS松组合导航系统测量矩阵可以表示为
(20)
在某些特定情况下,姿态误差和陀螺零偏在导航过程中是弱耦合的,这些误差主要通过速度误差的变化进行估计,因此,测量矩阵中的非常数项可近似为0,在此不多加讨论。
3.2相干预滤波器深组合导航
相干预滤波器的核心部件是估计码相位、载波相位和载波频率跟踪误差的跟踪滤波器,通常采用的是EKF算法。SINS/GNSS深组合的相干预滤波器的工作原理如图4所示[16-17]。
为了使载波相位估计精确,跟踪滤波器的更新频率至少应为50 Hz,因此,只有在接收机的输出频率很高时,才能进行Is和Qs相关求和。同时,在进行伪距和伪距率测量时,输出到组合滤波器的频率通常为1 Hz或2 Hz。
所有的相干滤波器都要估计码跟踪误差、载波相位误差和载波频率误差,还可以根据实际情况估计载波频率跟踪误差的导数和载波功率噪声密度比。如果估计载波频率跟踪误差的导数,则状态估计的系统模型可以表示为
(21)
由于存在接收机时钟噪声,频率跟踪误差必须建立相应的噪声方差,噪声方差与实际方向的加速度和的平方成正比。
如果导航接收机前段有自动增益控制(AGC),那么测量噪声就是一个常数(信号幅度随c/n0变化)。噪声标准差根据接收机设计的不同而变化,此时,滤波器的伪距测量新息可以表示为
(22)
因此,根据式(19)和式(22)可以得到,深组合导航测量矩阵可以表示为
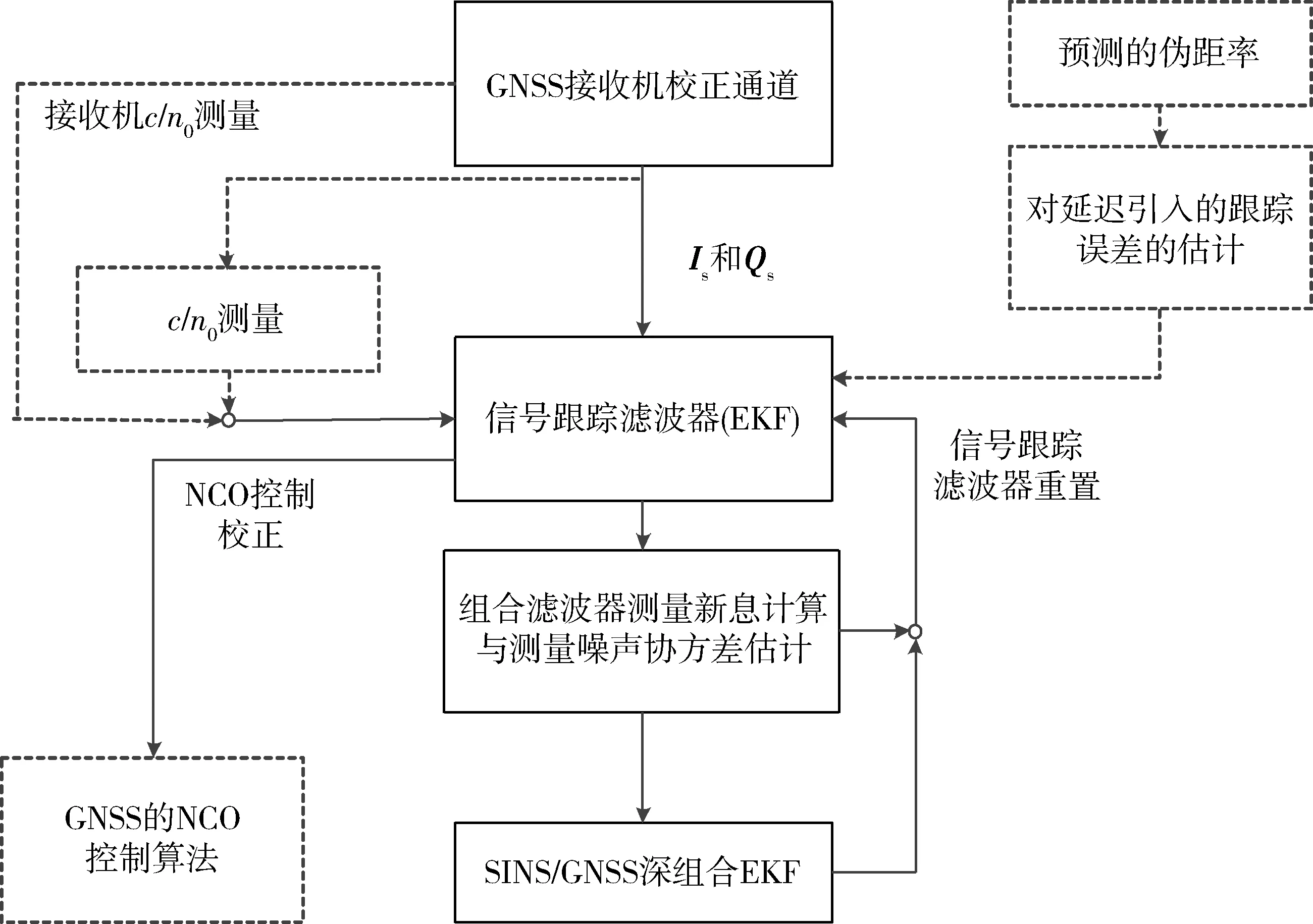
图4 深组合的相干预滤波器Fig.4 Phase interference filter of deep combination
(23)
式中:ψ为偏航角或方位角。
在SINS/GNSS深组合导航中,导航接收机接收的NCO控制命令是惯导处理器产生的,因此,产生NCO命令的有效时间和接收命令的有效时间之间存在明显的延时,影响延时的因素主要有:IMU采样窗口的长度;从IMU采样输出到惯导处理器、惯性导航参数计算、生成NCO命令所花费的时间;与导航接收机进行NCO命令通信、应用NCO命令花费的时间;GNSS相关窗口长度等[3]。
对于大多数的导航处理器,如果做了延迟补偿,那么以50 Hz来更新NCOC命令就足够了。如果没有延迟补偿,则更新频率应调整为100 Hz。
4 仿真验证及对比分析
采用Spirent SinGen软件仿真出的车载运动轨迹作为战术级SINS,SINS/GNSS松组合导航系统和SINS/GNSS深组合导航系统的Matlab仿真输入。
4.1战术级SINS仿真
仿真条件为:惯性导航系统,战术级惯导器件,ECEF坐标系下,载车初始速度20 m/s,90°转弯,加速到20 m/s,-90°转弯,再加速到20 m/s,运动一段距离后停车。其导航仿真位置误差如图5所示,速度误差如图6所示,姿态角误差如图7所示。
从图5~7中可以看出,单独的SINS导航误差随仿真时间加长而不断变大,呈积分趋势。

图5 战术级SINS导航位置误差Fig.5 Position error of SINS in tactical level

图6 战术级SINS导航速度误差Fig.6 Velocity error of SINS in tactical level

图7 战术级SINS导航姿态角误差Fig.7 Attitude angle error of SINS in tactical level

图8 SINS/GNSS松组合导航位置误差Fig.8 Position error of loose integrated navigation system of SINS/GNSS
4.2SINS/GNSS松组合导航系统仿真
仿真条件为:SINS/GNSS松组合导航系统,战术级惯导器件,ECEF坐标系下,GNSS导航卫星4颗,卫星信号预相关带宽50 MHz,接收机通道数12,组合滤波器测量更新频率1Hz,载车初始速度20 m/s,90°转弯,加速到20 m/s,-90°转弯,再加速到20 m/s,运动一段距离后停车。其导航仿真位置误差如图8所示,速度误差如图9所示,姿态角误差如图10所示。
从图8~10中可以看出,与单独的SINS相比,SINS/GNSS松组合导航误差整体呈收敛趋势,但在某些时间点,导航误差会出现跳变,这是受导航卫星数影响的结果。
4.3SINS/GNSS深组合导航系统仿真
仿真条件为:SINS/GNSS深组合导航系统,战术级惯导器件,ECEF坐标系下,GNSS导航卫星3颗,卫星信号预相关带宽50 MHz,接收机通道数12,组合滤波器测量更新频率50 Hz,载车初始速度20 m/s,90°转弯,加速到20 m/s,-90°转弯,再加速到20 m/s,运动一段距离后停车。其导航仿真位置误差如图11所示,速度误差如图12所示,姿态角误差如图13所示。
从图11~13中可以看出,与SINS/GNSS松组合导航类似,SINS/GNSS深组合导航误差也呈收敛趋势,但其误差曲线变化较松组合平缓,且基本没有明显跳变。
4.4仿真结果对比
分别选取仿真60 s时单独的惯导、SINS/GNSS松组合导航、SINS/GNSS深组合导航的位置误差、速度误差和姿态角误差进行对比分析,其具体误差数据如表1所示。

表1 导航误差数据Table 1 Navigation error data

图9 SINS/GNSS松组合导航速度误差Fig.9 Velocity error of loose integrated navigation system of SINS/GNSS

图10 SINS/GNSS松组合导航姿态角误差Fig.10 Attitude angle error of loose integrated navigation system of SINS/GNSS
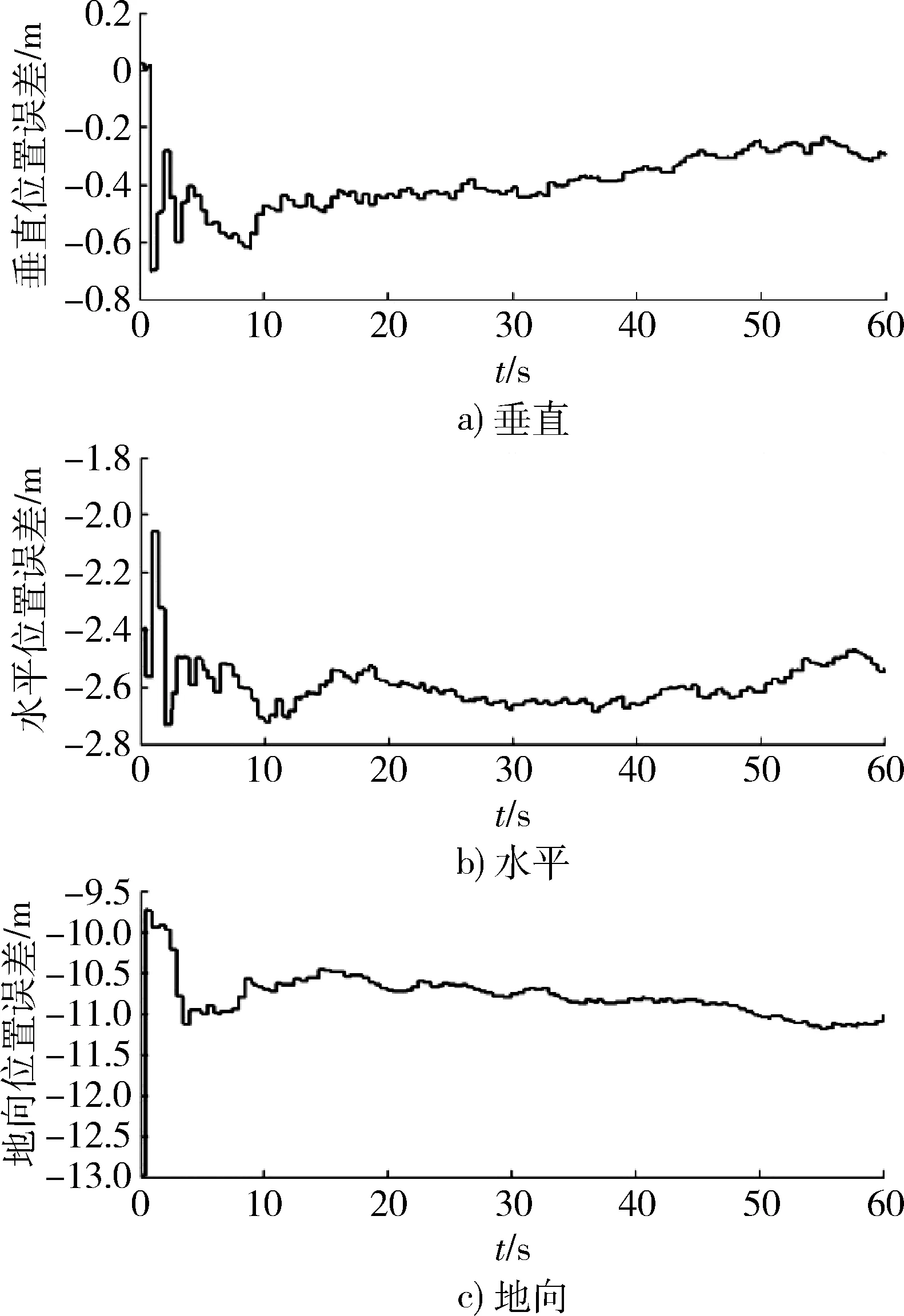
图11 SINS/GNSS深组合导航位置误差Fig.11 Position error of deep integrated navigation system of SINS/GNSS
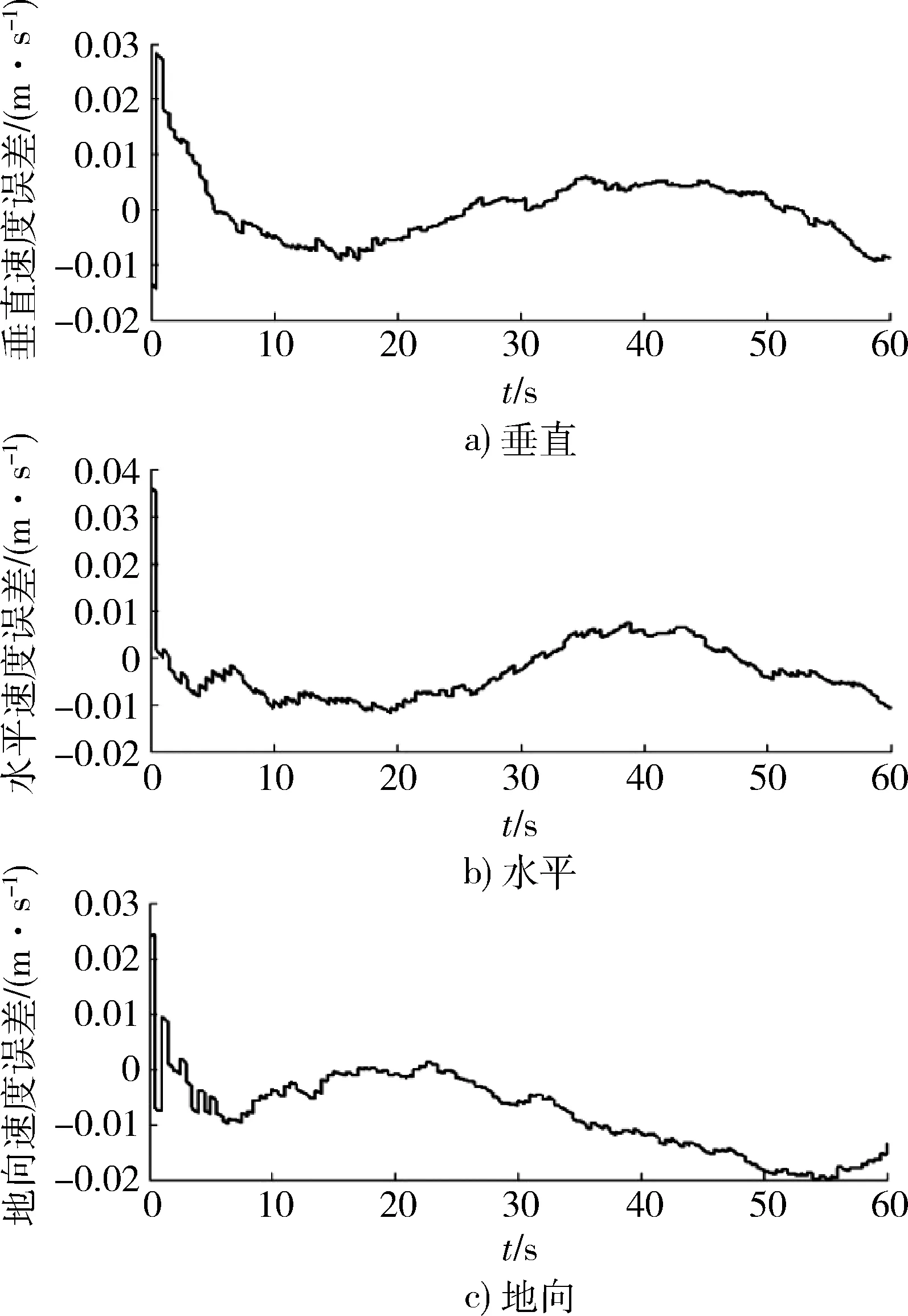
图12 SINS/GNSS深组合导航速度误差Fig.12 Velocity error of deep integrated navigation system of SINS/GNSS

图13 SINS/GNSS深组合导航姿态角误差Fig.13 Attitude angle error of deep integrated navigation system of SINS/GNSS
5 结论
本文建立基于EKF的SINS/GNSS深组合导航定位模型,通过仿真验证得到导航误差结果,并与单独的SINS以及SINS/GNSS松组合导航误差结果进行对比分析,主要结论如下:
(1) 与单独的SINS相比,SINS/GNSS深组合导航系统导航误差明显下降,且通过GNSS导航参数对SINS进行初始化校正,可以避免SINS导航误差的积分趋势。
(2) 与SINS/GNSS松组合导航相比,SINS/GNSS深组合导航位置误差基本稳定,速度误差也基本在同一数量级,姿态角误差明显降低1~2个数量级。
(3) 从仿真结果可以看出,本文建立的SINS/GNSS深组合导航系统导航结果更加稳定,不会出现明显跳变现象,在相同条件下,其对导航环境的适应能力更强,且不受导航卫星数影响,在少于4颗导航卫星时,仍能稳定输出导航结果,具有较高的实际应用价值。
[1] Paul D Groves.Principles of GNSS,Inertial and Multisensor Intergrated Navigation Systems[M].MA:Artech House,2013.
[2] HEIN G W.Envisioning a Future GNSS System of Systems,Part one[M].NJ:Inside GNSS,2007:58-67.
[3] GROVES P D,MATHER C J.Receiver Interface Requirements for Deep INS/GNSS Integration and Vector Tracking[J].Journal of Navigation,2010,63(3):471-489.
[4] 崔留争,高思远,贾宏光,等.神经网络辅助卡尔曼滤波在组合导航中的应用[J].光学精密工程,2014,22(5):1304-1311.
CUI Liu-zheng,GAO Si-yuan,JIA Hong-guang,et al.Application of Neural Network Aided Kalman Filtering to SINS/GPS[J].Optics and Precision Engineering,2014,22(5):1304-1311.
[5] HIROKAWA R,EBINUMA T.A Low-Cost Tightly Coupled GPS/INS for Small UAVs Augemented with Multiple GPS Antennas[J].Navigation:JION,2009,56(1):35-44.
[6] 王坚,刘超,高井祥,等.基于抗差EKF的GNSS/INS紧组合算法研究[J].武汉大学学报:信息科学版,2011,35(5):596-600.
WANG Jian,LIU Chao,GAO Jing-xiang,et al.GNSS/INS Tightly Coupled Navigation Model Based on Robust EKF[J].Journal of Wuhan University:Geomatics and Information Science ed,2011,35(5):596-600.
[7] XING Z,Gebre Egziabher D.Comparing Non-Linear Filters for Aided Inertial Navigators[C]∥ION ITM,Anaheim,2009:1048-1053.
[8] DRAGANOV A,HAAS L,HARLACHER M.The IMRE Kalman Filter-a New Kalman Filter Extension for Nonlinear Applications[C]∥IEEE/ION PLANS,Myrtle Beach,2012:428-440.
[9] 魏彤,郭蕊.自适应卡尔曼滤波在无刷直流电机系统参数辨识中的应用[J].光学精密工程,2012,20(10):2308-2314.
WEI Tong,GUO Rui.Application of Adaptive Kalman Filter to System Identification of Brushless DC Motor[J].Optics and Precision Engineering,2012,20(10):2308-2314.
[10] KIESEL S.Discriminator Weighting and Performance of Deeply Coupled GPS/INS System at Low C-No[C]∥ION ITM,San Diego,2011:858-867.
[11] WANG X L,LI Y F.An Innovative Scheme for SINS/GPS Ultra-Tight Integration System with Low-Grade IMU[J].Aerospace Science and Technology,2012,23(1):452-460.
[12] SIVANANTHAN S,WEITZEN J.Improving Optimality of Deeply Coupled Integration of GPS and INS[C]∥ION ITM,Anaheim,2009:426-433.
[13] SIMON D.Optimal State Estimation[M].New York:Wiley,2006.
[14] 韩辅君,徐静,宋世忠.基于低成本多传感器的自适应组合滤波[J].光学精密工程,2011,19(12):3007-3015.
HAN Fu-jun,XU Jing,SONG Shi-zhong.Adaptive Attitude Estimation Filtering with Low-Cost Multi-Sensors for MAHRS[J].Optics and Precision Engineering,2011,19(12):3007-3015.
[15] SENNOTT J W,SENFFNER D.Navigation Receiver with Coupled Signal-Tracking Cbannels[R].U.S.Patent 5343209,1994.
[16] ABBOTT A S,LILLO W E.Global Positioning System and Intertial Measuring Unit Ultratight Coupling Method[R].U.S.Patent 6516021,2003.
[17] Beser J Trunav.A Low-cost Guidance/Navigation Unit Integrating a SAASM-Based GPS and MEMS IMU in a Deeply Coupled Mechanization[C]∥ION GPS 2002,Portland OR,2002:545-555.
EKFUsinginDeepIntegratedNavigationSystemofSINS/GNSS
LIAN Wen-hao,YANG Xiao-long,ZHU Lei,CHENG Shuai
(PLA,No.63981 Troop,Hubei Wuhan 430311,China)
A deep integrated navigation system of SINS/GNSS is established based on EKF to provide continuous and stable, high precision navigation on the condition of less satellites. At the same time, the navigation structure and state estimation algorithm of this system are studied. Finally, the navigation results of individual SINS, loose integrated navigation system of SINS/GNSS and deep integrated navigation system of SINS/GNSS are verified by simulation at tactical level. The simulation results show that the position error of deep integrated navigation system is about 0.3 m, velocity error is about 0.01 m/s, attitude angle error is about 0.005°. It indicates that the precision of deep integrated navigation is higher, which is not affected by satellite condition, and has very high practical value.
deep integrated navigation system of SINS/GNSS;extended Kalman filter(EKF);state estimation;navigation accuracy;navigation positioning result;tactical level
2016-09-18;
2016-12-30
有
连文浩(1987-),男,山东荣成人。助工,硕士,主要从事导航、雷达技术等方面研究。
通信地址:430311 湖北省武汉市黄陂区汉口北大道195号E-mail:546425830@qq.com
10.3969/j.issn.1009-086x.2017.05.010
V249.32+2;TN967.1
A
1009-086X(2017)-05-0053-10
