基于声发射的铝蜂窝板超高速撞击损伤模式识别方法

刘源， 庞宝君， 迟润强， 才源

哈尔滨工业大学 航天学院， 哈尔滨 150080

基于声发射的铝蜂窝板超高速撞击损伤模式识别方法

刘源， 庞宝君， 迟润强*， 才源

哈尔滨工业大学 航天学院， 哈尔滨 150080

为通过声发射技术识别铝合金蜂窝板超高速撞击(HVI)的损伤状态，提出一种基于神经网络的损伤模式识别方法。通过超高速撞击实验获取声发射信号，结合精确源定位技术、时频分析技术、小波分析技术及模态声发射技术，提出了10个与损伤相关的特征参数，通过非参数检验分析其与损伤的关系，设计了一种基于贝叶斯正则化BP神经网络的超高速撞击损伤模式识别方法。建立最优网络模型，通过不同参数组合识别能力分析，优选出2种特征参数组合，通过非同源样本对其损伤模式识别能力进行验证。结果表明：传播距离与损伤模式无关，却是识别损伤模式的重要参数；125～250 kHz频域的自动加窗小波能量比会降低损伤模式的识别能力；采用贝叶斯正则化的BP神经网络可以较好地识别蜂窝板超高速撞击损伤模式，参数组合为传播距离、上升时间、持续时间、截止频率、4个自动加窗小波能量比及小波能量熵，共9个参数，对任意选取非同源样本识别错分率仅为9.38%。

空间碎片； 超高速撞击； 声发射； 损伤模式识别； 神经网络

空间碎片对航天器在轨安全运行构成严重威胁[1]，其中毫米级空间碎片的准确运行轨道难以观测，无法进行有效规避，具有较大的撞击威胁。为保障航天器的在轨安全，人们提出一种能够实现对空间碎片超高速撞击(HVI)事件进行感知的系统，称为“在轨感知系统”，主要具有感知撞击事件发生、定位撞击源及撞击损伤模式识别等能力，其中损伤模式识别是目前研究的重点和难点。基于声发射技术的在轨感知系统具有较好的可实现性及较高的定位能力，美国国家航空航天局(NASA)和欧洲空间局(ESA)等机构已开发了 LAD -C (Large Area Debris Collector)、DIDS (Distributed Impact Detector System)、MDD (Micrometeoroid/space Debris Detector)、冲击传感网络(Impact Sensor Network)、DEBIE (DEBris In-orbit Evaluator)等[2-6]基于声发射技术的在轨感知系统；国内也针对多种典型航天器结构受空间碎片超高速撞击在轨感知技术进行研究[7-8]，开发了多种超高速撞击源定位技术[9-11]，并针对平板结构初步提出了超高速撞击损伤模式识别方法[12-13]。

蜂窝板主要由双层蒙皮和蜂窝芯构成，特点是质量轻、比强度和比刚度高、隔热性能好，常用在卫星结构中。目前研究人员对蜂窝板的超高速撞击极限特性进行了研究[14-15]，但针对蜂窝板超高速撞击声发射信号特性研究较少。

超高速撞击导致材料中产生弹、塑性形变及相变等物理过程，形成的超高速撞击声发射信号包含信息复杂，难以通过个别参数建立与损伤的对应关系，尤其是蜂窝板的各向异性性，进一步增加了其受超高速撞击损伤模式识别的难度。本文通过超高速撞击实验，获得蜂窝板在不同损伤程度时的超高速撞击声发射信号，采用多种时频分析手段获得信号的特征参数，设计和优选与损伤相关的特征参数组合，建立针对蜂窝板超高速撞击声发射信号的BP神经网络损伤模式识别模型，并通过非同源样本对模型进行验证。

1 超高速撞击实验

利用二级轻气炮发射∅3.2 mm的2017铝合金球形弹丸撞击实验蜂窝板，通过在实验板面上安装传感器获取信号。

实验蜂窝板的面板尺寸为600 mm×600 mm。前后蒙皮面板的厚度为0.8 mm，铝蜂窝芯的高度为20 mm，由边长为4 mm的正六边形构成，蜂窝芯壁厚为0.025 mm，蒙皮面板及蜂窝芯的材料均为5A06铝合金，结构示意图如图1所示。

将8枚OLYMPUS公司的V182传感器安装在蜂窝板后蒙皮面板上，以板面几何中心为原点，传感器顺时针排列，布局如图2所示。使用多路数据采集系统采集传感器输出的信号，采样频率为20 MHz，采集时间为1 ms。

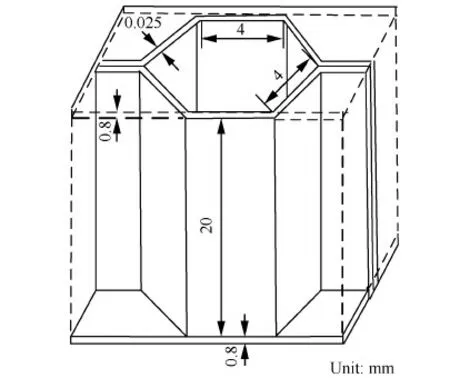
图1 蜂窝板结构示意图 Fig.1 Schematic diagram of honeycomb core sandwich structure

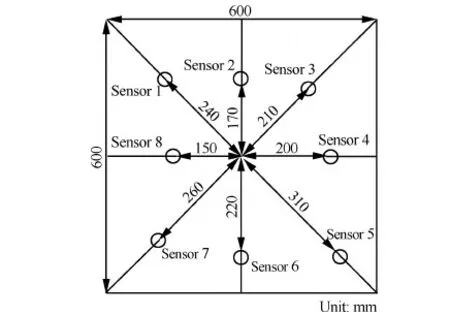
图2 传感器布局图 Fig.2 Sensor installing layout

获得有效信号的实验42次，因此总计包括超高速撞击信号336组。采用磁测速和激光测速测量弹丸撞击的速度，撞击速度及实验编号如表1所示。

根据是否威胁航天器内部组件区分损伤模式。当蜂窝板后蒙皮面板被击穿时，会在航天器内部形成二次碎片，直接威胁内部组件，影响其在轨安全性，因此根据蜂窝板后蒙皮面板的损伤定义2种典型损伤模式：

1) 成坑。蜂窝板后蒙皮面板被撞击损伤后其撞击位置不透光，主要包括背侧未弯曲、背侧弯曲、发生层裂等，在表1中用“0”表示。

2) 穿孔。蜂窝板后蒙皮面板被撞击损伤后撞击位置透光，为了安全起见将临界情况也归入该类，在表1中用“1”表示。

采用AUTODYN数值仿真得到蜂窝板的撞击极限曲线如图3所示，表明在上述损伤定义下，蜂窝板后蒙皮面板产生穿孔损伤时弹丸直径和撞击速度的临界条件，曲线下方工况呈成坑损伤，上方呈穿孔损伤。

通过对实验蜂窝板的观察得到损伤模式，如表1所示，典型的成坑、穿孔损伤工况如图4所示。根据实验共得到成坑损伤10次；穿孔损伤32次，其中包括临界穿孔1次。实验中包括2次实验(2013102806和2013102809)虽超过临界速度，但弹丸在发射过程中破碎，变为2～3枚弹丸碎片撞击实验板，结果仍为成坑损伤，实验工况与图3中的拟合曲线基本吻合。

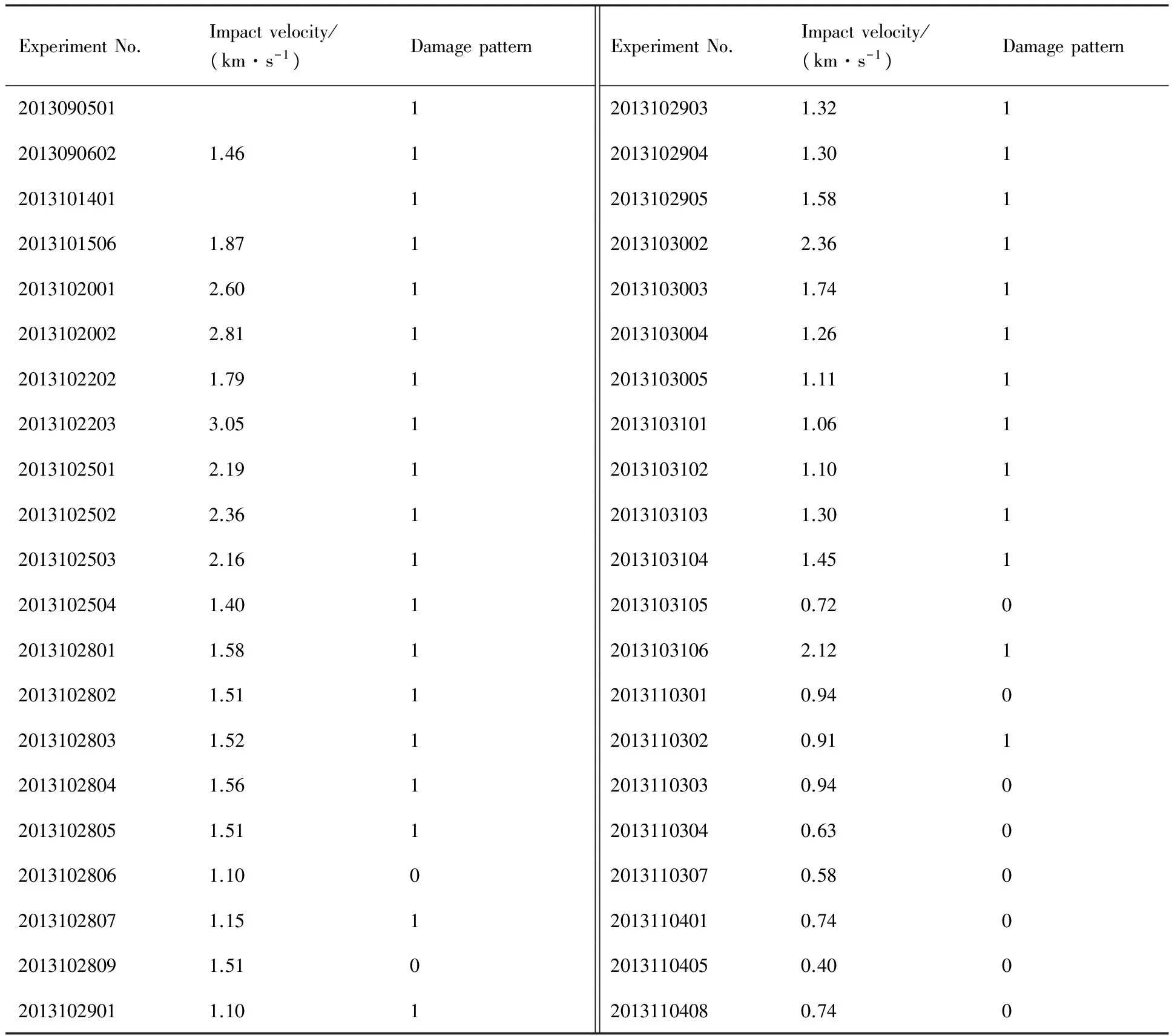
表1 实验工况Table 1 Experiment condition

Notes: 0—Pit damage; 1—Hole damage.

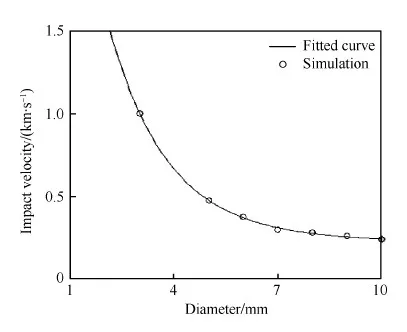
图3 蜂窝板弹道极限曲线 Fig.3 Ballistic limit curve of honeycomb core sandwich

图4 蜂窝板后蒙皮面板超高速撞击损伤情况 Fig.4 Hypervelocity impact damage on back panel of honeycomb core sandwich

2 特征参数提取

2.1 传播距离

传播距离应为信号特征的重要影响因素。因为超高速撞击声发射信号强度在蜂窝板面上是以指数衰减的，衰减的系数与信号频率和传播方向相关[16]。

传播距离为蜂窝板后蒙皮面板形成损伤的位置与传感器的中心位置的距离，通过撞击源定位获得。选择2、5、7号传感器进行3点定位，采用基于虚拟波阵面的精确源定位算法[10]计算撞击的位置，分别针对42次撞击实验进行定位，计算得到平均误差为3.68 mm，最大误差为7.35 mm，全部实验的误差分布如图5所示。

根据板面上板波衰减规律，毫米级别的距离误差远小于信号在板面上的传播距离，因此定位误差对波动中各个频率分量幅值的影响可以忽略不计。

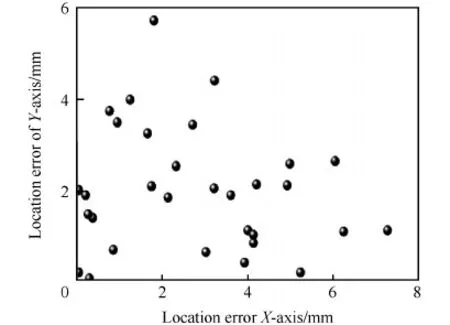
图5 实验定位误差 Fig.5 Location error in experiments

2.2 时域特征参数

声发射信号波形的上升时间和持续时间是声发射检测的重要特征参数。

通过对蜂窝板面上的波速进行测量[16-17]，理论上1 ms内中心位置附近产生的超高速撞击声发射信号可在板面边界发生约2次反射，传感器应采集3次声发射事件，但由于蜂窝板面较薄，信源强度弱，且在蜂窝板面上衰减较快，导致实际采集的信号中仅1次声发射信号清晰可识，蜂窝板面超高速撞击声发射信号波形如图6所示。

由图6可知，该信号是由波速较快的超声部分和波速较慢的非超声部分构成的。非超声部分的传播速度远低于超声部分，当传播距离较远时难以采集其完整的波形，导致该非超声部分信息缺失，通过设计截止频率为20 kHz的高通滤波器，获得超声部分波形，如图7所示。

从滤波后的波形可以识别出，滤波后的波形头部主要由2个波包构成，对应了2个波速不同的模态分量，后端主要由反射信号构成，信号的幅值随时间不断减小。蜂窝板面的撞击声发射信号包含2个板波模态[16]，通过信号中各峰值拟合可知，第1个波包的峰值与后端波形的各峰值近似呈指数关系，这也说明2个波包为两种波速、衰减均不同的模态，其中第1个波包为对称模态，第2个为反对称模态，反对称模态在蜂窝板面上的衰减较快。

基于此，采用上升时间和持续时间作为损伤模式识别的特征参数。

1) 上升时间

信号上升时间：从信号到达到第1个波包的峰值到达所用时间长度。计算信号高通滤波后的包络线如图8所示，可以看到信号由头部的2个波包及后端4个频散波包构成，满足信号在板面上发生2次反射的推测。

采用自动门槛阈值法获取信号的到达时刻。

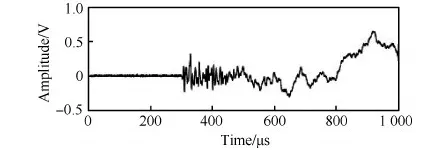
图6 超高速撞击声发射信号 Fig.6 Acoustic emission signal of hypervelocity impact

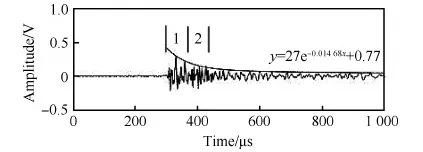
图7 高通滤波后的波形 Fig.7 High-pass filtered waveform

首先，调平高通滤波后的信号，在信号前端选取500个数据点，计算其绝对值的平均值，记为Mt；当信号的绝对值连续5个采样点超过5Mt时，记这个时刻为信号的到达时刻。

蜂窝板后蒙皮面板形成成坑和穿孔等损伤程度与撞击速度呈单调的关系，分析特征参数与撞击速度的关系。336组实验信号的上升时间与撞击速度的关系如图9所示，由图9可知上升时间较为离散，撞击速度小于1 km/s时，上升时间一部分小于50 μs，一部分在150 μs附近；撞击速度大于1 km/s，上升时间多集中于150 μs附近。

2) 持续时间

信号持续时间：前2个波包持续的时间长度，其为信号到达时刻与第2个波包截止时刻的时差，如图10所示。其到达时刻与上升时间的选取方式相同；截止时刻的取法是：在到达时刻后，信号的绝对值第2次出现连续5个采样点低于30Mt的时刻。

336组实验信号的持续时间与撞击速度的关系如图11所示，持续时间与撞击速度的关系比较离散，总体趋势是随着撞击速度上升而增加。

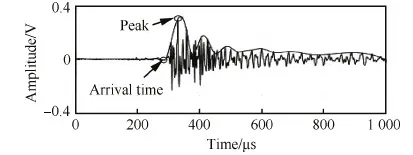
图8 信号上升时间 Fig.8 Rise time of signal

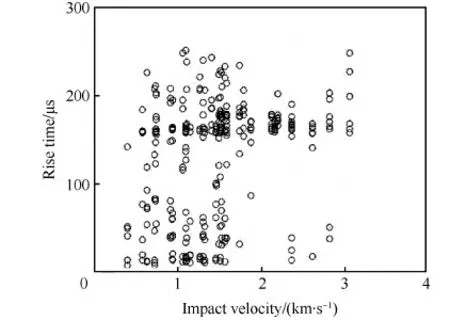
图9 信号上升时间与撞击速度的关系 Fig.9 Relationship between rise time of signal and impact velocity

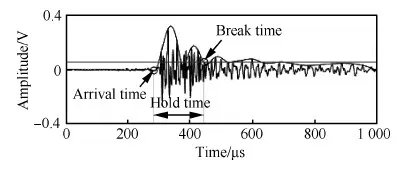
图10 信号持续时间 Fig.10 Hold time of signal

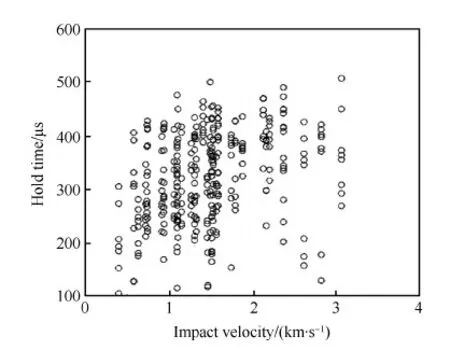
图11 信号持续时间与撞击速度的关系 Fig.11 Relationship between hold time of signal and impact velocity

2.3 频域特征参数

信号的截止频率可作为损伤模式识别的重要特征参数。

虽然超高速撞击声发射信号的中心频率不随撞击速度的变化而改变，但是其截止频率与撞击速度存在一定关系[13]。根据实验可知蜂窝板面上的超高速撞击声发射信号主要在500 kHz以内，两个不同模态的中心频率均在100 kHz附近，因此整体分析信号的频域特征，将信号的截止频率作为特征参数。

超高速撞击声发射信号的频率在低于截止频率范围是始终存在的，尾部的非超声部分能量远大于超声部分，因此截止频率的获取针对滤波后信号，以便于分析。

截止频率的选取采用自动门槛阈值法。首先，对信号进行傅里叶变换，计算信号的频谱，抽取2 MHz以上部分，计算其平均值Mf，以频谱第一次高于5Mf作为起始频率，第一次低于5Mf作为截止频率，信号高通滤波后的截止频率取法如图12所示。

截止频率与撞击速度的关系如图13所示，截止频率与撞击速度在1.5 km/s以下呈单调递增趋势；当撞击速度高于1.5 km/s后，截止频率变化范围趋于稳定。

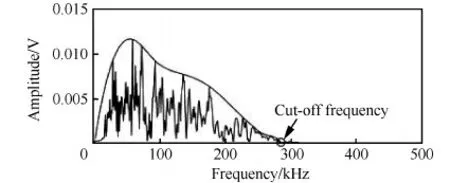
图12 信号截止频率 Fig.12 Cut-off frequency of signal

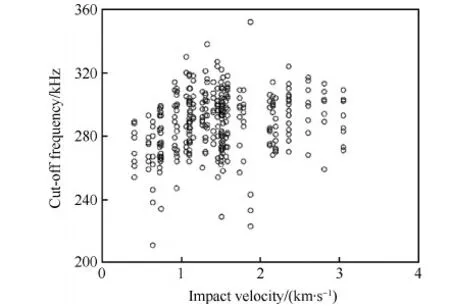
图13 信号截止频率与撞击速度的关系 Fig.13 Relationship between cut-off frequency of signal and impact velocity

2.4 小波特征参数

小波变换是时间频率的局部化分析，通过伸缩平移计算对信号进行逐步多尺度细化，可以将信号中各不同频率分量分离。根据2.3节的分析可知，蜂窝板面的超高速撞击声发射信号截止频率低于500 kHz，实验中数据采集设备的采样率为20 MHz，远高于信号的奈奎斯特采样频率，可将原始信号重采样至1 MHz，信号频率和波形特征与原信号吻合，因此可以降低小波分解次数，提高运算效率。采用小波变换对信号进行4层分解，第i层分解的系数进行重构可得到高频重构系数Di(n)和低频重构系数Ai(n)，则信号序列f(n)可以表示为各个重构系数之和，即

f(n)=D(n)+A(n)=D1(n)+(D2(n)+

(1)

重构信号将信号序列f(n)分解为不同尺度的5个分量。通过对比Ciofct、Haar、Symmlet、Daubechies、Demyer等小波基，发现采用4层Daubechies小波分解的结果最能反映信号各模态特征，分解结果如图14所示，分解后小波尺度如表2所示。

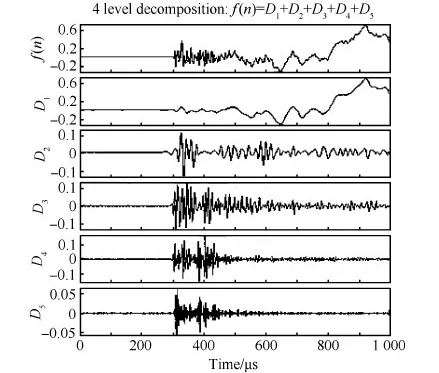
图14 超高速撞击声发射信号Daubechies 4小波4层分解 Fig.14 Daubechies 4 wavelet decomposition at level 4 of hypervelocity impact acoustic emission signal

表2 信号频带划分Table 2 Frequency band division of signal

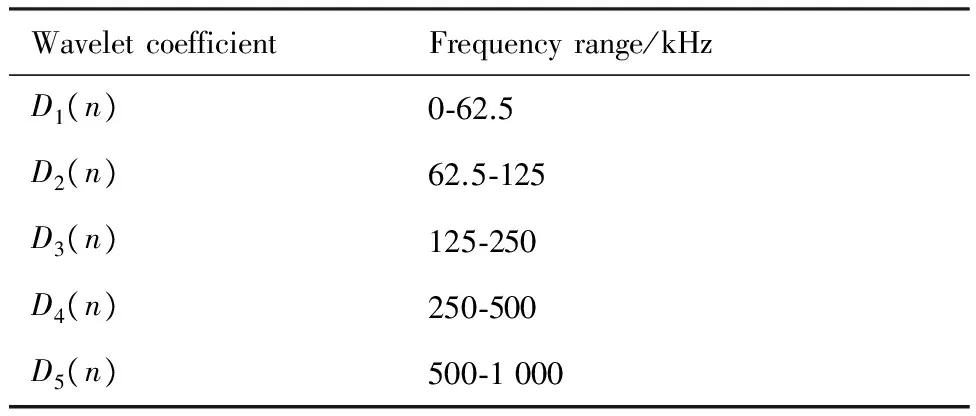
WaveletcoefficientFrequencyrange/kHzD1(n)0⁃62．5D2(n)62．5⁃125D3(n)125⁃250D4(n)250⁃500D5(n)500⁃1000

提出2种基于小波的特征参数：小波能量比和小波能量熵。

1) 自动加窗小波能量比

由于每次实验的安装有差异，各个传感器装置的预应力不同，且信号各个成分的能量随着传播距离的增加而不断变小，因此无法将信号能量的大小作为识别的参数，故提出一种小波能量比。

为了有效分析反射前的信号特征，采用2.2节如图10所示范围对前2个波包内的信号加窗，在自动时窗内能量满足E(f)=∑|f(n)|2<∞的前提下，各尺度的小波能量比可以写为

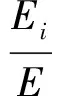
(2)

根据式(2)计算全部336组实验数据各小波各尺度的能量比，各能量比与撞击速度的关系如图15所示。

加窗后的小波能量比，D1(n)变化的范围最大，且分布较为分散，这主要是由于传播距离不同导致非超声部分信号的耦合程度不同，该值的大小受传播距离、撞击速度影响；D2(n)的分布比较特殊，其在1.5 km/s附近相对集中，越远离该速度越分散；D3(n)、D4(n)与D2(n)的分布规律相反，但3个分量的分布范围均主要在0～0.5；

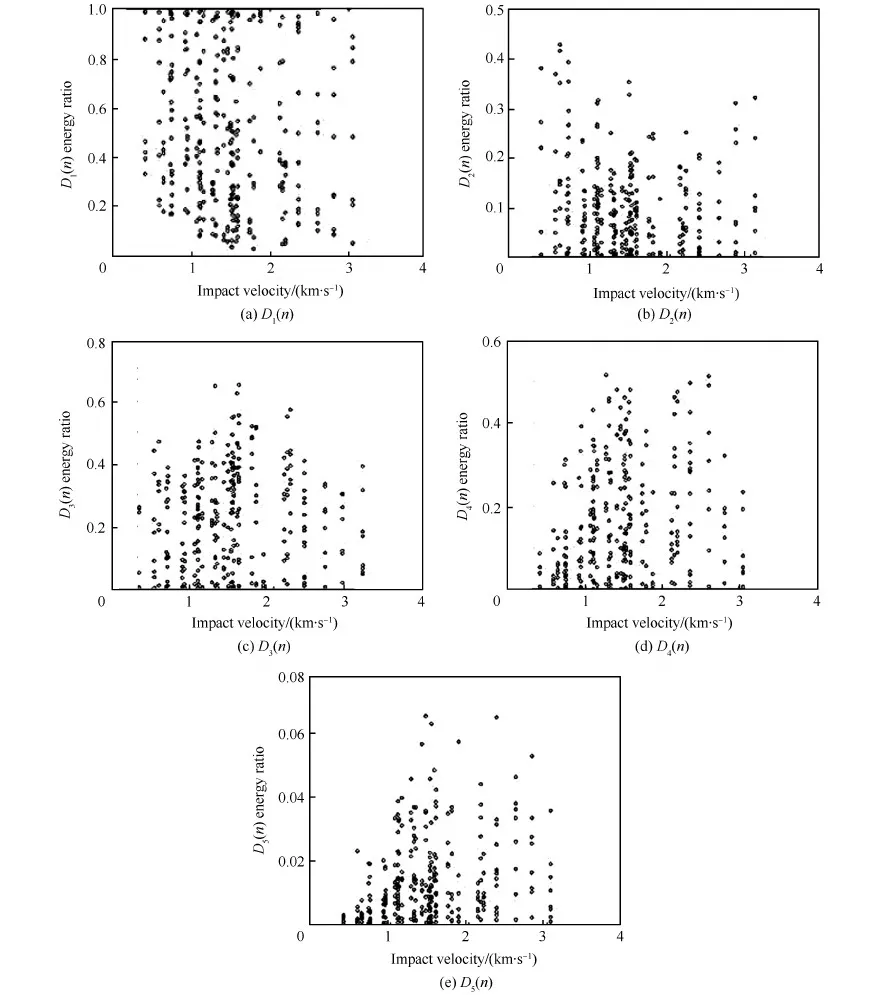
图15 各尺度小波能量比与撞击速度的关系 Fig.15 Relationship between wavelet energy ratio of every scalogram and impact velocity

D5(n)的变化范围最小，但在1 km/s以下明显有随着速度增大而范围增加的趋势，根据图3中撞击极限曲线可知，此时为成坑损伤，而1 km/s以上范围趋于稳定。

2) 小波能量熵

薄板中传播的超声波各个频率的分量衰减规律不同，且蜂窝板是各向异性材料，因此蜂窝板面上超高速撞击声发射信号是随着传播方向和距离变化的。假设信号经小波分解后，某尺度包含了Q个信号分量，频率分别为f1,f2,…，fQ，则各尺度下信号的能量比Pi可以写成方向di和角度θi的函数，即

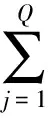
(3)

每一个频率分量的能量比都是随着传播方向和距离变化的。反之，针对已知载荷，若知道各尺度下信号的能量比，则传播距离及方向可以推测。

信息熵是信号不确定度的度量，用于表征信源输出的平均信息量大小。为了分析信号能量随频率范围分布的不确定度，用小波能量比代替信源各取值的概率，形成小波能量熵[18]，表征小波重构系数矩阵的稀疏程度。对超高速撞击声发射信号进行小波分解。小波分解后各尺度的能量比为Pi，则小波能量熵为

(4)

采用Daubechies 4小波对信号进行4层分解，得到5个尺度的重构信号，根据式(2)和式(4)计算得小波能量熵H，其与撞击速度的关系如图16 所示。

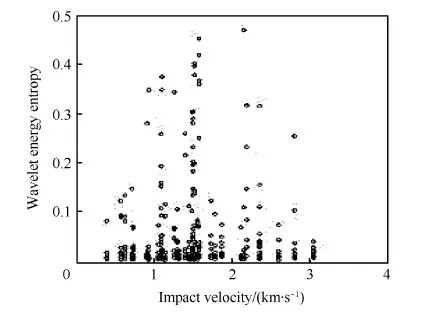
图16 小波能量熵与撞击速度的关系 Fig.16 Relationship between wavelet energy entropy and impact velocity

小波能量熵是随着撞击速度变化中心对称分布的，其中在1～2.2 km/s范围内变化范围最大。当撞击速度在1 km/s以下时形成成坑损伤，随着速度的不断增加小波能量熵变化的范围逐渐变大，说明随着损伤不断加剧，信号的复杂程度也不断增加；在1～2.2 km/s范围内，撞击的动能主要作用于蒙皮面板上，信源强度和振动的复杂程度都保持在一个较稳定的范围；当撞击速度大于2.2 km/s 时，一部分能量以碎片云的形式与蜂窝板脱离，导致信号的复杂程度降低了。

3 参数检验

根据第2节对各特征参数的分析，无法直接建立各特征参数与损伤之间的联系，因此需要使用模式识别方法建立特征多参数组合与损伤的关系。为评价各特征参数在损伤模式识别中的作用，优选损伤模式识别参数，使被选择的参数既能体现同一类别的相似性，又能体现不同类别的差异性，采用Kruskal-Wallis(KW)检验对参数进行评价。

Kruskal-Wallis检验对于区分总体分布未知的多个量是否存在显著差异有一定优越性，其原理是选取各特征中每个类别的编号均值，通过比较每个类别平均值之间的距离评价该样本对分类的贡献，即评价某个特征参数分类能力的相对大小。

分别检验本文提出的9个特征参数，选择样本为第2节中对全部336组实验信号分析所得各个参数的计算值，采用SPSS软件计算每个参数的KW检验统计量和渐进显著性指标，结果如表3 所示。其中KW值为Kruskal-Wallis检验

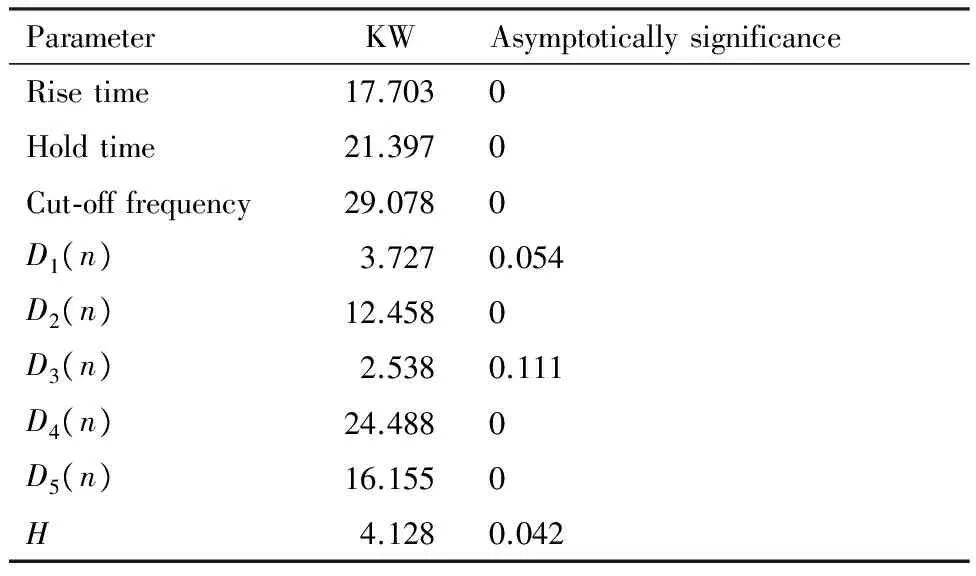
表3 Kruskal-Wallis(KW)检验结果Table 3 Results of Kruskal-Wallis (KW) test

的结果，该值越大表示分类能力越好；渐进显著性指标表征样本分布是否满足正态分布，参数的显著性水平越低，置信度越高，分类能力越好。

上升时间、持续时间、截止频率、D2(n)、D4(n)和D5(n)这6个参数的渐进显著性指标为0，符合正态分布，且KW检验值较高；H的显著性水平为0.042，满足正态分布；D1(n)的显著性水平为0.054，近似满足正态分布；D3(n)显著性水平为0.111，不满足正态分布。

综上可知，上升时间、持续时间、截止频率、小波能量比(D2(n)、D4(n)、D5(n))和小波信息熵共7个特征参数差异性较小，可作为损伤模式识别中的参数；小波能量比(D1(n)、D3(n))能否作为损伤模式识别参数，需要在算法中验证得知。

4 损伤模式识别

4.1 算法设计

采用贝叶斯正则化的神经网络模型处理该多参数的损伤模式识别问题。

BP神经网络指的是基于BP算法的多层向前神经网络，通过误差控制信息的传递，当输出结果误差大于期望值时，误差以一种形式通过隐含层向输入层返回，修正网络权值。

正则化方法可以很好地提高网络的泛化能力，贝叶斯正则化算法是在一种变形的牛顿法(Levenberg-Marquardt，LM)基础上进行修正的网络算法，通过修正神经网络的性能函数来提高优化能力[19-21]。该算法在LM算法的性能函数误差反馈的基础上，加入权值的反馈，其网络的训练函数可以写成

F=αEω+βED

(5)

式中：Eω为全部网络权值平方和；ED为每层网络输出值与真实值之间的误差值；α和β分别为性能函数的正则化系数，表达式为式(6)。系数的值代表网络训练的侧重，当α<β时，随着训练次数的增加，训练样本的误差逐渐变小；当α>β时，随着训练次数的增加，权值逐渐变小，平滑网络输出。

(6)

式中：γ为有效参数的数量，表征能够降低训练误差的神经网络的连接权值数量；n为全部的训练样本数量。

γ=n-2αtr(H-1)

(7)

其中：H为性能函数的海森矩阵，且

(8)

优选网络结构，经对比测试发现，当选择贝叶斯正则化神经网络结构，网络包含4个隐含层，每层10个节点，学习函数为S型对数函数，传递函数为梯度下降法时，网络识别能力最优，运算效率最高。

对损伤模式识别特征参数进行优选，根据各特征参数的类型和表4中的检验结果，设计了9个参数组合方式，用于对比和提炼最优参数组合，如表4所示。

为评估神经网络的识别能力及由识别误差带来的风险，深入分析对成坑、穿孔2种损伤模式的区分能力，使用4个识别指标：穿孔识别率、成坑识别率、错分率和风险，并用误差平方和表示计算结果的稳定性，网络计算值与期望值间允许的最大误差K取0.2。其中成坑识别率Ppit代表了全部成坑样本中识别正确的百分比，即

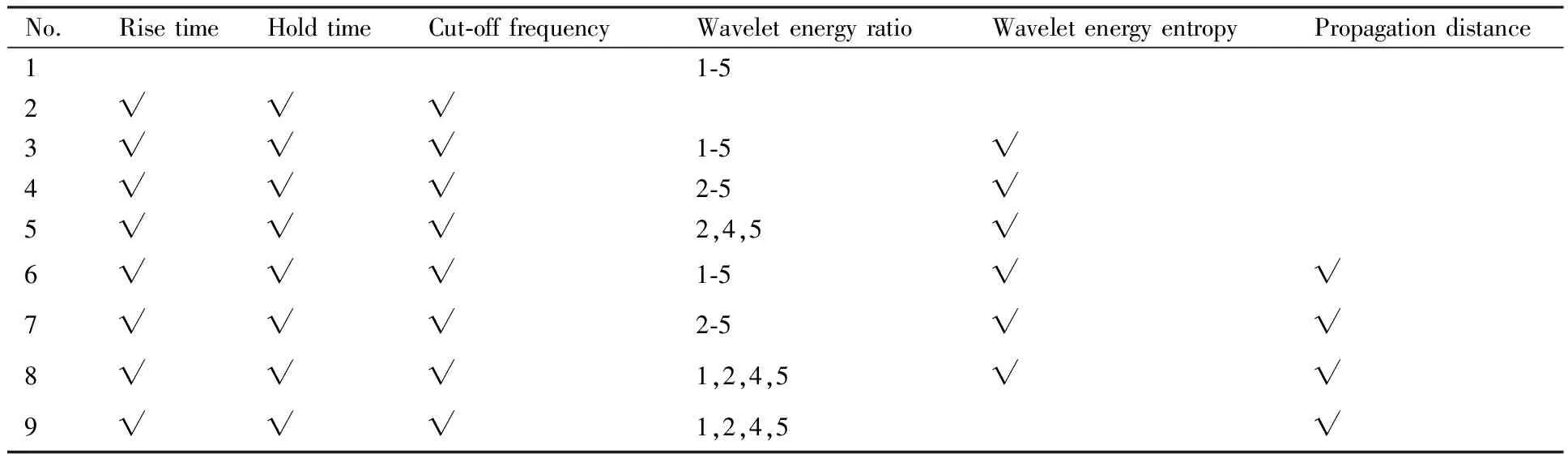
表4 输入参数列表Table 4 List of input parameters

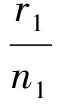
(9)

穿孔识别率Phole代表了全部穿孔样本中识别正确的百分比，即

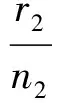
(10)

式中：n1为成坑样本数；n2为穿孔样本数；r1为识别成坑正确的样本数；r2为识别穿孔正确的样本数。

错分率Erate代表全部识别样本中未能正确识别的百分比，是损伤模式识别中的一个重要指标，主要考虑错误分类后的不同结果，其为

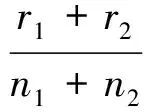
(11)

风险Risk是基于最小风险准则的一个指标，指靶板发生穿孔被误识别为成坑损伤的百分比，其为

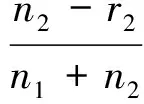
(12)

对336组实验数据进行自识别，表5为损伤模式识别方法对表4中参数组合的20次训练后的最优识别结果。

分析表5可得结论如下：

1) 对比参数组合1、组合2和组合6的识别结果可知，当单独使用小波能量比或时频参数识别时，误差平方和较大，算法稳定性低，但对穿孔

表5训练样本损伤模式识别结果的识别能力较高，这主要是因为穿孔样本数远多于成坑样本。

Table5Damagepatternrecognitionresultsoftrainingsamples

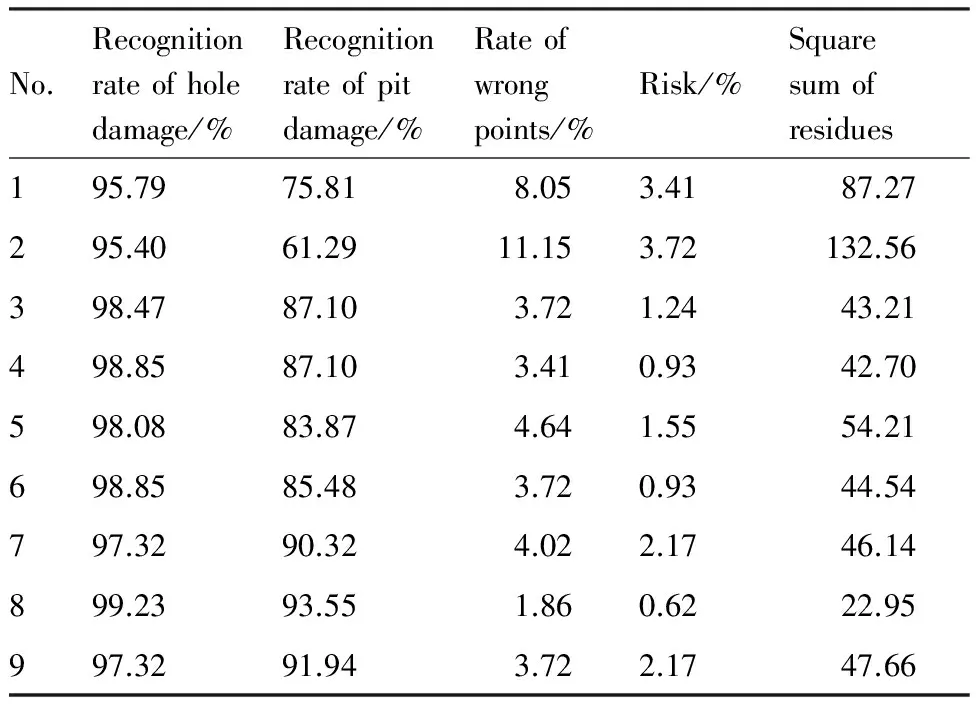
No．Recognitionrateofholedamage/%Recognitionrateofpitdamage/%Rateofwrongpoints/%Risk/%Squaresumofresidues195．7975．818．053．4187．27295．4061．2911．153．72132．56398．4787．103．721．2443．21498．8587．103．410．9342．70598．0883．874．641．5554．21698．8585．483．720．9344．54797．3290．324．022．1746．14899．2393．551．860．6222．95997．3291．943．722．1747．66

2) 对比参数组合3和组合4的识别结果可知，在不考虑传播距离的前提下，D1(n)对损伤模式识别影响较小，使穿孔识别能力有小幅下降，但对比组合4和组合7可知，加入传播距离参数后，成坑识别能力提升较大。

3) 对比参数组合6和组合8的识别结果可知，特征参数D3(n)在与传播距离参数同时存在时，使组合的成坑和穿孔识别能力均有一定程度的降低，因此将其认作为干扰参数。

4) 加入传播距离参数后，各组的成坑识别能力均有一定提升，识别结果多数高于90%，因此认为传播距离是有效的参数。

5) 对比参数组合8和组合9的识别结果可知，小波能量熵对信号的识别能力有较小的提升，去掉后成坑、穿孔的识别能力均下降约2%。

由于特征参数均是随着传播距离变化的量，但传播距离自身与损伤无关，针对是否使用传播距离选取2个识别结果较好，且算法稳定性较高的参数组合为组合4和组合8。

4.2 算法验证

为评价损伤模式识别算法的能力，需使用非同源样本进行验证。从表1中随机抽取4次实验作为验证数据，包含3次穿孔损伤和1次成坑损伤，如表6所示，共32组实验数据，神经网络训练选取余下的304组数据。

采用本文的损伤模式识别方法，验证结果如表7所示，表7中No.1和No.2分别为表4中No.4和No.8特征参数组合的识别结果。

结果表明，本文建立的贝叶斯正则化BP神经网络可以用于识别非同源的蜂窝板超高速受超高速撞击事件。对于非同源的实验数据，选择由传播距离、上升时间、持续时间、截止频率、自动加窗小波能量比(D1(n)、D2(n)、D4(n)、D5(n))、小波信息熵构成的特征参数组合识别的结果比较好。

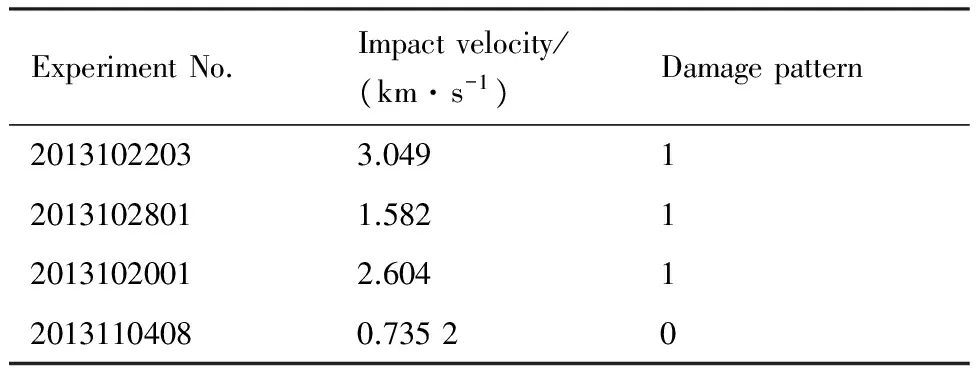
表6 验证实验工况Table 6 Confirmatory experiment condition

表7最优参数损伤模式识别结果

Table7Damagepatternrecognitionresultsoftheoptimalparametercombination

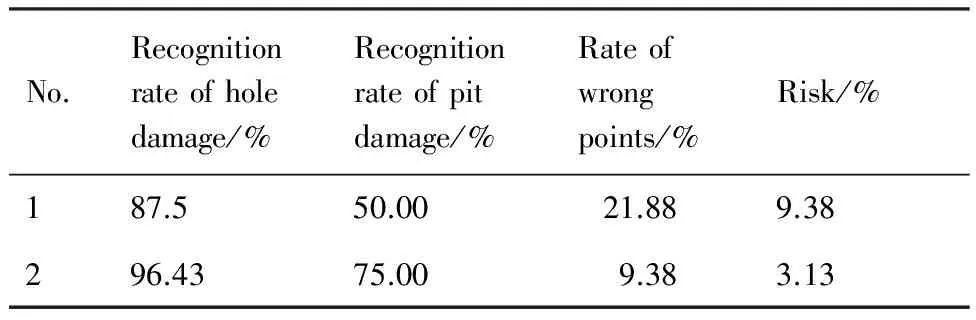
No．Recognitionrateofholedamage/%Recognitionrateofpitdamage/%Rateofwrongpoints/%Risk/%187．550．0021．889．38296．4375．009．383．13

由于在实验环境中获得1 km/s以下撞击速度较困难，使针对成坑损伤的实验量不充分，导致了成坑识别准确率始终低于穿孔，在此基础上如进一步补充该范围实验，可以有效提高对成坑损伤的识别能力。

5 结 论

在实验的基础上，提出了一种基于声发射技术的蜂窝板受超高速撞击损伤模式识别方法，并通过非同源样本验证识别方法的有效性，得主要结论如下：

1) 传播距离是蜂窝板面超高速撞击损伤模式识别的重要参数，在算法中必须予以考虑。

2) 加窗后的小波能量比是损伤模式识别的重要参数，与传播距离组合可以有效提高识别能力，但其中的D3(n)对识别有一定干扰。

3) 小波能量熵对损伤模式识别有一定的提升作用，可以作为损伤模式识别的参数。

4) 0～62.5 kHz频域的加窗小波能量比对穿孔识别能力有一定提升，但会降低对成坑的识别能力。

5) 蜂窝板受超高速撞击损伤模式识别的最优参数组合为传播距离、上升时间、持续时间、截止频率和自动加窗小波能量比(D1(n)、D2(n)、D4(n)、D5(n))及小波能量熵，基于该组合的贝叶斯正则化神经网络可以有效识别成坑和穿孔2种损伤模式。

[1] Upper stage explosion places LEO satellites at risk[N]. Orbital Debris Quarterly News, 2013-01-17.

[2] LIOU J C, GIOVANE F, CORSARO R, et al. LAD-C—A large area debris collector on the ISS[C]//36th COSPAR Scientific Assembly. Paris: Committee on Space Research (COSPAR), 2006.

[3] PROSSER W H, MADARAS E I. Distributed impact detector system (DIDS) health monitoring system evaluation: NASA/TM-2010-216694[R]. Hampton, VA: Langley Research Center, 2010.

[4] SPENCER G, SCHAFER F, TANAKA M, et al. Design and initial calibration of micrometeoroid space debris detector (MDD)[C]//Proceedings of the 4th European Conference on Space Debris. Pairs: European Space Agency, 2005, 587: 2275.

[5] SCHAFER F, JANOVSKY R. Impact sensor network for detection of hypervelocity impacts on spacecraft[J]. Acta Astronautica, 2007, 61(10): 901-911.

[6] SCHWANETHAL J P, MCBRIDE N, GREEN S F, et al. Analysis of impact data from the DEBIE (debris in-orbit evaluator) sensor in polar low earth orbit[C]//Proceedings of the 4th European Conference on Space Debris. Pairs: European Space Agency, 2005, 587: 177.

[7] 唐颀, 庞宝君, 韩增尧, 等. 单层板超高速撞击声发射波的频谱特征分析[J]. 宇航学报, 2007, 28(4): 1059-1064.

TANG Q, PANG B J, HAN Z Y , et al. Analysis of frequency spectrum character of acoustic emission wave from hypervelocity impact on single-sheet plate[J]. Journal of Astronautics, 2007, 28(4): 1059-1064 (in Chinese).

[8] 王晓宇, 张超, 孙维, 等. 航天器密封舱加筋壁板碎片撞击监测技术研究[J]. 实验流体力学, 2014, 28(4): 70-77.

WANG X Y, ZHANG C, SUN W, et al. Research on structural health monitoring method for locating space debris impact on spacecraft seal structure[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(4): 70-77 (in Chinese).

[9] 刘武刚, 庞宝君, 韩增尧, 等. 基于小波分析技术的高速撞击声发射源定位[J]. 高技术通讯, 2009, 19(2): 181-187.

LIU W G, PANG B J, HAN Z Y, et al. Acoustic emission detection and location for hypervelocity impacts based on wavelet transform[J]. Chinese High Technology Letters, 2009, 19(2): 181-187 (in Chinese).

[10] LIU Z D, PANG B J. A method based on acoustic emission for locating debris cloud impact[C]//Proceedings of the SPIE 7522, 4th International Conference on Experimental Mechanics. Bellingham, WA: SPIE, 2010.

[11] 庞宝君, 刘治东, 唐颀. 基于HHT变换的声发射源平面定位方法[J]. 无损检测, 2010(1): 1-5.

PANG B J, LIU Z D, TANG Q. A method based on HHT for acoustic emission source location[J]. Nondestructive Testing, 2010(1): 1-5 (in Chinese).

[12] 张凯, 庞宝君, 林敏. 碎片云撞击声发射信号能量特征小波包分析[J]. 振动与冲击, 2012, 31(12): 125-128.

ZHANG K, PANG B J, LIN M. Wavelet packet analysis for acoustic emission signals caused by debris cloud impact[J]. Journal of Vibration and Shock, 2012, 31(12): 125-128 (in Chinese).

[13] 熊秋鹏. 基于神经网络技术的空间碎片损伤模式识别研究[D]. 哈尔滨: 哈尔滨工业大学, 2012: 31-35.

XIONG Q P. Research on space debris damage pattern recognition based on neutral network technology[D]. Harbin: Harbin Institute of Technology, 2012: 31-35 (in Chinese).

[14] EMMA A T, JONATHAN P G, CLEGG R A, et al. Hypervelocity impact on spacecraft honeycomb: Hydrocode simulation and damage laws[J]. International Journal of Impact Engineering, 2003, 29(1-10): 691-702.

[15] ALAVI N A, RAZAVI S B, MAJZOOBI H H. Ballistic limit determination of aluminum honeycombs—Experimental study[J]. Materials Science and Engineering A, 2008, 488(1): 273-280.

[16] LIU Y, PANG B J, JIA B, et al. Modal acoustic emission based location method in honeycomb core sandwich structure[C]//Proceedings of the 6th European Conference on Space Debris. Pairs: European Space Agency, 2013, 723: 183.

[17] CHAKRABORTY N, RATHOD V T, MAHAPATRA D R, et al. Guided wave based detection of damage in honeycomb core sandwich structures[J]. NDT&E International, 2012, 49(7): 27-33.

[18] ROSSO O A, BLANCO S, YORDANOVA J, et al. Wavelet entropy: A new tool for analysis of short duration brain electrical signals[J]. Journal of Neurosci Methods, 2001, 105(1): 65-75.

[19] MACKAY D J C. Bayesian interpolation[J]. Neural Computation, 1992; 4(3): 415-447.

[20] ORRE R, LANSNER A, BATE A, et al. Bayesian neural networks with confidence estimations applied to data mining[J]. Computational Statistics & Data Analysis, 2000, 34(4): 473-493.

[21] WONG B M L， LEE S Y， LEUNG K S. Data mining of Bayesian networks using cooperative coevolution[J]. Decision Support Systems, 2004, 38(3): 451-472.

(责任编辑： 徐晓)

URL：www.cnki.net/kcms/detail/11.1929.V.20170303.1902.002.html

Adamagepatternrecognitionmethodforhypervelocityimpactonaluminumhoneycombcoresandwichbasedonacousticemission

LIUYuan,PANGBaojun,CHIRunqiang*,CAIYuan

SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150080，China

Adamagepatternrecognitionmethodbasedonneuralnetworkisproposedtorecognizethedamagestateofaluminumhoneycombcoresandwichunderhypervelocityimpact(HVI)throughacousticemission.Avarietyofexperimentalsignalsareobtained,10characteristicparametersrelatedtodamagearepresentedbytestofnonparametricanalysistherelationshipwithdamagepattern,combiningwithprecisesourcelocalization,time-frequencyanalysis,wavelettransformationandmodalacousticemissiontechnology.TheBPneuralnetmodebasedonBayesianregularizationisestablishedbyanalyzingtherelationshipwithdamagepatternusingnonparametricanalysis.Afterestablishingtheoptimalnetworkmodel,twooptimalcombinationsareselectedbyanalyzingtherecognitionabilityofdifferentparametercombinations,thedamagepatternrecognitionabilityisverifiedwithnon-samesourcesample.Theresultshowsthatpropagationdistanceisasignificantparameterbutirrelevanttodamagepattern.Automaticwindowwaveletenergyratiowithin125-250kHzfrequencyrangedecreasetheabilityofdamagepatternrecognition.UsingaBayesianregularizationneuralnetworkwithcombinationof9parameters,includingpropagationdistance,risetime,holdtime,cut-offfrequency,4kindsofautomaticwindowwaveletenergyratioandwaveletenergyentropy,presents9.38%wrongpointratetoagroupofrandomnon-samesourcesample.

spacedebris;hypervelocityimpact(HVI);acousticemission;damagepatternrecognition;neuralnetwork

2016-05-05；Revised2016-10-19；Accepted2017-02-13；Publishedonline2017-03-031902

s：NationalSpecialProjectforSpaceDebrisduringtheTwelfthFive-yearPlanPeriod(K0203210);theFundamentalResearchFundsforCentralUniversities(HIT.NSRIF.2015029)

.E-mailchirq@hit.edu.cn

2016-05-05；退修日期2016-10-19；录用日期2017-02-13； < class="emphasis_bold">网络出版时间

时间：2017-03-031902

www.cnki.net/kcms/detail/11.1929.V.20170303.1902.002.html

国家“十二五”空间碎片专项 (K0203210)； 中央高校基本科研业务费专项资金 (HIT.NSRIF.2015029)

.E-mailchirq@hit.edu.cn

刘源， 庞宝君， 迟润强， 等． 基于声发射的铝蜂窝板超高速撞击损伤模式识别方法J． 航空学报,2017,38(5):220401.LIUY,PANGBJ,CHIRQ,etal.AdamagepatternrecognitionmethodforhypervelocityimpactonaluminumhoneycombcoresandwichbasedonacousticemissionJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):220401.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.220401

V19； X949

A

1000-6893(2017)05-220401-13