基于前缘缝翼微型后缘装置的多段翼型被动流动控制

张振辉， 李栋， 杨茵

西北工业大学 翼型叶栅空气动力学国家重点实验室， 西安 710072

基于前缘缝翼微型后缘装置的多段翼型被动流动控制

张振辉， 李栋*， 杨茵

西北工业大学 翼型叶栅空气动力学国家重点实验室， 西安 710072

以麦道航空公司的三段增升构型为研究模型，采用剪切应力输运(SST)k-ω湍流模型在C-H型多块结构网格上求解二维非定常雷诺平均Navier-Stokes方程，研究了前缘缝翼微型后缘装置(MTED)在多段翼型被动流动控制中的应用。由于MTED改变了实际的缝翼缝道参数，因此首先研究了作为主要改变量的缝道宽度对该三段翼型气动性能的影响，当缝道宽度从参考构型的2.95%c增加至3.98%c时，最大总升力系数约减小4.61%。当在不同缝道宽度基本构型上增加相同MTED时，计算结果表明它对各个翼段的影响定性一致，即前缘缝翼升力增加、主翼升力减小以及后缘襟翼升力基本不变化。这些升力变化的综合作用是：MTED构型线性段总升力系数的变化不大，失速段的变化取决于缝道宽度，当缝道宽度为3.98%c时，高度为0.50%c的MTED构型的最大总升力系数约增加6.98%。

多段翼型； 被动流动控制； 前缘缝翼； 微型后缘装置(MTED)； 缝道宽度

现代大型飞机离不开高效的增升装置，它能够改善飞机的起降和爬升性能、提高起飞重量、缩短滑跑距离、减小气动噪声以及增强机场适应性等[1]。因此，飞机制造商都在不遗余力地推进增升装置技术的发展，它的发展趋势是气动外形的高效化和结构设计的简单化，如B727采用了内侧克鲁格襟翼和外侧前缘缝翼的前缘增升装置以及三缝襟翼后缘增升装置，而B767对应的则是前缘缝翼以及内侧双缝襟翼和外侧单缝襟翼[2]。传统增升装置的设计经历了不断发展后，在气动性能上的改进空间已变得非常有限，适用的流动控制技术为其提供了一种有效途径。

基于能量消耗和控制环路的方式，增升装置的流动控制技术可分为被动和主动控制技术，被动控制装置包括主翼下偏扰流板[3]、主翼增升薄片[4]、襟翼微型后缘装置[5]以及主翼和襟翼涡流发生器[6]等，涉及的主动控制手段包括合成射流[7]、等离子体[8]以及动力增升[9]等。这两种控制技术各有自身特点和机理，其中被动控制具有无需外部能源、技术相对简单、制造成本较低以及技术成熟度高等优点，已在某些型号的飞机上得到了应用，如F-18中的下偏扰流板。在上述增升装置的被动控制装置中，实际上主翼增升薄片也属微型后缘装置(MTED)的范畴，MTED在几何尺度上与边界层高度为同一量级，可以布置在不同翼段或组合使用，根据实际飞行状态打开和收起都比较方便。

对于MTED在多段翼构型[4-5，10-12]上的应用研究，主要集中在主翼和襟翼上，Carrannanto等[11]分析了两段翼型和三段翼型主翼MTED对气动性能的影响，褚胡冰等[5]分析了三段翼型襟翼MTED几何参数的影响。对于现代民用飞机，传统的增升装置大多采用前缘缝翼和后缘襟翼的形式，前缘缝翼在延迟流动分离和增大失速迎角方面具有重要作用。因此，本文以麦道航空公司的三段增升构型为研究模型，结合缝翼缝道参数的变化，研究了缝翼MTED在多段翼型被动流动控制中的应用，旨在分析并总结它的控制机理和影响规律。

1 研究模型

麦道航空公司的三段增升构型被广泛采用于多段翼型的数值研究[13]中，曾作为1993年在NASA Langley研究中心举办的高升力研讨会的算例[14]。它的风洞试验[15-16]主要在NASA Langley研究中心的低湍流度增压风洞(LTPT)中完成，涵盖了不同雷诺数以及不同缝翼和襟翼缝道参数构型。各个翼段打开时它的缝道参数采用“正交法”定义，如图1所示，各个翼段收起时的巡航状态翼型参考弦长为c。前缘缝翼缝道参数包括缝翼偏角δs、缝翼重叠量Os和缝翼缝道宽度Gs；后缘襟翼缝道参数与此类似，包括襟翼偏角δf、襟翼重叠量Of和襟翼缝道宽度Gf。前缘缝翼MTED布置在缝翼后缘的下表面，考虑到局部网格的生成及其质量将它大致设置为沿当地翼面的法线方向，它的宽度为0.04%c，高度定义为h。

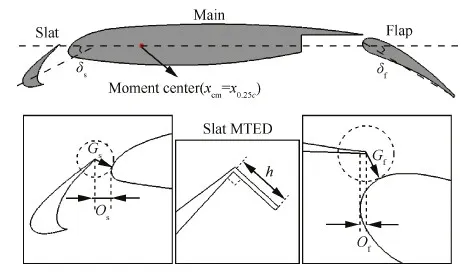
图1 研究模型及参数定义 Fig.1 Research model and parameters definition

2 数值方法及验证

2.1 数值方法

本文数值模拟基于成熟的ANSYS Fluent软件[17-18]，采用有限体积法求解二维非定常雷诺平均Navier-Stokes (RANS) 方程，对流项采用二阶迎风格式，扩散项采用二阶中心差分格式，时间推进采用隐式双时间推进方法。为了使RANS方程封闭，采用剪切应力输运(SST)k-ω两方程湍流模型(假定全湍计算)，Rumsey和Ying[13]在对多段翼型数值模拟进行的总结中发现该湍流模型对多段翼型的数值计算比较准确。边界条件的设定为：物面采用无滑移边界条件，远场采用压力远场边界条件。计算马赫数和雷诺数分别为Ma=0.2和Re=9.0×106，其中雷诺数参考长度为巡航构型的翼型弦长c。在计算过程中，无量纲化所使用的参考面积和参考长度都为巡航状态的对应值；力矩中心xcm定义的位置如图1所示，它位于巡航构型的0.25c处。

2.2 计算网格

计算域远场边界由半圆和矩形组成，多段翼型上游和上下边界取为15c，下游取为20c；数值计算采用的C-H型多块结构网格的网格拓扑结构及物面附近网格如图2所示。每个翼段都以C型网格为主导，其中缝翼、主翼和襟翼C型网格的数量分别为2、1和1，此外在网格拓扑结构上布置了可以表征缝道宽度的“过渡层”。当缝道宽度变化时，保持各个翼段壁面附近的局部网格不变，仅通过调节“过渡层”区域的局部网格即可得到全局网格。

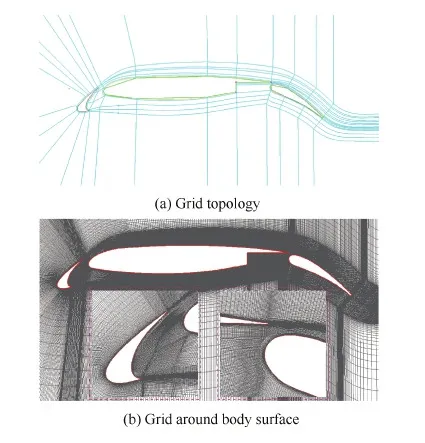
图2 C-H型多块结构网格 Fig.2 Multi-block structured grid of C-H type

为了研究网格敏感性，选取30P30N基本构型，在不改变计算域分块的前提下，通过调节每个块内部的网格节点分布得到几套不同疏密的网格，然后进行对比计算。首先建立一套粗网格(Coarse Grid)，在此粗网格上分别沿着翼型法向和流向加密得到中网格A(Medium Grid A)和中网格B(Medium Grid B)，同时沿这2个方向加密得到细网格(Refined Grid)。这几套网格的分块过渡遵循相同的原则，物面第一层网格的高度都约为1.0×10-5c，网格数量情况如表1所示。计算结果的比较如图3所示，从图中可以看出：它们对升阻力系数CL和CD、力矩系数Cm和表面压力系数Cp分布具有相同的解析度，后文中的数值计算都采用网格数量较大的细网格。类似地，对于MTED附近的局部网格敏感性也进行了研究，并依据计算结果选择合适的网格。

表1 几套不同疏密的网格(30P30N)Table 1 Several sets of grid with different size (30P30N)

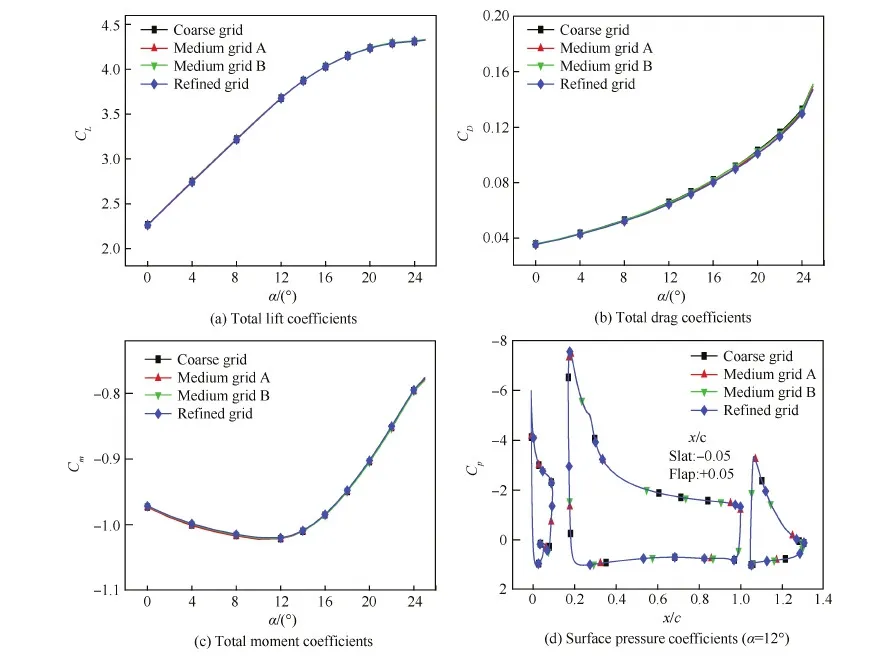
图3 几套不同疏密网格的计算结果比较(30P30N) Fig.3 Comparison of calculation results from several sets of grid with different size (30P30N)

2.3 数值验证

为了验证计算方法，选用研究模型的典型着陆构型30P30N作为算例，该构型的缝道参数为：前缘缝翼δs=30°,Gs=2.95%c,Os=-2.50%c;后缘襟翼δf=-30°,Gf=1.27%c,Of=0.25%c。在实验中虽然采用了侧壁吸气的方法来尽可能地保证二维流动特性，但襟翼上表面的展向压力分布表明当α>16° 时流动的三维效应较强，这会对计算与实验的比较产生一定的影响。

计算与实验结果的比较如图4所示，图4(a)为升力系数[15-16]，当α<16° 时二者吻合良好；实验失速迎角和最大总升力系数分别约为21°～22° 和4.37，计算的失速过程相对缓慢，对应的这些计算值约为24°～25° 和4.32，计算的失速迎角偏大，最大总升力系数吻合。主翼是该构型最主要的升力部件，实验中当α≈21° 时主翼失速，随着迎角的继续增加主翼升力系数较快地减小；计算的主翼失速迎角与实验值相同，但主翼失速过程相对缓慢。前缘缝翼和后缘襟翼计算升力系数的变化与相应的实验结果一致，各个翼段的综合作用使总升力系数的计算值在失速迎角附近与实验值有一定的偏差。

图4(b)为阻力系数[15]，计算值与实验值之间的偏差较大，与Wang等[3]的计算值吻合。王运涛等[19]指出：采用全湍流模拟方式对多段翼型边界层速度型和阻力系数的模拟精度较差，模拟实验的转捩位置可以使计算结果更接近实验值，但还是存在一定的差距。

图4(c)为俯仰力矩系数[14]，负值表示低头力矩，实验结果显示在失速前随着迎角的增加低头力矩减小，计算值与实验值基本吻合。实验结果指出力矩减小的原因是：随着迎角的增加，缝翼升力增加，襟翼升力减小；主翼前缘的吸力峰值显著增加，主翼后部的升力变化相对较小，这些计算结果都与相应的实验结果吻合。

图4(d)为α=16°时的表面压力分布[15]，各个翼段的计算结果均与相应的实验结果吻合良好。实验结果表明在失速迎角附近这个构型在各个翼段的上表面均没有出现明显的分离区；计算结果也是如此，当α>20°时主翼尾迹分离，随着迎角的进一步增加分离区逐渐增大。

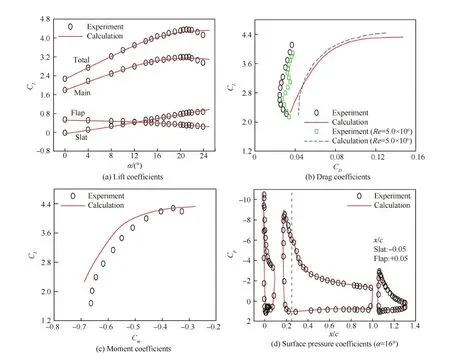
图4 30P30N构型计算与实验结果[14-15]的比较 Fig.4 Comparison between calculation and experiment results[14-15] for 30P30N configuration

3 计算结果及分析

根据图1中的定义，多段翼型前缘缝翼MTED改变了实际的缝翼重叠量Os和缝道宽度Gs，其中主要改变了Gs。因此，研究基于它的多段翼型被动流动控制需要考虑缝翼缝道参数这个因素，下面首先研究Gs对气动性能的影响，然后分析MTED的控制机理并总结其影响规律。

3.1 前缘缝翼缝道宽度的影响

为了研究前缘缝翼缝道宽度Gs的影响，保持前缘缝翼偏角δs和重叠量Os以及后缘襟翼缝道参数不变，分别将Gs/c设定为2.95%、3.17%、3.41%、3.68%和3.98%。实际上，相对30P30N参考构型后4个构型的缝翼分别沿远离主翼轴线的方向平移0.5%c、1.0%c、1.5%c和2.0%c。

由于中间3个Gs基本构型的计算结果基本上介于最小和最大Gs基本构型之间，因此仅给出了最小和最大Gs情形的对比结果。图5为力和力矩系数，随着Gs的增加，缝翼升力系数在整个计算迎角范围内都减小，且减小量随着迎角的增加而逐步增加。主翼升力系数在α<14° 时的线性段增加，但随着迎角的继续增加升力线斜率较快地减小而使升力系数小于参考构型。襟翼升力系数在α<10° 时几乎没有变化，但随着迎角的进一步增加它逐步小于参考构型。图5(a)～图5(c)的坐标尺度相同，对比三图可以发现：在相同迎角下，缝翼升力的减小量在3个翼段中始终最大，其中襟翼升力的变化不起主导作用。因此，3个翼段的总升力系数在所有计算迎角下都小于参考构型，当α≤8° 时它的减小量很小，但随着迎角的继续增加总升力系数逐渐减小，失速性能降低，表现为：失速迎角呈减小的趋势，相比参考构型Gs=3.98%c构型的最大总升力系数约减小4.61%。此外，3个翼段的总阻力系数在不同迎角下都增加，除失速迎角附近外每个迎角下的阻力增量几乎相同；俯仰力矩的变化是各个翼段升力变化和它们到力矩中心距离综合作用的结果，在计算迎角范围内总低头力矩都不同程度地增加。

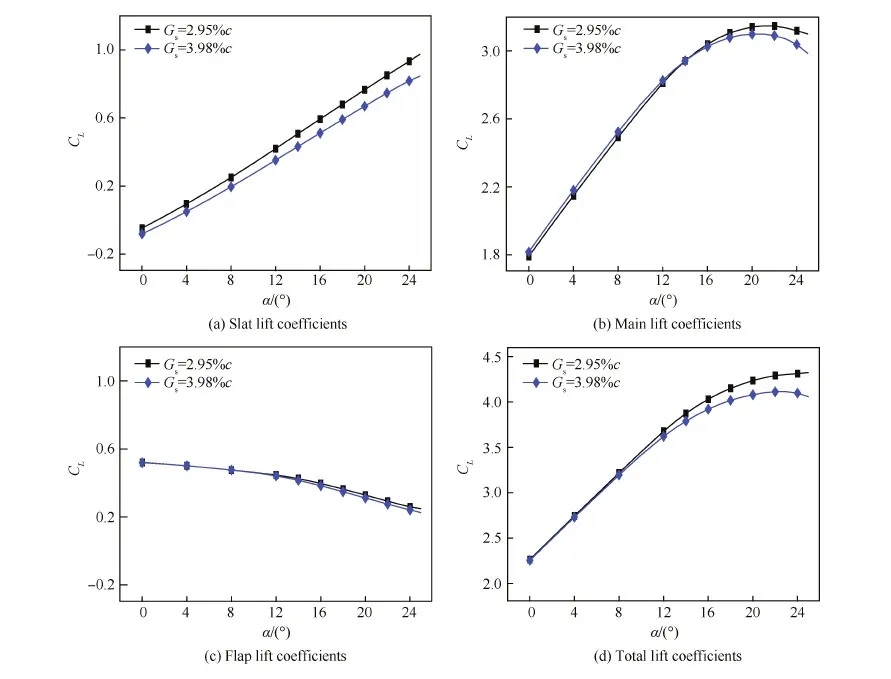
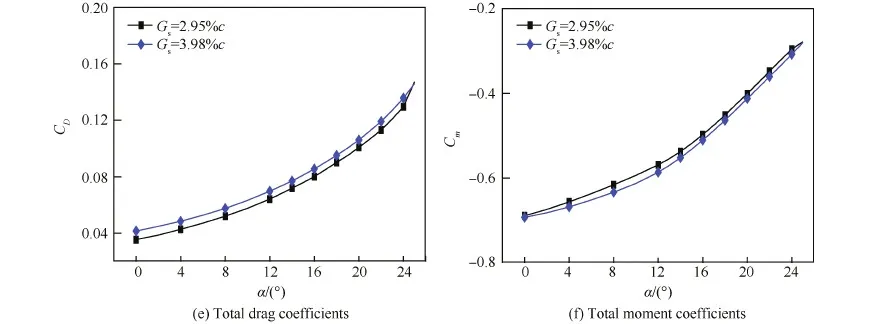
图5 不同缝道宽度基本构型的力和力矩系数 Fig.5 Coefficients of force and moment for baseline configurations with different slat gap

在不同迎角下，随Gs的增加上述计算结果的变化从某种程度上来说是定性一致的，图6给出了计算迎角范围的中间值α=12° 时上述两种基本构型的相应结果。图6(a)为升阻系数和升阻比K随Gs的变化曲线，总升力系数和升阻比的变化趋势一致，它们都随Gs的增加而非线性地减小，而总阻力系数与此相反，因此Gs=2.95%c是这些Gs中的最优值。图6(b)为不同Gs构型的流线和马赫数云图，两图中的流线均来自于上游的相同位置，随着Gs的增加更多流体流经缝翼缝道，其中部分流体需要偏转更大的角度才能通过缝道，因此阻力增加。两图中马赫数云图的等值线划分相同，当Gs增加时，缝翼驻点前移，缝翼迎风面驻点之后和背风面凹陷处的绕流以及缝道内流动的马赫数增加，这使得相应位置的压力分布(表面压力分布见图6(c))减小；缝翼上表面前缘附近绕流的流速减小，这对应缝翼吸力峰值的减小；缝翼上表面后缘附近的吸力增加，在这些因素的综合作用下缝翼升力减小。缝翼升力减小使缝翼尾迹气流的下洗作用减弱，主翼上表面前缘附近绕流的流速增加，这对应主翼吸力峰值的增加；主翼上表面除前缘附近之外的其余部分的吸力稍有减小，主翼下表面的压力分布基本没有变化；主翼前缘附近的升力增量明显大于其余部分的升力减量，因此主翼升力增加。原先流经主翼下表面的很少部分流体流向主翼上表面，流经襟翼缝道的流体减少，襟翼上表面前缘附近绕流的流速减小，这对应襟翼吸力峰值的稍微减小，襟翼下表面的压力分布基本没有变化，因此襟翼升力减小。

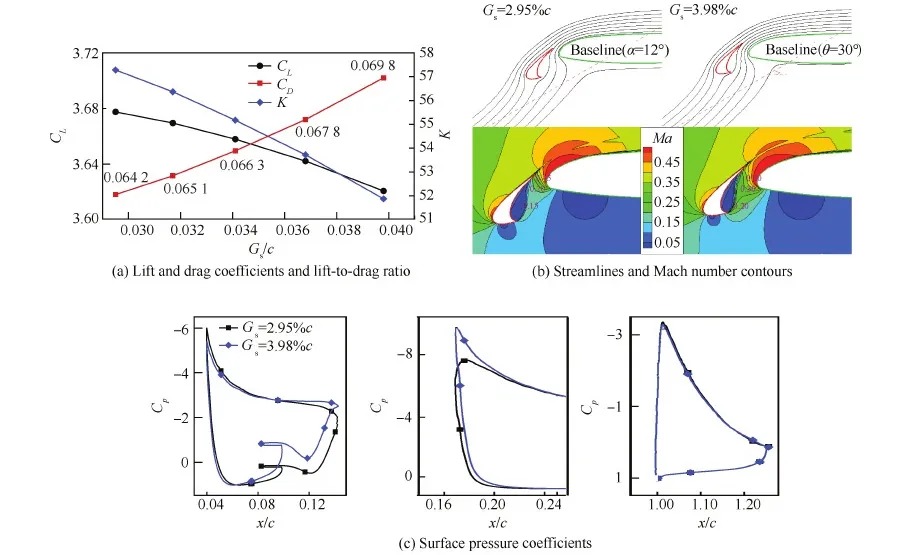
图6 不同缝道宽度基本构型在α=12° 下的计算结果 Fig.6 Calculation results of baseline configurations with different slat gap (α=12°)

这些计算结果表明Gs对多段翼型的气动性能具有重要影响，合适的Gs能提高总升力、降低总阻力和提高总升阻比。以上计算结果和结论与Renukumar等[20]对三段翼型前缘缝翼和后缘襟翼缝道参数的影响研究所得结论一致，这也从另一个方面反映了数值方法的可靠性。在上述计算的不同Gs的基本构型中，最小Gs=2.95%c构型的气动性能最优，而最大Gs=3.98%c构型的气动性能最差。

3.2 前缘缝翼微型后缘装置的影响

在以上不同Gs基本构型的前缘缝翼上布置图1 定义的MTED，对其附近网格进行适当加密，在研究局部网格敏感性的基础上进行对比计算。对于不同Gs情形，计算结果表明相同高度的MTED对各个翼段的影响定性一致，其中Gs=3.98%c情形的变化最大，下面将以它为例进行分析。

图7为Gs=3.98%c构型有/无高度为h=0.50%c的MTED的力和力矩系数的比较，对比图5与图7(两图中对应子图的坐标尺度相同)，MTED对前缘缝翼升力系数、后缘襟翼升力系数和总升力系数的影响，与减小Gs的影响在定性上是一致的；而在定量上它产生的变化较大，相对基本构型，MTED构型的总升力系数约增加6.98%。但它对主翼升力系数、总阻力系数和总力矩系数的影响与减小Gs的影响略有不同，表现为：MTED构型主翼线性段的升力线斜率以及整个计算迎角范围内的升力系数小于基本构型；它的总阻力系数在α=0° 时与基本构型相当，但随着迎角的增加它较快地增加而且逐步大于基本构型；总力矩系数的不同源于各个翼段升力变化的程度不同。

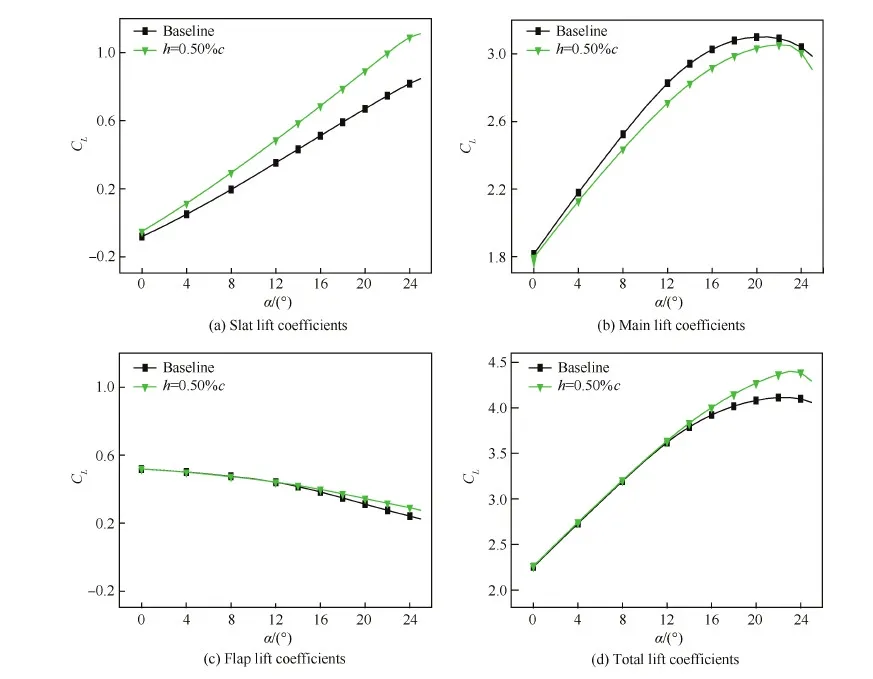
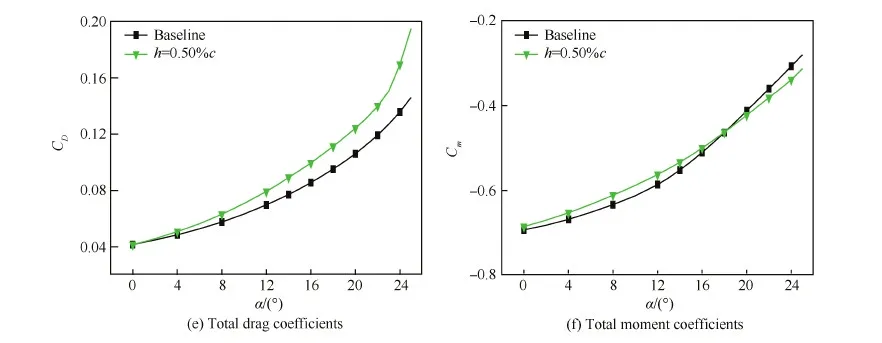
图7 Gs=3.98%c构型有/无前缘缝翼MTED的力和力矩系数(h=0.50%c) Fig.7 Coefficients of force and moment for Gs=3.98%c configuration with and without slat MTED (h=0.50%c)

图8为α=12° 时Gs=3.98%c基本构型和MTED构型的流线和马赫数云图以及表面压力分布。如图8(a)所示，与减小Gs类似的是流经MTED构型缝翼缝道的流体减小。在MT-ED之前和之后分别存在一个驻涡和一对反向涡，MTED构型整个缝翼上表面的流速加快，缝翼下表面、缝翼缝道和主翼上表面前缘附近的流速减慢。各个翼段的表面压力分布如图8(b)所示，MTED的“弯度效应”使缝翼后缘出现一个较大的后加载，同时缝翼吸力峰值增加，缝翼升力增加。这使缝翼的下洗效应增强，流经缝道的流线向主翼上表面的下偏程度增加，主翼吸力峰值受到抑制，整个主翼上表面的吸力都减小，因此主翼升力减小。襟翼受缝翼、主翼尾迹和襟翼缝道流动的综合影响，相比前两个翼段它的压力分布变化很小。总升力主要受缝翼和主翼的影响，缝翼升力的增量大于主翼升力的减量，因此总升力增加。

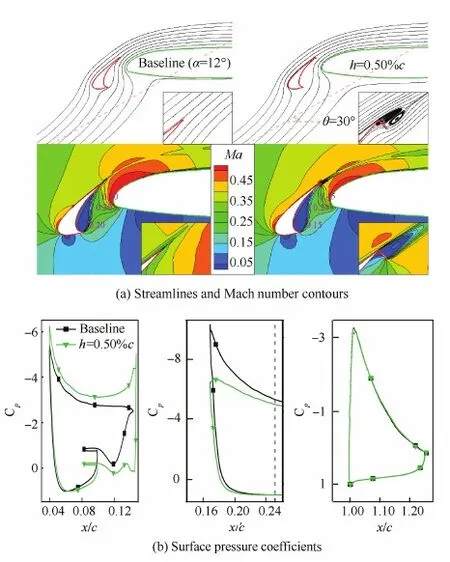
图8 α=12° 时Gs=3.98%c构型有/无前缘缝翼MTED的计算结果(h=0.50%c) Fig.8 Calculation results of Gs=3.98%c configurations with and without slat MTED at α=12° (h=0.50%c)

3.3 不同缝道宽度前缘微型装置构型的比较

对于基本构型，如图5(d)所示，当缝翼缝道宽度Gs从2.95%c增加至3.98%c时，α≤8° 的线性段升力系数变化不明显，但随着迎角的进一步增加升力线斜率逐渐减小，失速迎角提前，最大总升力系数约减小4.61%，这说明基本构型的气动性能对Gs比较敏感。

当不同Gs基本构型增加高度为h=0.25%c或0.50%c的前缘缝翼MTED时，两种高度的MTED构型随Gs变化的计算结果定性一致，与基本构型类似的是中间3个Gs构型的计算结果介于最小和最大Gs构型之间。图9为不同Gs情形两种高度MTED构型的计算结果比较，对比图9(a)与图5(d)，h=0.50%c的MTED构型总升力系数对Gs的敏感性明显降低，特别是在失速迎角附近的区域。在几个典型迎角下MTED构型的总升力系数随Gs的变化关系ΔCL如表2和图9(b)所示，αCLmax为最大升力系数CLmax下的迎角值。随Gs的增加h=0.50%c的MTED构型的总升力系数变化都相对很小，实际上各个翼段升力系数的变化也是如此，限于篇幅没有给出这些比较结果。图9(c)和图9(d)分别为MTED构型的最大总升力系数和失速迎角随Gs的变化曲线，h=0.50%c的MTED构型的失速迎角(在失速迎角附近计算迎角的间隔为1°)和最大总升力系数都逐渐趋于稳定值。

图9 不同缝道宽度情形MTED构型计算结果比较 Fig.9 Comparison of calculation results for MTED configurations with different slat gap

表2 总升力系数随缝道宽度的变化Table 2 Total lift coefficients vs slat gap

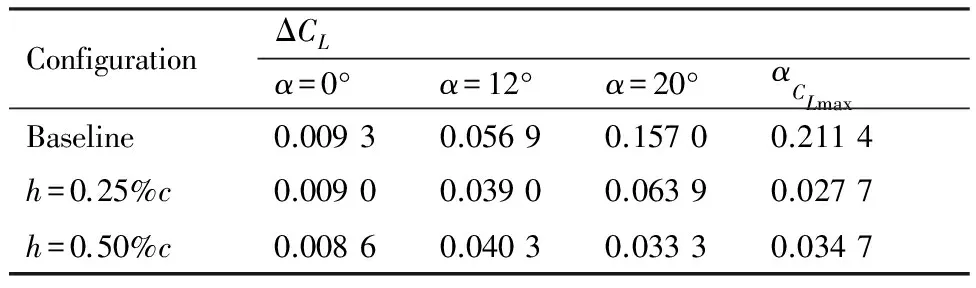
ConfigurationΔCLα=0°α=12°α=20°αCLmaxBaseline0．00930．05690．15700．2114h=0．25%c0．00900．03900．06390．0277h=0．50%c0．00860．04030．03330．0347

此外，对于同一缝翼缝道宽度Gs，两个不同高度h=0.25%c和0.50%c的MTED对各个翼段升力系数的变化虽然存在差异，但两者各自引起的失速迎角之前的总升力系数以及最大总升力系数的变化非常接近，后者的失速迎角小于前者。

4 结 论

1) 多段翼型基本构型的气动性能对缝翼缝道宽度Gs较为敏感，合适的Gs能有效改善多段翼型的失速性能和延迟失速迎角，在相同迎角下具有提高总升力系数、降低总阻力系数以及提高总升阻力的作用。

2) 前缘缝翼MTED改变了实际的缝翼缝道参数，其中主要减小了Gs，缝道宽度的改变本身会对多段翼型的气动性能产生一定的影响，但这个变化不起主导作用。

3) 前缘缝翼MTED的定性作用是：增加了缝翼后缘的弯度效应，使缝翼升力增加；抑制了主翼吸力峰值，使主翼升力减小；基本上不影响襟翼升力。由于缝翼升力增量大于主翼升力减量，因此总升力增加；它同时增加了总阻力，并通过各个翼段不同升力变化程度的综合作用影响总力矩的变化。

4) 前缘缝翼MTED对多段翼型气动性能的定量影响取决于前缘缝翼缝道参数，它对失速区域的影响明显大于线性区域，能够有效延长升力曲线的线性段和明显提高最大总升力系数，对失速迎角的影响还与它的高度有关。

5) 前缘缝翼MTED能够显著改善多段翼型基本构型的总升力系数对Gs较为敏感的特性，尤其是在失速区域，当缝翼缝道宽度Gs在一定范围内变化时可以保证总升力系数在一个较小的范围内变化。

6) 前缘缝翼MTED的高度在一定范围内时，它对多段翼型气动性能的影响相差很小，即它的高度敏感性不是很强。

[1] 李丽雅. 大型飞机增升装置技术发展综述[J]. 航空科学与技术, 2015, 26(5): 1-10.

LI L Y. Review of high-lift device technology development on large aircrafts[J]. Aeronautical Science and Technology, 2015, 26(5): 1-10 (in Chinese).

[2] VAN DAM C P. The aerodynamic design of multi-element high-lift systems for transport airplanes[J]. Progress in Aerospace Sciences, 2002, 38(2): 101-144.

[3] WANG X L, WANG F X, LI Y L. Aerodynamic characteristics of high-lift devices with downward deflection of spoiler[J]. Journal of Aircraft, 2011, 48(2): 730-735.

[4] ROSS J C, STORMS B L, CARRANNANTO P G. Lift-enhancing tabs on multielement airfoils[J]. Journal of Aircraft, 1995, 32(3): 649-655.

[5] 褚胡冰, 张彬乾, 陈迎春, 等. 微型后缘装置增升效率及几何参数影响研究[J]. 航空学报, 2012, 33(3): 381-389.

CHU H B, ZHANG B Q, CHEN Y C, et al. Investigation on mini-TED efficiency and impact of its geometrical parameters[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 381-389 (in Chinese).

[6] LIN J C, ROBINSON S K, MCGHEE R J, et al. Separation control on high Reynolds number multi-element airfoils[C]//10th Applied Aerodynamics Conference. Reston: AIAA, 1992.

[7] MELTON L P, YAO C S, SEIFERT A. Application of excitation from multiple locations on a simplified high-lift system[C]//2nd AIAA Flow Control Conference. Reston: AIAA, 2004.

[8] LITTLE J, NISHIHARA M, ADAMOVICH I, et al. Separation control from the flap of a high-lift airfoil using DBD plasma actuators[C]//4th Flow Control Conference. Reston: AIAA, 2008.

[9] HOLL T, ALEXANDER K, GIACOPINELLI P. Detached-eddy simulation of pulsed blowing actuation on the flap of a high-lift configuration[C]//29th AIAA Applied Aerodynamics Conference. Reston: AIAA, 2011.

[10] PAPADAKIS M, MYOSE R Y, MATALLANA S. Experimental investigation of Gurney flaps on a two-element general aviation, airfoil[C]//35th Aerospace Sciences Meeting & Exhibit. Reston: AIAA, 1997.

[11] CARRANNANTO P G, STORMS B L, ROSS J C, et al. Navier-Stokes analysis of lift-enhancing tabs on multi-element airfoils[J]. Aircraft Design, 1998, 1(3): 145-158.

[12] 周瑞兴, 高永卫, 金承信, 等. 具有Gurney襟翼的多段翼型空气动力特性分析[J]. 空气动力学学报, 2002, 20(2): 174-178.

ZHOU R X, GAO Y W, JIN C X, et al. The analyses of aerodynamic characters of multi-element airfoil with Gurney flap[J]. Acta Aerodynamica Sinica, 2002, 20(2): 174-178 (in Chinese).

[13] RUMSEY C L, YING S X. Prediction of high lift: Review of present CFD capability[J]. Progress in Aerospace Sciences, 2002, 38(2): 145-180.

[14] KLAUSMEYER S M, LIN J C. Comparative results from a CFD challenge over a 2D three-element high-lift airfoil: NASA-TM-112858[R]. Washington， D.C.: NASA, 1997.

[15] CHIN V D, PETERS D W, SPAID F W, et al. Flowfield measurements about a multi-element airfoil at high Reynolds numbers: AIAA-1993-3137[R]. Reston: AIAA, 1993.

[16] VALAREZO W O, DOMINIK C J, MCGHEE R J, et al. High Reynolds number configuration development of a high-lift airfoil[R]. Paris： AGARD, 1992.

[17] PETROSINO F, MINGIONE G, CAROZZA A, et al. Ice accretion model on multi-element airfoil[J]. Journal of Aircraft, 2011, 48(6): 1913-1920.

[18] TYAN M, PARK J, KIM S, et al. Subsonic airfoil and flap hybrid optimization using multi-fidelity aerodynamic analysis: AIAA-2012-5453[R]. Reston: AIAA, 2012.

[19] 王运涛, 孟德虹, 邓小刚. 多段翼型高精度数值模拟技术研究[J]. 空气动力学学报, 2013, 31(1): 88-93.

WANG Y T, MENG D H, DENG X G. High-order numerical study of complex flow over multi-element airfoil[J]. Acta Aerodynamica Sinica, 2013, 31(1): 88-93 (in Chinese).

[20] RENUKUMAR B, BRAMKAMP F D, HESSE M, et al. Effect of flap and slat riggings on 2-D high-lift aerodynamics[J]. Journal of Aircraft, 2006, 43(5): 1259-1271.

(责任编辑： 李明敏)

URL：www.cnki.net/kcms/detail/11.1929.V.20170217.1322.006.html

Passiveflowcontrolofmulti-elementairfoilsusingslatmini-trailingedgedevice

ZHANGZhenhui,LIDong*,YANGYin

NationalKeyLaboratoryofScienceandTechnologyonAerodynamicDesignandResearch,NorthwesternPolytechnicalUniversity,Xi’an710072,China

BasedontheMcDonnellDouglasAerospacethree-elementhighliftconfiguration,two-dimensionalunsteadyReynoldsaveragedNavier-Stokesequationstogetherwithshearstresstransport(SST)k-ωturbulencemodelareemployedonthemulti-blockstructuredgridofC-Htypetoinvestigateapplicationofslatmini-trailingedgedevice(MTED)topassiveflowcontrolofmulti-elementairfoils.ConsideringthattheactualslatslotparameterswouldbechangedduetoadditionofslatMTED,effectsoftheslatgap,astheprimaryparametricvariation,ontheaerodynamiccharacteristicsofthestudiedthree-elementairfoilareinvestigated.Theresultsshowthatthemaximumtotalliftcoefficientisreducedbyabout4.61%whentheslatgapincreasesfrom2.95%cto3.98%c.ThesameslatMTEDpresentsqualitativelyconsistentimpactsonindividualelementsofthesebasicconfigurationswithdifferentslatgaps,namelyincreasingslatlift,decreasingmain-elementliftandalmostnegligibleeffectsonflaplift.Thecombinationoftheseliftchangesleadstoveryslightchangeinthelinearregionofthetotalliftcoefficient,butmoresignificantvariationdependingontheslatgapinthestallregion.Whentheslatgapis3.98%c,themaximumtotalliftcoefficientincreasesbyabout6.98%fortheconfigurationwiththeslatMTEDheightbeing0.50%c.

multi-elementairfoil;passiveflowcontrol;slat;mini-trailingedgedevice(MTED);slatgap

2016-07-27；Revised2016-12-12；Accepted2017-01-19；Publishedonline2017-02-171322

s：NationalNaturalScienceFoundationofChina(11072200)；MARSProjectCo-FundedbyEuropeanUnionandChineseMIIT

.E-mailldgh@nwpu.edu.cn

2016-07-27；退修日期2016-12-12；录用日期2017-01-19； < class="emphasis_bold">网络出版时间

时间：2017-02-171322

www.cnki.net/kcms/detail/11.1929.V.20170217.1322.006.html

国家自然科学基金 (11072200)； 中欧国际合作项目MARS

.E-mailldgh@nwpu.edu.cn

张振辉， 李栋， 杨茵． 基于前缘缝翼微型后缘装置的多段翼型被动流动控制J． 航空学报,2017,38(5):120650.ZHANGZH,LID,YANGY.Passiveflowcontrolofmulti-elementairfoilsusingslatmini-trailingedgedeviceJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120650.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.120650

V211.3

A

1000-6893(2017)05-120650-11