用于直升机在大气紊流中的旋翼状态反馈控制

吉洪蕾， 陈仁良， 李攀

南京航空航天大学 航空宇航学院 直升机旋翼动力学国家级重点实验室， 南京 210016

用于直升机在大气紊流中的旋翼状态反馈控制

吉洪蕾， 陈仁良*， 李攀

南京航空航天大学 航空宇航学院 直升机旋翼动力学国家级重点实验室， 南京 210016

发展了一种集成旋翼状态反馈(Rotor-State Feedback, RSF)控制的飞行控制系统，以提升直升机在大气紊流环境中低速飞行时的飞行品质。基于经典显模型跟踪控制系统，对机体和旋翼状态反馈增益进行协同设计，以综合优化旋翼/机体耦合动稳定性和直升机在飞行品质相关频率范围(1～12 rad/s)内的紊流缓和能力。同时，设计了一个旋翼前馈控制以增强直升机的操纵响应特性。对直升机飞行品质的线性分析表明：RSF控制的引入能够在实现旋翼/机体耦合动稳定性控制的同时使滚转和俯仰通道的指令跟踪延迟时间分别降低21.87%和25.82%，扰动抑制带宽分别提升243.22% 和72.56%。最后以飞行试验验证的高阶非线性飞行动力学模型进行数值模拟验证控制系统。结果表明：RSF控制的引入使直升机滚转、俯仰角速率对紊流响应的标准差分别降低55.68%和26.81%。集成RSF的控制系统能够提升直升机在紊流中的飞行品质。

直升机； 大气紊流； 飞行品质； 旋翼状态反馈； 模型跟踪控制； 飞行动力学

直升机低空、低速的飞行特点使其经常工作在具有强紊流的环境中。大气紊流会严重恶化直升机的飞行品质、导致操纵困难甚至驾驶员诱发振荡，威胁飞行安全。因此必须采取措施提升直升机在大气紊流中的飞行品质。

传统的基于机体状态反馈的飞行控制系统通过增大反馈增益能够提升直升机的紊流缓和能力并改善操纵特性，但过大的反馈增益会导致旋翼/机体耦合振荡、乃至不稳定[1-2]。因此，许多研究人员[3-5]提出采用旋翼状态反馈(Rotor-State Feedback, RSF)增加旋翼模态的稳定性并增大机体状态反馈增益以提升飞行品质。

Chen等[6-7]结合理论分析与飞行试验结果研究了旋翼等高阶动力学系统对高带宽飞行控制设计的影响，并采用一个高阶线性直升机飞行动力学模型分析RSF对直升机飞行动力学特性的提升能力。研究表明旋翼等高阶系统是限制直升机反馈增益的主要因素，采用RSF控制可以辅助控制系统实现更高的带宽，且能够提升直升机阵风扰动抑制能力。同一时期，Takahashi[8-9]采用黑鹰直升机悬停状态的一个高阶线性模型分析了机体/旋翼状态反馈在实现高带宽飞行控制系统中的作用。结果表明，在控制系统中引入RSF能够有效提升旋翼模态的稳定性从而获得更高的机体状态反馈增益，提升直升机的操纵品质、降低控制系统对传感器噪声的灵敏度。除了上述理论分析，Howitt等[10-11]采用试验方法评估了RSF在控制系统中的作用。试验基于一个缩比旋翼模型，不同形式的RSF被引入到控制系统中进行评估。试验结果表明，RSF能够保证后退型挥舞模态的稳定性，从而可以采用更大的机体状态反馈增益实现高带宽控制系统设计。最近，Horn等[12]设计了一个可以无缝整合到既有控制系统中并且可随时断开的RSF控制器，以消除在之前研究中发现的旋翼转速变化所导致的旋翼/机体耦合振荡现象[13]，确保在旋翼转速变化时仍然能够保持较高的操纵带宽和稳定性。

上文所述研究的焦点在于获得更大的机体状态反馈增益以提升直升机操纵带宽及扰动抑制能力，RSF主要用来稳定由于高机体状态反馈增益导致的旋翼/机体耦合不稳定模态。对在强紊流环境中飞行的直升机，在控制系统中引入RSF的另外一个好处却鲜有考虑：旋翼既是直升机的主要操纵面也是紊流扰动产生的重要源头之一，引入RSF能够增强对旋翼的控制，缓和旋翼对紊流的扰动响应。本文提出对旋翼/机体状态反馈增益进行协同设计，以综合优化旋翼/机体耦合动稳定性和直升机在飞行品质相关频率范围内(1～12 rad/s)的紊流缓和能力。同时，设计了一个旋翼前馈控制以提升直升机的操纵响应特性。然后将设计的RSF控制律整合到已有的经典显模型跟踪控制系统。以一个高阶线性飞行动力学模型分析RSF对直升机稳定性、操纵响应以及紊流缓和能力的影响，并以一个经过飞行试验验证的高阶非线性飞行动力学模型进行数值模拟验证所设计的控制系统。

1 飞行动力学模型

本文通过对已有的高阶非线性飞行动力学模型[14-16]进行线化获得线性模型。模型所选用的机型为黑鹰直升机，建模相关的参数见文献[14]，模型验证见文献[15-16]。

整个模型共21个运动自由度，包含机体的6个刚体运动自由度、旋翼各片桨叶的挥舞、摆振和1个弹性扭转自由度、动态入流的3个自由度、尾桨入流的1个自由度、机身的1个侧洗和下洗自由度。模型的状态空间形式为

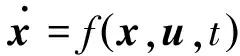
(1)

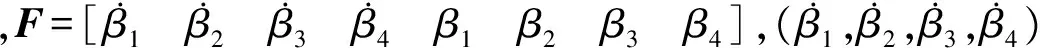
2 大气紊流模型

采用一种三维空间大气紊流模型[16]进行直升机在紊流中的非线性飞行模拟。详细的大气紊流模拟及直升机各部件处紊流扰动速度的计算方法见文献[16]。将紊流速度分量叠加到直升机各气动部件的迎角、侧滑角和动压计算项中以考虑紊流对直升机的影响。包含紊流速度项的直升机飞行动力学方程形式为

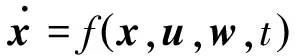
(2)

式中：

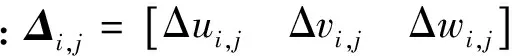
3 控制系统设计

本文以经典显模型跟踪控制系统[17-19]为基础设计旋翼状态反馈控制，并集成到原控制系统中。下文首先简要介绍显模型跟踪控制系统，然后介绍旋翼状态反馈控制设计方法。

3.1 显模型跟踪控制

图1 显模型跟踪控制系统结构图 Fig.1 Architecture of explicit model-following control system

图1所示为本文采用的经典显模型跟踪控制系统结构，由3个部分组成：指令模型M(s)、被控对象逆模型P-1(s)和反馈补偿模块H(s)，s为拉普拉斯算子。图中：us为驾驶杆输入操纵量；xcom为指令模型输出状态量；uff为逆模型输出操纵量；ufd为反馈补偿模块输出操纵量；ua为作动器操纵量；P(s)为被控对象即直升机；x为被控对象输出状态量。

由图1可知，如果被控对象Ps的理想逆模型P-1s存在，则整个系统的传递函数为

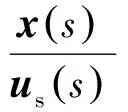
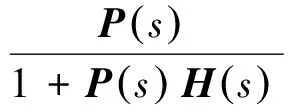
(3)

即系统与指令模型等价，消除了直升机的动力学特性，被控对象输出x完全等于指令模型输出xcom。因此，只需给出合适的指令模型即可满足提出的设计要求。

指令模型，又被称为显模型，是直升机的指令输出，也是控制系统需要跟踪的目标。指令模型的设计以现行的直升机飞行品质规范为依据，同时还应该考虑到与被控对象的匹配，例如假如选择的指令模型带宽过大，使直升机难以跟踪指令模型，会导致系统飞行品质下降。理想的直升机角速率响应具有一阶特性，姿态响应具有二阶特性。本文所关注的为直升机滚转、俯仰通道的姿态指令/姿态保持(Attitude Command/Attitude Hold,ACAH)响应类型[20]，以俯仰通道为例，以二阶传递函数表示其指令模型为

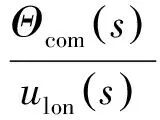
(4)

逆模型对被控对象进行前向补偿，提高直升机对操纵的响应速度。理想的逆模型的零点与被控对象的极点对消，能够消除被控对象的动态特性。旋翼和作动器等具有高频动力学特性部件的动态特性是不可能消除的，重心偏离等低频动力学特性的影响可以由反馈补偿模块抑制。因此，对直升机刚体运动的传递函数进行拟合获得的一阶或二阶模型足以满足控制系统对逆模型的要求。以俯仰通道为例，其拟合的低阶等价模型可以一阶传递函数表示为

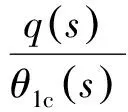
(5)

式中：Kq和Tq分别为低阶等价模型的增益和时间常数。

反馈补偿模块的作用是稳定直升机各运动模态、抑制干扰，使被控对象能够稳定地跟踪指令模型输出。Tischler等[18]指出对于高带宽控制系统，较高的反馈增益能够抑制处于低频段的飞行动力学模态，系统的带宽主要由旋翼等具有高频动力学特性的部件决定。

从上文描述可知，为获得高带宽显模型跟踪控制系统，指令模型应与控制系统对指令模型的跟踪能力协调。如果对指令模型的跟踪能力不足，则会导致控制系统无法及时跟踪指令模型输出，恶化直升机的操纵响应特性。为定量描述控制系统对指令模型的跟踪能力，定义指令跟踪延迟时间为

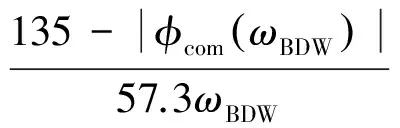
(6)

式中：τmf为指令跟踪延迟时间；ωBDW为根据飞行品质规范[20]确定的系统带宽频率；φcomωBDW为指令模型在带宽频率ωBDW处的相位角。

3.2 旋翼状态反馈控制

在经典显模型跟踪控制系统的基础上，设计RSF控制器，以增强旋翼/机体耦合模态的动稳定性，增大机体状态反馈增益，并提升旋翼对紊流的缓和能力。RSF控制器通过反馈纵、横向周期挥舞、摆振角和角速率，获得纵、横向操纵并叠加到显模型跟踪控制系统的作动器操纵输入中，如图2所示，其中da为扰动输入。研究表明旋翼纵、横向周期挥舞、摆振角和角速率可以提供充足的旋翼状态信息，使RSF控制拥有足够的鲁棒性[8,12]。同时，协同旋翼状态反馈设计，重新设计俯仰、滚转通道的反馈增益以提升直升机俯仰、滚转通道的飞行品质。

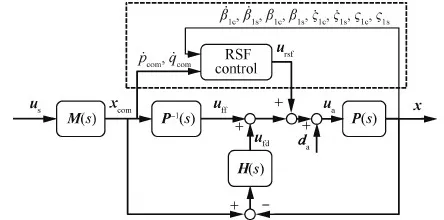
图2 集成旋翼状态反馈(RSF)的控制系统结构图 Fig.2 Architecture of control system integrated with rotor-state feedback (RSF)

由于挥舞、摆振运动的锥度角和无反作用角以及机体速度对旋翼周期挥舞、摆振运动以及机体俯仰、滚转运动的影响不大，假定它们与俯仰和滚转动力学解耦，得到机体姿态/旋翼状态耦合的动力学方程为

(7)

以式(7)的机体/旋翼动力学耦合模型为基础，采用线性二次型状态调节器(Linear Quadratic Regulator, LQR)最优控制方法[21]协同设计滚转、俯仰角及角速率反馈增益和旋翼状态反馈增益。该方法首先给出一个二次型性能指标，然后寻找最优状态反馈量使受扰偏离平衡位置的状态量在恢复到平衡位置附近的过程中性能指标最小，最终完成控制设计。本文采用如式(8)所示的性能指标求解LQR增益。

(8)

式中：权重系数矩阵Qb用来加权直升机俯仰、滚转角和角速率以避免过量的机体运动；矩阵Qf用来加权旋翼周期挥舞角，以避免过量的旋翼运动；矩阵R用来加权旋翼周期变距操纵，以避免控制器产生过大的操纵量。由于纵横向周期挥舞角直接影响直升机俯仰和滚转运动，因此将纵横向周期挥舞角计入性能指标，以提升直升机在高频范围内的紊流缓和能力。

依据极小值原理[21]，使式(8)中性能指标最小的最优控制存在且唯一，即

u*t=-R-1BTSxt=-Kxt

(9)

式中：K=R-1BTS为LQR状态反馈增益矩阵，S为正定对称矩阵，且满足式(10)所示的矩阵代数黎卡提方程。

-SA-ATS+SBR-1BTS-Q=0

(10)

式中：

(11)

由于LQR最优控制方法能够在获得最优解的同时确保闭环系统稳定并留有足够的幅值和相位裕度。因此，采用该方法对旋翼/机体状态反馈增益进行协同设计可以综合优化旋翼/机体耦合动稳定性和飞行控制系统的紊流缓和能力。

机体和旋翼状态反馈增益的取值随加权矩阵Qb和Qf的增大而增大，使直升机紊流缓和能力随之增大。然而由于受到作动器权限以及滤波器等高阶系统延迟时间的限制，LQR增益不能取值过大。通过反复尝试，选择各加权矩阵

(12)

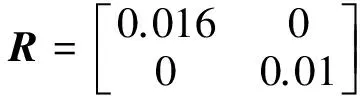
(13)

引入RSF会降低旋翼的操纵灵敏度，从而降低控制系统对指令模型的跟踪能力，如图3所示。因此本文采用一个前馈控制增强对指令模型的跟踪能力，最终的RSF控制系统结构如图4所示。由于纵、横向周期挥舞角是影响直升机滚转、俯仰运动的主要因素，因此滚转和俯仰的动力学特性可近似表示为

(14)

(15)

图3 RSF对控制系统指令跟踪能力的影响 Fig.3 Effect of RSF on command tracking capability of control system

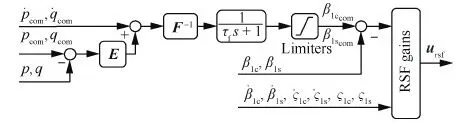
图4 旋翼状态反馈控制结构图 Fig.4 Architecture of RSF control

增加旋翼前馈控制的目的是增强对指令模型的跟踪能力，不应该加快旋翼的响应致使引发过量的超调，因此，在前馈回路中增加一个惯性环节以软化旋翼指令输入，其时间常数τf约等于旋翼响应的时间常数。

4 飞行品质分析

基于高阶线性飞行动力学模型，分别对经典显模型跟踪控制系统(Baseline Explicit Model-Following Control System)和集成RSF控制系统的稳定性、操纵响应特性和紊流缓和能力进行分析，研究RSF控制对直升机低速飞行品质的影响。经典显模型跟踪控制系统的反馈系数取自文献[18]。指令模型的参数综合考虑直升机本身性能以及飞行品质规范ADS-33E-PRF[20]的要求得出，如表1所示。

表1 指令模型参数Table 1 Parameters of command model

4.1 稳定性

图5和图6所示为有无RSF时旋翼/机体耦合模态对滚转角速率和滚转角反馈的根轨迹图，滚转角速率反馈增益变化范围为0～150(%·rad-1·s)，滚转角反馈增益变化范围为0～1 000(%·rad-1)，计算状态为前飞速度为20 m/s，箭头表示旋翼/机体耦合模态随反馈增益增大的变化方向。

从图5中可以看出，随着滚转角速率反馈增益的增大，挥舞模态的固有频率增大，阻尼较小的摆振后退型和前进型模态则逐渐变得不稳定。这是因为直升机的横向操纵是通过改变旋翼的横向挥舞角实现的，并且在小速度时由机体产生的滚转阻尼可以忽略不计，滚转角速率反馈的引入相当于对旋翼横向周期挥舞角施加积分反馈控制，导致旋翼挥舞运动模态的固有频率增加，阻尼比减小，旋翼挥舞角速率响应增大；随着滚转角速率反馈增益的增加，逐渐增大的挥舞角速率响应导致在摆振平面内由旋翼旋转产生的科氏力逐渐增大，最终导致本身阻尼较小的摆振模态发散。

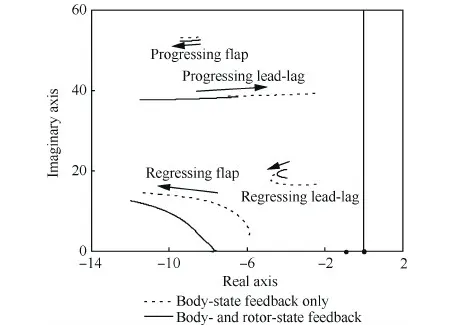
图5 旋翼/机体耦合模态对滚转角速率反馈根轨迹图 Fig.5 Root locus of rotor/body coupling modes with roll rate feedback

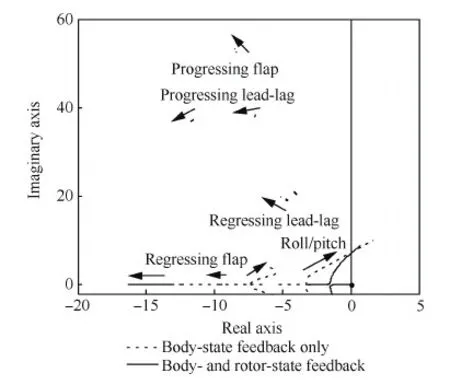
图6 旋翼/机体耦合模态对滚转角反馈根轨迹图 Fig.6 Root locus of rotor/body coupling modes with roll angle feedback

从图6中可以看出，滚转角反馈对旋翼模态动稳定性的影响较小，这是因为滚转角运动的固有频率远低于旋翼各模态的固有频率。由于小速度飞行时机体产生的滚转阻尼可以忽略不计，滚转

角反馈的引入相当于对滚转角速率施加积分控制，因此随着滚转角反馈增益增大，滚转角速率的阻尼减小，最终导致滚转/俯仰角速率耦合模态发散。

另外，从图5和图6中可以看出RSF的引入使旋翼/机体耦合模态的根轨迹要么整体向复平面的左侧移动了一段距离，要么减缓了其随滚转角速率和滚转角反馈增益增大向复平面右侧偏移的趋势，增强了旋翼/机体耦合模态的动稳定性，使控制系统能够采用更大的机体状态反馈增益。这是因为RSF控制能够增加旋翼挥舞和摆振运动的阻尼，从而使系统更加稳定。

经典显模型跟踪控制系统和本文发展的集成RSF控制系统的旋翼/机体耦合模态动稳定性和直升机频域稳定裕度分别见表2和表3。从表中可以看出，集成RSF的控制系统能够保证旋翼/机体耦合模态的动稳定性，具有与经典显模型跟踪控制系统同等程度的稳定裕度，但是前者的相位和幅值穿越频率更大，这使系统拥有更强的指令跟踪能力和紊流缓和能力，见表3及下文分析。因此，本文提出的基于LQR理论的旋翼/机体状态反馈增益协同设计方法能够实现旋翼/机体耦合动稳定性控制和飞行控制的综合优化。

表2 旋翼/机体耦合模态固有频率和阻尼比Table 2 Natural frequencies and damping ratios of rotor/body coupling modes

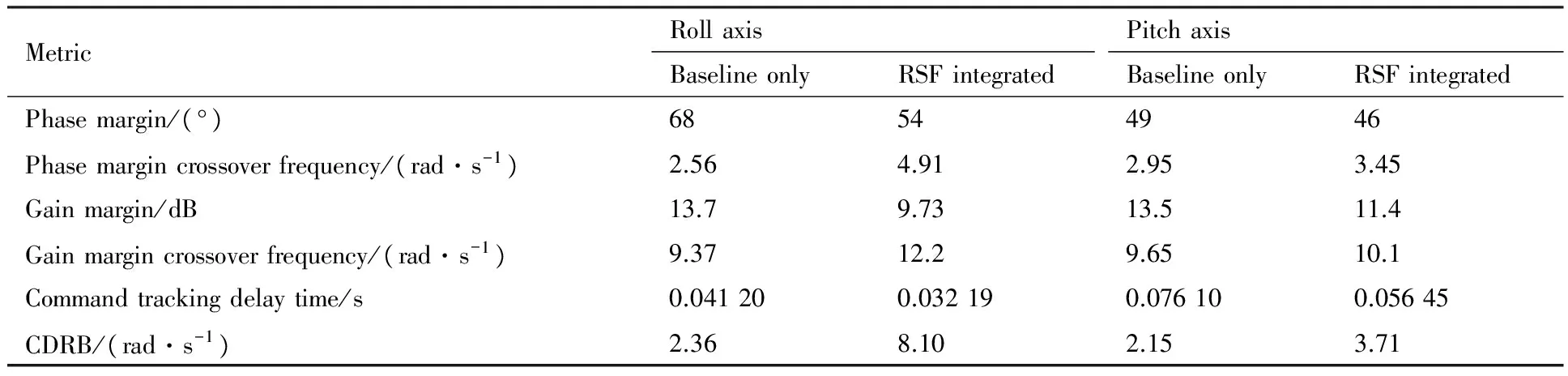
表3 控制系统线性评估结果Table 3 Linear evaluation of control systems

Note: CDRB—Control Equivalent Disturbance Rejection Bandwidth.

4.2 操纵响应特性

图7所示为20 m/s前飞时俯仰角对纵向操纵的传递函数Bode图，作为对比，指令模型的Bode图也被绘制在图中。从图中可以看出，与经典显模型跟踪控制相比，RSF控制的引入使系统能够以更小的相位延迟跟踪指令模型，从而具有更好的操纵响应特性。这是因为RSF控制的引入增强了旋翼/机体耦合模态的动稳定性，从而能够采用更大的机体状态反馈增益，增强系统对指令模型的跟踪能力。同时，上文所设计的旋翼前馈控制也增强了旋翼对指令模型的跟踪能力。

图7 俯仰角对纵向操纵输入传递函数的Bode图 Fig.7 Bode plots of transfer functions from longitudinal input to pitch angle

经典显模型跟踪控制系统和集成RSF控制系统的指令跟踪延迟时间见表3。与经典显模型跟踪系统相比，RSF控制的引入使滚转、俯仰通道的指令跟踪延迟时间分别降低了21.87%和25.82%，显著提升了系统的指令跟踪能力，具有进一步增加指令模型带宽从而增强直升机操纵响应特性的潜力。

4.3 紊流缓和能力

控制系统的紊流缓和能力由作动器扰动输入da到作动器总输出ua之间的闭环传递函数ua(s)/da(s)度量，如图2所示。其中，

(16)

由式(16)可知，增大系统反馈增益Hs可以提升系统的紊流缓和能力。与经典显模型跟踪控制系统相比，集成RSF的控制系统可以采用更大的机体状态反馈增益，因此可以提升系统在低频范围内的紊流缓和能力。又因为RSF的引入提高了旋翼和直升机在高频范围内的紊流缓和能力，因此，集成RSF的控制系统能够提高直升机在整个飞行品质相关频率范围内(1～12 rad/s)的紊流缓和能力，如图8所示。其中飞行速度为20 m/s。

采用Link等[22]提出的操纵等效扰动抑制带(Control Equivalent Disturbance Rejection Bandwidth, CDRB)定量评估直升机紊流缓和能力。CDRB是指当作动器扰动输入da到作动器总输出ua之间的闭环传递函数ua(s)/da(s)的幅频特性上升到-3 dB时的频率，如图8所示。20 m/s前飞时经典显模型跟控制系统和集成RSF控制系统的CDRB见表3。与经典显模型跟踪控制系统相比，集成RSF的控制系统对滚转、俯仰通道的CDRB分别提升243.22%和72.56%。

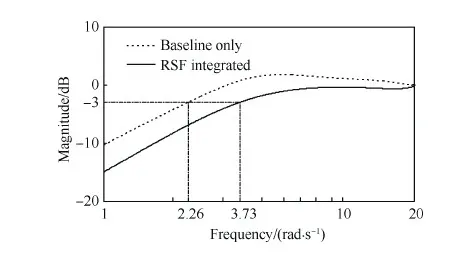
图8 俯仰通道紊流缓和传递函数的Bode图 Fig.8 Bode plots of transfer functions for turbulence alleviation of pitch axis

5 非线性数值模拟

分别将经典显模型跟踪控制系统和集成RSF的控制系统接入式(2)的高阶非线性飞行动力学模型，进行直升机在大气紊流中的操纵响应数值模拟，分析RSF控制对直升机在紊流环境中飞行品质的影响。在模拟计算中采用多桨叶坐标变换方法[23]将飞行动力学模型输出的单片桨叶挥舞、摆振状态量转换到不旋转坐标系，然后输出给RSF控制系统。

图9所示为直升机在大气紊流环境中对10%纵向偶极方波操纵的响应时间历程。响应计算的初始状态为在30 m高空以20 m/s的前飞速度进行稳定平飞，垂向大气紊流强度为2 m/s。图9(a)～图9(d)为机体滚转、俯仰角和角速率的响应时间历程。从图中可以看出，2种飞行控制系统都能够使直升机在大气紊流环境中进行机动操作时保持良好的稳定性，但是与经典显模型跟踪控制系统相比，集成RSF的控制系统对指令输出的跟踪误差更小，对紊流的缓和能力更强。图9(e)～图9(f)为对应的周期挥舞角时间历程，可以看出，集成RSF的控制系统显著提升了旋翼本身的紊流缓和能力。最后，以直升机滚转、俯仰角速率对紊流扰动响应的标准差定量评估RSF对直升机紊流缓和能力的提升，如表4所示。从表中可以看出，RSF的引入使直升机滚转、俯仰角速率对紊流响应的标准差分别减小55.68%和26.81%。

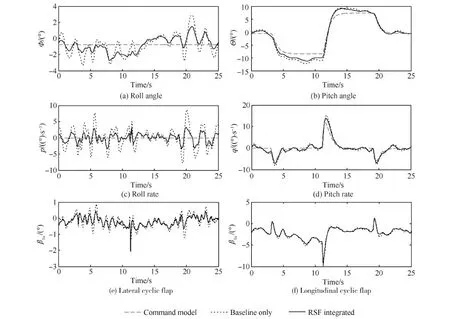
图9 直升机对10%纵向偶极方波操纵的响应时间历程 Fig.9 Time histories of helicopter response to 10% doublet in longitudinal input

表4 直升机角速率对紊流扰动响应的标准差

Table4Standarddeviationofhelicopterangularrateresponsestoturbulence

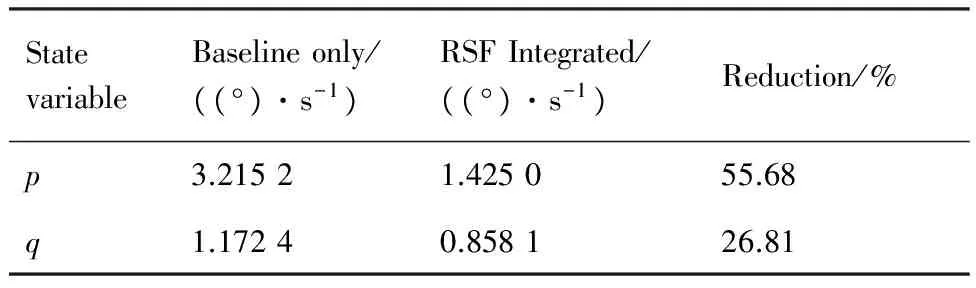
StatevariableBaselineonly/((°)·s-1)RSFIntegrated/((°)·s-1)Reduction/%p3．21521．425055．68q1．17240．858126．81

6 结 论

基于经典显模型跟踪控制系统，本文发展了一种集成RSF控制的飞行控制系统。提出对旋翼/机体状态反馈增益进行协同设计，以实现旋翼/机体耦合动稳定性控制与飞行控制的综合优化，提升旋翼和机体的紊流缓和能力，提高直升机在大气紊流中的飞行品质。通过以上分析可以得到以下结论：

1) RSF能够增加旋翼/机体耦合模态的动稳定性，有助于获得更高的机体状态反馈增益，但会降低原控制系统对指令模型的跟踪能力，需要增加适当的前馈控制以补偿控制系统对指令模型的跟踪能力。

2) 线性分析表明，本文提出的RSF控制方法能够实现旋翼/机体耦合动稳定性控制和飞行控制系统的综合优化，增大机体状态反馈增益并增强对旋翼的控制，使滚转和俯仰通道的指令跟踪延迟时间分别降低21.87%和25.82%，扰动抑制带宽分别提高243.22%和72.56%。

3) 非线性数值模拟表明，RSF的引入使直升机滚转、俯仰角速率对紊流响应的标准差分别降低55.68%和26.81%。本文设计的集成RSF控制系统能够增强直升机在大气紊流环境中的操纵响应特性，提升机体和旋翼的紊流缓和能力，提高直升机在大气紊流中的飞行品质。

[1] DRYFOOS J B, KOTHMANN B D, MAYO J. An approach to reducing rotor-body coupled roll oscillations on the RAH-66 Comanche using modified roll rate feedback[C]//American Helicopter Society 55th Annual Forum. Fairfax, VA: American Helicopter Society, 1999: 1-14.

[2] FLETCHER J W, LUSARDI J, MANSUR M H, et al. UH-60M upgrade fly-by-wire flight control risk reduction using the RASCAL JUH-60A in-flight simulator[C]//American Helicopter Society 64th Annual Forum. Fairfax, VA: American Helicopter Society, 2008: 1-26.

[3] ELLIS C W. Effects of rotor dynamics on helicopter automatic control system requirements[J]. Aeronautical Engineering Review, 1953, 12(7): 30-38.

[4] HALL W E, BRYSON A E. Inclusion of rotor dynamics in controller design for helicopters[J]. Journal of Aircraft, 1973, 10(4): 200-206.

[5] BRICZINSKI S, COOPER D. Flight investigation of rotor/vehicle state feedback: NASA CR-132546[R]. Washington, D.C.: NASA, 1975.

[6] CHEN R T N, HINDSON W S. Influence of high-order dynamics on helicopter flight-control system bandwidth[J]. Journal of Guidance, Control, and Dynamics, 1986, 9(2): 190-197.

[7] CHEN R T N. An exploratory investigation of the flight dynamics effects of rotor RPM variations and rotor state feedback in hover: NASA-TM-103968[R]. Washington, D.C.: NASA, 1992.

[8] TAKAHASHI M. Rotor-state feedback in the design of flight control laws for a hovering helicopter[J]. Journal of the American Helicopter Society, 1994, 39(1): 50-62.

[9] TAKAHASHI M.H∞helicopter flight control law design with and without rotor state feedback[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1245-1251.

[10] HOWITT J, HOWELL S E, MCCALLUM A T, et al. Experimental evaluation of flight control system designs exploiting rotor state feedback[C]//American Helicopter Society 57th Annual Forum. Fairfax, VA: American Helicopter Society, 2001: 1-9.

[11] HOWITT J. Application of non-linear dynamic inversion to rotorcraft flight control[C]//American Helicopter Society 61th Annual Forum. Fairfax, VA: American Helicopter Society, 2005: 1-10.

[12] HORN J F, GUO W, OZDEMIR G T. Use of rotor state feedback to improve closed-loop stability and handling qualities[J]. Journal of the American Helicopter Society, 2012, 57(2): 1-10.

[13] GUO W, HORN J F. Rotor state feedback control for rotorcraft with variable rotor speed[C]//AIAA Guidance, Navigation, and Control Conference Proceedings. Reston: AIAA, 2009: 1-12.

[14] HOWLETT J J. UH-60A Black Hawk engineering simulation program: NASA CR-166309[R]. Washington, D.C.: NASA, 1981.

[15] 李攀, 陈仁良. 直升机急拉杆机动飞行仿真建模与验证[J]. 航空学报, 2010, 31(12): 2315-2323.

LI P, CHEN R L. Formulation and validation of a helicopter model for pull-up maneuver simulation[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(12): 2315-2323 (in Chinese).

[16] 吉洪蕾, 陈仁良, 李攀. 适用于直升机飞行力学分析的三维空间大气紊流模型[J]. 航空学报, 2014, 35(7): 1825-1835.

JI H L, CHEN R L, LI P. A model of three-dimensional-field atmospheric turbulence for helicopter flight dynamics analysis[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1825-1835 (in Chinese).

[17] LANDIS K H, GLUSMAN S I. Development of ADOCS controllers and control laws, Volume 2—Literature review and preliminary analysis: NASA CR-177339[R]. Washington, D.C.: NASA, 1987.

[18] TISCHLER M B, FLETCHER J W, MORRIS P M, et al. Flying quality analysis and flight evaluation of a highly augmented combat rotorcraft[J]. Journal of Guidance, Control, and Dynamics, 1991, 14(5): 954-963.

[19] FROST C R, HINDSON W S, MORALEZ E, et al. Design and testing of flight control laws on the RASCAL research helicopter[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit. Reston: AIAA, 2002: 1-11.

[20] United States Army Aviation and Missile Command, Aviation Engineering Directorate. Aeronautical design standard performance specification handling qualities requirements for military rotorcraft: ADS-33E-PRF[S]. Redstone Arsenal, AL: United States Army Aviation and Missile Command, Aviation Engineering Directorate, 2000: 6-21.

[21] 陈复扬. 自动控制原理[M]. 北京： 国防工业出版社, 2010: 433-438.

CHEN F Y. Principles of automatic control[M]. Beijing: National Defense Industry Press, 2010: 433-438 (in Chinese).

[22] LINK D W, KASHAWLIC B E, FUJIZAWA B T, et al. Influence of frequency response analysis on MH-47G DAFCS development and flight test[C]//American Helicopter Society 67th Annual Forum. Fairfax, VA: American Helicopter Society, 2011: 1-15.

[23] PADFIELD G D. Helicopter flight dynamics[M]. 2nd ed. Oxford: Blackwell, 2007: 102-108.

(责任编辑： 鲍亚平， 徐晓)

URL：www.cnki.net/kcms/detail/11.1929.V.20160913.0838.002.html

Rotor-statefeedbackcontrolforhelicopterinatmosphericturbulence

JIHonglei,CHENRenliang*,LIPan

NationalKeyLaboratoryofScienceandTechnologyonRotorcraftAeromechanics,CollegeofAerospaceEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

ThispaperdevelopsahelicopterflightcontrolsystemintegratedwithaRotor-StateFeedback(RSF)controllawtoimprovehelicopterflyingqualitiesatlowspeedinturbulentatmosphericenvironment.Basedonthebaselineexplicitmodel-followingcontrolsystem,thefeedbackgainsofthebodyandrotorstatesaredesignedinsynergyforcomprehensiveoptimizationofboththestabilityofthecouplingrotor/fuselagedynamicsandtheturbulencealleviationintheinterestedfrequencyrangeofflyingqualities(1-12rad/s).Meanwhile,afeed-forwardcompensationdesignisaddedtoimprovethehelicopterresponsivenesstopilotcontrols.AlinearanalysisofthehelicopterflyingqualitiesshowsthatwiththeintegrationoftheRSFcontrollaw,thestabilityofthecouplingrotor/fuselagedynamicscanbeensured,andthecommandtrackingdelaytimesofrollandpitchaxesarereducedby21.87%and25.82%respectively,aswellasthedisturbancerejectionbandwidthsareimprovedby243.22%and72.56%.Ahigh-ordernonlinearflightdynamicmodelvalidatedagainstflighttestdataisusedtoconductasimulationtoverifytheintegratedcontrolsystem.ResultsshowthatwiththeintegrationoftheRSFcontrollaw,thestandarddeviationofthehelicopterrollandpitchrateresponsestoatmosphericturbulencearereducedby55.68%and26.81%,respectively.TheflightcontrolsystemintegratedwiththeRSFcontrollawhasthecapabilitytoimprovehelicopterflyingqualitiesinatmosphericturbulence.

helicopter;atmosphericturbulence;flyingqualities;rotor-statefeedback;model-followingcontrol;flightdynamics

2016-06-17；Revised2016-07-28；Accepted2016-08-24；Publishedonline2016-09-130838

s：NationalNaturalScienceFoundationofChina(51405227,11672128)

.E-mailcrlae@nuaa.edu.cn

2016-06-17；退修日期2016-07-28；录用日期2016-08-24； < class="emphasis_bold">网络出版时间

时间：2016-09-130838

www.cnki.net/kcms/detail/11.1929.V.20160913.0838.002.html

国家自然科学基金 (51405227,11672128)

.E-mailcrlae@nuaa.edu.cn

吉洪蕾， 陈仁良， 李攀． 用于直升机在大气紊流中的旋翼状态反馈控制J． 航空学报,2017,38(5):120541.JIHL,CHENRL,LIP.Rotor-statefeedbackcontrolforhelicopterinatmosphericturbulenceJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120541.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0242

V212.4

A

1000-6893(2017)05-120541-10