基于贝叶斯分层模型的可违约债券利率期限结构

吴建华 张颖 王新军

(1.济南大学数学科学学院，山东 济南 250022；2.山东大学经济学院，山东 济南 250100)

引言与文献综述

无论是微观金融资产定价、金融风险管理和投资分析，还是宏观经济预测和货币政策制定，利率期限结构都发挥着极其重要的角色。国债收益率曲线从一个侧面反映了实体经济、金融市场的状况和市场主体对经济未来的预期信息。而可违约债券的利率期限结构则在风险管理中被用于推测企业债券的信用评级和评估衍生品的风险。因此，对于利率期限结构的准确估计和预测研究一直是学界和业界的热点问题。现代利率期限结构模型研究大致可以分为如下三类模型：经验估计模型(包括样条拟合模型和参数拟合模型)，仿射期限结构模型(包括均衡模型和无套利模型)和宏观-金融模型。以上这些研究方向都从不同的角度对利率期限结构展开了丰富的研究。最早利用统计学方法对利率期限结构进行经验估计的文献可以追溯到McCulloch and Huston(1971)[1]和McCulloch(1975)[2]，他们将贴现曲线模型化为多项式基础函数的一个线性组合，分别利用二次和三次多项式样条模型来拟合收益率曲线。在此基础上，Schaefer(1981)[3]提出了利用Bernstein多项式模型化收益率曲线的思路。不过多项式样条函数会引起远期利率的剧烈波动，为此Vasicek and Fong(1982)[4]提出指数样条模型，它可以有效避免远期利率的剧烈波动，获得更为平滑的远期收益率曲线。类似的，Shea(1984)[5]提出了B-样条模型，Fisher et al.(1995)[6]提出了平滑样条模型。以上这些方法主要采用分段曲线对收益率曲线进行拟合，因此被统称为样条类模型。另外一些学者采用了整段曲线对收益曲线进行拟合的思路，即所谓的参数化拟合模型，比如Nelson and Siegel(1987)[7]提出的Nelson-Siege模型，以及在NS模型基础上，Svennson(1994)[8]提出的Svennson模型。针对已有的这些参数模型，Bliss(1997)[9]提出了交叉效度方法检验这些模型的有效性。再后来，Diebold and Li(2002)[10]基于NS模型提出了动态NS(DNS)模型，估计了不同时刻刻画收益率曲线水平、斜率和曲度的三个因子。周子康等(2008)[25]提出了NSM模型，他们通过对指数多项式添加扩展项，调整了收益率曲线的形状，既保留了NS类模型的经济学含义和参数的稳健性，也克服了NS类模型的单峰特征。张蕊等(2009)[26]通过在DNS模型中引入第四个因子，建立了四因子的动态NS利率期限结构模型，利用Kalman滤波方法处理了非线性最优化问题。在模型的应用方面，王志强和康书隆(2010)[27]针对经典的NS模型在实际应用中存在部分久期配比免疫问题，提出利用收益率预期信息对模型进行动态调整的思路，从而改进了NS模型的应用。在模型的估计方面，De Rezende and Ferreira(2014)[11]提出了利用分位数回归估计扩展的Nelson-Siegel模型的方法。沈根祥和陈映洲(2015)[28]通过在DNS模型中引入新的斜率因子，从而构造了双斜率的DNS利率期限结构模型，提高了模型对短期收益率的静态拟合和动态预测绩效。尚玉皇等(2015)[29]通过对DNS模型进行扩展，构建一种混频Nelson-Siegel模型。张雪莹等(2017)[30]在Diebold et al.(2006)[12]提出的动态Nelson-Siegel模型中，通过引入政府债券的供给和需求变量，讨论了国债供求关系、利率期限结构与宏观经济变量之间的变动关系，构建了含有国债供求变量的动态Nelson-Siegel模型。目前这两类利率期限结构的经验估计方法已经被业界的Bloomberg和Reuters的电子信息系统所采用。

从模型拟合所采用的债券数据类别来看，以上的研究几乎都是基于政府债券数据来估计无风险利率的期限结构，相比而言，针对可违约债券利率的期限结构估计的研究相对较少。尤其是国内的相关研究更少，一个重要的原因就是，无论是从发行量还是从发行规模上来看，可违约债券都相对落后于发达的国债市场，从而相应的数据也较少，对于某些期限较长的可违约债券来说，发行数量更少。根据中国债券市场数据显示，2015年中国债券市场各券种未结清数量占比分别为政府债34.62%，银行债16.52%，公司和企业债5.12%，金融类企业短期融资券22.77%，其他债券20.97%。显然，相比政府债券，可违约债券(公司债和企业债)在未结清的数量方面相形见绌1。

从现有的文献来看，最早研究企业债券的利率期限结构估计的是Schwartz(1998)[13]，他提出先用信用评级作为分类标准，将所有的企业债券划分成不同的组别，然后构建每一组内债券的利率和期限之间的变动关系。不过这种估计思路有一个较大的缺点：组内样本容量较小。这就使得对收益率曲线估计的精度较低，表现为曲线的平滑度较低。为了增加组内的样本容量，Houweling et al.(2001)[14]和Jankowitsch and Pichler(2002)[15]提出了对企业债券和政府债券的进行联合建模的思路，充分利用政府债券发行量较大的优点，以增加样本容量，这样针对每一个信用评级水平，都可以生成信用价差曲线的估计量，而且可以获得更为平滑的收益率曲线。Krishnan et al. (2010)[16]沿着Diebold and Li(2006)[10]提出的参数化方法，基于发行公司作为分类标准对债券进行分类，利用指数多项式来模型化价差曲线的差。在此基础上，Jarrow et al. (2012)[17]基于样条的模型将企业债务的期限结构描述为无风险期限结构和一个价差曲线的和，然后利用非线性最优对模型参数进行了估计。虽然后面这几个研究通过增加政府债券来提高样本的容量，从而改进了模型估计的精度，不过这仅仅是一种权宜之计，对于单纯估计可违约债券利率期限结构的研究，仍然有待进一步探索。为了克服可违约债券的利率期限结构估计中出现的某些组内样本数据较少的问题，本文提出了利用贝叶斯分层模型(Gelman et al. 2013)[18]对所有的分组进行联合估计的思路。贝叶斯分层模型在生物、心理学和教育学等社会学科中应用广泛，它特别适用于参数多于样本点的情形。从现有的研究来看，将贝叶斯分层模型引入到利率期限结构估计中的研究思路几乎还是一个空白，本文试图在这一方面进行探索。

本文首先在Svensson利率期限结构模型框架内，构建可违约债券价格的贝叶斯分层模型，并给出分层Dirichlet后验分布估计的MCMC算法的具体实现过程。其次，利用中国债券交易所市场的债券数据对贝叶斯分层模型和经典的单曲线模型进行了对比实证分析。最后，提出了贝叶斯分层模型在各种利率期限结构研究中的应用前景。

模型构建及其估计方法

债券的利率期限结构是指在相同的违约风险水平下，在某一时刻，不同的到期期限与对应的零息债券到期收益率之间的关系。债券利率期限结构的经验估计是指以零息债券的市场价格为基础，找到某个平滑函数来拟合某一时点的债券利率与不同期限之间的变动关系。不过市场上大多数债券都是附息债券，零息债券较少，因此需要通过某种方法从附息债券价格中推导出零息债券的到期收益率。基本的思路为：附息债券可以看作是一系列不同期限零息债券的组合，附息债券的价格应该等于复制其现金流量的所有零息债券的价值的总和。因此，可以用零息债券的利率期限结构来计算附息债券的价格。根据零息债券和附息债券的这种关系，可以利用实际市场中的付息债券的价格倒推出零息债券的利率期限结构。

一、拟合函数与权重的选择

考虑n只同等信用质量的附息债券，记tmi为第i只债券的到期日，其中i=1,2…,n，在债券有效期内需要多次支付现金流(利息或本金)C(i,j)，支付时刻为ti,j(＞t)，其中j=1,2…,mi，mi为第i只债券的最大支付次数。根据现金流贴现原则，第i只附息债券在当前时刻t的理论价格P(t,tmi)可以如下计算：

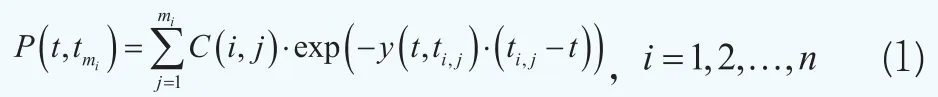
其中y(t,ti,j)表示第i只债券在时刻ti,j的到期收益率。假设g(t,ti,j;θ)为备选的近似函数，其中θ为待估计参数向量。那么P(t,tmi)的估计值为

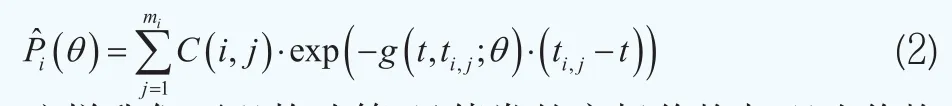
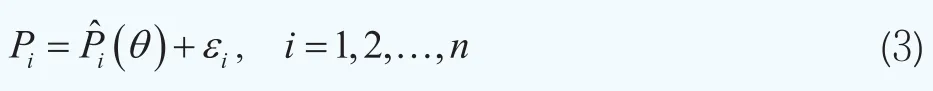
这样我们可以构造第i只债券的市场价格与理论价格之间的非线性回归模型其中Pi为第i只债券的市场价格，为债券的理论价格，εi是误差项，假设满足εi～N(0,τ-1)，其中τ为精度(逆方差)。在二次损失函数准则下，使得下面的目标函数最小时的参数向量即为待估计参数向量θ的最优值：

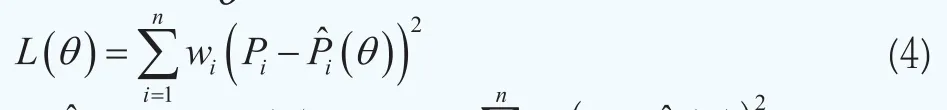
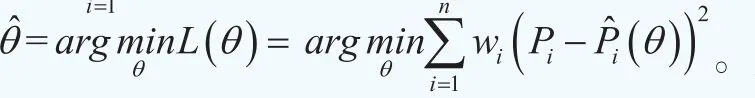
即其中Pi和分别为第i只债券在当前时刻t的市场价格和理论价格，wi为第i只债券在定价误差中所占的权重，引入权重的目的是对定价误差中的异方差进行调整，在后面我们会专门讨论如何基于久期构造权重指标。以上的估计思路可以称之为加权非线性最小二乘准则。显然，模型估计的关键点有两个：一是选择何种与期限T有关的参数函数g(t,T；θ)来近似收益率曲线y(t,T)；二是如何构造权重指标wi，i=1,2…, n。

本文选取g(t,T；θ)为Svensson(1994)[8]函数以对收益率曲线y(t,T)进行整体逼近，即：

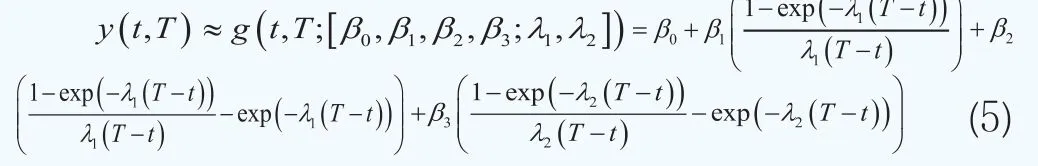
其中θ=(β0, β1, β2, β3)为形状系数，λ=(λ1, λ2)为缩减因子系数。Svensson函数是由Svensson(1994)[8]在Nelson-Siegel函数基础上提出的，它可以生成在实践中经常见到的一个较为宽泛的曲线的形状，曲线形状完全由四个参数所决定。β0刻画了利率的长期趋势，β1刻画了利率的短期行为，β2和β3描述了利率的中期行为，这两个参数共同决定了曲线的曲率和极值点的特征。这些参数使得利率期限结构的曲线更为灵活多变，它可以刻画水平型、单调型、V型、倒V型和驼峰型的曲线形状。

对于权重的选择。债券到期日的长短会影响到用于推测期限结构的信息量。基于久期综合了利率、期限和价格的信息可知，利率的变化对长期债券价格的影响要远大于对短期债券价格的影响。而在模型参数的估计中，最小化过程会减少定价误差的异方差，如果直接最小化误差平方和会导致长期收益率相对于短期收益率的过度拟合，从而降低收益率曲线短期部分的拟合效果。因此，在不考虑其他因素的情况下，应当对不同期限的债券赋予不同的权重。这样在最小化目标函数(4)中我们引入了一个权重wi，它表示第i只债券在定价误差中所占的比重，即

引入权重wi后，权重会按比例调整误差项的方差，即(τwi)-1。

接下来的问题就是如何量化权重wi。Bolder and Streliski(1999)[19]认为，既然债券的久期综合了到期收益率、价格和期限三者的信息，那么利用久期定义的权重可以将这些信息融合进估计的过程中。下面在不考虑其他因素的情况下，我们沿用该思路将第i个债券的权重定义为

其中Di为第i只债券的麦考利久期。麦考利久期是Macaulay(1938)[20]在全美经济研究局(NBER)的一次研究报告中提出的，它是利用债券现金流的现值作为权重的债券的到期日的加权平均值。具体的计算公式如下

其中Ci为t时刻需要支付的现金流，T为债券到期日，r为到期收益率。这样，在一组债券中，对于具有较短到期日的哪些债券来说，权重将趋于更高。

上面给出的利率期限结构估计的静态模型，可以用于政府和企业债券的期限结构的估计。在具体应用的时候，通常假设政府债券都有同样的期限结构。企业债券因为具有不同的违约风险水平，通常会根据某些分类准则将企业债券划分成不同的族群，然后对每一族群分别估计它们的期限结构。在实践中，一个流行的分类准则就是债券的信用评级。

二、利率期限结构的贝叶斯分层模型

在利用上述的单曲线估计方法对可违约债券进行估计时，经常会面临小样本问题，即在某些分组中，只有少数几只债券。这在债券市场上一个常见的现象，尤其在中国不发达的债券市场上这种问题更为严重。显然，在单曲线估计方法下，小样本问题会导致组内的估计精度会大幅度降低。为了克服小样本带来的估计精度较低的问题，本文提出了整体联合估计的贝叶斯分层模型的思路，通过对所有债券分组的期限结构进行联合建模，来抵消组内样本数量较少的问题，从而提高估计的精度。

实际上，在贝叶斯分析框架内估计利率期限结构模型的思路并不新鲜，Li and Yu (2005)[21]早就提出了在利用贝叶斯分析框架来估计利率期限结构模型的思路。不过从估计思路来看，他们的方法仍然属于单曲线估计方法，而本文则采用了多层先验分布和联合估计的方法思路。另外，他们利用样条函数来分段刻画收益率曲线，本文采用的是收益率曲线的参数函数整体拟合方法。

假设根据K个不同的信用级别把所有的企业债券划分成K组，这对应着需要估计K个不同的期限结构。令θK为刻画第k个期限结构的参数向量，那么需要对参数向量θ={θ1, θ2,…θK}进行估计。为了克服可能会出现的个别组内样本容量过小的问题，将参数向量θ设定多层先验分布，构建贝叶斯分层模型，这样就可以利用所有K组债券的信息对参数向量θ进行联合估计。

债券价格的贝叶斯分层模型主要包括下面的三个部分：

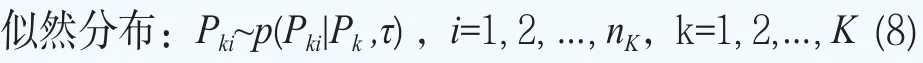
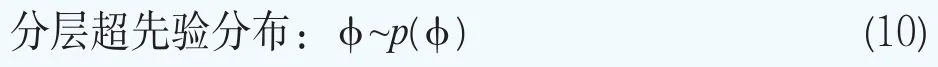
其中Pki为第k个分组中第i只债券的价格，其中i=1,2,…,nk，nk表示第k组中包含nk个债券，k=1, 2,…,K。

债券价格的似然函数分布P(Pki|θk ,τ)(i=1, 2,…,nk，k=1,2,…,K)由下面的非线性回归给出，即债券的市场价格被模型化为Pki=(θk)+εki，其中εki是误差项，假设满足εki～N(0,τ-1)，其中τ为精度(逆方差τ=1/σ2)。该式等价的概率模型为

其中P^i(θk)为第k组债券中的第i个债券的理论价格，根据式子(2)可知有如下形式

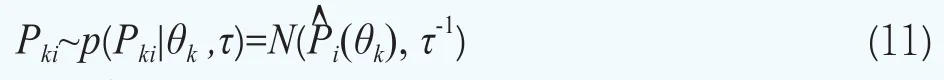
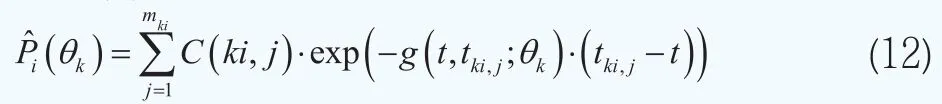
C(ki,j)为第k组债券中的第i个债券在时刻为tki,j(t＜ti,j＜mki)所支付的现金流(利息或本金)，j=1, 2,…,mki，mki为第i只债券的最大支付次数；g(t,tki,j；θk)被用于近似描述在时刻t的K个待估计的期限结构的第k个期限结构，这样每一个期限结构都通过一个四维向量θk=(βk0, βk1, βk2, βk3)来刻画。在上面的设定下，我们可以得到债券价格的似然函数p=(Pki|θkτ)(i=1, 2,…,nk，k=1, 2,…,K)。

为了估计模型参数θk，本文设计了一个有限混合先验分布，以保证模型能够捕获特定主体参数之间的异质性(包括异常点，超扩散点和多样态)。比如对于某些投资级的债券，由于某种原因导致这些债券的市场价格变得很低，这些债券应当被降级为垃圾级，如果这些债券的评级并没有及时发生改变，就会出现异常点。在数据概率建模中，对于数据的不同局部具有不同的变化特征时，单参数分布族无法给予确切地描述，但有限混合分布模型却能对其进行有效的刻画，而且有限混合分布模型具有良好的适应性和模拟性，它广泛的被应用于生物、基因工程、信息科学和金融保险等社会各领域。比如混合泊松分布在医学和保险精算领域有广泛应用；混合指数分布在信息工程领域里有一定应用；而正态混合分布应用更是广泛，理论证明任何有限分布都可以由等协差阵的有限正态混合分布任意逼近，而且正态混合分布模型也具有较高的灵活性和高效性的计算优势。关于正态混合分布更为详细的相关内容可以参考Yu and Deng(2015)[22]。

在贝叶斯分层模型中，将参数向量θk的先验分布设定为正态混合分布可以提高完全后验推断中的计算效率。我们用一个正态混合分布来模型化期限结构参数向量θk的分布p(θk|φ)，即

这样超参数可以写成φ={G}。贝叶斯模型的分层更多的是体现在对超参数φ={G}的分布的设定。下面沿用文献Müller and Quintana(2015)[23]的方法给出超参数φ={G}的超先验分布的设定。设G服从Dirichlet过程，即G～DP(G0，M)，其中基础分布G0服从多元正态分布，即G0～N(b，B)，它刻画了位置参数G的均值，M服从伽马分布和M～Ga(am，bm)，它决定了G围绕G0波动大小的程度。矩b和B被选择为与混合核是共轭的：b～N(b0，B0)和B-1～Wishart(r，(rW)-1)。对于精度τ，设定它服从伽马分布，即τ～Ga(aτ，bτ)。

综上所述，债券价格的贝叶斯分层模型如下给出：

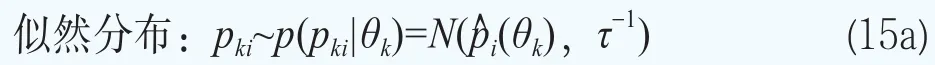
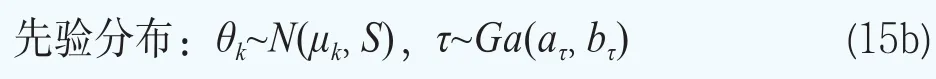
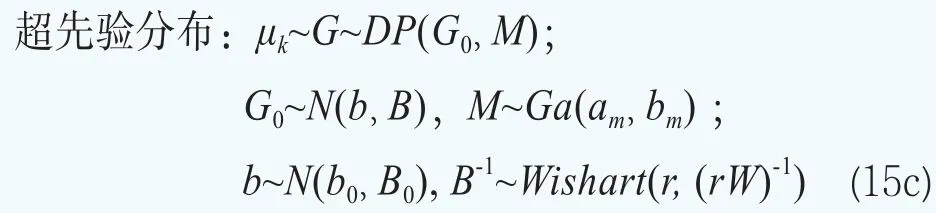
在本文设定的先验分布的超参数中，混合基础测度G0和协方差矩阵S对于所有的参数θk都是一样的。这样后验分布推断就可以利用所有期限结构共享的信息。

通过设定位置超参数G服从Dirichlet过程的先验分布，贝叶斯分层模型可以借用整个期限结构的力量，对每一个分组中的少数几个债券的期限结构进行联合建模，从而可以有效解决组内样本数量较少所带来的估计精度不足的问题。

显然，上面给出的贝叶斯分层模型的后验分布没有封闭解。利用MCMC算法从后验分布中进行抽样，可以获得参数的贝叶斯估计的近似解。令K为待估计的期限结构的个数，nk为期限结构k(k=1,2…,k)中的债券的个数。下面给出模型的MCMC算法。

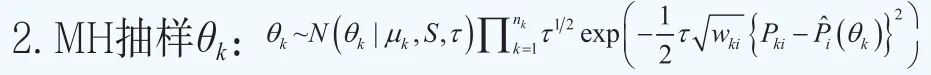
因为θk的后验分布没有封闭形式，需要利用Metropolis-Hasting算法更新θk。令θtk为第t次迭代时的当前点，θ*k为从替代分布q(θ*k|θtk)模拟的候选值。替代分布设为其中sd和ε为正的常数，t0是一个正整数，cov表示经验协方差矩阵。在本文中，我们令sd=0.5，ε=0.00001，t0=2000。该算法提供的适应性允许我们生成精确的估计量，即使我们对重要性分布的协方差矩阵设定了一个粗糙的近似。

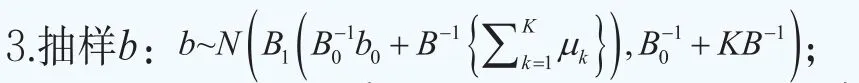
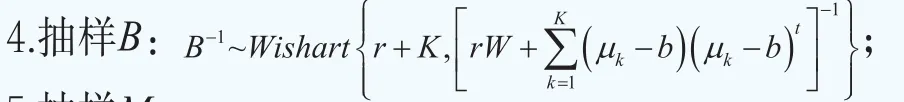
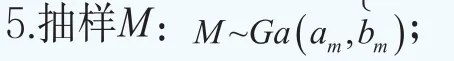
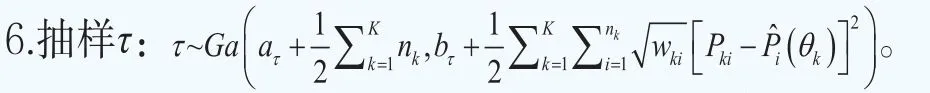
沿用文献Müller and Quintana(2004)的思路，对初始值和超参数做如下的设定。超参数为初始值为对于MH算法，为了对θk进行升级，我们设定其中和分别为参数θk的样本均值和样本协方差矩阵。

实证结果及分析

一、样本选取

本文所使用的数据是从和讯网债券债券行情抓取的2017年4月6日15∶00更新的交易所市场的债券交易数据，选取的变量主要包括：信用评级、本金、息票率、到期日、剩余年限、息票支付日、修正久期和最新报价。

债券样本的信用评级主要包括投资级债券(AAA,AA,A,BBB)，最大到期日为15年。我们排除了具有负的收益的所有债券，因为这些债券具有极差的流动性。最后样本数据集包含了国内248只未结清的企业债券的数据，基于信用评级的分类包括四组：AAA,AA,A和BBB；每一组中分别包括49、179、13和7只债券。

表1 基于信用评级的债券的分布情况

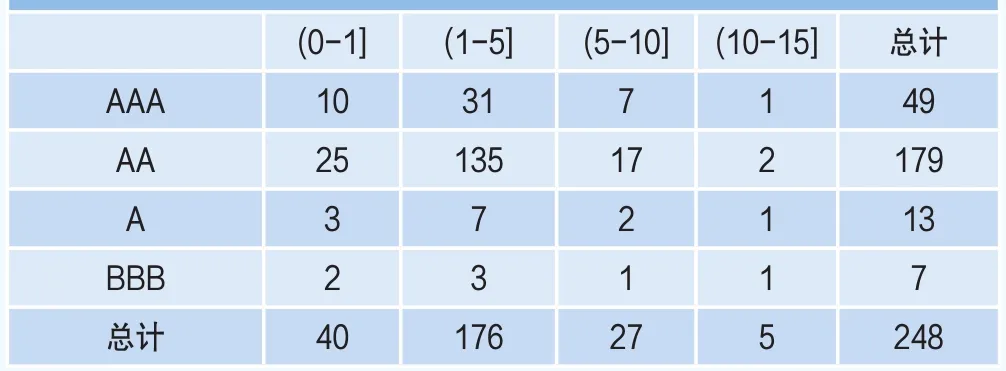
表2 基于剩余年限(列)和信用评级(行)的债券的分布情况

为了进一步考察到期日与债券个数的关系，表2给出了将剩余年限划分成了下面几组：

表2表明，债券的个数对于1年期以上的中长期债券来说，随着时间增长，债券的个数急速减少，比如，在剩余期限为1～5年的区间中有176只债券，它解释了样本中债券数量的71%。而在10以上的区间中，债券的个数只有1只。显然，剩余期限越短，债券的流动性越强，这可以部分的解释投资者对中短期债券更加偏好的流动性偏好理论。

本小节将上面的债券价格贝叶斯分层模型方法用于估计企业债券的期限结构。为了进行对比，本节也将利用单曲线方法对不同的期限结构进行估计。

二、实证结果及分析

1. 利率期限结构估计

单曲线方法利用现金流贴现原理估计得到基于信用评级的期限结构。在本文提出的利率期限结构的贝叶斯分层模型中，利用了作者自己编写的非线性似然函数程序，结合R软件包“DPpackage”和“termstrc”对模型进行了估计，软件包“DPpackage”专门针对贝叶斯非参数和半参数模型，利用模拟抽样技术从后验分布中抽样，其中的先验分布为服从Dirichlet过程的分层先验分布。本文通过最小化(4)中的加权平方误差来估计参数，权重由(6)定义，最优化问题利用了R软件中的nlminb()函数进行数值计算。

在利率的期限结构估计中，第k个期限结构的参数被估计为参数向量θk的后验均值，它由后验样本的平均值来近似。

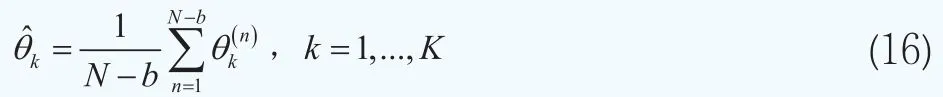
其中N为MCMC算法中的抽样迭代的次数，b为MCMC算法中的预烧期，K为期限结构的个数，在本文中K=4。对于精度参数τ也有类似的估计结构。

被估计的参数列在表3中，其中所有参数的马氏链路径最终都收敛在一定的区域里，波动比较平稳，且没有明显的周期性和趋势性。针对不同的信用级别，利用该方法都获得了相应的参数估计。利用可替代的初始值，在所有情形中的被估计参数都与表3中报告的数值基本一致。

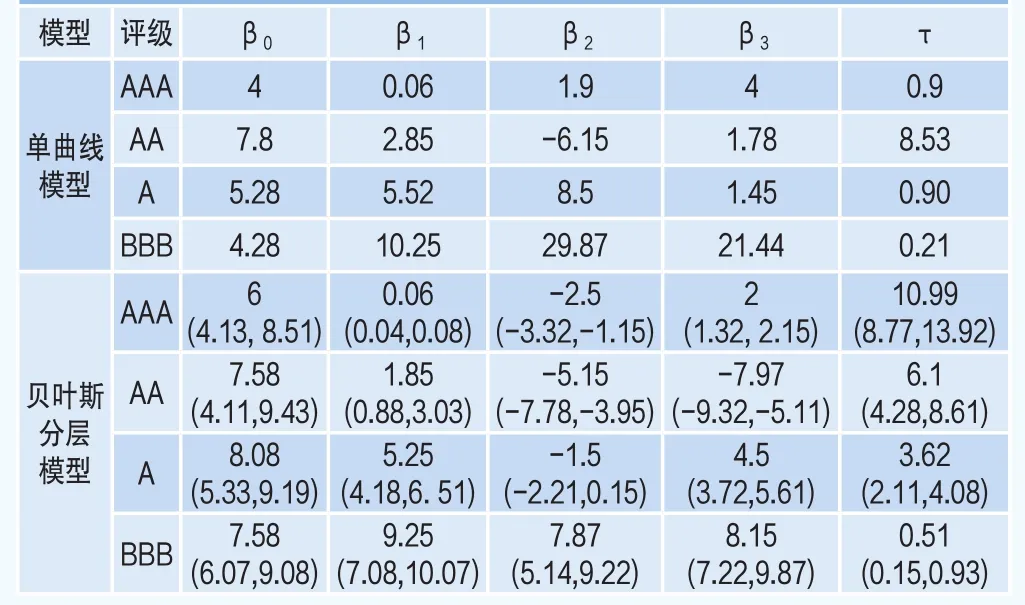
表3 基于信用评级分类的期限结构的被估计参数

为了进行对比，估计量的表达沿用了Nelson and Siegel(1987)[7]引入的原始参数化思路。对于利用贝叶斯分层模型获得的估计量，在括号中给出了估计量的90%的置信区间。

图1给出在四个不同的信用级别(AAA,AA,A,BBB)下的期限结构估计，给出了期限结构估计的单一曲线方法和贝叶斯分层模型估计。

从图1可以看出利用单曲线模型估计的利率期限结构时，AAA级和AA级表现出了较为合理的曲线形状，即到期日越长，收益率越高。但是A级和BBB级的收益率曲线表现出了与现实和理论不符的严重问题，比如A级和BBB级的收益率曲线不但表现出了不合理的隆起形状，甚至在长期，A级和BBB级收益率曲线竟然低于AA级的收益率曲线，这显然与信用级别越低，收益率越高的理论和现实相矛盾。如果探究其出现估计与现实出现较大偏差的原因，一个重要的原因就是，A级和BBB级的债券数据样本容量较小带来的估计偏差，比如A级债券的样本个数为13，BBB级债券的样本个数为7。

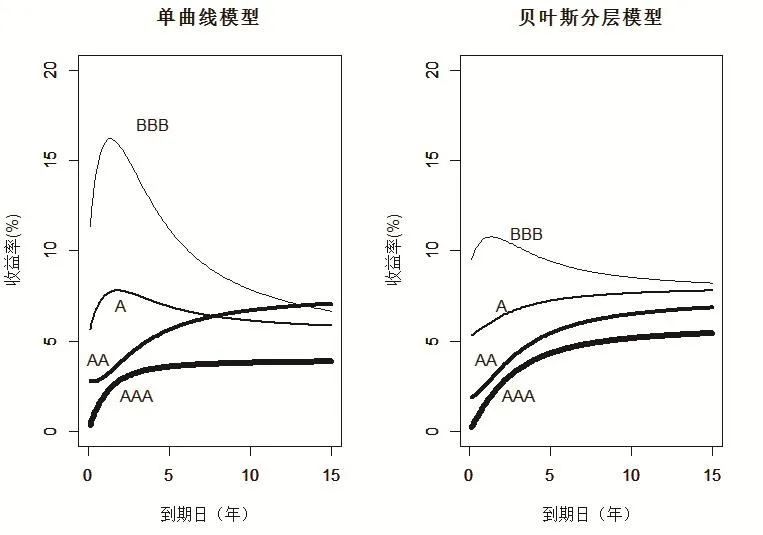
图1 基于信用评级分组的收益率曲线

相比而言，基于贝叶斯分层模型所估计的收益曲线则表现出了与现实和理论相一致的形状，它们的“顺序”与理论一致，这和信用风险和收益之间的预期关系是一致的：信用评级越低，收益越高。

从图1的对比可以证明，贝叶斯分层模型可以有效的克服个别分组内样本点过少所带来的估计精度偏低的缺点，而且估计结果现实，理论模型与流动性偏好理论基本一致，即投资者更加偏好短期债券，可以接受较低的收益率，而对于到期日较长的中长期债券，则会索取更高的收益率，以弥补可能发生的各种风险。

2. 模型估计的绩效分析

期限结构估计模型的绩效通过样本内和样本外预测作为标准进行对比。样本内的拟合优度根据价格残差(价格误差)进行度量，价格残差也叫价格误差，它等于市场价格减去债券的理论价格，理论价格由被估计的贴现曲线计算而得。对比价格残差是合适的，因为期限结构模型应该能够精确的解释市场价格，因为利率是债券价格的主要决定因素。具有最低价格误差的期限结构模型给出了最好的拟合。

样本预测绩效的计算利用了Steeley(2008)[24]提出的交叉效度分析。交叉效度的基本做法是，将数据集合划分成两个互补的子集训练集合和测试集合，首先利用训练集合来拟合期限结构，然后利用得到的期限结构计算测试集合中的每只债券的理论价格，接着根据市场价格算出价格残差，最后计算测试集合的根均方预测误差(RMSPE)和平均绝对预测误差(MAPE)见图2。

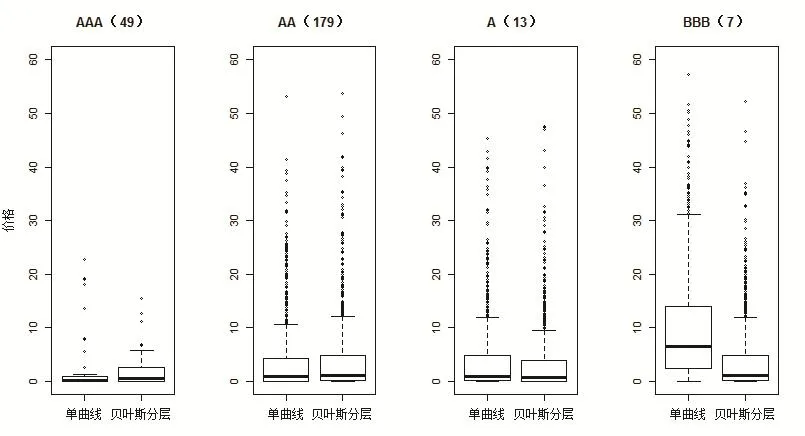
图2 单曲线和贝叶斯分层模型估计的样本内绝对价格误差

表4 平均RMSPE和MASPE

另外，在图2的箱线图和表5中，我们也给出了单曲线模型和贝叶斯分层模型估计的债券价格的样本预测绩效。

从图2和表4可以看出，贝叶斯分层模型和单一曲线估计量给出了价格估计的类似的样本内预测绩效。对于较低的信用评级，中位数和四分位数间距(IQR)都会上升。不过，贝叶斯分层模型的估计量的中位数绝对价格残差要小于单一曲线方法的残差。这说明，贝叶斯分层模型估计绩效要高于单曲线模型的估计绩效。

将分层贝叶斯模型用于基于信用评级的债券分组的期限结构的估计的最大好处是，由分层贝叶斯模型估计的收益曲线与经济理论相符。而且贝叶斯分层模型不会受到异常值的过度的影响：其中的DP先验分布允许异常值具有自己的聚集类，因此会独自离开主要的族群。通过将所有的债券保留在样本内，可以避免引入偏倚。

结论

本文探讨了如何利用贝叶斯分层模型估计可违约债券利率的期限结构的方法，通过对参数设定分层Dirichlet先验分布，可以对所有评级分组的参数进行联合估计，这样可以利用不同信用评级债券之间共享的信息，克服了单曲线模型面临的某些分组内的小样本所引起的估计精度较低的问题，从而可以基于小样本获得可靠的估计量。实证分析表明，在基于评级标准的债券分组中，期限结构的贝叶斯分层模型估计量比通过非线性加权最小二乘的单曲线估计量更加符合经济理论。而且贝叶斯分层模型在实践应用中可以较为容易的实施，模型参数不需要进行过多的调整。因为MCMC算法对初始值和固定超参数的设定极不敏感，在不同的初值设定下，给定足够大的迭代次数和合理的预烧期，总是可以获得稳健的、合理的估计结果。

本文提出的利率期限结构的贝叶斯分层模型也可以用于拟合基于其他分类标准的债券的期限结构。实际上，除了信用评级之外，也有一些影响债券期限结构的其他因素：流动性，税收和回收率等。将这些因素融期限结构估计的思路就是将它们也作为定义债券分类的标准。然而，以这些因素作为债券的分类标准，也会导致个别分组中的债券个数过小，利用本文的贝叶斯分层模型同样可以解决这个问题。

贝叶斯分层模型也是一个灵活的模型，它并没有被限定于仅仅估计特定类型的债券，比如该模型可以用于估计不同国家的债券之间的价差。我们可以将每一个国家看成是一类债券发行主体，然后联合估计他们的期限结构，之后将两个不同国家的估计曲线之间的差取为价差。此外，将企业或者政府债券与信用价差(企业债券和政府债券收益率之间的差)的估计进行结合，也可以利用贝叶斯分层模型方法。基于贝叶斯分层模型估计量的信用价差的计算可能会更加精确，因为在识别企业债券的潜在的期限结构方面，本文模型具有较好的绩效。

总之，本文探究的期限结构估计的贝叶斯分层模型能够在债券小样本数据下，获得期限结构更为精确的估计，它可以被广泛的应用于各种期限结构的估计，而不会受到样本容量的限制。

注释

1. 数据来源：中国债券信息网和《2015年债券市场统计分析报告》，中央结算公司研发部，2016 年1月4日。