基于Retinex算法对高阶全变差L1分解的实现∗

张鹏程

（河南广播电视大学 郑州 210098）

基于Retinex算法对高阶全变差L1分解的实现∗

张鹏程

（河南广播电视大学 郑州 210098）

在论文中我们提出了通过高阶总变异和L1分解的问题的反射率和照明分解模型。基于光照变化比反射光滑的观察，我们提出了一个凸变分模型，它可以通过一阶和二阶总变差有效地将图像的梯度场分解成凸边和相对平滑的照明场。所提出的模型可以通过Retinex方法有效地解决。在灰度和彩色图像上的数值实验显示了应用于图像恢复问题，实验显示算法可行有效。

Retinex算法；图像分解；高阶全变差；阴影校正

1 引言

在过去几十年里，对Retinex算法问题的研究激发了广泛的应用和讨论［1～3］。Retinex理论最初由Land和McCann提出作为人类颜色感知的模型视觉系统（HVS），其思想是HVS可以对其中照明和反射率都是未知的场的反射率进行校正［4］。我们的视觉系统往往看到与给定场景相同的颜色，而不考虑不同的照明条件。换句话说，它确保对象的颜色在变化的照明下保持相对恒定。最着名的Retinex问题之一是Adelson的棋盘阴影问题如图1所示，左侧是原始图像，右侧是问题图像。视觉上，图1的区域A似乎比区域B更暗，而数值上，这两个区域具有完全相同的强度值。这种现象是由不同的照明条件引起的，物体的感知强度是反射和照明的组合。

图1 Adelson原始图像

Retinex理论的主要目标是将给定图像I分解为两个分量［5～6］，即反射率 R 和光照 L

图2 Adelson的棋盘阴影问题

对于x∈Ω，其中Ω∈R2是图像的域。为了简化式（1），可以应用对数，假设R和L都是正数，因此

大多数分解方法是基于这个加性模型［7］。其中提出的primal-dual splitting算法是基于路径跟踪，并在进一步研究之后，路径跟随的想法被应用到变分模型中。在变分框架下，随后的总变差（TV）模型可以提取分段恒定反射率r与梯度场中的数据项［8］

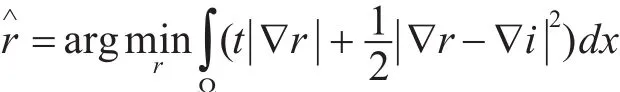
其中t＞0是权重参数。我们可以提出了一种更简单的基于L1的变分模型

δt(∇i)是相对于参数t的阈值梯度场。该模型在抑制测试的图像照明效果方面是有效的，然而，由于对图像梯度的量值的惩罚，也可以观察到反射率细节和对比度的损失。

同时对r和l进行惩罚的分解模型，提出了TV+H1分解模型［9］

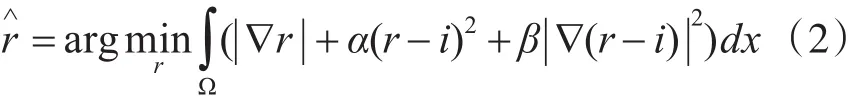
式（2）隐含地假设照明平滑和惩罚与H1范数。

在本文中，我们还考虑了同时恢复r和l的分解方法。特别地，我们使用高阶全变差提取照明l。在下面，我们提出一些相关的模型和符号。

众所周知，全变差正则化改善了所谓的楼梯伪影。为了克服这种效应，infimal卷积模型有很好的效果，infimal卷积模型被定义为

其中φ和Ψ是两个函数。

我们可以得到的一阶和二阶变量与权重的infimal卷积形式［10］

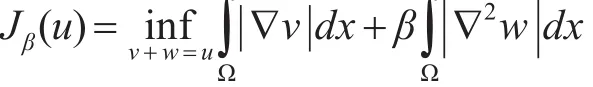
在更一般的双重公式中，定义了一阶和二阶全变差的非线性卷积模型

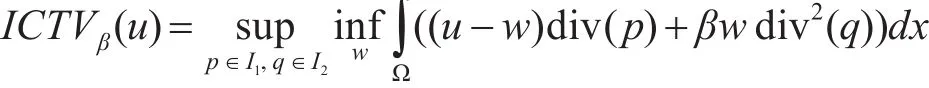
其 中I1={p ∈(Ω;R2)，‖p‖∞≤1}和I2={p ∈(Ω;R2×2)，‖p‖∞≤1}，如果考虑对称的Hessian矩阵，我们也可以定义I2={p ∈)，‖p‖∞≤1}，其中Sym2(R2)表示对称矩阵的空间。在这里，我们在(Ω;R2)和(Ω;Sym2(R2)使用 ‖ · ‖∞特别地，二阶TGV定义为

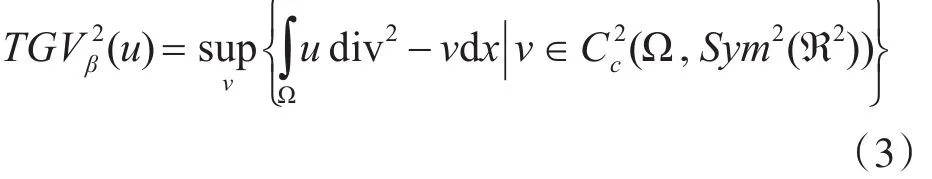
在简化形式中，式（3）可以写为

其中∇w∈R2×2是w∈R2的对称梯度。该公式也可以看作是用梯度场∇u=∇v+w的分解代替式（4）中的分解u=v+w。

2 高阶TV+H1分解模型

在这里，我们提出TV+H1变分模型的反射率和照明分解

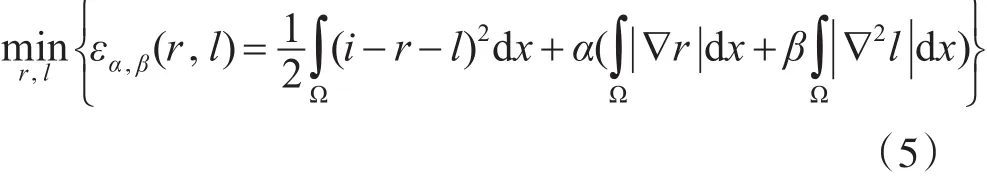
其中l表示照明度，r表示反射率，α＞0 ，β＞0是正则化参数。一般来说，我们在Retinex分解的梯度场中提取相对更平滑的分段线性分量为l，纹理部分为r。提出的模型可以等价为infimal卷积，令u=r+l，等于式（5）

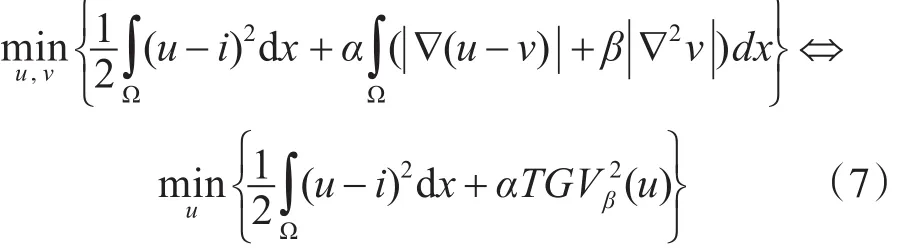
这里l没有明确给出，但它可以从数值方案中提取或通过解决泊松方程∇l=v的边界条件。模型（5）和infimal卷积模型（6），式（7）有一些缺点，如果我们感兴趣的r和l的解决方案。很容易看出，任何解对 (r +c， l -c)和c都是一个常数解，而这种非唯一性可能会极大地影响解的质量。此外，为了显示解的存在，需要理论的证明。因此，我们考虑模型（5）的展开，其对r和l的分量施加约束其中τ是很小的正数以确保l的有界性，Βr和Βl分别是r和l的约束。

3 Retinex算法

在本节中，我们提出了求解模型（8），在很多文献中也对其进行了研究［11～12］。例如广泛使用的split Bregman算法和Primal-Dual Splitting算法。这里，我们采用分裂不精确的Retinex算法，在我们对问题的求解迭代中。需要注意，两个未知数r，l在（8）中的耦合，因此，依次应用在内部交替方案中以求出关于r和l的子问题的完全解。

我们首先定义一些变量和方程来简化式（8）。

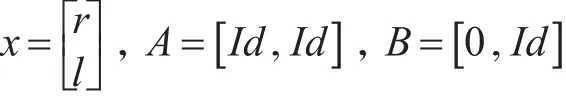
另外

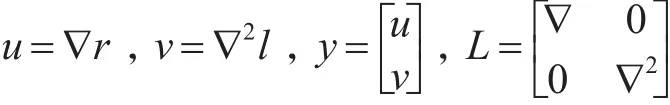
这里，我们使用向前差分和Neumann边界条件为离散梯度和对称化Hessian。在R2中，对于u∈W1，1(Ω)，我们有如下定义

作为对称的Hessian，在这里

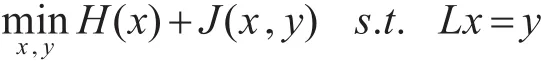
其拉格朗日公式为

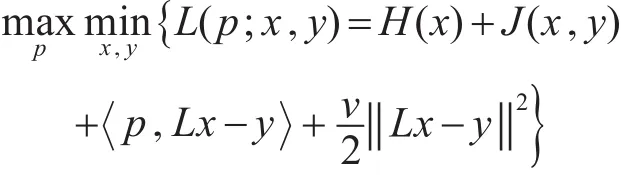
Retinex方法是交替方向法的一种不精确的变体的乘法器可有用于xk+1的更新问题，所以有以下迭代

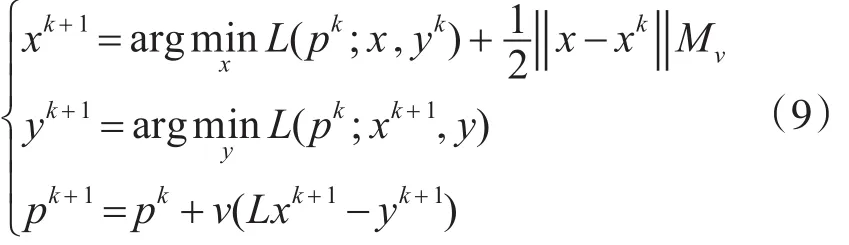
其中Mv是正定矩阵。为了获得一个比较容易的迭代方案，我们选择 Mv=Id-vLTL，其中0＜v＜1/‖‖LTL。

在下面，我们提出一个简单的派生方法分别更新xk+1和yk+1。

更新 xk+1：令 Mv=Id-vLTL

更新 yk+1：yk+11的更新也相当简单。因为‖‖y1，β=‖‖u1+β‖‖v1是可分的，我们有

所以我们得出以下两个简单的阈值步骤

最后，对于双变量 pk+1的更新是容易的。因此，结合式（9）、式（10）我们得到求解式（8）的迭代方案。

4 数值实验

上述棋盘阴影图像和Logvinenko的立方体阴影图像，如图2和图3所示。测试视网膜错觉。对于这两个图像，虽然视觉上区域B比区域A更亮，但是它们是的相同强度值。表1显示了两个方法处理之后测得两个区域强度的值。我们提出方法的对比其它的方法恢复图形的效果最佳

图3 棋盘

图4 立方体

表1 恢复图形区域强度处理方法对比

图5 原始视觉

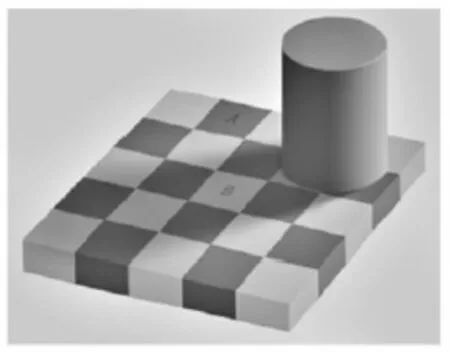
图6 NW方法

图7 TV-H1方法

图4 ～图6显示了棋盘上的视觉比较图片。类似于其他的例子，NW所提出的方法获得视觉上优选的输出，我们提出的方法中的恢复照明与NW相比反射率信息较少可以从立方体结论图像的比较中得出，见图4，可以注意到NW的亮度和结果我们是非常不同的。这主要是由于对于NW方法，强度值的事实左侧像素也用于解决泊松方程输出的右列和底行，由于边界条它亮度比图像的其他部分强。在该测试中，对于这两个示例，对于棋盘图像β=10，并且设置α=4，立方体图像α=10的。其约束条件是 Βr=[0 ， 255] 和 Βl=[0 ， 255]两个图像。

5 结语

在本文中，我们提出了一个新的反射率和照明基于高阶TV+H1正则化，这与infimal密切相关卷积一阶和二阶TV正规化。提出的模型可以很好地分离相对更平滑的分段线性分量。数值实验图片背景的非均匀性去除颜色阴影校正表明我们提出的模型提取HVS照明度更好，和细节保留的反射率，相比其他分解模型我们的模型更有效果。

［1］刘家朋，赵宇明，胡福乔.基于单尺度Retinex算法的非线性图像增强算法［J］.上海交通大学学报，2007，41（5）：685-688.LIU Jiapeng，ZHAO Yuming，HU Fuqiao.A Nonl inear Image Enhancement Algorithm Based on Single Scale Retinex［J］.Journal of Shanghai Jiaotong University，2007，41（5）：685-688.

［2］睢丹，焦振，杨杰.基于小波分析和Retinex算法的图像增强算法［J］.吉林大学学报：理学版，2016，54（3）：26-31.SUI Dan，JIAO Zhen，YANG Jie.Image Enhancement Algorithm Based on Wavelet Analysisand Retinex Algorithm［J］.Journal of Jilin University：Science Edition，2016，54（3）：26-31.

［3］刘钦堂.基于Retinex算法的彩色图像增强研究［D］.哈尔滨：哈尔滨工程大学，2012.LIU Qintang.Research on Color Image Enhancement Based on Retinex Algorithm［D］.Harbin：Harbin Engineering University，2012.

［4］陈炳权，刘宏立.基于全变分Retinex及梯度域的雾天图像增强算法［J］.通信学报，2014，35（6）：139-147.CHEN Bingquan，LIU Hongli.Algorithm for foggy image enhancement based on the total variational Retinex and gradient domain［J］.Journal of Communications，2014，35（6）：139-147.

［5］陈超.改进单尺度Retinex算法在图像增强中的应用［J］.计算机应用与软件，2013，30（4）：55-57.CHEN Chao.Application Of Improved Single Scale Retinex algorithm In Image Enhancement［J］.Computer Applications and Software，2013，30（4）：55-57.

［6］李学明.基于Retinex理论的图像增强算法［J］.计算机应用研究，2005，22（2）：235-237.LI Xueming.Image Enhancement AIgorithm Based on Retinex Theory［J］.Journal of Computer Applications，2005，22（2）：235-237.

［7］张素琦，刘巧红，李斌.混合高阶全变差正则化的运动模糊图像盲复原［J］.计算机应用研究，2016，33（8）：138-145.ZHANG Suqi，LIU Qiaohong，LI Bing.Hybrid high-order total variation regularization method for motion blur image blind restoration［J］.Journal of Computer Applications.2016，33（8）：138-145.

［8］郭从洲，秦志远.非凸高阶全变差正则化自然光学图像盲复原［J］.光学精密工程，2015，23（12）：3490-3499.GUO Congzhou，QIN Zhiyuan.Blind restoration of nature optical images based onnon—conVex high order total Variation regularization［J］.Optics and Precision Engineering.2015，23（12）：3490-3499.

［9］刘海波，汤群芳，杨杰.改进直方图均衡和Retinex算法在灰度图像增强中的应用［J］.量子电子学报，2014，31（5）：525-532.LIU Haibo.Improved histogram equalization and algorithm The Application of Gray Image Enhancement［J］.Chinese Journal of Quantum Electronics，2014，31（5）：525-532.

［10］苏亭.基于FPGA的Retinex算法实现［J］.信息通信，2013（10）：47-48.SU Ting.Realization of Retinex Algorithm Based on FPGA［J］.Information communication，2013（10）：47-48.

［11］Kimmel R，Elad M，Shaked D，et al.A Variational Framework for Retinex［J］.International Journal of Computer Vision，2003，52（1）：7-23.

［12］Rahman Z，Jobson D J，Woodell G A.Retinex processing for automatic image enhancement［J］.Journal of Electronic Imaging，2004，13（1）：100-110.

Realization of High Order Total VariationL1Decomposition Based on Retinex Algorithm

ZHANG Pengcheng
（Henan Broadcasting University，Zhengzhou 210098）

In this paper，the reflectivity and illumination decomposition model of the Retinex problem with high order total variation andL1decomposition are presented.Based on the observation that the illumination change is more smooth than the reflection，a convex variational model is proposed which can effectively decompose the image gradient field into a convex edge and relatively smooth illumination field through the first and second order total variation rules.The proposed model can be effectively solved by the original prima dual splitting numerical experiments on grayscale and color images show the strength of the proposed model for Image restoration，experiments show that the algorithm is feasible and effective.

Retinex algorithm，image decomposition，high-order total，variation，shadow correction

TP391

10.3969/j.issn.1672-9722.2017.10.029

Class Number TP391

2017年4月7日，

2017年5月26日

张鹏程，男，硕士，讲师，研究方向：软件工程、远程教育。