考虑组合分散化效应的股票质押定价分析

（上海交通大学安泰经济与管理学院, 上海 200030）

引言

股票质押业务目前在我国迅速发展，据Wind统计，2016年沪深两市共有53%的上市公司进行股票质押，股数达3067.64亿，涉及市值4.15万亿元，分别较2015年高出94.65%和46.13%。随股票质押业务迅猛发展，股票质押率定价的重要性开始凸显，它直接影响质权人的收益能否与风险合理匹配：若质押率过高，虽可提高对质押人的吸引力，从而助力业务规模扩张，但质权人融出的资金也往往会超出合理范围，致使其收益难以覆盖风险；若质押率过低，虽然风险很低，但这往往会削弱质权人的市场吸引力，导致业务规模被压缩。

关于股票质押率定价，在股票质押业务实践中，虽然业务框架已具备，但实践中的股票质押率定价方法严重落后于理论，而现有的理论定价方法也存在诸多缺陷。目前，理论界多是简单依据波动率风险来对单一股票标的进行定价，VaR(Value at Risk，在险值)方法被广泛用于股票质押率定价，其基本思想为：质权人参考一段时期的股票价格变化，在特定置信水平下估算质押期内股票的最大损失，进而转化为质押率以覆盖股票的价格风险。例如，王志诚等(2002)[17]基于沪深两市所有A股股票1995～2000年的数据，利用VaR风险测度方法来给出股票质押率；再如于辉等(2010)[20]、何娟等(2012)[10]，均是利用VaR方法确定质押率。但VaR只是度量在一定置信水平下的最大损失，它无法估计超出最大损失之外的超额损失，即它忽视了质押标的尾部损失，据其算得的折算率往往高估。因此，学界对基于VaR的质押率定价方法进行了改进：一是用CVaR(Conditional VaR，条件在限制)、ES(Expected Shortfall，预期不足)等测度代替VaR，以弥补VaR测度无法描述分位数之外损失的缺陷，如何娟等(2015)[11]在CVaR框架下，引入改进的均值方差优化技术，对质押率进行研究；二是VaR测度与GARCH模型结合，通过GARCH模型刻画的波动聚集来估计质押标的的尾部损失，如董珊珊(2012)[9]、李虹等(2016)[14]均提出利用GARCH模型测算股票质押率。

上述研究为本文提供了宝贵的理论借鉴，但精确度和实用性还明显不足，体现在以下两方面：

第一、现有股票质押率定价忽视了组合视角下的研究方法，即忽视了组合分散化效应对质押率定价的影响。在实际股票质押业务中，质权人更可能持有的是多只质押股票的组合(即一个质权人事实上会对应多位质押人，而质押人所质押的股票又不一样)。在传统股票质押率定价中(即质权人并非基于组合视角进行质押率定价)，质权人只是单独对每只股票进行质押率定价，而不考虑质押股票之间的相互关系。然而，根据Markowitz(1952)[8]或者说组合风险分散效应，质权人所持的质押股票组合的风险并不是单一股票风险的简单相加，此时，质权人整体质押业务风险不应是各质押股票所含风险的加权平均。因此，为实现质权人整体质押业务的风险--收益平衡，质权人必须基于组合视角进行质押率定价，即根据质押股票对质权人的风险贡献进行质押率定价。只有对组合风险进行分解，使之能够描述各质押股票对质权人总体风险的贡献大小，才能在此基础上得到合理的质押率。

第二、当以组合视角分析质押业务时，传统VaR方法并非理想的质押率定价方法。一方面，股票之间往往呈现非线性相关关系，基于线性相关系数的VaR方法难以准确地得到组合风险价值；另一方面，股票收益率多呈现尖峰厚尾、波动聚集等特征，组合收益率并不服从常见的多元正态分布。要准确计算组合VaR，必须准确地刻画各股票的边缘分布以及股票之间的相依结构。解决这一问题的方法之一就是Copula方法，Copula函数可将标的股票的边际分布与它们之间的相依结构分开研究，且股票的边缘分布选择不受限制，此时即可用GARCH模型刻画股票收益率的尖峰厚尾、波动聚集特征，其实用性和效率更高。但是多元Copula在刻画多资产相依结构及度量组合VaR等问题上存在缺陷：多元Copula函数假定金融资产间的相依结构必须用同一类Copula刻画，不允许组合中不同资产之间存在不同的相依结构，而在真实的金融市场中，金融资产间的相依结构并非完全一致(即组合中不同资产之间可能存在不同的相依结构)。为解决这一问题，Joe(1996)[7]提出了基于Pair Copula构造多维Copula模型的方法，Bedford and Cooke(2001,2002)[1][2]在Joe(1996)[7]基础上，进一步引入了称之为藤(Vine) Copula的相依结构。Vine Copula理论利用Pair Copula作为基础模块来建立多维Copula模型，它允许不同随机变量之间存在不同的Copula相依结构，较多元Copula，Vine Copula在刻画多维随机变量间的相依结构上具有更强的灵活性和实用性。目前，Vine Copula已广泛应用于多元数据建模，例如Heinen and Valdesogo(2009)[6]运用C-vine建立了多只股票收益率之间的动态相依结构模型；李磊等(2013)[15]基于C-vine Copula估计了相应投资组合的CVaR；居姗等(2013)[13]基于D-vine Copula给出了多资产投资组合的VaR估计方法。但值得强调的是，Bedford and Cooke(2001, 2002)[1][2]提出Regular Vine Copula(简记为R-vine Copula)，较C-vine和D-vine(C-vine和D-vine仅是R-vine的特殊结构，C-vine呈星型结构，D-vine呈平行结构)更适于有效预测组合VaR，如吴海龙等(2013)[18]、马锋等(2015)[16]的实证研究均表明R-vine Copula对投资组合VaR的预测效果最好。

基于上述认识，本文开展以下研究工作：首先将单一股票质押问题扩展至组合质押视角，利用AR(1)-GARCH(1, 1)模型分析各股票收益率的边缘分布，以刻画收益率分布的尖峰厚尾、波动聚集等典型分布特性；其次，在刻画边缘分布的基础上，采用R-vine Copula模型对多元数据进行建模，得到任意n只股票收益率的联合分布和相依结构；最后结合Monte Carlo模拟方法，利用Copula-GARCH的组合VaR分解技术得到各质押股票对应的成分VaR以反映其风险贡献，进一步得到其相应的质押率，并与基于传统VaR情形的质押率定价进行对比验证。

基于R-vine Copula-GARCH的质押率定价模型

本文把单一股票质押问题扩展至组合质押视角，以考虑质权人组合分散化效应对质押率定价的影响，目的在于提高质押业务整体风险--收益平衡性。传统上，即使质权人持有多只质押股票，质权人也只是单独对每只股票进行质押率定价，而不考虑质押标的之间的相依结构；而在基于质权人视角的质押问题中，质权人会将其所有质押股票看作一个投资组合来考虑风险，然后根据质押股票的风险贡献进行质押率定价。

质押率反映的是质押标的的预期损失被覆盖后，质权人融出资金占质押标的期初价值之比。基于传统VaR方法的质押率β可表示如下：

其中，VaR表示一定显著性水平下的VaR值；显著性水平通常等于0.01，即质权人据此设定质押率后，面临损失的概率为1%。

在传统定价方法中，质权人一般根据式(1)计算每只股票的VaR，进一步得到每只股票的质押率。它的问题在于各股票的VaR并不等价于其风险贡献，这是因为质权人持有的是质押股票的组合，由于组合分散化效应，组合内各股票的加权VaR之和一般不等价于组合VaR，即各股票的加权风险之和并不等价于质权人的组合风险。事实上，根据成分VaR的定义(若某只股票被剔除出组合后，组合VaR的近似变化量即使成分VaR)可知，成分VaR反映了组合内各股票对组合的风险贡献大小，各股票的成分VaR之和等于组合VaR。对应地，此时质押股票i的质押率βi为

本文利用R-vine Copula-GARCH模型刻画多股票的联合分布，在此基础上计算组合VaR，并基于VaR分解技术得到各质押股票的成分VaR，进一步基于式(2)得到各股票的质押率。具体实现步骤如下：①基于AR(1)-GARCH(1, 1)估计各质押标的收益率的边缘分布；②通过R-vine Copula函数估计多个质押标的间的多元相依结构；③利用Monte Carlo模拟法，计算基于R-vine Copula-GARCH的组合VaR；④根据组合VaR分解技术，得到各质押标的成分VaR，并据此得到其相应的质押率。

一、质押股票收益率分布模型

实证研究表明，股票收益率序列具有自相关性和异方差性。因此，本文利用AR-GARCH模型分析各股票收益率的边缘分布，以刻画其尖峰厚尾、波动聚集等典型分布特性。Bollerslev(1986)[3]研究表明AR(1)-GARCH(1,1)即可描述股票收益率的波动情况，模型如下：对t时刻的对数收益率序列进行一阶自回归AR(1)拟合，再对拟合后的残差序列进行GARCH(1, 1)建模。考虑n只股票的组合，记股票i在t时刻的对数收益率为Ri,t，其中i=1, 2, …,n。基于AR(1)-GARCH(1, 1)的收益率建模方法如下

其中，Ri,t为对数收益率，μi为收益率均值，σi,t为收益率波动率，Zi,t为新息项，满足E(Zi,t)=0、VAR(Zi,t)=1。μi，αi，ai,0，ai，bi为模型待估参数。

二、通过Copula函数估计n只股票间的多元相关结构

在实际中，股票间往往存在复杂相关结构(如尾部相关、非线性相关等)，基于线性相关关系的传统VaR分析容易导致错误结果。而Copula函数不仅可用于度量股票之间的非线性相关关系，而且可将其边缘分布与它们之间的相依结构分开研究，边缘分布选择也不受限制，它已成为构建多维随机变量联合分布和分析随机变量间相依结构的重要工具。因此，本文选择Copula函数描述多只股票间的相依结构。Copula函数定义如下：F为n维随机变量X1,X2, …,Xn的联合分布函数，其中Xi～Fi(i=1, 2,…,n)，即Fi为Xi的边际分布函数，则F为边际分布F1,F2,…,Fn的Copula函数C(.)，即

根据式(4)，多维联合密度函数可以划分成两部分：边缘密度函数和变量间的相依结构—Copula密度函数。不同的Copula描述了不同的相关模式，如Gumbel Copula函数对分布的上尾相关更加敏感(下尾相关系数为0)；Clayton Copula函数对分布的下尾相关更加敏感(上尾相关系数为0)；而t-Copula函数、Gaussian Copula函数、Frank Copula函数可用于描述对称相关模式，其中Gaussian Copula函数和Frank Copula函数的上下尾相关系数均为0。然而，传统Copula在描述多元相依结构时，只能选择一种类型(例如，多元Clayton Copula则意味着资产之间均下尾相关)，它不能充分反映资产组合内两两资产间的相关性，从而导致对多维相依结构的估计存在偏差。而基于R-vine Copula理论构建的多维Copula模型，允许不同随机变量之间存在不同的相依结构，即不同随机变量之间可以存在不同形式的Copula相依结构，所以它在刻画多维随机变量间的相依结构上具有明显优势。吴海龙等(2013)[18]，马锋等(2015)[16]的实证研究均表明R-Vine Copula对投资组合VaR的预测效果最好。因此，本文采用R-vine Copula描述质押股票间的相依结构，R-vine Copula的密度函数如下

关于R-vine Copula的具体介绍及解读，可参见Dissmann et al.(2013)[5]、Brechmann and Schepsmeier(2013)[4]。

三、基于R-vine Copula模型的组合VaR分析

基于步骤(一)和步骤(二)，R-vine Copula-GARCH构建了n只股票间的联合概率分布函数。在得到任意n只股票的联合分布和相依结构的基础上，结合Monte Carlo模拟法，即可得到质权人资产组合的在险值VaR。

投资组合的VaR指的是：给定某个置信水平α∈(0,1)，VaR是使该组合损失L超过l(L≥l)的概率不大于1-α的最小l，即

其中，Fp表示该投资组合收益率的概率分布函数。考虑包含n只股票的组合P，记第i个标的资产所占的权重为wi，那么质权人资产组合P收益率Rp,t为

基于R-vine Copula-GARCH模型的VaR并不存在解析解，此时，需采用Monte Carlo模拟法计算组合VaR。对步骤(二)确定的R-vine Copula进行抽样，以模拟资产组合的收益率。需要注意的是，本文是对经过AR(1)-GARCH(1,1)模型滤波之后的标准化残差收益序列{Zi,t}进行建模，因而R-vine Copula抽样得到的是Zi,t的仿真序列。在模拟过程中，将t-1日的波动率σi,t-1代入GARCH模型中即可得到t日的波动率估计值，再将模拟得到的Zi,t和带入AR模型中，便能计算出该股票t日收益率Ri,t的估计值则基于式(7)即可得到组合t日收益率的估计值，重复抽样N次，即可计算出该质押标的组合当天的VaR值。另外，实践中，通常根据金融资产1天的VaR1来估计金融资产T天的VaRT，方法如下：

四、组合VaR分解及质押率确定

一般来说，单纯的组合VaR值对质权人了解风险的主要来源不能提供有意义的参考价值，质权人也无法据此得到质押率定价。因此，只有对组合VaR进行分解，使之能够描述各股票对组合总体风险的贡献大小，进而才能在此基础上得到质押率。

设ri*表示组合在置信水平为α的条件下取最小值W*时资产i的收益率，此时

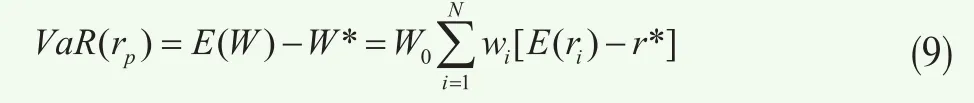
即组合VaR是资产权重{wi}，i∈p的齐次线性函数，由欧拉分配定理可知

其中，M-VaRi为资产i的边际VaR，此时可得到，

因此，只要知道组合中各股票的边际VaR，即可根据式(11)可得到其成分VaR。估计边际VaR的方法已经相对成熟，参见胡海鹏等(2003)[12]、吴绪权等(2006)[19]。本文不赘述。在估计得到边际VaR之后即可得到各股票的质押率，即

数值算例

一、数据描述

假设质权人持有6只质押标的，它们分别是“浦发银行(600000)”、“恒瑞医药(600276)”、“深圳能源(000027)”、“东方雨虹(002271)”、“长海股份(300196)”和“朗科科技(300042)”，编号依次为1至6。事实上，在实际的股票质押业务中，虽然不同的质权人持有的股票组合是不同的，但是对任一质权人而言，质权人持有的质押股票组合是确定的，此时，即可进一步确定组合中各股票的波动率、各股票在组合中所占的权重以及质押股票之间的相依结构。一旦质权人根据实际质押股票组合确定了上述关键参数，即可使用本文提出的模型，根据质押股票的风险贡献确定质押率的合理定价，本文模型具有通用性。

质权人基于组合质押视角，对这六只股票的收益率进行R-vine Copula-GARCH建模，并在得到每只股票风险贡献的基础上进一步确定其质押率。本文选取的样本区间为2016年1月4日～2016年12月31日，质权人在2017年1月4日进行质押率定价。假设质权人持有的这6只股票的质押数量均为1亿股，根据2016年12月31日的收盘价数据，这6只质押标的在质权人所持组合中的权重分为10%、29%、4%、14%、24%和20%(注：在实际质押业务中，质权人可根据其所持的实际质押股票数量得到质押标的的权重)。上述6只股票收益率(收益率指的是日对数收益率)序列的统计特征见表1。

表1 样本区间内质押标的收益率的统计特征

根据表1可知，6只质押标的收益率的偏度系数均小于0，说明质押标的收益率序列存在一定的左偏；6只质押标的收益率的峰度系数均大于3，说明质押标的收益率均呈现尖峰厚尾特征；另外，根据J-B统计量检验可知，收益率序列服从正态分布的假设被拒绝；而Engle’s ARCH Test统计量表明，在1%显著性水平上，收益率序列具有明显的ARCH效应。为消除单只质押股票收益率序列的自相关性和异方差性，本文采用AR-GARCH模型对质押股票收益率进行建模，以刻画其尖峰厚尾、波动聚集的特征。

二、股票收益率的边际分布估计

利用AR(1)-GARCH(1, 1)模型对这6只股票的收益率序列进行拟合，参数估计结果见表2。

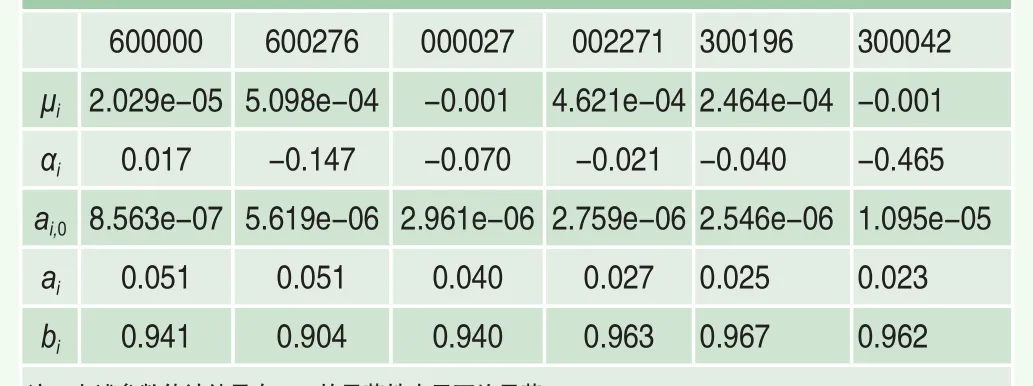
表2 AR(1)-GARCH(1,1)模型的参数估计结果

三、基于R-vine Copula的联合分布估计

本节估计这6只股票的R-vine Copula结构，R-vine Copula模型的输入变量是“经过AR-GARCH模型滤波之后的标准化残差收益序列{Zi,t}”，利用Python的pyvine0.4.2模块直接得到R-vine Copula模型的参数估计结果，见表3。

表3中，节点i表示股票i的概率密度分布，例如节点1表示股票1(即浦发银行)的概率密度分布，节点23表示股票2和股票3(即恒瑞医药和深圳能源)的联合概率密度，节点46|5表示的则是条件概率密度。根据表3可知，质押股票之间存在复杂的相依结构(例如，节点1和节点2之间的相依结构是Student Copula，而节点5和节点6之间的相依结构是Clayton Copula)，单纯利用多元Copula很难刻画资产之间的相依结构，因为多元Copula假定所有资产之间仅存在一种Copula相依结构。这意味着R-vine Copula模型在对多维资产收益率数据进行建模时更加具有灵活性，在对两两资产之间的Copula的选择上更为准确。

四、组合VaR分解及其相应的质押率

表3 R-vine Copula模型的参数估计结果

在得到R-vine Copula模型之后，利用Python模块pyvine得到基于R-vine Copula抽样的仿真序列。值得注意的是，R-vine Copula抽样得到的是Zi,t的仿真序列，即R-vine Copula抽样得到的是Zi,t的仿真序列，即R-vine Copula抽样得到的是经AR-GARCH模型滤波之后的标准化残差收益序列{Zi,t}。股票i在t日收益率Ri,t的估计值的计算方法如下：

将t-1日的波动率σi,t-1代入GARCH模型中计算质押标的在t日的波动率的估计量σi,t-1，再将模拟得到的Zi,t和带入AR模型中，便能得到该股票t日收益率Ri,t的估计值结合其权重向量，利用式(7)即可得到质权人所持组合在t的收益率的估计值重复上述步骤N次，便可得到基于R-vine Copula-GARCH模型的组合VaR值。在此基础上，利用组合VaR分解技术，并结合式(13)即可得到各股票的质押率，见表4。为便于阐述模型效果，本文还列示了独立VaR情形和传统组合VaR分解情形下的质押率定价结果。

通过对比表4可得如下结论：

第一、质权人是否基于组合视角将对股票质押率定价产生重要影响。单纯对比独立VaR情形和传统组合VaR分解情形，二者的区别在于是否考虑组合的分散化效应，组合的风险并不是单一股票风险的简单相加，即质权人的整体质押业务风险不应是各股票所含风险的加权平均。传统组合VaR分解考虑了组合分散化效应，它对应的质押率要高于不考虑分散化效应的独立VaR情形，即质权人不基于组合视角将低估质押率。

第二、基于R-vine Copula-GARCH VaR分解情形的质押率低于传统组合VaR分解情形，即忽视收益率尖峰厚尾特征和收益率之间的复杂相关结构，将高估质押率。传统组合VaR模型假定股票收益率之间服从多元正态分布，即质押标的收益率之间均是线性相关，且不存在尖峰厚尾特征。但正如前文实证结果所示，股票收益率均存在尖峰厚尾、波动聚集现象(见表3)，而且股票之间存在复杂相依结构(见表4)，在考虑这些因素之后，质押率应有所降低。

对比这三种定价情形，质权人不基于组合视角定价将低估质押率；进一步来比较前两种定价方法，同是基于组合视角，当充分质押标的收益率尖峰厚尾和复杂相关时，质押率变会稍低。这就意味着本文结合R-vine Copula模型和AR(1)-GARCH(1, 1)模型给出的质押率定价方法，既有利于提高质权人风险防范度，又可避免质权人过度防范风险，在三种方法中，最能实现风险-收益的平衡。

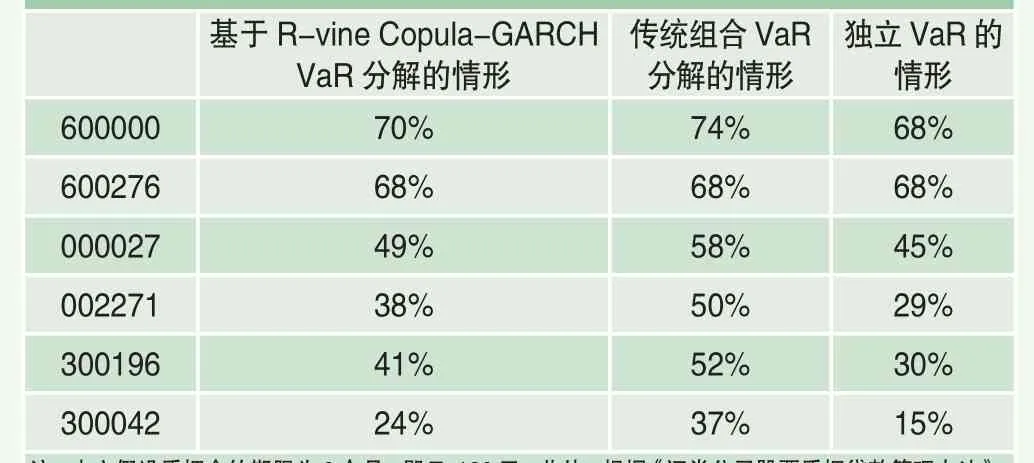
表4 不同模型下的质押率定价对比

本文不仅具有理论意义，而且也具有现实指导意义。目前，实践中的股票质押率定价方法严重落后于理论，证券公司一般根据所谓的“五四三”标准来设定不同个股的质押率，即令波动率最小的主板股票质押率为50%，中小板为40%，而波动率最大的创业板股票质押率为30%。但是这类定价方法精确度明显不够，进而导致质权人风险--收益难以平衡。而本文提出的考虑组合分散化效应的质押率定价方法，为国内证券公司在质押率定价、风险控制等微观层面的设计提供了明确的指引。

结论

为促进股票质押业务健康发展，合理匹配质权人的收益与风险，优化质押率定价显得颇为重要。而理论界对质押率做定价基本都针对单一股票标的，这事实上忽略了质权人的组合分散化效应对质押率定价的影响。此外，实践中广泛使用的VaR定价方法，也忽视了质押标的收益率尖峰厚尾、波动聚集等特征对质押率定价的影响。鉴于此，本文将研究视角由单一股票质押率定价扩展至考虑分散化效应的组合质押问题，首先利用AR(1)-GARCH(1, 1)估计各质押标的收益率的边缘分布函数，然后通过R-vine Copula 函数估计多个质押标的间的多元相关结构，最后结合Monte Carlo模拟和组合VaR分解技术得到质押率定价模型，并通过数值算例验证上述定价方法的优势。

概括而言，本文贡献主要包括：第一，把单一股票质押问题扩展至考虑分散化效应的组合质押问题，更切实际；第二，充分考虑了质押标的收益率的尖峰厚尾特征及其复杂相关结构，结合AR-GARCH模型及R-vine Copula模型，根据质押标的的风险贡献进行质押率定价，有助于提高实际质押业务的整体风险——收益平衡性。