切换拓扑下无人机集群系统时变编队控制

周绍磊， 祁亚辉， 张雷， 闫实， 康宇航

海军航空工程学院 控制工程系， 烟台 264001

切换拓扑下无人机集群系统时变编队控制

周绍磊*， 祁亚辉， 张雷， 闫实， 康宇航

海军航空工程学院 控制工程系， 烟台 264001

针对多无人机(UAV)间通信拓扑可能发生变化的情况，研究了具有二阶积分特性的无人机集群系统的轨迹跟踪与时变编队控制问题。基于一致性方法设计了编队控制器，将编队控制问题转换成闭环系统的稳定性问题，引入了切换拓扑平均驻留时间的概念，并在此基础上利用线性矩阵不等式(LMI)方法，给出了控制器设计步骤。通过构造分段连续Lyapunov函数，证明了切换拓扑下无人机集群系统能够实现对指定轨迹的跟踪并且实现时变编队飞行。以三维空间运动的无人机集群系统为例进行了仿真验证，结果表明本文所提方法能够解决切换拓扑下无人机集群系统的轨迹跟踪与时变编队问题。

无人机； 集群系统； 切换拓扑； 一致性； 编队控制； 轨迹跟踪

近年来，集群系统的编队控制因其在军事和民用领域具有广泛的应用前景而吸引了众多学者的关注，并取得了大量研究成果[1-2]。传统的控制方法主要有基于行为的控制方法[3]、leader-follower方法[4-5]和基于虚拟结构的方法[6]。

伴随着一致性理论的发展[7-10]，基于一致性理论的编队控制也取得了丰硕的研究成果[11-17]。其中文献[11]系统地介绍了一致性方法在二阶积分系统轨迹跟踪和编队控制中的应用，并且表明基于行为的、leader-follower和基于虚拟结构的编队控制方法都可以认为是基于一致性方法的特例。随后文献[12]中将理论方法应用于多机器人系统。文献[13]给出了无向图下，二阶集群系统实现编队控制的充分条件。文献[14]研究了离散多智能体系统的轨迹跟踪与编队形成问题，给出了基于一致性控制器的设计方法。文献[15]研究了切换拓扑下具有一阶积分特性的多智能体系统的轨迹跟踪与编队控制问题。文献[16-17]分别研究了无人机在无向切换通信拓扑和有向通信拓扑下的时变编队问题，并使用小型旋翼无人机进行了实验验证。文献[18]采用一致性方法，用完全分布式控制器解决了有向切换拓扑通信条件下的无人机编队问题。虽然以上文献从不同方面给出了编队形成的一致性控制器，但大都是针对固定通信拓扑[11-14, 17]。根据文献[10，19]可知，即使对于每一个固定通信拓扑系统渐进稳定，切换拓扑系统也未必稳定。文献[15]研究了切换拓扑系统的编队问题，但是其控制器要求已知所有拓扑图的并集，并且其控制方法只适用于一阶积分模型。文献[16]虽然研究了切换拓扑下的编队问题，但是针对无向通信网络，其研究结果表明，无向图下编队形成与拓扑切换与否无关。对于有向切换拓扑图下基于一致性的编队问题，文献[16]的结论并不适用。文献[18]虽然针对有向切换通信拓扑，但是其假设所有可能的通信拓扑图都是强连通和平衡的，这对通信拓扑要求过于严苛，不具有普遍性。对于一般有向切换拓扑通信条件下，保证集群系统编队形成的一致性控制器设计问题的相关研究还比较少。

本文在一致性理论和切换系统理论研究成果基础上，重点解决有向切换通信拓扑条件下的具有二阶积分动态特性的无人机轨迹跟踪和时变编队问题。相比已有的研究成果，本文对集群系统间通信拓扑的要求更为普通，不但针对有向通信网络，而且适用于随时间切换通信拓扑的系统。

1 预备知识

1.1 符号约定

符号RN×N和CN×N分别表示N×N维的实矩阵和复矩阵。对于任意μ∈C，其实部表示为Re(μ)。IN是N×N维的单位矩阵。对于矩阵A∈RN×N，λ(A)表示其特征值；max{λ(A)}和min{λ(A)}分别表示矩阵A的最大和最小特征值。A>B和A≥B分别表示A-B是正定和半正定的。A⊗B表示矩阵A和B的Kronecker积。

1.2 图论

1.3 相关引理

引理1[7]图G的Laplacian矩阵L至少有一个零特征值，其他非零特征值均具有正实部；如果G包含有向生成树，则零是L的单特征值，1N是其对应的右特征向量。

引理2[20]如果矩阵W∈RN×N所有特征根均具有正的实部，那么存在一个正定矩阵Q>0使得WTQ+QW>0。

2 问题描述及编队控制器设计

2.1 问题描述

考虑由N个无人机组成的集群系统，多无人机之间通信拓扑用有向图G描述。无人机i∈{1,2,…,N}认为是G的节点vi。

主要研究无人机集群系统的轨迹跟踪与编队形成，不考虑无人机内环动态，把单个无人机视为质点，其动态采用二阶积分模型[16-17,21]：

(1)

式中：xi(t)和vi(t)分别为第i个无人机的位置和速度；ui(t)为其对应的控制输入。假定无人机三维运动相互解耦，为便于描述，以一维运动进行分析。

(2)

h(t)=[h1(t)h2(t) …hN(t)]T

定义1[17]时变编队可以用一组函数hi(t)(i=1,2,…,N)表示，对于给定的队形h(t)和某轨迹c(t)，如果无人机集群系统(2)在任意的初始给定情况下满足：

(3)

则称无人机实现了时变编队h(t)，c(t)称为编队中心轨迹。

基于一致性方法，控制器设计为[11,13]

(4)

式中：i=1,2,…,N；K1,K2∈R1×2为待设计的控制参数。为了书写方便，式(4)中各时变物理量略去了时间描述(t)，下同。

将式(4)代入式(2)，令

ξ(t)=[ξ1(t)ξ2(t) …ξN(t)]T

得到的闭环系统方程为

[IN⊗(BK1)-Lσ(t)⊗(BK2)]h+

(IN⊗B)hv-[1N⊗(BK1)]c+

(5)

本文研究的主要内容就是在切换通信拓扑条件下，如何设计控制器使无人机集群系统实现对轨迹c跟踪和保持时变编队h。

2.2 问题分析和控制器设计

根据定义1，令θi=ξi-hi-c，由式(5)及引理1可以得到

(6)

所以系统(6)可以进一步化为

(7)

显然如果系统(7)收敛于0，那么系统(2)就实现了轨迹跟踪和时变编队，所以下面重点就是分析如何使系统(7)收敛于0，因为Gσ(t)在任意时刻都是有向图，不能进行简单的解耦分析[16]，首先参考文献[9]中一致性控制器设计方法，令K=-K1=K2，则系统(7)转变为

(8)

引理3对于矩阵IN+Lσ(t)，存在变换的正定矩阵Qσ(t)，使得式(9)成立：

(9)

式中：0<α<1。

证明根据引理1和引理2，存在正定矩阵Qσ(t)>0及0<α<1使得

Lσ(t)-αIN)>0

整理得到式(9)。

定义2对于随时间变化的通信拓扑图Gσ(t)，其在时间区间[0,t)上的平均驻留时间τa定义为

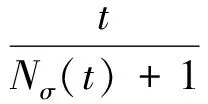
(10)

式中：Nσ(t)为Gσ(t)在时间区间[0,t)上的切换次数，也即σ(t)的变化次数。

注1关于平均驻留时间的概念，文献[10,22-24]中也给出了其定义：在时间区间[t0,t)上，如果存在N0≥0和τa>0使得

(11)

成立，则τa称为平均驻留时间。笔者认为此定义是不准确的，这些文献都参考了文献[19]。在文献[19]中，平均驻留时间并不是以定义的形式给出的，只是用平均驻留时间的概念定义一个集合，该集合满足式(11)。直观地讲，当Nσ(t0,t)为1，τa为接近0的正小量时，式(11)右侧为无穷大，不等式成立，但是平均驻留时间定义为正的无穷小是不合理的。此外，根据式(10)，当N0=0时，可以得到式(11)。

根据以上分析，结合切换系统平均驻留时间的概念，控制器设计算法为

算法1

1) 如果切换拓扑系统平均驻留时间为τa，取

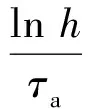
(12)

ATP+PA-2αPBBTP+βP≤0

(13)

2) 取K=BTP，K1=-K，K2=K。

定理1如果假设1成立，则由算法1设计得到的控制器，能够使无人机集群系统(2)在切换拓扑条件下实现轨迹跟踪和时变编队。

证明考虑分段连续的Lyapunov函数

V=θT(Qσ(t)⊗P)θ

(14)

式中：Qσ(t)和P分别满足式(9)和式(13)。

当t∈[tk,tk+1)时，V是连续的，对其求导并将式(8)代入，同时令K=BTP可得

θT{[(IN+Lσ(t))TQσ(t)+

Qσ(t)(IN+Lσ(t))]⊗PBBTP}θ

由式(9)可得

(15)

又因为式(13)可得

(16)

根据式(14)和式(16)可知

V(t)≤e-β(t-tk)V(tk)

(17)

在拓扑切换时刻tk，存在关系：

(18)

V(t)≤e-β thkV(0)

(19)

(20)

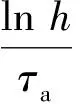
此外，根据式(15)可得，对于固定通信拓扑，无人机集群系统要实现编队飞行，只需在控制器设计时令P满足：

ATP+PA-2αPBBTP≤0

(21)

即可。显然式(21)成立是式(13)成立的必要条件，也即本文控制器设计方法必然适用于固定通信拓扑。

另根据式(12)、式(20)可以看出，β取值越大，θ(t)收敛速度越快，也即编队能够更快地形成；从能量角度分析，β参数的引入是为了使能量减小的速度抵消拓扑切换可能带来的能量增加。

注2控制器(4)包含自反馈，根据推导过程可以看出，假设1并不是无人机集群系统实现轨迹跟踪和时变编队的必要条件，甚至在无人机间不存在通信关系，即Lσ(t)≡0的情况下，轨迹跟踪和时变编队依然能够实现。但是根据文献[11-12]可知，通信拓扑包含有向生成树能够提高集群系统编队形成的暂态性能，增强系统鲁棒性。

特别地，考虑无人机集群系统中并非所有无人机都能实时获取自身位置，只有一处于根节点位置的无人机能够得到自身实时位置，而其他无人机仅能获取与自身有拓扑联系的无人机的相对信息。此时将有部分无人机不能形成位置自反馈而必须依靠相对位置信息形成编队。控制器将变为

(22)

式中：当无人机i处于通信拓扑根节点时，gi=1，否则gi=0。

相应地，控制输入变化后的系统闭环方程式(8)变为

(23)

式中：Gσ(t)=diag(g1,g2,…,gn)为对角阵。

由文献[9]可知，如果Lσ(t)包含有向生成树且Gσ(t)在至少一个根节点位置取值大于0，则有Re(λ(Gσ(t)+Lσ(t)))>0，所以存在正定矩阵Qσ(t)和

0<α

(24)

使得

(25)

证明略。

不难发现，对于控制输入(22)，定理1结论依然成立，只是算法1中α和h取值发生了变化。相比控制输入(4)，控制输入(22)对无人机集群系统控制力减弱，但是利用本文控制方法，仍能实现切换通信拓扑条件下无人机集群系统时变编队控制。

3 仿真验证

考虑一个包含4架无人机的集群系统，在三维空间进行轨迹跟踪和时变编队飞行，系统状态和系统矩阵为

式中：i=1,2,3,4；xi1、xi2、xi3、xi4、xi5和xi6分别表示第i架无人机的东向位置、速度，北向位置、速度，高度及天向速度。

无人机初始状态为

编队中心轨迹设定为

时变编队设定为

i=1,2,3,4

集群系统间通信拓扑图和切换信号分别如图1 和图2所示。假定只有1号无人机(均位于根节点)能够获取自身位置，即有Gσ(t)=diag(1,0,0,0)，根据式(24)，取α=0.24，进一步根据式(25)分别求得相应的Q矩阵，得到h=5.87。根据图2中10 s内通信拓扑切换情况，可得切换系统平均驻留时间τa=1.25，根据式(12)取β=1.5。

根据2.2节分析，通过求解式(21)得到的控制器能够使固定通信拓扑下多无人机系统实现编队飞行，为便于比较，将此方法称为一般控制方法；将由算法1求解得到的方法称为本文控制方法。通过求解,最终得到一般控制方法控制参数：

图1 通信拓扑
Fig.1 Communication topologies

图2 通信拓扑切换信号
Fig.2 Switching signal of communication topologies

和本文控制方法控制参数

K2=-K1=

利用Matlab平台进行控制系统仿真，图3(a)和图3(b)分别为一般控制方法和本文控制方法下无人机高度变化轨迹。可以看出，两种方法下各无人机均能达到轨迹和编队指定高度，但是显然，本文控制方法能够使无人机集群系统更快地到达指定位置。

图4(a)和图4(b)分别为两种控制方法下无人机在东向位置上对编队中心轨迹和时变编队的跟踪误差，北向具有相似的变化规律，这里略去。从图4可以看出，虽然两种方法均能使误差最终收敛于0，但是本文控制方法能够使收敛速度更快。图5(a)和图5(b)分别为两种控制方法下无人机东向输入情况，可以看出本文控制方法在编队未形成时控制作用更大一些，这也使得编队更快形成。

虽然本文控制方法相较于一般控制方法使编队更快形成，但是可以看出，一般控制方法也能使无人机集群系统在切换通信拓扑条件下跟踪指定轨迹并形成编队。从2.2节推导过程可以看出，式(13)只是切换拓扑下式(7)收敛的充分条件而不是必要条件，由算法1得到的本文控制方法具有一定保守性。此外，式(13)成立是式(21)成立的充分不必要条件，也就是说本文控制方法必然能够使无人机集群系统在固定通信拓扑条件下形成编队，但是一般控制方法无法保证切换通信拓扑条件下编队一定能够形成。

图3 不同控制方法下无人机高度变化轨迹
Fig.3 Height variable trajectories of unmanned aerial vehicles (UAVs) with different controllers

图4 不同控制方法下无人机东向跟踪误差
Fig.4 Eastern tracking errors of UAVs with different controllers

还有一点需要指出，本文控制方法并未考虑输入饱和的情况，当无人机初始轨迹或队形偏差较大时，直接用本文控制方法得到输入量可能超过实际无人机的允许范围，必须进行限幅。并没有给出输入饱和情况下的收敛性证明,但是通过在仿真中对输入加入限幅发现，编队的形成趋势并未受到明显影响，图6(a)和图6(b)为在输入饱和约束条件下，用本文控制方法，加入±5的限幅后，无人机集群系统东向跟踪误差和输入。图6(a)和图4(b)比较可以看出，加入输入饱和约束后，跟踪误差在初始阶段收敛速度略缓，但是最终收敛时刻并未明显变长，甚至发散。所以本文控制方法对切换通信拓扑条件下无人机集群系统编队控制具有一定的参考价值，至少在轨迹或编队偏差不大时或者编队保持过程中具有一定实用性和优越性。

图5 不同控制方法下无人机东向输入
Fig.5 Eastern inputs of UAVs with different controllers

图6 输入饱和约束条件下无人机东向跟踪误差和输入
Fig.6 Eastern tracking errors and inputs of UAVs with saturation constraints

4 结 论

利用一致性问题研究中的相关思想和方法，给出了控制器及控制参数设计方法，解决了能描述为二阶积分模型的无人机集群系统轨迹跟踪与时变编队问题。

1) 控制器参数可以通过求解线性矩阵不等式得到，相比一般固定拓扑结构的一致性问题求解，线性矩阵不等式需要增加一个和通信拓扑平均驻留时间约束有关的附加项。

2) 通过选取合适的附加项参数，能够使编队形成的速度加快，以此抵消拓扑切换带来的影响，最终使无人机集群系统实现给定轨迹跟踪并且形成时变编队。

[1] NIGAM N, BIENIAWSKI S, KROO I, et al. Control of multiple UAVs for persistent surveillance: Algorithm and flight test results[J]. IEEE Transactions on Control Systems Technology, 2012, 20(5): 1236-1251.

[2] HAN J, XU Y, DI L, et al. Low-cost multi-UAV technologies for contour mapping of nuclear radiation field[J]. Journal of Intelligent & Robotic Systems, 2013, 70(14): 401-410.

[3] BALCH T, ARKIN R C. Behavior-based formation control for multirobot teams[J]. IEEE Transactions on Robotics and Automation, 1998, 14(6): 926-939.

[4] HE F, WANG Y, YAO Y, et al. Distributed formation control of mobile autonomous agents using relative position measurements[J]. IET Control Theory & Applications, 2013, 7(11): 1540-1552.

[5] DESAI J P, OSTROWSKI J P, KUMAR V. Modeling and control of formations of nonholonomic mobile robots[J]. IEEE Transactions on Robotics and Automation, 2001, 17(6): 905-908.

[6] LEWIS M A, TAN K. High precision formation control of mobile robots using virtual structures[J]. Autonomous Robots, 1997, 4(4): 387-403.

[7] REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.

[8] LI Z, DUAN Z, CHEN G, et al. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2010, 57(1): 213-224.

[9] LIU W, LIU A, ZHOU S. DistributedH∞control of multi-agent systems with directed networks[J]. Chinese Physics B, 2015, 24(9): 73-79.

[10] SABOORI I, KHORASANI K.H∞consensus achievement of multi-agent systems with directed and switching topology networks[J]. IEEE Transactions on Automatic Control, 2014, 59(11): 3104-3109.

[11] REN W. Consensus strategies for cooperative control of vehicle formations[J]. IET Control Theory & Applications, 2007, 1(2): 505-512.

[12] REN W, SORENSEN N. Distributed coordination architecture for multi-robot formation control[J]. Robotics and Autonomous Systems, 2008, 56(4): 324-333.

[13] XIE G, WANG L. Moving formation convergence of a group of mobile robots via decentralised information feedback[J]. International Journal of Systems Science, 2009, 40(10): 1019-1027.

[14] WANG J, NIAN X, WANG H. Consensus and formation control of discrete-time multi-agent systems[J]. Journal of Central South University of Technology, 2011, 18(4): 1161-1168.

[15] NIAN X, SU S, PAN H. Consensus tracking protocol and formation control of multi-agent systems with switch-ing topology[J]. Journal of Central South University of Technology, 2011, 18(4): 1178-1183.

[16] ZHOU Y, DONG X, LU G, et al. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies[J]. Control Engineering Practice, 2014, 46: 1203-1209.

[17] DONG X, YU B, SHI Z, et al. Time-varying formation control for unmanned aerial vehicles: Theories and applications[J]. IEEE Transactions on Control Systems Technology, 2015, 23(1): 340-348.

[18] 刘伟， 周绍磊， 祁亚辉， 等. 有向切换通信拓扑下多无人机分布式编队控制[J]. 控制理论与应用, 2015, 32(10): 1422-1427.

LIU W, ZHOU S L, QI Y H, et al. Distributed formation control for multiple unmanned aerial vehicles with directed switching communication topologies[J]. Control Theory & Applications, 2015, 32(10):1422-1427 (in Chinese).

[19] HESPANHA J P, MORSE A S. Stability of switched systems with average dwell-time[C]//Proceedings of the 38th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 1999: 2655-2660.

[20] CBEN C T. Linear system theory and design[M]. New York: Holt, Rinehart and Winston, Inc., 1970: 132-134.

[21] SEO J, KIM Y, KIM S, et al. Consensus-based reconfigurable controller design for unmanned aerial vehicle formation flight[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2012, 226(7): 817-829.

[22] WU L, LAM J. WeightedH∞filtering of switched systems with time-varying delay: Average dwell time approach[J]. Circuits, Systems and Signal Processing, 2009, 28(6): 1017-1036.

[23] DANIEL L. Switching in systems and control[M]. Boston: Birkhauser, 2003: 58-59.

[24] 方志明. 切换系统稳定性分析与优化控制若干问题研究[D]. 南京： 南京理工大学, 2012.

FANG Z M. Study on several problems of stability and optimal control of switched Systems[D]. Nanjing: Nanjing University of Science & Technology, 2012 (in Chinese).

Time-varyingformationcontrolofUAVswarmsystemswithswitchingtopologies

ZHOUShaolei*,QIYahui,ZHANGLei,YANShi，KANGYuhang

DepartmentofControlEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China

Trajectorytrackingandtime-varyingformationcontrolofunmannedaerialvehicle(UAV)swarmsystemswithswitchinginteractiontopologiesareinvestigated.TheUAVismodelledbyasecond-orderintegratorsystem.Basedontheconsensusmethod,protocolsareproposedtotransformtheformationproblemintoastabilityproblem.Theaveragedwelltimeofswitchingtopologiesisintroduced,andanalgorithmforthedesignofthegainmatrixoftheprotocolisgivenbysolvingalinearmatrixinequality(LMI).ItisprovenbyconstructingapiecewisecontinuousLyapunovfunctionthatthetrajectorytrackingandtime-varyingformationcanbeachievedbytheprotocolproposed.SimulationofaswarmsystemconsistingoffourUAVsmovinginthethreedimensionalspaceisconducted,andsimulationresultsdemonstratethatthetrajectorytrackingandtime-varyingformationforUAVswithswitchingtopologiescanbesolvedbythemethodproposed.

unmannedaerialvehicle;swarmsystem;switchingtopology;consensus;formationcontrol;trajectorytracking

2016-05-19；Revised2016-06-07；Accepted2016-07-18；Publishedonline2016-07-221149

URL：www.cnki.net/kcms/detail/11.1929.V.20160722.1149.002.html

.E-mailzhouslsd@sina.com

2016-05-19；退修日期2016-06-07；录用日期2016-07-18； < class="emphasis_bold">网络出版时间

时间：2016-07-221149

www.cnki.net/kcms/detail/11.1929.V.20160722.1149.002.html

＊

.E-mailzhouslsd@sina.com

周绍磊， 祁亚辉， 张雷， 等． 切换拓扑下无人机集群系统时变编队控制J． 航空学报,2017,38(4):320452.ZHOUSL,QIYH,ZHANGL,etal.Time-varyingformationcontrolofUAVswarmsystemswithswitchingtopologiesJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):320452.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0219

V249.122

A

1000-6893(2017)04-320452-09

(责任编辑： 张玉)