相关色噪声下无冗余累积量稀疏表示DOA估计

1 信号模型

X(t)=A(θ)S(t)+N(t)t=0,1,…,T-1

(1)

式中：X(t)=[x1(t)x2(t) …xM(t)]T，为M个阵元的接收信号，(·)T表示转置；S(t)=[s1(t)s2(t) …sK(t)]T，为信号向量；A(θ)=[a(θ1)a(θ2) …a(θK)]，为阵列流型矩阵，其第k列代表第k个信号的导向矢量为

a(θk)=[1 e-j2πdsin θk/λ… e-j2π(M-1)dsin θk/λ]T

(2)

假设噪声N(t)服从高斯分布，为圆对称、零均值的相关色噪声，且与信号相互独立，如文献[18-19]有

E{N(t)}=0

E{N(t1)NH(t2)}=δt1t2Rn

E{N(t1)NT(t2)}=0

式中：E(·)表示期望；(·)H表示共轭转置；δt1t2为Kronecker符号函数；Rn为一个M×M的正定Hermitian矩阵，表征其空间噪声的相关性。

2 基于均匀线阵的1维DOA估计算法

2.1 四阶累积量

在传统的阵列信号处理中，二阶统计量能够充分地利用高斯信号的信息进行DOA估计。然而，在大部分的通信系统中采用的是非高斯信源，如BPSK、QPSK和QAM等调制信号，对于非高斯信号，二阶统计量不能完全表征其统计特性，其大量有价值的统计信息包含在高阶统计量中，因此，常用四阶累积量进行处理。对于均匀线阵，根据零均值平稳随机过程的四阶累积量对称定义方式[7]，阵列接收数据的四阶累积量为

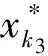
(3)

R4((k1-1)M+k2,(k3-1)M+k4)=

C4x(k1,k2,k3,k4)=

E{(X⊗X*)(X⊗X*)H}-

E{(X⊗X*)}E{(X⊗X*)H}-

E{(XX)H}⊗E{(XXH)*}

(4)

式中：⊗表示Kronecker积。信号的四阶累积量矩阵为

E{(S⊗S*)}E{(S⊗S*)H}-

E{(SS)H}⊗E{(SSH)*}

(5)

(6)

(7)

Cs=diag(γ1,γ2,…,γk)

由此，式(6)可以相应地简化为

R4=(A⊙A*)Cs(A⊙A*)H=

(8)

式中：

[a(θ1)⊗a*(θ1)a(θ2)⊗a*(θ2) …

a(θK)⊗a*(θK)]

(9)

2.2 四阶累积量快速去冗余

对于均匀线阵，在阵列孔径扩展过程中，产生了重叠的虚拟阵元，也就是形成了大量的冗余数据。这样，直接利用式(8)构造冗余字典来进行稀疏求解的计算量是巨大的。那么，可以构造一个M2×(2M-1)维的选择矩阵H，将四阶累积量矩阵R4中冗余的虚拟阵元剔除，使其维数降低。矩阵H可以表示为

式中：

Hm=

(10)

其中：IM为M维单位阵，定义(2M-1)×(2M-1)维矩阵G，即

G=HTH=diag(1,2，…,M-1,M,M-1,…,1)

同时，根据文献[20]，有

(11)

(12)

再结合矩阵H和G对式(12)作线性处理，去除冗余项，以降低矩阵R4的维数，可以得到

(13)

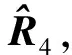
(14)

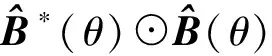
(15)

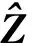
(16)

(17)

式(17)是与观测模型式(1)类似的一种新的观测模型，B(θ)为新的阵列流型矩阵，称为虚拟阵列流型，其维数为4M-3，大于阵元数M，进一步扩展了阵列孔径[14,20]，并且没有重叠虚拟阵元，这意味着通过降维运算得到的观测模型统计性能更优。

2.3 无冗余累积量稀疏表示及求解

利用2.2节所给出的算法得到新阵列导向矢量来构造完备的冗余字典，假设集合

表示空间可能存在的波达方向，于是整个空间所形成的流型矩阵为

它包含了所有可能的信号方位信息，则式(17)可以表示为

(18)

(19)

(20)

2.4 正则化参数选择

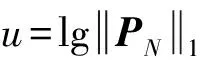
(21)

L-曲线上曲率最大的那点对应的λt值是L-曲线的最优值。

2.5 可分辨信源数分析

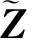
2.6 计算量分析

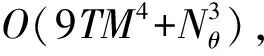
3 基于L型阵列的2维DOA估计方法

在实际应用中，信号往往是处于3维的立体空间中，很明显，采用2维DOA估计能够获得更多开发信道的空间信息，可以更加准确地估计来波信号的空间特征，更切合实际应用。将上述无冗余累积量稀疏表示的1维DOA估计推广到L型阵列2维DOA估计，扩展其应用范围。假设K个远场窄带非高斯信号入射到2M-1的L型均匀阵列上，阵元数为M的子阵X位于x轴上，阵元数为M的子阵Y位于y轴上，原点为o。第k个信号的入射方向为(θk,φk)，其中θk是入射信号的方位角(与第1节定义相同)，为入射信号在xoy平面的投影与x轴正方向的夹角，φk为俯仰角，为入射信号与其在xoy平面投影的夹角。这样，两子阵信号观测模型可以表示为

(22)

式中：Ax(θ,φ)和Ay(θ,φ)分别为两子阵的流型矩阵，对应的导向矢量分别为

(23)

利用稀疏表示的方法进行2维DOA估计时，冗余字典要覆盖整个2维空间，字典非常长，导致稀疏求解的计算量极其巨大。为了降低冗余字典的长度，利用空间角构造字典，将字典2维空间降为1维空间，大大减少了冗余字典的长度[24]。引入空间角α和β，分别表示为入射信号与x轴和y轴的夹角，由几何位置关系可得

(24)

将式(24)代入式(23)可得

(25)

根据式(8)，设子阵X和Y的四阶累积量分别为R4x和R4y，同理，对矩阵R4x和矩阵R4y进行二次降维和矢量化运算，可以得到与式(17)类似的最终向量观测模型：

(26)

式中：Bx(α)与By(β)为二维空间中最终的阵列流型矩阵，对应的导向矢量分别为

bx(αk)=[e-j2π(2M-2)dcos αke-j2π(2M-3)dcos αk… ej2π(2M-2)dcos αk]T

by(βk)=[e-j2π(2M-2)dcos βke-j2π(2M-3)dcos βk… ej2π(2M-2)dcos βk]T

(27)

利用式(27)阵列导向矢量来构造完备字典，将式(26)转化为稀疏表示问题，同时将对应的信号矢量扩展为N×1维的矢量PNx和PNy，PNx和PNy中非零元素分别代表空间角α和β的值。这样，基于L型均匀阵列的DOA估计问题可以表示为l1范数优化问题：

(28)

针对2维DOA估计问题，需要解决的一个难点就是方位角和俯仰角的配对问题。然而，通过稀疏分解不仅能得到信号的角度估计，还能得到信号的幅值，这样，可以利用相同信号的幅值相等这一特性进行配对，且利用估计出的空间角α和β，可以反推得到θ和φ：

很明显，在利用幅度信息进行L型阵列空间角配对时，会存在相近的难以判别的情况。在信号幅度特别相近时，可以利用两个空间角之间的数学关系cos2α+cos2β≤1进行约束[24]。在对空间角进行配对时，只有满足cos2α+cos2β≤1才作为同一信号的DOA信息，这样，解决了幅度相近信号的角度配对问题。

4 仿真与分析

通过仿真验证本文所提方法的估计性能。仿真中均采用均匀线阵，阵元间距d=λ/2，假设信源为独立远场窄带非高斯信号，仿真中采用4QAM调制信号。噪声均为服从高斯分布的相关色噪声，与信号独立，噪声协方差矩阵的第(k,l)个元素为

Rn(k,l)=σ2γ|k-l|ejπ(k-λ)/2

式中：噪声功率σ2用来调整信噪比的值，定义SNR=10×lgσ-2，γ为回归系数，调整噪声之间的相关性。γ越大，相关性越强，而γ=0时噪声为白高斯噪声。另外，均方根误差定义为

仿真1：假设6个独立4QAM信号入射到阵元数为4的均匀线阵, 信号入射方向为

[-40° -25° -10° 5° 20° 35°]

信噪比为10 dB，快拍数为500，噪声相关系数γ设为0.7。图1为基于上述条件下式(21)的L-曲线，根据图中曲率最大点可以得到对应的最优正则化参数λt=0.29。MUSIC-like和本文算法空间谱如图2所示。可以看出，本文算法和MUSIC-like算法均能估计出多于物理阵元数的信源数，但本文算法无需预知信源数目，且具有尖锐的谱峰，分辨率更高。

仿真2：考虑2个独立信源，入射方向为θ1=-13°,θ2=30°，线阵的阵元数为4，快拍数为500，γ设为0.9，同样，利用式(21)，后续所有仿真中λt均取0.42。图3为不同算法均方根误差随信噪比变化关系。可以看出，由于L1-ACMSR[14]算法是基于二阶统计量阵列协方差矩阵稀疏表示的DOA估计算法，受相关色噪声影响较大，因此估计误差最大；MUSIC-like算法虽然能抑制相关色噪声，但受本身算法性能的限制，估计精度也受限；文献[15]算法在四阶累积量的合成阵列协方差矩阵稀疏表示基础上，提出L1-SRFOC算法，估计精度在低信噪比下比MUSIC-like算法有所提高，但效果并不明显；而本文算法估计性能随着信噪比增大迅速上升，与其他方法相比，有着明显的优势，说明本文算法具有更好的估计精度和噪声鲁棒性。

图1 L-曲线
Fig.1 L-curve

图2 MUSIC-like和本文算法空间谱
Fig.2 Spatial spectra for MUSIC-like and proposed algorithm

图3 均方根误差随信噪比变化关系(1维DOA)
Fig.3 Variation relationship between root mean square error (RMSE) and signal to noise ratio (SNR) (1-dimensional DOA)

为验证本文所提算法的空间分辨能力，假设：以Θ=[θ1-δ,θ1+δ]∪…∪[θp-δ,θp+δ]为假设集合，δ为信噪比对应的均方根误差，[θp-δ,θp+δ]为第p个DOA区间。一次实验中，若估计出的DOA都能够落在它们自己的区间内，那么认为这次实验是成功的。如果进行了1 000次实验，只有Ns次实验中的所有DOA都能被成功分辨了，则分辨概率为Ns/1 000。图4中假设δ=1.5，其他仿真条件与图3一致，为不同算法的分辨概率随信噪比变化关系，与图3分析一致，L1-ACMSR算法受相关色噪声影响，误差较大，本文算法的分辨能力最好。

仿真3：验证本文所提算法受快拍数影响的大小，图5为不同算法均方根误差随快拍数变化关系，γ=0.9，信噪比设为10 dB，其他仿真条件与图3相同。很明显，与其他算法相比，本文算法优势突出，其均方根在低样本情况下较小，且随着快拍数增加呈下降的趋势，这表明了本文算法具有较好的估计性能，克服了传统四阶累积量算法受快拍数影响较大的缺陷。

图4 分辨概率随信噪比变化关系(1维DOA)
Fig.4 Variation relationship between resolution
probability and SNR (1-dimensional DOA)

图5 均方根误差随快拍数变化关系(1维DOA)
Fig.5 Variation relationship between RMSE and snapshot (1-dimensional DOA)

仿真4：假设入射信源为3个独立信号，方位角和俯仰角的入射角度分别为(99°,63°)，(120°,65°)，(249°,20°)，信噪比为10 dB，快拍数为500，噪声的相关系数γ取0.6。图6为本文算法2维角估计结果。可以看出，本文算法对3个信号的方位角和俯仰角得到较高准确度的估计，估计出来的结果分别为(99.39°,63.32°),(120.77°,65.59°),(248.12°,19.99°)。估计结果和实际DOA值基本重合，误差较小。

图6 本文算法2维角估计结果
Fig.6 Results of two-dimensional angle estimation with proposed algorithm

仿真5：考虑2个入射信号，入射角度分别为(θ1,φ1)=(60°,42°)，(θ2,φ2)=(185°,25°)。γ设为0.9。图7为快拍数为500条件下均方根误差随信噪比变化关系。可看出，受相关色噪声影响，文献[16]算法的均方根误差较大，但随着信噪比增大，受噪声影响不断减弱，当信噪比大于15 dB时，其估计性能优于MUSIC-like算法，而本文算法的均方根误差最小，且随信噪比增大明显下降，这展现了本文算法在2维DOA估计应用中亦能有效地抑制相关色噪声，具有较好的噪声鲁棒性和估计精度。

图8为不同算法的方位角和俯仰角分辨概率随信噪比变化的关系，仿真中取δ=1.2，其他仿真条件与图7一致。可以明显看出，在2维DOA估计中，文献[16]算法受相关色噪声影响，分辨能力较差，本文算法的分辨能力最好，充分地展示了所提算法具有较好的估计精度和分辨率。

图9为信噪比为10 dB条件下，不同算法的均方根误差随快拍数变化关系。受噪声影响，文献[16]算法均方根误差较大，而MUSIC-like算法作为传统四阶累积量算法，受快拍数影响较大，与1维DOA估计一致，本文算法在2维DOA估计情况下，仍能克服对快拍数的敏感性。

图7 均方根误差随信噪比变化关系(2维DOA)
Fig.7 Variation relationship between RMSE and SNR (2-dimensional DOA)

图8 分辨概率随信噪比变化关系(2维DOA)
Fig.8 Variation relationship between resolution probability and SNR (2-dimensional DOA)

图9 均方根误差随快拍数变化关系(2维DOA)
Fig.9 Variation relationship between RMSE and snapshot (2-dimensional DOA)

5 结论

1) 针对传统四阶累积量算法计算复杂度高、受快拍数影响大的问题，通过二次降维运算对四阶累积量快速去冗余，进而采用稀疏表示实现DOA估计，提高了估计精度和减弱了对快拍数的敏感性。

2) 在将方法扩展到L型阵列2维DOA估计时，通过空间角构造冗余字典，大大地降低了稀疏求解的复杂度，利用稀疏求解的信号幅度信息实现方位角和俯仰角配对。同时，该方法还适用于其他存在任意夹角的阵列，如平行线阵等。

[1] NAGESHA V, KAY S. Maximum likelihood estimation for array processing in colored noise[J]. IEEE Transactions on Signal Processing, 1996, 44(2): 169-180.

[2] LI M, LU Y, HE B. Array signal processing for maximum likelihood Direction-of-Arrival estimation[J]. Journal of Electrical & Electronic Systems, 2013, 3(1): 117.

[3] ZACHARIAH D, JANSSON M, BENGTSSON M. Utilization of noise-only samples in array processing with prior knowledge[J]. IEEE Signal Processing Letters, 2013, 20(9): 865-868.

[4] WERNER K, JANSSON M. Optimal utilization of signal-free samples for array processing in unknown colored noise fields[J]. IEEE Transactions on Signal Processing, 2006, 54(10): 3861-3872.

[5] PRASAD S, WILLIAMS R T, MAHALANABIS A K, et al. A transform-based covariance differencing approach for some classes of parameter estimation problems[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1988, 36(5): 631-641.

[6] YAN G, NING L, CHANG T, et al. Covariance differencing technique based DOA estimation method under hermitian symmetric Toeplitz noise[C]//Proceedings of IEEE Conference on Wireless Communications & Signal Processing. Piscataway： IEEE, 2012: 1-5.

[7] DOGAN M C, MENDEL J M. Applications of cumulants to array processing. I. aperture extension and array calibration[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1200-1216.

[8] SHAN Z L, JI F, WEI G. Extention music-like algorithm for DOA estimation with more sources than sensors[C]//Proceedings of IEEE Conference on Neural Networks & Signal Processing. Piscataway: IEEE, 2003: 1281-1284.

[9] JING X R, SUI W W, ZHOU W. DOA estimation of coherent signals based on fourth-order cumulant and temporal smoothing[J]. Systems Engineering and Electronics, 2012, 34(4): 789-794.

[10] LIAO B, CHAN S C. A cumulant-based approach for direction finding in the presence of mutual coupling[J]. Signal Processing, 2014, 104(12): 197-202.

[11] SHI H P, LENG W, WANG A G, et al. Fast orthonormal propagator direction-finding algorithm based on fourth-order cumulants[J]. Applied Computational Electromagnetics Society Journal, 2015, 30(6): 638-644.

[12] TIAN Y, XU H. Extended-aperture DOA estimation with unknown number of sources[J]. Electronics Letters, 2015, 51(7): 583-584.

[13] 窦道祥, 李茂, 何子述. 基于稀疏重建的MIMO-OTH雷达多模杂波抑制算法[J]. 航空学报, 2015, 36(7): 2310-2318.

DOU D X, LI M, HE Z S. Multi-mode clutter suppression algorithm of MIMO-OTH radar based on sparse reconstruction[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2310-2318 (in Chinese).

[14] HE Z Q, LIU Q H, JIN L N, et al. Low complexity method for DOA estimation using array covariance matrix sparse representation[J]. Electronics Letters, 2013, 49(3): 228-230.

[15] LI S, JIANG X, HE W, et al. Direction of arrival estimation via sparse representation of fourth order statistics[C]//Proceedings of IEEE Conference on Signal Processing, Communication and Computing (ICSPCC). Pisca-taway: IEEE, 2013: 1-4.

[16] LIU Q H, OUYANG S, JIN L N. Two-dimensional DOA estimation with L-shaped array based on a jointly sparse representation[J]. Information Technology Journal, 2013, 12(10): 2037.

[17] LIU Z. DOA and polarization estimation via signal reconstruction with linear polarization-sensitive arrays[J]. Chinese Journal of Aeronautics, 2015, 28(6): 1718-1724.

[18] QIAN C, HUANG L, XIAO Y H, et al. Localization of coherent signals without source number knowledge in unknown spatially correlated Gaussian noise[J]. Signal Processing, 2015, 111(6): 170-178.

[19] ZENG W J, LI X L, ZHANG X D. Direction-of-arrival estimation based on the joint diagonalization structure of multiple fourth-order cumulant matrices[J]. IEEE Signal Processing Letters, 2009, 16(3): 164-167.

[20] MA W K, HSIEH T H, CHI C Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: A Khatri-Rao subspace approach[J]. IEEE Transactions on Signal Processing, 2010, 58(4): 2168-2180.

[21] TIBSHIRANI R. Regression shrinkage and selection via the LASSO[J]. Journal of the Royal Statistical Society, 1996, 58(1): 267-288.

[22] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[23] HANSEN P C, O’LEARY D P. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503.

[24] 罗争, 吴林, 邵璐璐. 一种稀疏表示的二维DOA降维估计新算法[J]. 中国电子科学研究院学报, 2013, 8(5): 501-506.

LUO Z, WU L, SHAO L L. A novel two-dimensional direction-of-arrival degradation estimation based on sparse signal representation[J]. Journal of CAEIT, 2013, 8(5): 501-506 (in Chinese).

DOAestimationusingnon-redundantcumulantssparserepresentationincorrelatedcolorednoise

LIUQinghua*,ZHOUXiuqing,JINLiangnian

GuangxiExperimentCenterofInformationScience,GuilinUniversityofElectronicTechnology,Guilin541004,China

Thispaperaimsattheproblemthatconventionalfourth-ordercumulantshavehighcomputationalcomplexityandaresensitivetodatasamples.Anewdirectionofarrival(DOA)estimationmethodisproposedtoeliminatetheredundancyquickly.Themassiveredundantdataareremovedbyselectionmatrixtoreducethedimensionoffourth-ordercumulantsmatrix.Byvectorizingthenon-redundantcumulantsmatrixandreducingthedimensionagain,thevectormeasurementmodelwithbetterstatisticalperformanceisthenobtained.Thesparserepresentationofthemeasurementmodelcorrespondingtotherelatedover-completebasisisconstructedforDOAestimation.ThenthemethodisextendedtoLarrayfortwodimensionalDOAestimation.Comparedwithconventionalfourth-ordercumulantsmethods,theproposedmethodcangreatlyreducethecomputationalcomplexityandtheimpactofthesizeofdatasamples,andcanefficientlysuppresscorrelatedcolorednoise.TheoreticalanalysisandsimulationexperimentsverifythattheproposedmethodhashigherresolutionandbetterestimationaccuracyforoneandtwodimensionalDOAestimation.

directionofarrival(DOA)estimation;fourth-ordercumulant;sparserepresentation;correlatedcolorednoise;non-redundancy

2016-04-19；Revised2016-04-20；Accepted2016-07-13；Publishedonline2016-09-051643

URL：www.cnki.net/kcms/detail/11.1929.V.20160905.1643.004.html

s：NationalNaturalScienceFoundationofChina(61461012,61371186)；GuangxiKeyLaboratoryofWire-lessWidebandCommunication&SignalProcessing(GXKL06160110)；CenterforCollaborativeInnovationintheTechnologyofIOTandtheIndustrialization(WLW20060205)；InnovationProjectofGUETGraduateEducation(2016YJCX87).

2016-04-19；退修日期2016-04-20；录用日期2016-07-13； < class="emphasis_bold">网络出版时间

时间：2016-09-051643

www.cnki.net/kcms/detail/11.1929.V.20160905.1643.004.html

国家自然科学基金 (61461012,61371186)；广西无线宽带通信与信号处理重点实验室基金 (GXKL06160110)；广西物联网技术及产业化推进协同创新中心资助项目 (WLW20060205)；桂林电子科技大学研究生教育创新计划 (2016YJCX87)

＊

.E-mailliuqinghuagl@126.com

刘庆华，周秀清，晋良念．相关色噪声下无冗余累积量稀疏表示DOA估计J．航空学报,2017,38(4):320331.LIUQH,ZHOUXQ,JINLN.DOAestimationusingnon-redundantcumulantssparserepresentationincorrelatedcolorednoiseJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):320331.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0247

V243.2； TN911.7

1000-6893(2017)04-320331-10

(责任编辑：苏磊)

＊Correspondingauthor.E-mailliuqinghuagl@126.com