考虑专家风险偏好的区间直觉模糊多属性决策方法

张卫国++李鹏斐++刘勇军

摘要： 针对决策信息为区间直觉模糊数且属性权重未知的多属性决策问题，提出了考虑专家风险偏好的决策方法。该方法基于专家对风险的偏好程度，构建了一种新的得分函数（P-λ记分函数），据此提出一种区间直觉模糊属性熵权法。同时，定义了考虑专家风险偏好的区间直觉模糊数相关系数，并构造备选方案与理想方案和临界方案属性值相关系数矩阵。然后，集结属性权重和矩阵信息，计算出各种风险偏好情形下的相对贴近度值并得到方案集的综合排序结果。最后，通过算例分析来阐明该方法的有效性。

关键词： 专家风险偏好；P-λ记分函数；区间直觉模糊集相关系数；熵权法

中图分类号： C934文献标志码：A文章编号：1009-055X（2017）05-0027-11

doi：1019366/jcnki1009-055X201705004

一、引言

经济学、工程學和信息科学等领域中的决策问题大多具有复杂性和高度的模糊性。经典的模糊集理论在实践中因表达的内蕴信息较少而受到了众多限制，对此Atanassov[1]提出了直觉模糊集理论，定义了隶属度、非隶属度和犹豫度3个概念。为解决隶属度与非隶属度等信息有时无法用准确实数值来刻画的问题，Atanassov和Gargov[2]进一步推广了直觉模糊集，定义了区间直觉模糊集的概念，并且定义了区间直觉模糊集的一些基本运算法则。区间直觉模糊集的优点是隶属度和非隶属度均为区间值，可以更加灵活地刻画模糊性，所以相关理论也常常被用来解决投资评价[3]、企业ERP系统选择[4]等多属性决策问题。

目前部分学者围绕着直觉模糊决策中的属性权重不确定决策、相似性测度理论以及得分函数的构建方法来展开研究并取得了一些成果。属性权重不确定决策研究方面，Luo和Wei[5]建立了基于最小误差原则的直觉模糊信息优化模型，求取了属性值权重。Qian和Xu[6]针对属性权重不确定情形下的多准则决策问题，基于理想点法构建了3个优化模型，通过求解模型得到属性的客观权重。杨威等[7]采用区间直觉模糊不确定语言变量建模不确定信息，然后利用最大偏差法建立一个线性规划模型来计算西安地铁壁画的权重向量。Xu和Zhang[8]基于极大偏差法来确定准侧的权重大小，并给出了根据犹豫模糊信息的TOSIS决策方法。Chen和Yang[9]基于约束模糊AHP方法，根据FTOPSIS对方案集进行了比较。李艳玲等[10]研究了区间直觉模糊数的几何意义，基于熵值最大化原理，求出导弹技术相关指标的权重。

直觉模糊集的相似性测度研究方面，Gerstenkorn和Manko[11]为了反映方案之间的相似程度，提出了直觉模糊集的关联测度函数和相关系数的公式。Bustince和Burillo[12]定义了区间直觉模糊集的近似度的度量。Xu[13]给出了一种新的直觉模糊集关联公式，并推广到区间直觉模糊集理论，且把此方法应用到了医疗领域。Xu[14]从集合论的角度进行考虑，并给出了一种基于集合论的直觉模糊集关联系数。Xu[15]提出了基于距离测度的区间直觉模糊矩阵群决策方法，但由于距离测度本身的缺点及犹豫度的缺失导致存在内蕴信息利用不完备的问题。Khalid 和Abbas [16]定义了一个基于Hausdorff距离的直觉模糊软集的相似性测度，并把这个应用推广到了医疗诊断。Xu和Zhang[17]考虑了MADM问题中犹豫模糊集的问题，提出了一个改进的基于TOPSIS和极大利差法来解决MADM的模型。Liao等[18]指出了目前犹豫模糊集相关系数的不足，定义了一个新的相关系数公式。

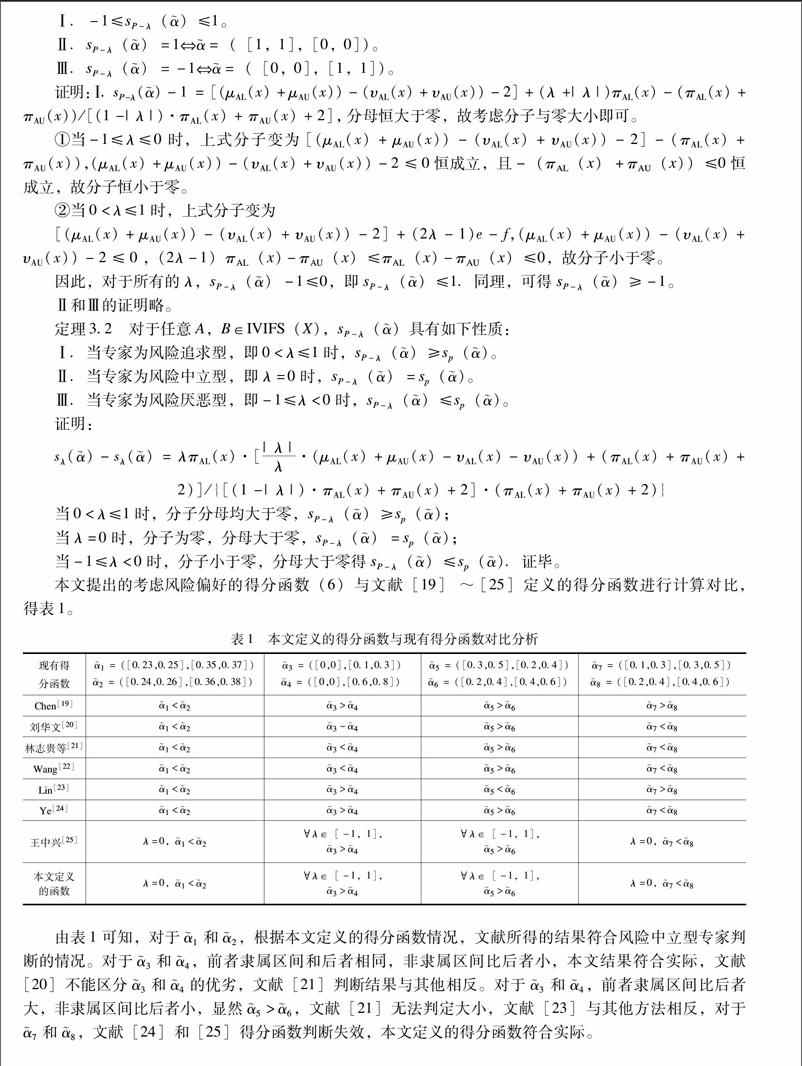
直觉模糊集的得分函数构建研究方面，Chen 和 Tan [19]从隶属度μA和非隶属度υA出发，提出得分函数和精确函数分别为SA=μA-υA，HA=μA+υA。刘华文[20]考虑到犹豫的投票人会受到他人影响，将犹豫度πA按照比例划分为μAπA（μA为隶属度、υAπA（υA为非隶属度）和（1-μA-υA）πA三部分，提出SA=μA（1+πA）。林志贵等[21]等认为犹豫部分会减小得分函数，给出得分函数SA=μA-πA=2μA+υA-1。Wang等[22]提出S（A）=（3μA-υA-1）/2。Lin等[23]综合考虑了得分函数和精确函数，定义得分函数为S（A）=μA/2+3/2（1-πA）-1。Ye[24]认为划分后的犹豫部分（1-μA-υA）πA对得分函数产生负向影响，得到得分函数SA=μA（1+πA）-π2A。王中兴等[25]定义了排序直觉模糊数的含风险参数的得分函数，得到Sλ（A）=（μA-υA）（1+πA）+λπ2A。

综上所述，此前学者们较少地考虑到决策专家对犹豫度风险偏好不同会对区间直觉模糊集得分函数、属性熵以及相似性测度的产生怎样的影响，目前此方面的研究相对缺乏。在实际决策问题中，由于专家知识、数据和经验等方面的差异，决策专家往往具有较强的主观意愿，对犹豫度信息的偏好程度会有所不同，因而会对同一个区间直觉模糊数得分函数值的大小、区间直觉模糊数的相似值的判断存在差异。此外，由于在决策系统中，不同方案集在某一属性下模糊数的得分函数值的差异程度反映了该属性的信息熵。熵值越大，属性的差异程度越大，从而该属性对综合评价的影响也越大，则该属性的权重也越大。因此，决策者对风险偏好不同会导致得分函数大小的不同，进而导致属性权重大小的不同。鉴于此，本文基于不同专家对同一个决策问题会有不同的风险态度这一客观情况，引入风险偏好系数λ来刻画决策者对犹豫度信息的不同偏好，定义了考虑决策风险的区间直觉模糊数得分函数公式和相关系数公式，并基于得分函数提出了熵权法来求取属性权重；根据对风险追求程度越大或对风险规避程度越大、专家权重越小的原则，确定不同风险类型专家的权重，提出了完整的区间直觉模糊集的综合排序方法。本文从决策专家对风险的态度、直觉模糊集相似性测度等视角构建排序方法，为属性权重未知的区间直觉模糊决策理论的应用提供理论依据。endprint

六、结语

[HJ5mm][HJ][HT]

传统的区间直觉模糊集排序研究较少探讨决策者具有风险偏好的情况，本文以区间直觉模糊集环境下决策者具有风险偏好的决策问题为背景，主要做了以下几方面工作：

（1）提出了考虑专家风险偏好的得分函数。该函数从决策者角度量化了犹豫部分对决策结果的影响，通过引入风险参数λ来量化专家的风险偏好程度。

（2）提出了考虑专家风险偏好的相关系数。该系数公式来源于向量夹角的思想，在考虑不同风格专家对犹豫度偏好不同的基础上，引入了专家对风险的偏好系数λ来对原隶属度区间和非隶属度进行拓展。

（3）根据考虑专家风险偏好的得分函数，提出了属性权重熵权法。某一属性下各方案集区间直觉模糊数的得分函数的绝对值的离散程度反映了其模糊的程度，故从得分函数出发计算各属性的平均信息熵，进而计算出相关属性的权重值。

（4）通過算例分析并与已有文献比较，得到本文决策方法的优越性。

综合来看，此决策方法可以较好地刻画出专家风格，λ的引入较好地量化了专家对风险的偏好程度，熵权法的引入也解决了其他方法过于依赖专家主观判断的缺点，相关系数方法的应用克服了传统基于距离测度的理论缺陷，减少了犹豫度信息的损失，专家权重的二次集结也保证了评价方法的说服力，避免单一专家评价的偏颇。方法适用性较广，具有可推广性。

参考文献：

[1]ATANASSOV K Intuitionistic Fuzzy sets [J] Fuzzy Sets and Systems， 1986， 20（1）： 87-96

[2]ATANASSOV K， GARGOV G Interval-valued Intuitionistic Fuzzy sets [J] Fuzzy Sets and Systems， 1989， 31（3）： 343-349.

[3]高明美，孙涛，朱建军. 基于改进熵和新得分函数的区间直觉模糊多属性决策[J]. 控制与决策， 2016， 31（10）： 1757-1764.

[4]梁昌勇，戚筱雯，张俊岭，等. 基于诱导型区间直觉模糊混合算子的群决策方法[J]. 系统工程学报， 2012， 27（6）：759-771.

[5]LUO Y J， WEI G W. Multiple Attribute Decision Making with Intuitionistic Fuzzy Information and Uncertain Attribute Weights Using Minimization of Regret [C]. Xian：2009 4th IEEE Conference on Industrial Electronics and Applications，2009： 3720-3723.

[6]QIAN G， XU Z S. Three Optimization Models Based on Ideal Points for Uncertain Multi-attribute Decision Making [J]. Systems Engineering and Electronics， 2003， 25（5）： 517-519.

[7]杨威， 庞永锋， 史加荣. 不完全权重信息的区间直觉模糊不确定语言TOPSIS方法[J]. 模糊系统与数学， 2015（2）：125-131.

[8]XU Z S， ZHANG X L. Hesitant Fuzzy Multi-attribute Decision-making Based on TOPSIS Within Complete Weight Information[J]. Knowledge-Based Systems， 2013， 52（6）： 53-64.

[9]CHEN Z P， YANG W. An MAGDM Based on Constrained FAHP and FTOPSIS and Its Application to Supplier Selection[J]. Mathematical and Computer Modelling， 2011， 54（11）： 2802-2815.

[10]李艳玲， 殷新丽， 杨剑. 区间直觉模糊决策中专家与属性权重确定方法[J]. 计算机工程与应用， 2016， 52（18）： 158-161.

[11]GERSTENKORN T， MANKO J. Correlation of Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems， 2007，17（4）： 39-43.

[12]BUSTINCE H， BURILLO P. Correlation of Interval-valued Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems， 1995， 74（2）：237-244.

[13]XU Z S. On Correlation Measures of Intuitionistic Fuzzy Sets [J]. Lecture Notes in Computer Science， 2006（4224）：16-24.

[14]XU Z S. Some Similarity Measures of Intuitionistic Fuzzy Sets and Their Applications to Multiple Attribute Decision Making [J]. Fuzzy Optimization and Decision Making， 2007， 6（2）：109-121.endprint

[15]XU Z S. A Method Based on Distance Measure for Interval-valued Intuitionistic Fuzzy Group Decision Making[J]. Information Sciences， 2010， 180（1）：181-190.

[16]KHALID A， ABBAS M. Distance Measures and Operations in Intuitionistic and Interval Valued Intuitionistic Fuzzy Soft Set Theory [J]. International Journal of Fuzzy Systems，2015，17（3）：490-497.

[17]XU Z S， ZHANG X L. Hesitant Fuzzy Multi-attribute Decision Making Based on TOPSIS with Incomplete Weight Information [J]. Knowledge-Based Systems， 2013， 52（6）：53-64.

[18]LIAO H C， XU Z S， ZENG X J. Novel Correlation Coefficients Between Hesitant Fuzzy Sets and Their Application in Decision Making [J]. Knowledge-Based Systems， 2015， 82（C）：115-127

[19]CHEN S M， TAN J M. Handling Multi-criteria Fuzzy Decision-making Problems Based on Vague Set Theory[J]. Fuzzy Sets and Systems， 1994，67（2）：163-172.

[20]刘华文. 多目标模糊决策的Vague集方法[J]. 系统工程理论与实践， 2004， 24（5）：103-109.

[21]林志貴，徐立中，王建颖. 基于Vague集的多目标模糊决策方法[J]. 计算机工程， 2005， 31（5）：11-13.

[22]WANG J， ZHANG J， LIU S Y. A New Score Function for Fuzzy MCDM Based on Vague Set Theory[J]. International Journal of Computational Cognition， 2006， 4（1）：44-48.

[23]LIN L， YUAN X H， XIA Z Q. Multicriteria Fuzzy Decision-making Methods Based on Intuitionistic Fuzzy Sets[J]. Journal of Computer and System Sciences， 2007， 73（1）：84-88.

[24]YE J. Using An Improved Measure Function of Vague Sets for Multicriteria Fuzzy Decision-making[J]. Expert Systems with Applications，2010， 37（6）：4706-4709.

[25]王中兴，罗雪鹏. 基于决策者风险偏好的直觉模糊数排序方法[J]. 模糊系统与数学， 2014， 28（6）：129-136.

[26]高建伟， 刘慧晖， 谷云东. 基于前景理论的区间直觉模糊多准则决策方法[J]. 系统工程理论与实践， 2014， 34（12）：3175-3181.

[27]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J]. 控制与决策， 2007， 22（2）：215-219.

[28]PARK D G， KWUN Y C， PARK J H， et al. Correlation Coefficient of Interval-valued Intuitionistic Fuzzy Sets and Its Application to Multiple Attribute Rroup Decision Making Problems[J]. Mathematical and Computer Modelling， 2009， 50（10）： 1279-1293.

[29]袁宇， 关涛， 闫相斌， 等. 基于区间直觉模糊数相关系数的多准则决策模型[J]. 管理科学学报，2014，17（4）：11-18.

[30]GRZEGORZEWSKI P. Distances Between Intuitionistic Fuzzy Sets And/or Interval-valued Fuzzy Sets Based on the Hausdorff metric [J]. Fuzzy Sets and Systems， 2004， 148（2）：319-328.

[31]吴冲，万翔宇. 基于改进熵权法的区间直觉模糊TOPSIS方法[J]. 运筹与管理， 2014， 23（5）：42-47.

[32]SHANNON C E. A Mathematical Theory of Communication [J]. Bell Sys Tech， 1948， 27（3）： 379-423.

[33]WEI G W. Gray Relational Analysis Method for Intuitionistic Fuzzy Multiple Attribute Decision Making[J]. Expert Systems with Applications， 2011， 38（9）： 11671-11677.endprint