Origin软件在中学物理实验教学中的应用研究——以“探究功与速度变化的关系”实验教学为例

陈志军

(安徽省绩溪中学 安徽 宣城 245300)

教育技术应用

Origin软件在中学物理实验教学中的应用研究
——以“探究功与速度变化的关系”实验教学为例

陈志军

(安徽省绩溪中学 安徽 宣城 245300)

利用Origin软件对“探究功与速度变化的关系”的实验数据进行多项式拟合、自定义函数y=Ax2拟合和线性拟合，并进行对比分析，将现代信息技术辅助中学物理实验教学，以提高学生实验数据处理和实验探究能力，落实科学精神、科学思维、实践创新、技术应用等核心素养．

功与速度变化 信息技术 科学思维 核心素养

推进信息化教学，将现代信息技术用于辅助物理教学和解决物理实际问题，推动教学手段、教学方法，特别是物理实验教学的信息化，可有效改变学生的学习方式和探索方法，激发学生的探索精神，培养学生观察、分析、综合、推理等能力，促进学生创造性思维的训练和实验能力的提高，有效推动科学精神、科学思维、实践创新、技术应用等核心素养的落实．

Origin Pro 8.0 是Origin Lab公司研发的专业绘图和数据分析软件，其简单易学、操作灵活、功能强大，满足制图、数据分析、函数拟合的需求，为数据分析提供了各种各样的工具，适合科学研究、工程设计、教学等．在数据分析上，该软件基于最小二乘法为基础的线性回归分析，可以高效准确地拟合出线性关系变量的直线方程，同时给出斜率k和截距b的值，包括误差值和校正决定系数(相似度)等数据，能为改进中学物理实验教学提供帮助，可有效地解决中学物理实验中利用线性变量关系处理测量数据的实验，如利用单摆测重力加速度、利用匀变速直线运动测加速度、利用机械能守恒测重力加速度、探究弹簧弹力与弹簧伸长的关系、测定电源电动势和内阻等实验．该软件不仅可以给出线性关系的直线拟合方程，还可以进行多项式和自定义函数进行拟合，给出方程及各项系数、误差分析、方程校正决定系数等．本文以“探究功与速度变化的关系”实验教学为例，运用Origin Pro 8.0软件对该实验数据的多项式拟合、自定义函数拟合和直线拟合的方程进行对比分析研究．

1 实验原理与方法

采用如图1所示实验装置探究力对物体做功与物体速度变化的关系．让橡皮筋拉动小车做功使小车的速度增加，调节拉小车的橡皮筋的条数由1条变为2条、3条……每条橡皮筋对物体做功为W0，则橡皮筋对小车做的功依次为W0，2W0，3W0，…通过对打点计时器所打纸带的测量，可计算得出每次实验后小车的速度，分析每次橡皮筋所做的功与小车获得速度的关系，即可总结出功与速度的关系．

图1 探究力对物体做功与物体速度变化关系实验装置

实验时要先平衡摩擦力，尽量选择相同的橡皮筋(用市场上的加长扎发橡皮筋，用传感器多次变换拉力，保证每条橡皮筋受力变化情况相同)，并保证橡皮筋拉伸的长度都和第一次相同，让小车从同一位置由静止释放，测得的速度v，v2和对应的橡皮筋条数n记入下面表格，分析实验数据，探究橡皮筋所做功W(W=nW0)与v，v2的关系．

表1测得的实验数据

n(=W/W0)0123456v/(m·s-1)00.851.111.451.621.762.06v2/(m2·s-2)00.7231.2322.1032.6243.0984.244

2 Origin软件对实验数据的分析教学

2.1多项式拟合

将以上表格数据导入Origin Pro软件，以橡皮筋的条数n为纵坐标，每次实验测得的速度v为横坐标，得到如图2所示的n-v散点图，由图可以看出，橡皮筋的条数变化并不是线性关系，尝试用线性拟合，误差非常大．考虑到数据的非线性变化，根据函数的性质和散点分布走势，首先选择多项式拟合．

图2 n-v散点图

在Origin Pro软件中选择多项式拟合“Fitting Polynomial”，确定拟合后得到如图3所示的曲线和数据，拟合方程为n=1.339v2+0.287v-0.046，校正决定系数达到98.50%，从各项系数真实值的标准差来看，一次项系数B1和常数项误差非常大，而二次项系数B2误差不大，该拟合存在局限性．

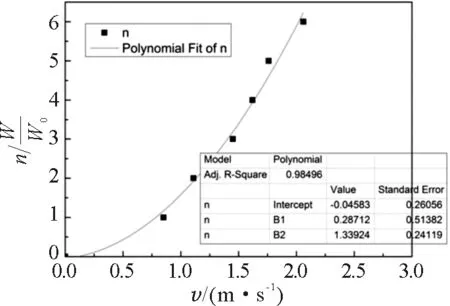
图3 多项式拟合

2.2自定义函数y=Ax2进行拟合

考虑到多项式拟合时，一次项系数B1和常数项误差过大，而二次项系数B2误差并不大，因此，该拟合可以考虑只取二次项进行自定义函数拟合．

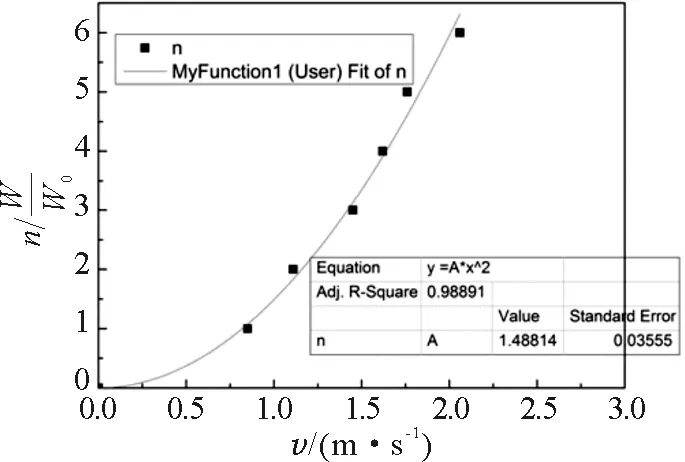
图4 函数拟合

2.3线性拟合

在数据计算时，v2的值已经计算填入表中，在Origin Pro软件中，以橡皮筋的条数n为纵坐标，以v2为横坐标，做出n-v2变化的散点图，选择“Fitting linear”得到线性拟合的曲线如图5所示，曲线方程为

n=1.468v+0.060

校正决定系数达到98.70%，斜率真实值的标准差仅为0.069，相对误差比较小，常数项0.060与n值比较太小，完全可以忽略，可以确定橡皮筋的条数n与速度v2成正比例变化关系，关系式为n=1.468v2．同样，由于每条橡皮筋对物体做功均为W0，所以

W=nW0=1.468W0·v2=k′v2

其中k′=1.468W0，即每次橡皮筋对小车所做的功W与小车速度的二次方成正比．

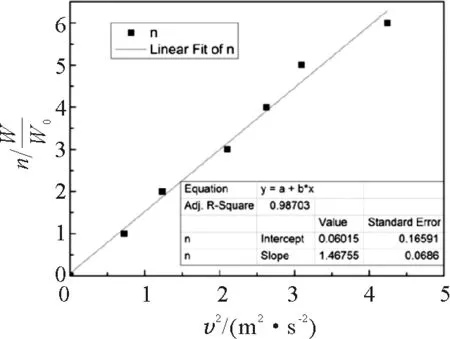
图5 n-v2线性拟合

在拟合过程中，从自定义的二次函数拟合和直线拟合，得到n对v的二次函数拟合方程为

W=kv2

其中k=1.488W0，而n对v2的直线拟合方程为W=k′v2，其中k′=1.468W0．可以看出k和k′的值非常接近，拟合效果非常好，而二项式拟合的二次项系数为1.339W0，与自定义的二次函数拟合以及直线拟合的系数相差比较大，因此可以分析得出自定义函数y=Ax2拟合和线性拟合结果的一致性，可确定

W∝v2，即橡皮筋对小车所做的功W与小车的速度的平方成正比．

3 结论

(1) 运用Origin Pro 8.0软件对该实验数据的多项式拟合、自定义函数拟合和直线拟合的结果进行对比分析研究，引导学生熟悉和掌握科学研究常用的数据分析软件Origin的使用，提高学生实验数据处理能力和实验探究能力，有效调动学生学习的积极性和科学研究的兴趣．

(2)通过自定义函数拟合和直线拟合的对比分析研究，分析得出自定义函数y=Ax2拟合和线性拟合结果的一致性，可确定W∝v2，加深了学生对对比分析等科学思维方法的运用，锻炼学生观察、分析、综合、逻辑推理等能力，有助于培养学生求真务实的科研态度和严谨的科研精神，推动学生科学精神、科学思维、实践创新、技术应用等核心素养的发展．

2017-02-11)