浅谈牛顿定律与参考系

胡 敏 郭长江 顾 锋

(上海师范大学数理学院 上海 200234)

浅谈牛顿定律与参考系

胡 敏 郭长江 顾 锋

(上海师范大学数理学院 上海 200234)

对牛顿定律与参考系之间的关系作简要的梳理．首先，由牛顿第一定律着手，分析惯性参考系与非惯性参考系的本质区别．再基于对牛顿第二定律的理解，从“F=m(a相+a参)”与“F-ma参=ma相”两式的区别与联系出发分析惯性参考系与平动非惯性参考系的关系，并对转动非惯性参考系中各惯性力的物理意义作展开解释．最后，指出牛顿第三定律与参考系的选取无关．

牛顿定律 惯性参考系 非惯性参考系 惯性力

在中学物理教学中，通常选取地球当做参考系，忽视了参考系在经典力学中的重要作用．在讨论牛顿运动定律时，学生往往会出现很多混淆不清的问题．

针对此现状，本文对牛顿定律与参考系之间的关系作简要梳理，并从牛顿第二定律的定量表达式出发对非惯性系中的各惯性力作展开解释．

1 牛顿第一定律与参考系

在力学中，根据牛顿定律是否成立将参考系分为了惯性参考系和非惯性参考系．在牛顿三大定律中，牛顿第一定律给出了力的本质与惯性定律，是其他两条定律的前提和基础，故若一个参考系中物体的运动状态满足牛顿第一定律，其必然也满足第二与第三定律．据此，多数学者对其做出了相应的定义：在一定精度下，使牛顿第一定律成立的参考系叫惯性参考系；使牛顿第一定律不能成立的参考系叫非惯性参考系．因此从某种程度上说，牛顿第一定律定义了惯性系与非惯性系．

2 牛顿第二定律与参考系

牛顿第二定律是以牛顿第一定律为基础，对力与物体的运动状态变化的关系作的定量表述，其直接提供了物体所受合外力与其加速度之间的关系，通常表示为F=ma．我们知道，非惯性参考系与惯性参考系之间存在着相对的加速度，那么牛顿定律如何应用于非惯性系中？两参考系之间又有何关系呢？下面，基于牛顿第二定律来理解惯性参考系与非惯性参考系之间的关系以及非惯性系中各惯性力的物理意义．

2.1从“F=m(a相+a参)”与“F-ma参=ma相”两式出发理解惯性系与平动非惯性系

“F=ma”是牛顿第二定律最普遍的数学表达式．对于牛顿第二定律有以下解释：“F”为作用在质点或质点系上的合外力，“m”为质点或质点系的质量，“a”为质点或质点系运动的加速度．考虑到参考系的运动，绝对加速度可表示为：a=a相+a参，即F=ma=m(a相+a参)，其中“a相”为质点或质点系相对于参考系的加速度，“a参”为参考系的加速度．则等式“F=m(a相+a参)”的左边表示合外力，右边表示质点或质点系运动状态的变化．

现将等式“F=m(a相+a参)”变形为“F-ma参=ma相”，若还以上述“等式左边表示合外力，等式右边表示运动状态”的思想出发，可以发现其物理意义发生了巨大的变化．此时，等式左边“F-ma参”表示质点或质点系所受的合外力，而等式右边则表示其加速度为a相．

那么，这两个公式分别可适应用于哪些具体情境中呢？

现有两个参考系，地面参考系与动参考系，将地面参考系默认为惯性参考系，若动参考系相对于地面做直线加速运动，则为平动非惯性参考系．在惯性参考系中，牛顿第二定律适用，但在非惯性参考系中，牛顿第二定律就出现了问题．可以考虑一个简单情景：如图1所示，有一辆小车在地面上做匀加速直线运动，有一个质量为m的质点在小车内受到恒力作用做匀加速直线运动．

图1 质点运动示意图

定义水平向右为正方向，并令小车加速度为a参，则质点相对于小车的加速度为a相．以地面为参考系时，根据牛顿第二定律可列出方程：F=ma=m(a相+a参)．而以小车为参考物时，出现了矛盾：在小车中观察，质点的加速度为a相，根据牛顿第二定律得到方程：F=ma相，与上述方程“F=m(a相+a参)”产生矛盾，而导致这一矛盾的特殊所在是平动非惯性系相对惯性系具有加速度a参．为了解决这一矛盾，使牛顿第二定律在平动非惯性参考系中仍然适用，我们可以认为在非惯性系中的一切物体都受到某种大小为“-ma参”的力的作用，借以平衡此参考系相对于惯性参考系的加速度，此力称为惯性力F*，即F*=-ma参，其中“m”为非惯性系中被研究的质点或质点系的质量，“a参”为非惯性参考系相对惯性参考系的加速度，负号表示其方向与相对加速度方向相反．于是，在上述平动非惯性参考系中，质点的合外力为“F-ma参”，且其加速度为a相，从而满足等式“F-ma参=ma相”．

从“等式左边表示合外力，等式右边表示运动状态”的思想分析上述情景，可用等式“F=m(a相+a参)”来描述惯性系中质点的运动，引入惯性力后，用等式“F-ma参=ma相”来描述平动非惯性系中质点的运动．可见在具体情景下两式的物理含义大相径庭，但其归根结底都是牛顿第二定律的数学表达式．其实，转动非惯性系在引入一些惯性力后也可应用牛顿第二定律，下文将具体介绍．这样一来，在惯性参考系与非惯性参考系中皆可应用牛顿定律．所以说，惯性参考系与非惯性参考系是等价的．

2.2基于牛顿第二定律理解转动非惯性系中惯性离心力与科里奥利力的物理意义

根据参考系相对于惯性参考系的加速度的不同，非惯性参考系可以分为平动非惯性参考系和转动非惯性参考系两大类．上述情景就是简单的平动非惯性系，但由于地球本身的自转，其实际是一个转动非惯性系，所以地球上的物体更多需要利用转动系来解决问题．

在转动非惯性参考系中的物体也存在着惯性力，包括惯性离心力与科里奥利力．我们知道，平动非惯性系中惯性力的作用是平衡物体受到的恒力，那么同样是惯性力，在转动非惯性系中为什么又要引入惯性离心力与科里奥利力这两个力呢？它们分别具有什么物理意义呢？

图2 转动非惯性系中质点的运动

图3 惯性系中观察质点的运动轨迹

首先，在惯性系中建立x-y-z三维坐标，使x-y坐标系的原点为转盘圆心，则径向单位矢量的方向会随着圆盘转动的角度θ改变，得

er(t)=cosθ(t)ex+sinθ(t)ey

对时间求导，可得

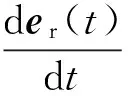
ωez×er(t)=ω×er(t)

图4 x-y平面解析图

由r=r(t)er(t)，对时间求导可得

下面，先对径向速度vr求导，可得径向加速度为

再对切向速度vt求导，可得切向加速度为

因此，总加速度为

ω×[ω×r(t)er(t)]

由此可以发现，质点相对于惯性系的加速度共由五部分组成，则其实际所受到的合力也一定可分为这五部分，根据牛顿第二定律求得质点受到的合外力为

mω×[ω×r(t)er(t)]

mω×[ω×r(t)er(t)]

3 牛顿第三定律与参考系

通过引入惯性力，牛顿第一定律和第二定律能够从惯性参考系推广到非惯性参考系，那么牛顿第三定律也是如此吗？

我们知道，牛顿第三定律揭示了作用力与反作用力之间的关系．当我们谈及作用力时，总是有施力物体与受力物体，但惯性力是我们在出现矛盾时假想出来的力，并非真实存在的，因此它并没有真正的施力物体．而物体之间的作用又是相互的，没有施力物体也即没有受力物体，所以惯性力不存在反作用力，它不属于相互作用力的范畴．因此，我们在讨论牛顿第三定律的适用性时不需要考虑惯性力．

在验证牛顿第三定律的实验中，通常选用两个力传感器进行互拉，我们会发现无论这两个力传感器是静止的、匀速运动的还是变速运动的，它们在计算机上显示的示数总是相等．若以地面为惯性参考系，那么静止和匀速运动时的力传感器都属于惯性系；而当力传感器变速运动时，它们自身就属于非惯性参考系．此时相等的示数说明：在不附加其他条件的情况下，牛顿第三定律在非惯性系中仍然适用．因此，牛顿第三定律在惯性系与非惯性系中都适用．也即是说，牛顿第三定律与参考系的选取并没有必然的联系．

4 总结

从定性的角度而言，牛顿第一定律定义了惯性系与非惯性系；从定量的角度来说，从牛顿第二定律的定量表达式出发引入了惯性力，以此平衡在非惯性系中物体受到的真实力，使牛顿第一与第二定律在非惯性系中仍然适用；对于牛顿第三定律，描述的是相互作用力之间的关系，不需要考虑不属于相互作用的惯性力，因此牛顿第三定律与参考系的选取无关．

1 冯杰.大学物理专题研究.北京:北京大学出版社,2011.95～108

2 漆安慎,杜婵英.力学(第二版).北京:高等教育出版社,2005.85～91

3 周衍柏. 理论力学.北京:高等教育出版社,1997.180～186

TalkingabouttheNewton′sLawandtheReferenceSystem

Hu Min Guo Changjiang Gu Feng

(Mathematics & Science College of Shanghai Narmal University,Shanghai 200234)

This paper briefly sorts out the relationship between Newton′s law and the reference system. Firstly,Newton′s first law is used to analyze the essential difference between the inertial reference system and the non-inertial reference system. Then, based on the understanding of Newton′s second law, the relationship between the inertial reference system and the translational non-inertial reference system is analyzed from the distinction and contact between ′F=m(a相+a参)′and ′F-ma参=ma相′.And the physical meaning of the inertial forces in the rotatingnon-inertial reference system is explained. Finally, it is pointed out that Newton's third law has nothing to do with the selection of the reference system.

Newton′s law;inertial reference system;non-inertial reference system;inertial forces

作者介绍：胡敏(1994- )，女，在读硕士研究生.

指导教师：郭长江(1974- )，男，中教高级，主要从事中学物理课程与教学研究.

2017-03-13)