对匀强磁场中球面摆运动规律的研究

姜付锦

(武汉市黄陂区第一中学 湖北 武汉 430300)

郎 军

(重庆市第十一中学校 重庆 400061)

对匀强磁场中球面摆运动规律的研究

姜付锦

(武汉市黄陂区第一中学 湖北 武汉 430300)

郎 军

(重庆市第十一中学校 重庆 400061)

通过对匀强磁场中一种球面摆运动的理论研究，证明了其正则角动量守恒，分析了当小球的速率有微扰时运动的定量规律以及不脱离而稳定运动的条件，最后通过数值模拟直观地显示了运动轨迹并验证了理论分析的结果．

球面摆 微扰 正则角动量 数值模拟

1 提出问题

如图1所示，半径为R的光滑球面固定在空间某点，磁感应强度为B的匀强磁场竖直向下穿过球面．一个质量为m，带电荷量为+q的小球正在某一个水平面上做匀速圆周运动，已知小球与球心连线与竖直方向上的夹角为θ0，若小球的速度突然有一个变化量±Δv(方向不变)时，试分析以后小球的运动规律．

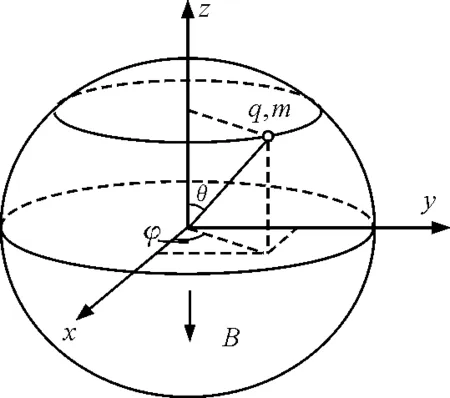
图1 提出问题

2 理论研究

2.1理论依据

2.1.1 动力学方程

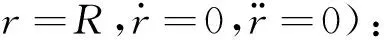
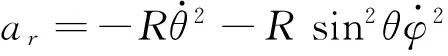
两个方向上的分速度为

在er方向：

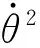
化简得

FN=mgcosθ+qBvφsinθ-

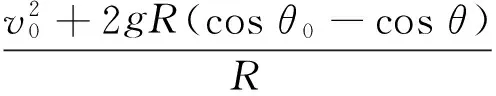
(1)

在eθ方向：

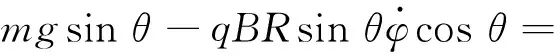
eφ方向：

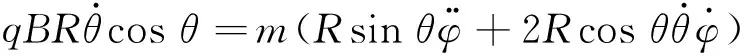
由以上两式求得

2.1.2 正则角动量守恒和机械能守恒

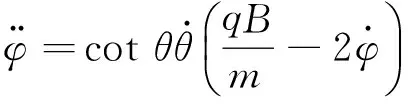
变为

等式两边同时乘于sinθ，并对时间不定积分得

即

(2)

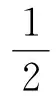
将小球的运动分解为经线运动和纬线运动，由机械能守恒和正则角动量守恒有

经线

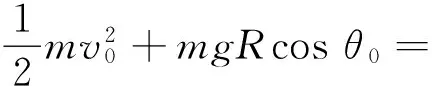
纬线

联立以上两式求得

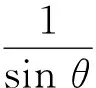
(3)

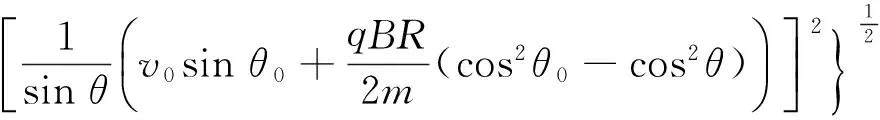
(4)

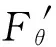
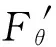
(5)

2.2运动规律

2.2.1 做稳定圆周运动的初速度条件

设初速度为v0,要做稳定圆周运动，则

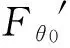
由式(5)得

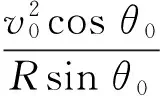
化简得

求得

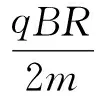
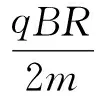
2.2.2 变轨运动规律

以下讨论中，设+q被双向约束在球面上(如设想有一根轻杆与+q相连，轻杆可绕球心各向自由转动)，如图2所示.

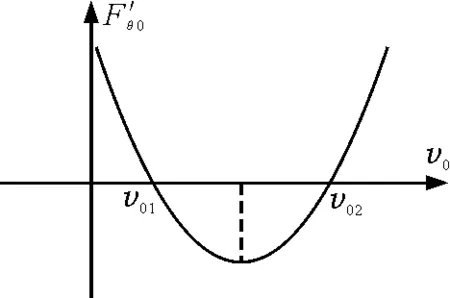
图2 极角合力与初速度关系

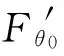
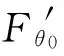
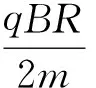
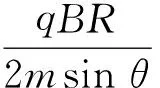
(6)

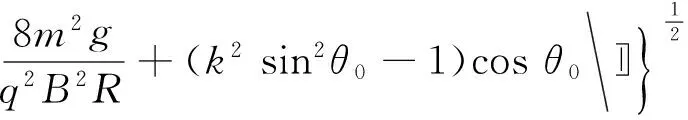
(7)

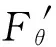
(8)

FN=3mgλ-2mgcosθ0+

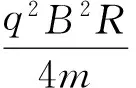
(9)

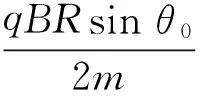
(2)最高点(或最低点)的极角θm

在最高点(或最低点)：vθ=0，由式(7)得

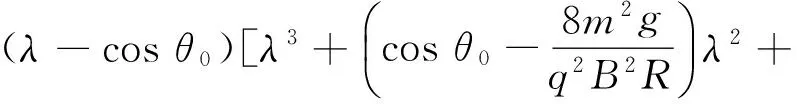
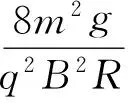
得

λ1=cosθ0

和

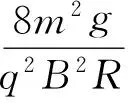
令

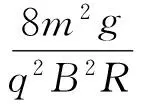
由一元三次方程的卡尔丹公式可得

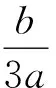
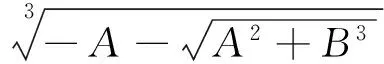
(10)

式中

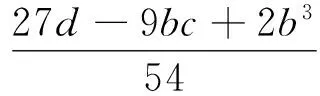
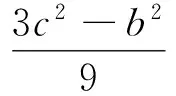
而λ3,λ4为复数根(舍去)，所以

θm=arccosλ2

讨论：

(1)若k=0，式(7)变为

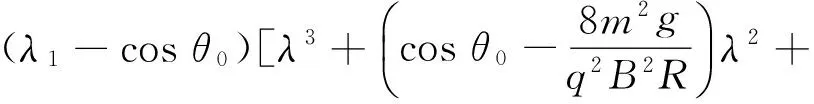
(k2sin2θ0-1)cosθ0]=0

进一步化简为

(λ1-cosθ0)(λ-1)(λ+1)

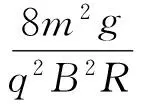
这里λ1=cosθ0为初态值，λ2为最高点值，λ3,λ4舍去．

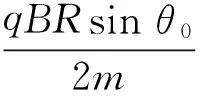
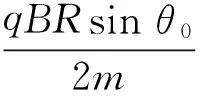
(3)沿经线方向的运动周期Tθ

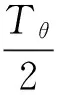
(11)

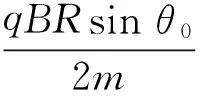
在一个周期内，沿纬线方向转过的角度Δφ.

由于

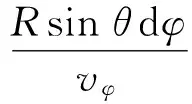
所以

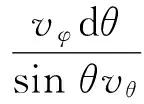
轨迹闭合性的条件：n1Δφ=n22π(n1,n2为正整数)．

2.2.3 不脱离的条件

(1)如果|k|值太大，初始状态可能就会脱离球面，由θ=θ0时，FN≥0求出k0.

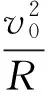
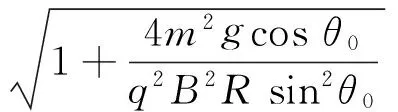
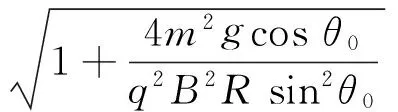
(12)

(2)如果|k|值太小，在向上变轨的过程中会出现脱轨，要求运动轨迹的最高点不脱离球面，由FN(θ)≥0,vθ(θ)=0可求得k1.

利用式(9)，由FN(θ)=0求得

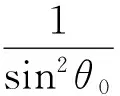
(13)

由vθ=0及式(7)和式(13)化简得到一个关于λ的一元三次方程

λ3+bλ2+cλ+d=0

式中

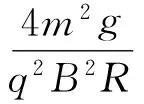
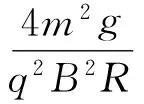
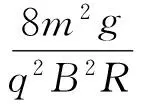
由卡尔丹公式[参见式(10)]可得求得λ.

由求得的λ代入式(13)可求得k绝对值，设为k1．

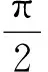
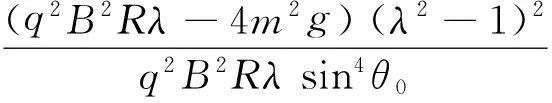
(14)

将k2的值代入vθ=0，利用式(7)，化简有

因此λ1=λ2=cosθ0(这为初态值，不是我们要求的情况，舍去)

于是得到

由卡尔丹公式求得λ3的值(另两解为复数解，舍去．)

将λ3的值代入式(14)求得k2的值．

(4)不脱离的条件为：k1≤|k|≤min(k0,k2)，若k1无解，则|k|≤min(k0,k2)

(5)实例分析

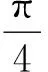
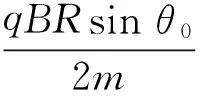
因此不脱离的条件为：0.784<|k|<1.068

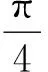
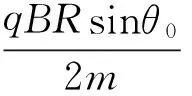
因此不脱离的条件为：|k|<0.713.

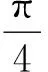
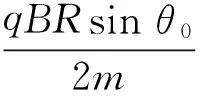
因此不脱离的条件为：0.905<|k|<1.031.

2.3特例分析

2.3.1 当v0=0时

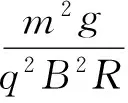
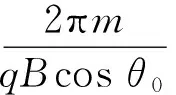
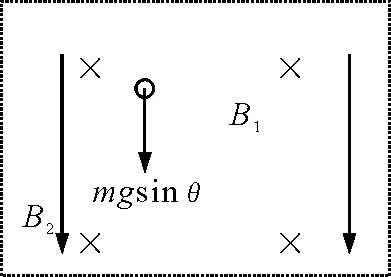
图3 小球在近似平面上的运动

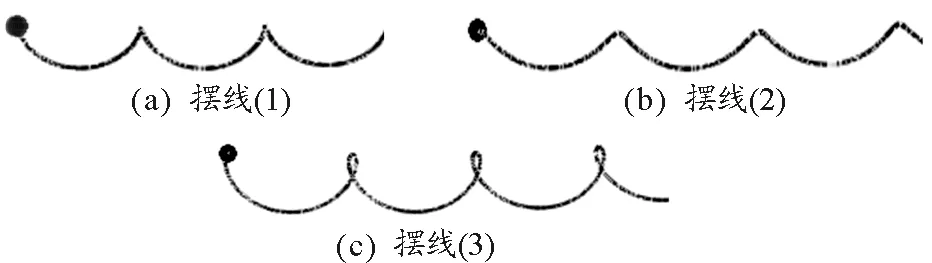
图4

2.3.2v0=v01±Δv或v0=v02±Δv,Δv≪v01或Δv≪v02

(1)在这种微扰下，小球在经线方向极角的变化非常小，在经线方向近似做简谐运动.

(2)振动周期的计算

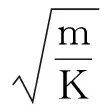
式中

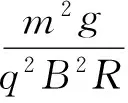
v02±Δv与v0=v01∓Δv两种情况的Tθ相同，结合特例1可知两种情况下均有

3 数值模拟

在Mathcad中输入有关微分方程及初始条件，设置好q，m，g，B，v0等有关参数后，可以得到不同条件下小球运动规律的数值模拟结果．

3.1实例1的数值模拟

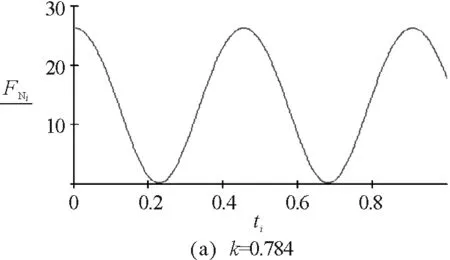
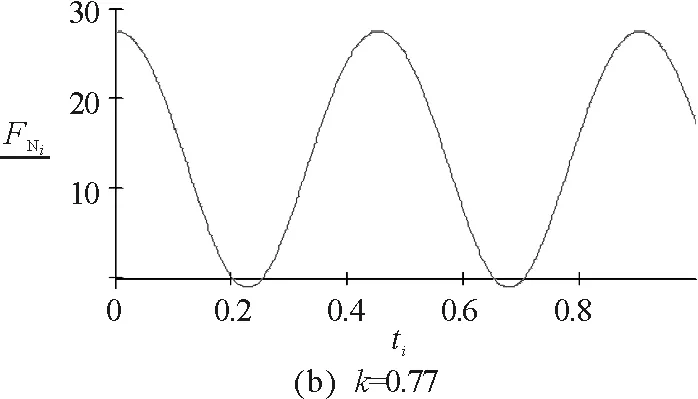
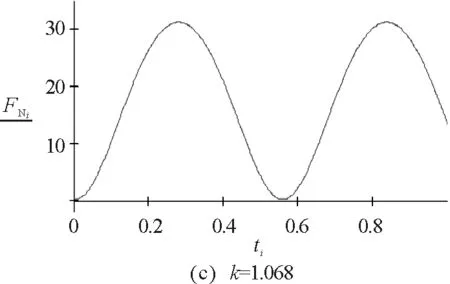
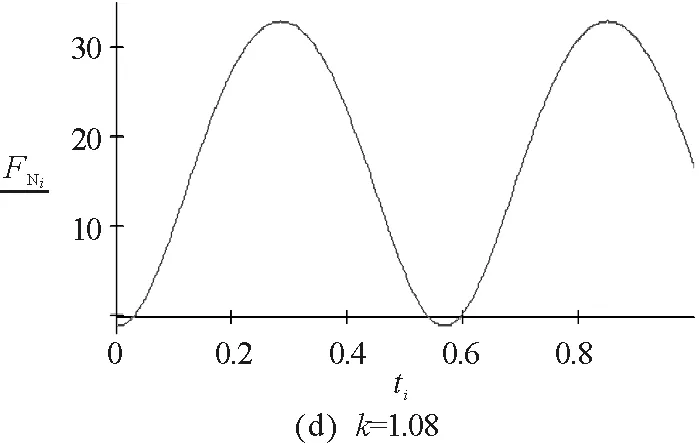
图5 实例1的数值模拟

3.2实例2的数值模拟

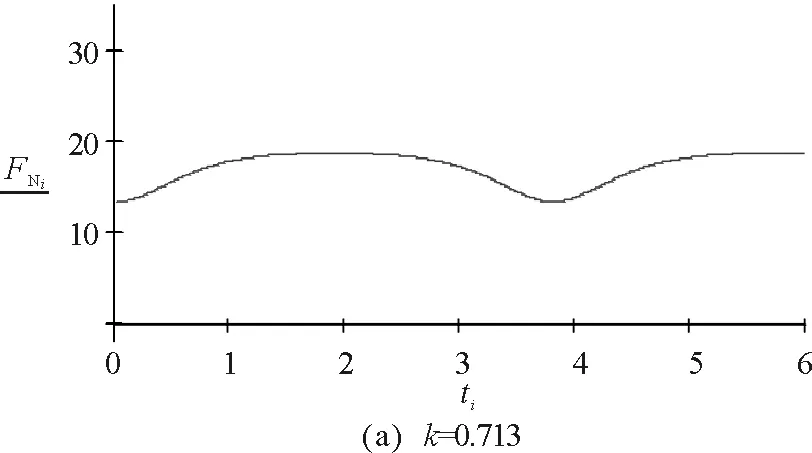
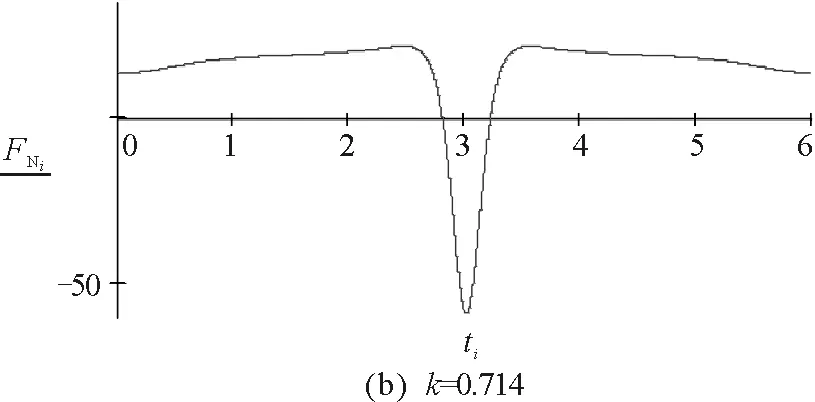
图6 实例2的数值模拟

3.3实例3的数值模拟

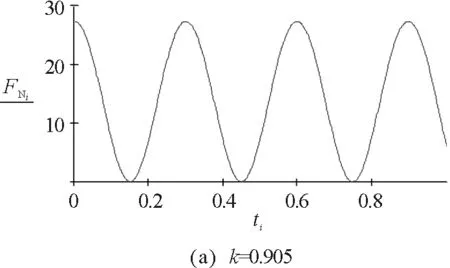
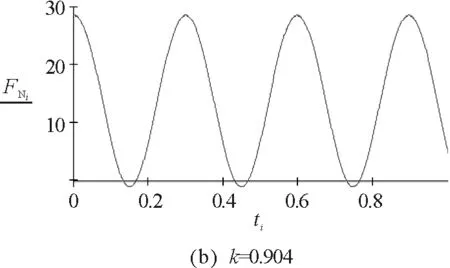
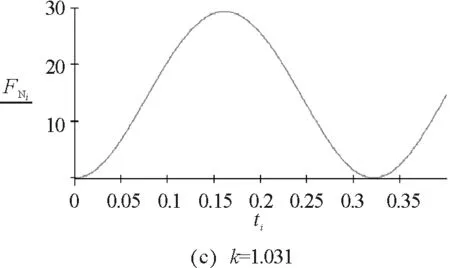
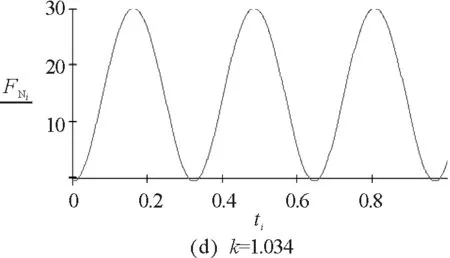
图7 实例3的数值模拟

3.4小球运动轨迹的数值模拟

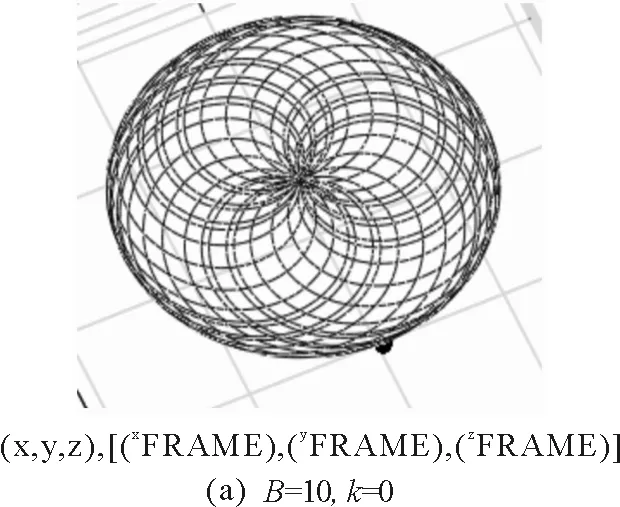
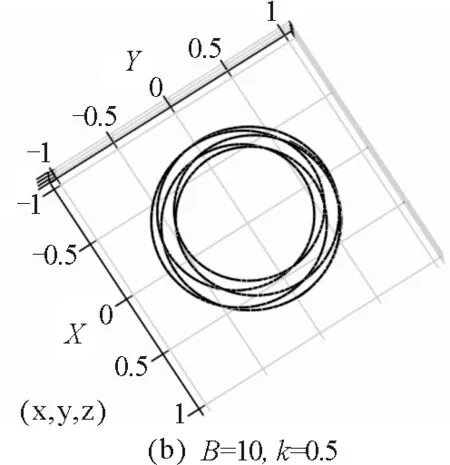
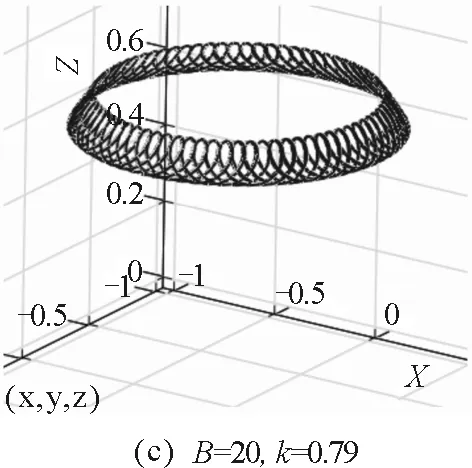
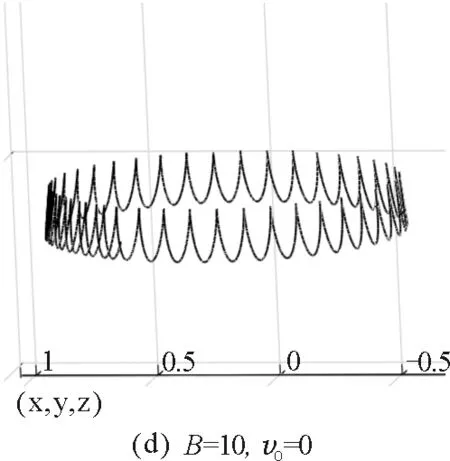
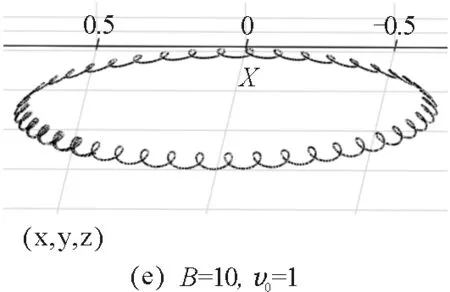
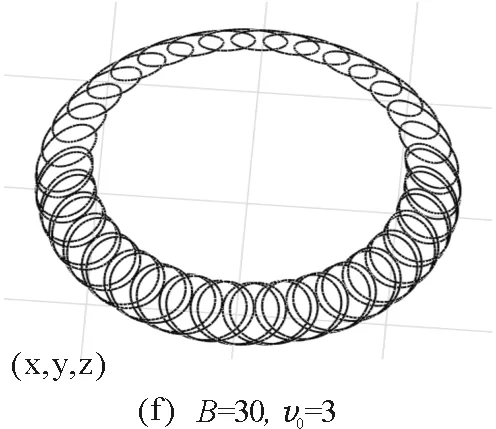
图10 小球在不同初始值时运动轨迹的数值模拟

4 结束语

1 何广源，黄迺本.球面摆的运动方程数值模拟和实验验证．大学物理，2006，25(7)：46～49

2 赵凯华.磁场中正则动量守恒定律的应用．大学物理，1988，1(3)：9

3 涂德新.复合场中的守恒量．物理通报，2016(4)：69～71

2017-04-24)