自行车稳定性问题的研究与诠释
2017-11-16黄绍书
黄绍书
(六盘水市第23中学 贵州 六盘水 553000)
蒋金团
(施甸县第一中学 云南 保山 678200)
自行车稳定性问题的研究与诠释
黄绍书
(六盘水市第23中学 贵州 六盘水 553000)
蒋金团
(施甸县第一中学 云南 保山 678200)
根据刚体转动的力矩平衡,从转动相对定点悬空的角度,给出自行车“转弯不倒”的约束关系,并由此剖析自行车在微小扰动情况下,能够自动恢复稳定的原因.最后,结合自行车转弯过程中的转动惯量及回转半径,给出自行车在“转弯不倒”条件下的最大角速度解析式.
自行车稳定性 转弯不倒 陀螺效应 力矩平衡 诠释
1 引言
自行车是最普及的大众简易交通工具,它的发明已有200多年.而对自行车稳定性问题的研究和讨论,同样具有悠久的历史.这方面已发表的科普文章近百篇,通过检索查阅近40年来的部分文献资料[1~4],发现它们基本都是从动力学微分方程入手分析,而未离开流行上百年的离心力效应和陀螺效应的观点.
关于自行车稳定性问题的研究和讨论,从未停止,并曾几度掀起热潮.1970年,英国一位化学家Jones对传统的陀螺效应产生怀疑[5].于是,他设计一辆无陀螺效应的自行车,就是在普通自行车的前轮上并排安装一个同样大小但不接触地面的轮子,这一轮子与正常车轮反向转动时,即可消除陀螺效应.Jones的这一实践表明,消除陀螺效应后的高速运动的自行车同样能够维持稳定.也就是说,陀螺效应对自行车的稳定性没有明显的影响.
2012年1月,美国科普杂志Discover Magazine评选了2011年全球100个顶尖科学故事.其中“自行车的新物理”荣居第26位.为此,其困扰公众的自行车稳定性问题再度热议起来[6].
至如今,自行车稳定性问题仍然是一个悬而未决的科学悬案.本文试图从转动相对定点悬空的角度,分析给出自行车“转弯不倒”的约束关系,并由此对自行车在微小扰动情况下,能够自动恢复稳定的原因进行剖析.
2 从自行车“转弯不倒”谈起
骑着自行车转弯时,人和车都总是向弯道的内侧倾斜.因此,人和车组成的系统(以下简称人车系统)的重力作用线不在支撑面上,那么,为什么人车系统不会倾倒呢?
2.1自行车转弯的一般认识
如图1所示,骑着自行车在水平弯道转弯时的情形.
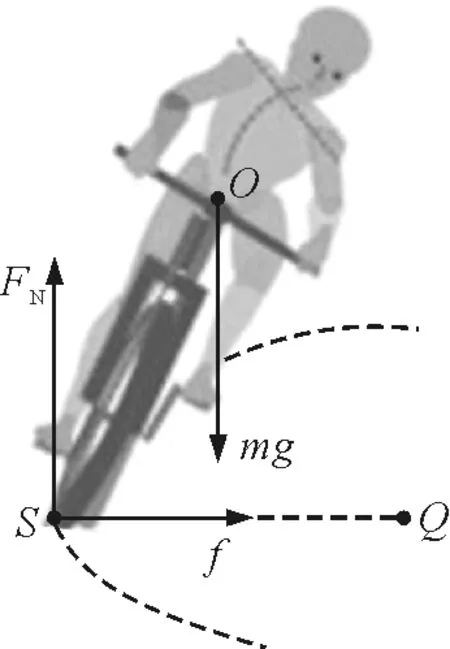
图1 人骑自行车受力分析
为了减少计算的复杂性,这里将人车系统受到力简化为3个,即人车系统的重力mg,路面对车轮的支持力FN及法向摩擦力f.设人车系统做圆周运动的角速度为ω,质心轨道半径为r.那么,在竖直方向
FN-mg=0
(1)
即FN与mg等大反向,合力为零.
在水平方向
f=mrω2
(2)
即摩擦力f提供转弯所需的向心力.
显然,这一分析过程中,没有考虑人车系统的空间尺度,也没有考虑支持力FN与重力mg之间是非共点力的关系,仅将人车系统的转动考虑成质点的圆周运动.因此,这一分析不能解释“转弯不倒”的问题.
2.2自行车“转弯不倒”约束条件
事实上,人车系统是一个相对定轴转动系统.那么,什么力的力矩与重力力矩平衡,使得人车系统“转弯不倒”,而维系着动态平衡状态呢?这就是公众不能释疑的根本性困扰.
为了便于讨论,将人车系统简化成刚体.人车系统转弯时,实际是绕某一竖直轴转动,其转动面为一圆锥面,如图2所示.受力情况与图1一致,不再赘述.设人车系统的重心为O,转动过程中的倾斜角为θ,转动相对定点为P,转动轴为过P点的竖直轴,路面支撑动点S与O,P之间的距离分别为l和L.那么,重力mg,支持力FN和摩擦力f对P点的力矩分别为
MG=mg(L-l)cosθ
(3)
MF=FNLcosθ
(4)
Mf=fLsinθ
(5)
由图2可知,支持力FN与重力mg的大小是相等的.在人车系统逐渐倾斜过程中,主动力矩MG和MF将随倾斜角θ的减小而增大,而被动力矩Mf的变化比较复杂,因为摩檫力f的大小与其力臂存在相反的变化趋势.人车系统“倒”与“不倒”,完全决定于这3个力矩之间的约束关系,亦就是
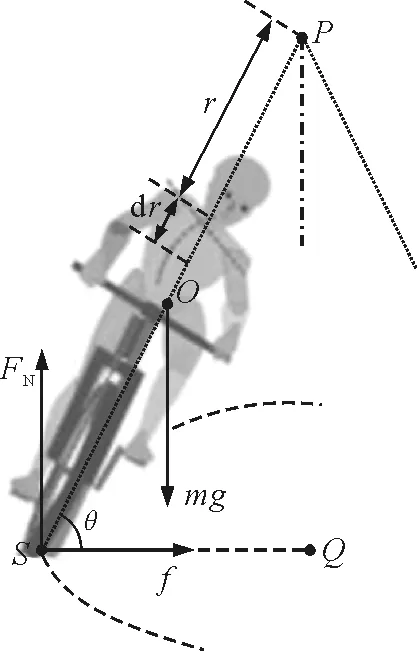
图2 力矩之间的约束关系
(1)当Mf>MF-MG,即

时,倾斜角θ将增大而“不倒”,且这与人为控制没有多大的关系.
(2)当Mf=MF-MG,即

时,倾斜角θ将不变而“不倒”.
(3)当Mf 时,倾斜角θ将减小.若此时的摩擦力已达到最大静摩擦力fm,则人车系统即刻“倒”;若此时的摩擦力未达到最大静摩擦力fm,则人车系统随着θ减小到一定值时仍然“倒”. 在人车系统转弯的角速度没有超过最大角速度之前,摩擦力的大小就处在零与最大静摩擦力fm之间的变化,且摩擦力的大小由人车系统的转动角速度、转动半径及倾斜角确定,见式(8)~(13)的推导.这时,摩擦力矩Mf也随之变化. 自行车的稳定性是指正常沿直线自由高速行驶的自行车,在某种扰动情况下,其运动轨迹偏离直线后会自动(非人为控制)恢复直线稳定运动的现象. 自行车高速行驶条件下,在受到某种扰动时,由于前叉(龙头)的灵活转动,就会由直线运动变为圆弧运动.这时,车身向内倾斜,而车身“倒”与“不倒”符合图2所示模型的上述讨论. 高速行驶的自行车在受到微小扰动的情况下,转动相对定点P的空间位置较高,车身的倾斜角θ较大,路面对车轮的法向摩擦力f的力臂较长,车身的重力mg和路面对车轮的支持力FN的力臂较短.根据图2所示模型的讨论可知,这时,这3个力对转动相对定点P的力矩之间往往满足 Mf>MF-MG 即 (6) 因此,这种情况下,车身的倾斜角θ会逐渐增大.这样,就维持了自行车的稳定性.从式(2)可以看出,这时自行车的速度越大,其离心运动(向外侧滑)的趋势就越明显,路面对车轮的法向摩擦力f就越大,自行车越容易自动恢复稳定运动状态. 当自行车受到扰动比较剧烈时,转动相对定点P的空间位置过度偏低,车身的倾斜角θ较小,路面对车轮的法向摩擦力f的力臂较短,车身的重力mg和路面对车轮的支持力FN的力臂较长.这时,这3个力对转动相对定点P的力矩之间通常满足 Mf 即 (7) 因此,这种情况下,车身的倾斜角θ会越来越小,自行车的稳定性将不能继续维持. 这里还需特别说明,陀螺效应对于自行车的维持稳定确实有一定的作用.但是,由于自行车的车轮转动角速度一般远远不及高速旋转的陀螺角速度大,因此,陀螺效应对自行车的维持稳定的作用并不明显.另外,自行车前叉(龙头)的灵活转动且呈倾斜状的结构,对于自行车自动恢复稳定起着至关重要的作用. 人车系统转弯的最大角速度ωm与人车系统对转动定点(相对)P的转动惯量J或回转半径r0[6]有关,同时还与人车系统的最小倾斜角θn有关. 再次将人车系统进一步看成质量均匀分布的细柱型刚体.根据前面设定,人车系统的竖直面总长度应为2l.令人车系统的线密度为λ.在距离图2中的P点为r处,取一长度元dr,则长度元的质量为dm=λdr.因此,人车系统对转动定点(相对)P的转动惯量为 (8) 回转半径为 (9) 若设车轮与路面之间的最大静摩擦因数为μm,那么,由图2可知,人车系统转弯的最小倾斜角θn满足 (10) 由于地面对车轮的支持力FN等于人车系统的重力mg,因此人车系统转弯过程中受到路面的最大静摩擦力fm为 fm=μmmg (11) 这一最大静摩擦力就是人车系统转弯时的最大向心力.刚体绕定轴转动时,由于转动惯量的影响,向心力应等效作用于刚体的微分质量集中点.因此,人车系统转弯过程中,最大角速度ωm满足 fm=mr0ωm2cosθn (12) 代入各量代数式,化简可得 (13) (1)人车系统在转弯过程中,由于路面的平整度或人为因素,会使其受到随机扰动,从而使图2中的转动相对定点P以及过该点的竖直轴具有瞬时性,具体可由人车系统的动力学微分方程瞬时关系确定.因此,各式中涉及的路面支撑点S与转动定点P之间的距离L以及转动惯量J,回转半径r0,最大角速度ωm等也都具有瞬时性. (2)根据(6)、(7)两式的分析表明,本文的研究诠释了自行车能够自动恢复稳定的根本原因,解决了自行车稳定性这一悬而未决的问题. 1 马中兴.自行车的动力学方程及运动稳定性.陕西科学技术大学学报,1982(10):91~105 2 魏德明.论自行车的稳定性.昆明工学院学报,1986(2):117~122 3 徐华峰.自行车运动稳定性研究.振动与冲击,1994(3):70~75 4 林修成,张朝阳.自行车行驶稳定性及后进动性的力学分析.合肥工业大学学报,2011(4):287~291 5 刘延柱. 关于自行车的稳定性. 力学与实践, 2012(2): 90~93 6 哈尔滨工业大学理论力学教研室.理论力学(Ⅰ).北京.高等教育出版社.2009.259~272 ResearchandInterpretationonBicycleStabilityIssue Huang Shaoshu (Liu Panshui No.23 Middle School,Liu Panshui,GuiZhou 553000) Jiang Jintuan (ShiDian No.1 Middle School,BaoShan,YunNan 678200) According to the rigid body rotation moment balance,from the Angle of rotation relative fixed-point dangling give bicycle turn "fail" constraints,and analyze the bike under the condition of small disturbance,automatically restore stability.Finally,the maximum angular velocity resolution of the bicycle in the condition of "turn down" is given by the rotational inertia and the radius of rotation. bicycle stability;turning to fail;centrifugal effect;the gyroscopic effect;conical surface;torque balance;interpretation 2017-05-25)
3 自行车稳定性的剖析

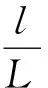

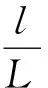
4 最大角速度





5 说明与结论
