超复数Fourier变换耦合位置扰乱的彩色图像哈希算法*

冯 贺，常国权，郭晓波

安阳工学院 计算机科学与信息工程学院，河南 安阳 455000

超复数Fourier变换耦合位置扰乱的彩色图像哈希算法*

冯 贺+，常国权，郭晓波

安阳工学院 计算机科学与信息工程学院，河南 安阳 455000

当前图像哈希算法大都是通过将彩图三分量R、G、B转换成灰度图像来生成哈希，丢失了色度信息，降低了算法对篡改内容的检测精度与敏感性的不足，为了解决上述问题，提出了超复数离散傅里叶变换耦合位置随机扰乱的彩色图像哈希认证算法。首先，通过构建新的扩散系数，从而改进偏微分模型PED(partial differential equation)，对输入图像进行预处理，增强算法对图像缩放的鲁棒性，从而最小化图像信息丢失对算法的影响；再引入对数极坐标变换机制，将预处理图像变成二次图像；基于超复数理论与Fourier变换，将彩图三分量R、G、B视为四元数的虚部，建立四元离散Fourier变换机制，提取抗旋转篡改的图像特征；并基于Logistic混沌映射，设计位置扰乱机制，对四元离散Fourier变换低频幅度系数进行随机置乱；根据置乱后的幅度系数，构建图像哈希模型；最后，引入汉明距离，优化认证阈值，建立图像哈希相似度计算模型，以评估初始图像与用户接收图像的哈希相似度，完成图像内容的真伪认证。实验结果显示：与当前图像哈希算法相比，在处理彩色图像时，该算法具有更强的鲁棒性与安全性，呈现出更好的ROC曲线特性，能够有效识别亮度、旋转、噪声以及缩放等篡改攻击。

图像哈希；超复数Fourier变换；对数极坐标变换；位置扰乱机制；真伪认证；汉明距离

1 引言

随着计算机技术的快速发展，图像因其含有众多信息，已成为当前人们日常信息交流中最为直观的载体，给人们的生活带来了极大的方便[1]。与此同时，各种图像编辑软件也得到了迅猛发展，图像内容很容易被这些软件修改，且不留痕迹或留下很少伪造痕迹，给图像真伪识别以及用户安全带来巨大麻烦，信息安全已成为当前各国的关注焦点[2]。为此，当前学者与研究人员设计了相应的图像认证技术，而图像哈希是图像内容真伪检测常用的技术之一，其性能的优异直接影响了伪造检测精度[3]。图像哈希又称图像摘要或图像标识码，从短的二进制或实数序列来提取图像重要特征，是一种基于图像视觉内容的压缩表达，在图像匹配、图像检索以及图像伪造检测领域被广泛采用[4]。在实际应用中，哈希函数可作为图像的惟一表示而用于其信息的真伪决策，即使图像内容发生微小变化，其哈希值都会产生巨大变换[4]。哈希的这种特性，能够较好地用于图像信息安全检测领域。

近年来，图像哈希算法已被诸多学者研究，取得了较好的进展。一般而言，图像哈希算法主要分为3个步骤：图像预处理、图像特征提取以及哈希模型建立。其中图像特征提取是整个算法的核心，对图像真伪认证有着重要影响。当前，图像哈希算法的特征提取技术主要分为以下类型：基于离散余弦变换、离散小波变换、矩阵分解、傅里叶变换以及Zernike矩。如曾勇等人[5]提出了基于离散余弦变换的感知哈希算法，通过对输入图像进行归一化预处理，使得算法具有几何不变性，然后利用离散余弦变换进行图像特征系数的提取，并用混沌序列发生器加密图像，从而生成哈希序列，实验结果显示其哈希算法具有较好的鲁棒性。Tang等人[6]设计了局部熵耦合小波变换的图哈希重构算法，通过利用像素块的熵值来描述图像纹理，再利用小波变换处理图像块的熵值，实现特征压缩与哈希重构，实验结果显示该算法具有较好的抗旋转变换能力。Tang等人[7]提出了环形分割与非负矩阵分解的图像哈希生成算法，通过构建旋转不变的二次图像结构来增强算法鲁棒性，通过内容保持操作因子，使得非负矩阵分解呈现近线性变化，从而准确测量哈希相似度，实验结果显示该算法具有良好的鲁棒性，呈现出较好的ROC曲线特性。Qin等人[8]为了提高哈希算法的安全性，提出了基于离散傅里叶变换的图像哈希算法，通过对输入图像完成预处理，提高算法的尺度缩放不变性，联合旋转投影机制与离散傅里叶变换，提取二次图像的频域特征，通过置乱函数，扰乱特征矢量，再对其进行量化，获取二值哈希序列，实验结果显示该算法具有较高的敏感性与安全性。Zhao等人[9]为了提高图像伪造内容的检测精度，设计了基于Zernike矩与局部特征的图像哈希算法，利用Zernike矩提取图像全局特征与显著区域的局部特征，来描述图像纹理与位置特征，通过全局与局部联合特征，利用汉明距离来完成图像内容认证，实验结果验证了该算法的优异性。

但是，当前图像哈希算法在处理彩色图像时，主要是将彩图的3个频道（R、G、B）转换成灰度图像，通过提取其灰度特征来获取哈希序列，从而丢失了彩图的色度信息，使得算法的鲁棒性与认证能力不佳。

为此，本文提出了超复数离散傅里叶变换耦合位置扰乱的彩色图像哈希认证算法。首先，改进PED模型，对输入图像进行预处理，增强算法对图像缩放的鲁棒性，从而最小化图像信息丢失对算法的影响，尤其是图像角点处的像素信息的丢失；利用对数极坐标变换机制，将预处理图像变成二次图像；基于超复数理论与Fourier变换，建立四元离散Fourier变换机制，在保留图像色度信息的同时，同步处理彩图三通道R、G、B，提取抗旋转篡改的图像特征；并设计位置扰乱机制，对四元离散Fourier变换低频幅度系数进行加密；再根据置乱后的低频幅度系数，构建图像哈希模型，增强哈希模型的安全性；利用加密哈希模型，引入汉明距离，计算初始图像与用户接收图像的哈希值的相似度，完成图像内容的真伪认证。最后，测试本文哈希算法的鲁棒性与对伪造图像的检测精度。

2 本文图像哈希算法

本文图像哈希算法过程见图1，其主要步骤为：（1）基于改进的PED（partial differential equation）模型与重缩放的图像预处理；（2）利用对数极坐标变换与多元离散Fourier机制的鲁棒图像低频幅度系数提取；（3）图像哈希生成与认证。通过对图像进行重缩放与PED模型平滑处理，使得生成的哈希序列具有固定的长度，增强算法对图像缩放的鲁棒性，从而最小化图像信息丢失对算法的影响。引入对数极坐标变换对预处理图像进行转变，再建立四元离散Fourier变换机制，同步处理彩图三通道R、G、B，提取抗旋转的图像特征；为了增强哈希序列的安全性，设计位置扰乱机制，对低频幅度系数进行随机置乱；再利用置乱后的四元离散Fourier变换的低频系数，构建图像哈希序列，并联合汉明距离，完成图像内容的真伪认证。

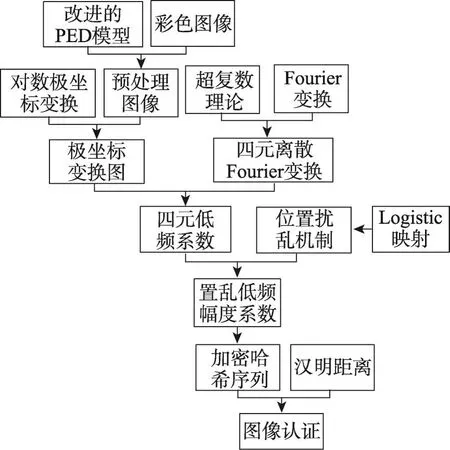
Fig.1 Image Hash authentication algorithm process in this paper图1 本文图像哈希认证算法过程

2.1 图像预处理

本文图像预处理机制见图2。假设彩色图像I0尺寸为M×N，首先对其重缩放，固定其尺寸为M×M，从而确保不同大小的图像哈希具有一个固定的长度，增强图像对缩放篡改手段的鲁棒性，本文取M=256。随后，为了增加图像哈希算法的敏感性，本文基于经典的PED模型[10]，通过构建新的扩散系数，对其进行了改进：

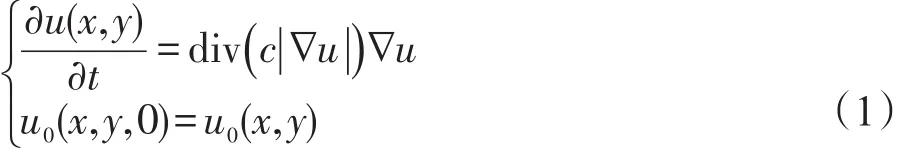
其中，u(x,y)代表初始图像；c(x)代表扩散系数，其；t为时间变量；u(x,y,t)代表平滑处理后的图像；∇u是图像梯度模；u0(x,y)是初始图像。

由于式（1）中的扩散系数是病态的，在反复迭代中，会导致图像重要边缘模糊[10]。为此，本文规定当x＞σ时，强制c(x)=0，从而构建了新的扩散系数：

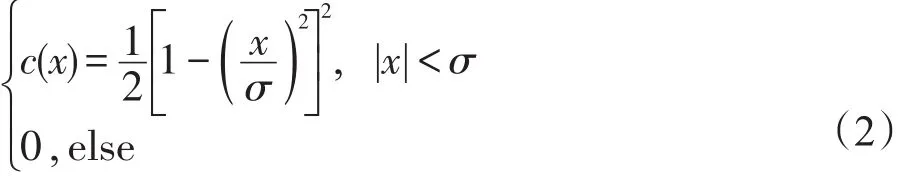
其中，σ代表尺度因子。

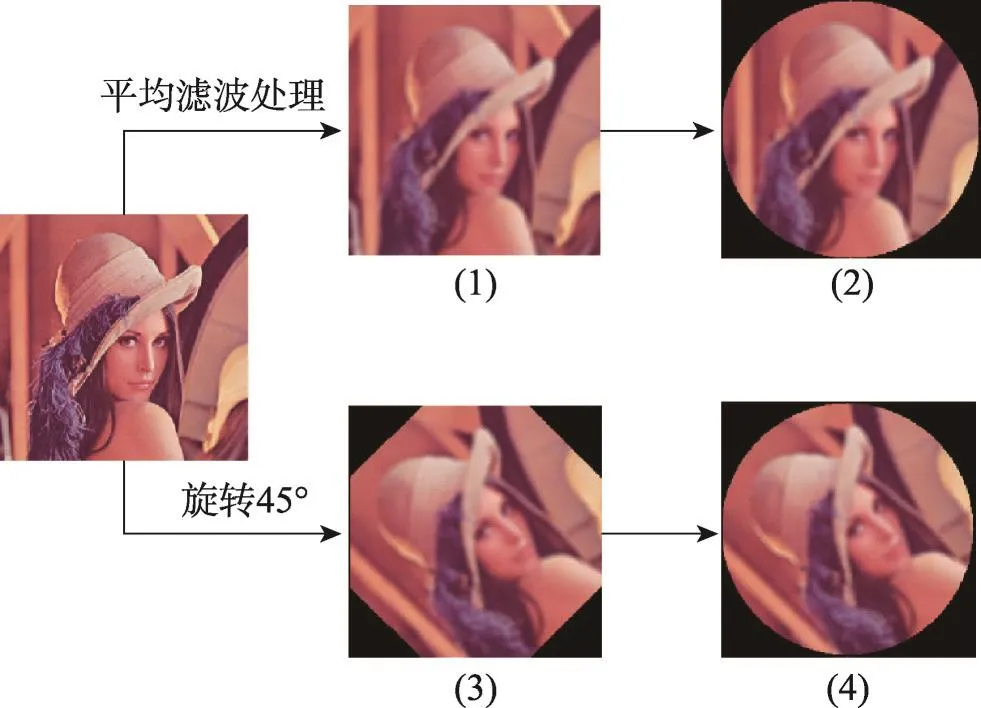
Fig.2 Image preprocessing mechanism in this paper图2 本文图像预处理机制

将式（2）代入式（1）中，得到了改进的PED模型，在不损害图像内容的前提下，保持图像的重要信息，剔除噪声与无关紧要的细节，见图2（2）。考虑到图像可以被旋转，本文只考虑图像内切圆中的平滑像素，见图2（4），且旋转前后图像具有相同的像素值。通过本文预处理机制，在面对大角度旋转时，能够最小化图像信息丢失对算法的影响，尤其是图像角点处的信息丢失。

2.2 图像特征提取

2.2.1 对数极坐标变换

通过图像预处理后，使得算法对图像缩放具有较强的鲁棒性。随后，本文通过引入对数极坐标变换[11]，并建立多元离散Fourier变换机制，提取预处理图像的抗旋转特征。首先，通过对数极坐标变换[11]，将预处理图像变成二次图像。假设f1(x,y)是旋转后的预处理图像，角度为θ，则旋转彩色图像f1(x,y)为：

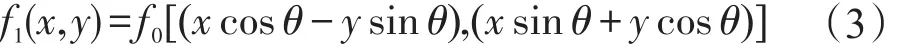
其中，f0代表预处理彩图；θ为旋转角度；cos、sin分别是余弦、正弦函数。

由于对数极坐标变换具有较强的抗旋转与缩放性[12]，即卡迪尔空间内的旋转与缩放篡改可视为对数极坐标变换机制中的水平、垂直两方向上的平移操作，见图3。故本文利用该机制将图像转换成对数极坐标域。若(x,y)为图像卡迪尔空间内的像素点；ρ是对数极坐标变换机制的极径，而θ是幅角，则图像的对数极坐标为：

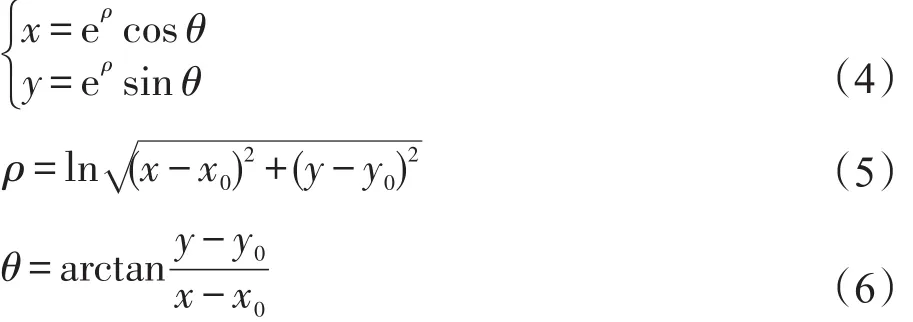
其中，(x0,y0)代表图像中心点；ρ是对数极坐标变换机制的极径，而θ是幅角；e为指数函数。

再将式（4）～（6）代入式（3）中，旋转图像的对数极坐标域为：

其中，f1(ρ,θ)是旋转彩色图像f1(x,y)的对数极坐标变换结果；f0(ρ,θ)是初始彩图f0(x,y)对应的对数极坐标变换结果。

依据式（9）可知，图像经旋转篡改后，会引起一个沿着角度坐标轴的圆形漂移值θ0。以图2（3）～图2（4）为目标，利用式（7）对其变换，结果见图4（a）与图4（b）。依图可知，经过式（7）处理后，除了水平轴方向存在周期性转变之外，图像中的其余内容大体相似。可见，将图像转变成对数极坐标域，能够增强算法对旋转变换的鲁棒性。

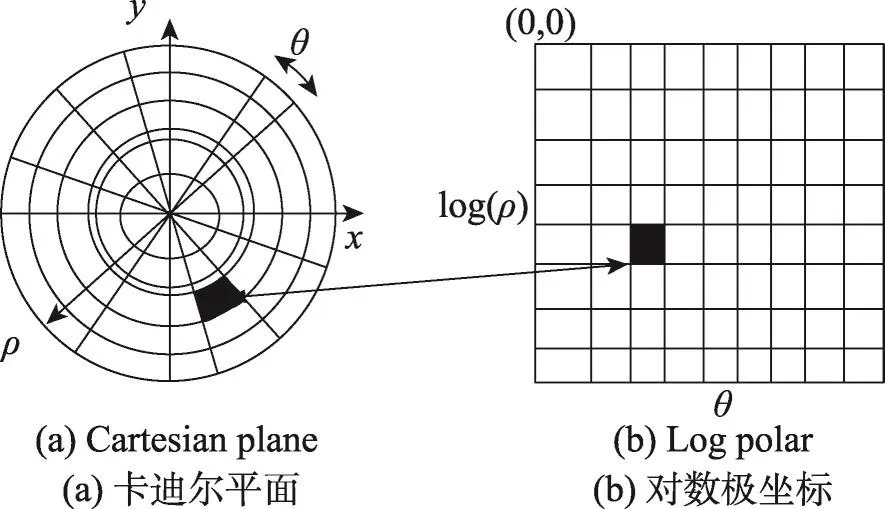
Fig.3 Cartesian coordinate mapping for log polar coordinates图3 卡迪尔坐标映射为对数极坐标

Fig.4 Secondary images after log polar transformation图4 对数极坐标变换后的二次图像

2.2.2 基于四元离散Fourier变换的图像特征提取

为了兼顾彩图的色度信息，提取鲁棒特性较好的特征，本文联合超复数理论[13]与经典Fourier变换[14]，建立四元离散Fourier变换机制。四元是超复数的一个扩展，包含1个实部与3个虚部：

其中，a、b、c、d均为实数；i、j、k为虚拟单元，满足如下条件：

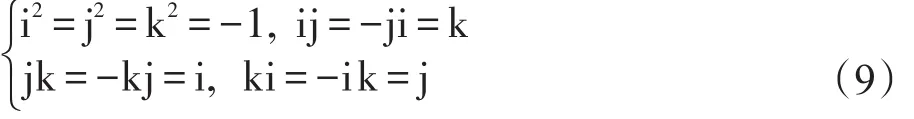
依据式（9）可知，四元数的乘法规则是不可互换的，则任意一个四元数的共轭与模量分别为：

由于彩色图像拥有3个分量R、G、B，将其视为虚部，则彩图f1(ρ,θ)为：

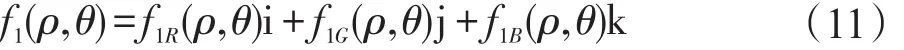
其中，f1R(ρ,θ)、f1G(ρ,θ)、f1B(ρ,θ)代表对数极坐标变换图像f1(ρ,θ)的3个分量。

基于上述超复数理论，将其用于经典Fourier变换[14]，建立四元离散Fourier变换机制：

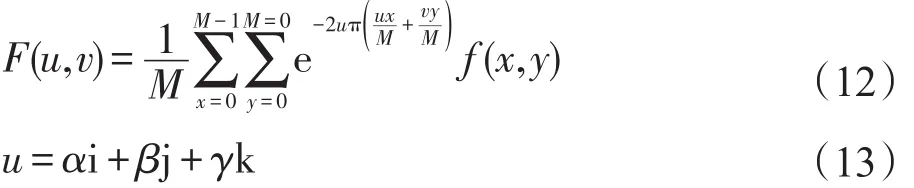
其中，u为纯四元数，且|u|=1；α、β、γ均为实数。

根据式（12），则其逆变换模型为：

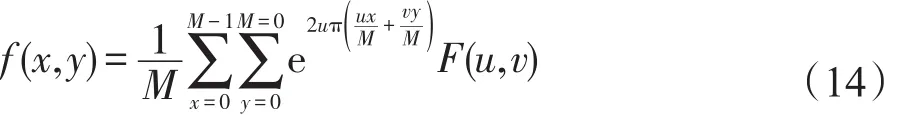
再依据式（7）与式（12），可得对数极坐标变换后的彩图四元离散Fourier变换：

其中，F0(u,v)、F1(u,v)分别为旋转前后的彩图四元离散Fourier变换的频域系数；(u,v)代表频域坐标；θ0代表旋转角度；M为彩图尺寸。

依据式（15）可知，|F0(u,v)|= |F1(u,v)|。换言之，f1(ρ,θ)及其旋转后图像的四元离散Fourier变换幅度信息具有旋转不变性。由于四元离散Fourier变换的低频分量占据整个彩图的大部分信息，本文将四元离散Fourier变换的低频系数的幅度视为所要提取的特征。例如，从其低频频谱中的方形区域选择P个幅度系数，若四元离散Fourier变换系数的中心坐标为u=129,v=129，且将低频幅度系数P的尺寸设为5×5，则所择取的低频系数范围是u,v∈[127, 131]。

2.3 图像哈希生成与认证

依据文献[15]可知，若图像哈希不经过加密处理，则攻击者可在保留初始哈希序列的同时，通过构建不同图像来篡改图像信息。为此，本文基于Logistic映射，设计位置扰乱机制。对低频系数进行加密处理，提高图像哈希安全性。若低频幅度系数为P1,P2, …,PN,再迭代Logistic映射，生成混沌序列{Xi}∶

其中，μ为控制参数，当μ∈[0,4]时，式（16）为混沌状态。

再对迭代式（16）得到的序列{Xi}进行升序排列，形成新的数组{Xi′}，并在{Xi}中找出{Xi′}对应元素的位置，形成位置序列{Yi}：

再利用式（17）对四元离散Fourier变换低频幅度系数进行置乱，形成新的系数序列{si}。

将加密后的低频幅度系数{si}转换成行矢量Z={z1,z2,…,zN}，N为图像低频系数个数，从而构建图像哈希模型：

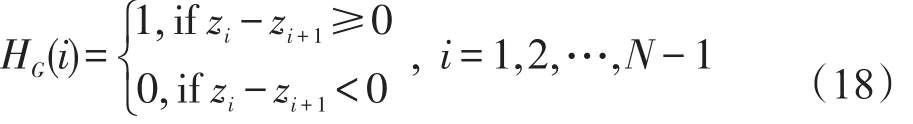
在实际应用场景中，初始图像I0是利用其自身的鲁棒哈希H0在网络中传输给用户，在接收端，用户可以依据哈希值来检测图像的真实性，完成图像内容认证。若接收图像I1，其在传输过程中可能被篡改，再根据本文哈希算法，计算I0、I1的哈希为H0、H1。引入归一化汉明距离D[16]，设计哈希相似度计算模型，来评估H0与H1的相似度：

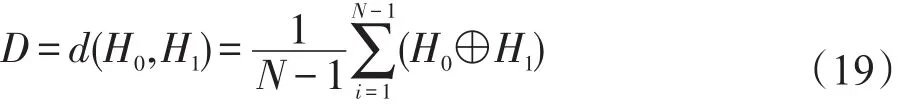
其中，N为低频幅度系数数量；⊕是异或运算。

依据式（19），当汉明距离D值小于预先设置的阈值λ时，则认为图像内容真实，未被篡改；反之，则认为图像在传输过程中被篡改。

2.4 时间复杂度分析

依据本文算法描述可知，其主要运算量是利用PED模型来预处理图像，利用对数极坐标变换与四元离散Fourier变换提取图像特征，基于Logistic映射的低频幅度系数置乱。若输入图像尺寸为M×N,则利用PED模型来预处理图像的复杂度为O(M×N),与文献[8]、文献[9]的图像预处理的复杂度相等；利用对数极坐标变换来平滑图像的复杂度为O(M×N),再利用四元离散Fourier变换提取彩色图像三分量的特征，其复杂度为,但是由于对数极坐标变换压缩了数据结构，降低了图像的冗余信息，最终使得四元离散Fourier变换的时间复杂度要远低于而文献[8]利用传统的Fourier变换提取彩色图像三分量特征的复杂度为O(3N2)，文献[9]利用高阶Zernike矩来提取彩图特征的复杂度为O(3qN2)（q为Zernike矩的阶数）；利用一维Logistic映射来置乱低频幅度系数，其复杂度为O(p)（p为四元离散Fourier变换提取的彩图低频系数的数量）。可见，相对于文献[8]、文献[9]而言，本文算法的时间复杂度较低。

3 实验结果与分析

为了测试本文图像哈希算法的鲁棒性，在UCID图像库[15]进行实验，该图像库包含1 338幅彩图，其尺寸有两种：512×384像素与384×512像素。同时，为了体现所提算法的优异性，将文献[8]基于离散傅里叶变换、文献[9]基于Zernike矩的哈希算法视为对照组。引入ROC特性曲线[16]来评估算法的认证性能，在该特性曲线中，其正确识别率PTPR与虚警率PFPR分别代表图像哈希的感知鲁棒性与识别能力：

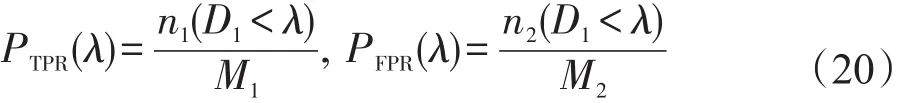
其中，n1代表将视觉上相同图像归类于相似图像的数量；n2代表将视觉上差异图像归类于相似图像的数量；M1、M2分别是视觉上相同图像与差异图像的数量。

依据本文算法描述可知，低频幅度系数的数量P与认证阈值λ对本文算法具有重要影响，为了获取更好的哈希鲁棒性，首先对二者进行优化确定。其余参数设置为：混沌控制参数u=3.5,X0=0.5，尺度因子。

3.1 低频幅度系数的数量P与认证阈值λ的确定

将UCID图像库[17]中的前1 000幅图像视为初始图像，每幅图像都进行如下篡改操作，见表1。

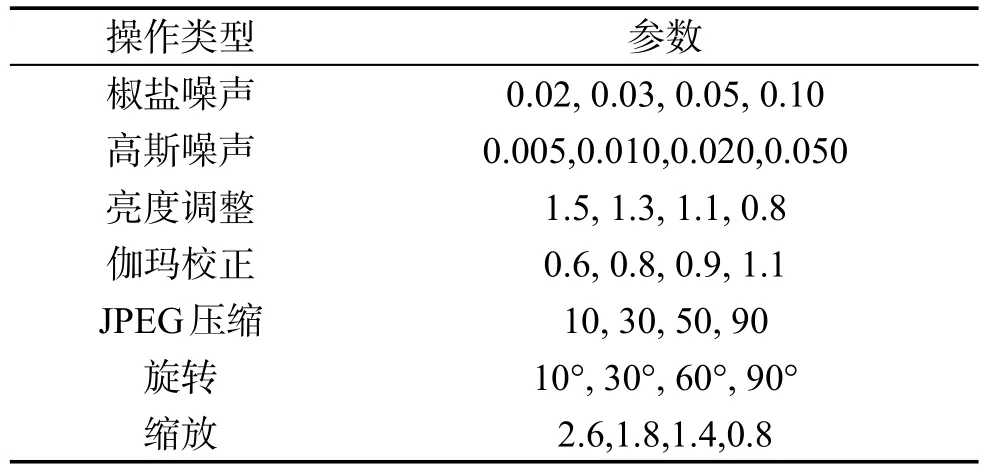
Table 1 Image content operation with different parameter values表1 不同参数值的图像内容操作

图像哈希的长度依赖于低频幅度系数的数量P，该值越小，则哈希感知鲁棒性越好，但是篡改识别能力较差。为了确定一个最优的P值，本文测试了不同P值对应的ROC特性曲线，结果见图5。随着P值的增加，ROC特性曲线越好，但是当P超过289时，其真阳性率开始下降。为了兼顾图像哈希的感知鲁棒性与识别能力，P值的取值应在[169, 289]内。为了获取较短的哈希长度，本文取P=152=225,依据式（18），则本文哈希H是224位。

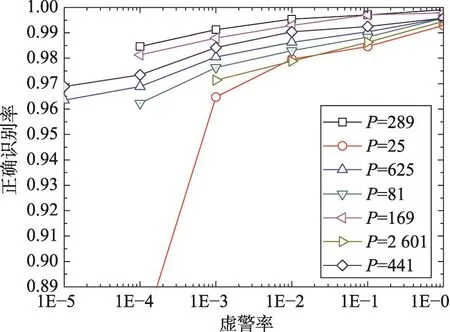
Fig.5 ROC curve test for the number of low frequency amplitude coefficients图5 低频幅度系数的数量P的ROC曲线测试

依据图6可知，对于不同图像，当汉明距离大于0.2时，其频率分布是不同的，而对于相同图像，当汉明距离小于0.2时，其频率分布存在较大差异，因此本文设置认证阈值λ=0.2。

3.2 哈希算法的鲁棒性对比测试

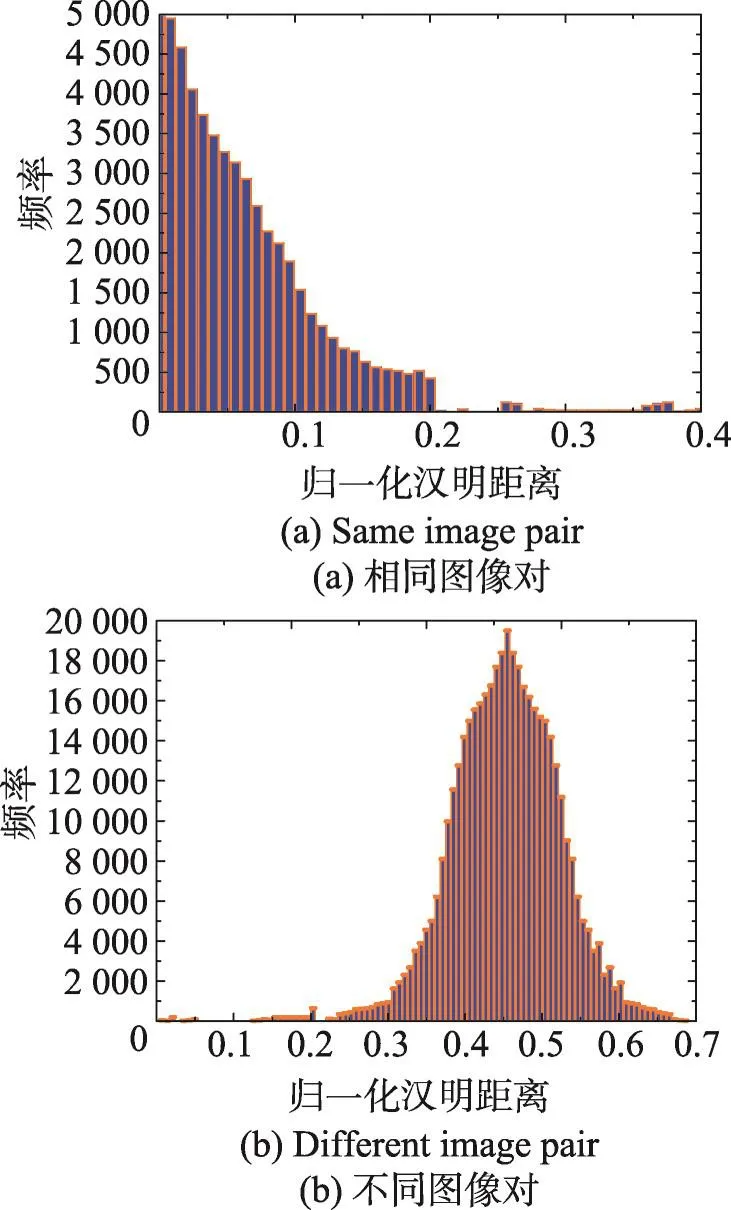
Fig.6 Distribution of normalized Hamming distanceD1图6 归一化汉明距离D1的分布

优异的哈希算法应具备以下关键特性：较强的感知鲁棒性、敏感性与安全性。根据2.1节，取P=225，λ=0.2进行实验测试。

3.2.1 感知鲁棒性测试

从UCID图像库中择取4幅彩图，见图7，且每幅图像都需经过表1中的7种数字操作，使得每幅图像形成60幅视觉相似图像，从而计算其归一化汉明距离，结果见图8。依图可知，对于这7种内容操作，本文哈希算法的归一化汉明距离都要小于0.2，这显示本文算法具有较强的感知鲁棒性。原因是本文算法的哈希是由四元离散Fourier变换的低频系数产生，兼顾了图像的色度信息，其相互关系很难被这些篡改形式所改变，且利用改进的PED模型与对数极坐标变换机制，增强了算法对缩放、噪声、JPEG压缩以及旋转等数字操作的鲁棒性。

3.2.2 敏感性测试

Fig.7 4 images in UCID dataset图7 UCID图像库中的4幅彩图

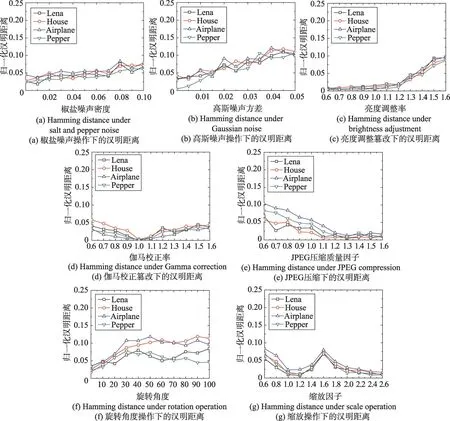
Fig.8 Perceptual robustness testing of Hash algorithm in this paper图8 本文哈希算法的感知鲁棒性测试

当图像被攻击者篡改时，其图像哈希会产生剧烈变化，与初始图像哈希截然不同。为了验证所提哈希算法的敏感性，本文测试了常见的移动-复制与缩放的组合篡改形式，见图9，并计算每一幅图像与初始图像间的归一化汉明距离，见表2。依表可知，这些篡改后的伪图像的归一化汉明距离均大于0.2，根据式（19）认证阈值的关系可知，本文算法能够认定这些图像的内容被篡改。可见，所提哈希算法具有较强的敏感性。原因是本文算法建立了四元离散Fourier变换机制，在同步处理彩图的三分量时，其低频幅度系数兼顾了亮度和色度信息。

Fig.9 Initial image and tampered image图9 初始图像与篡改图像

3.2.3 安全性测试

为了验证所提算法的安全性，本文测试3 000组错误密钥，其哈希距离分布见图10。依图可知，所有的哈希距离都要大于0.2。若攻击者不知道密钥与哈希算法，由于本文哈希长度为224位，则生成相同哈希的概率为(1/2)224；若攻击者知道哈希算法，但是不知道密钥，则其转化成224位的置乱问题。可见，本文哈希算法能够满足安全性的需求。

Table 2 Normalized Hamming distance of image tampering表2 篡改图像的归一化汉明距离

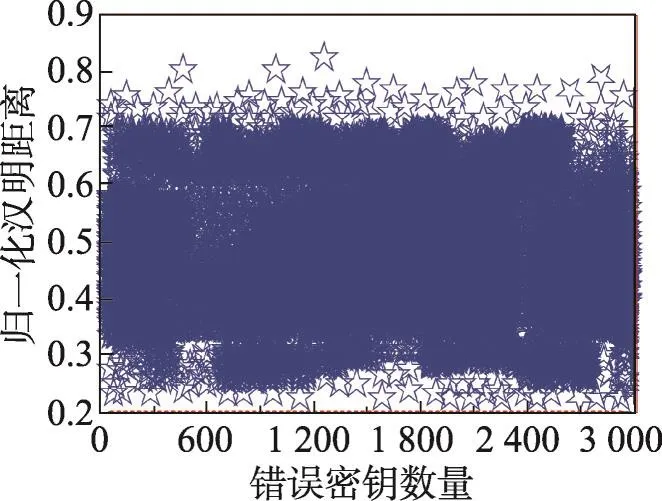
Fig.10 Security test of Hash algorithm in this paper图10 本文哈希算法的安全性测试

3.2.4 不同哈希算法的鲁棒性对比测试

在UCID图像库中抽取1 000幅彩图来生成相似图像对与不同图像对，通过测试本文算法、文献[8]与文献[9]3种算法的ROC特性曲线来评估。不同篡改攻击下的3种算法的ROC曲线见图11，各攻击条件下的识别率（图11（a）～图11（g））方差统计结果见表3。依图可知，面对表1中的7种类型的攻击，本文算法具有更好的ROC特性。例如，在椒盐噪声干扰下，当PFPR为0时，本文哈希算法的PTPR约为0.91，当虚警率PFPR为0.2时，其PTPR达到0.98。对其他另外6种攻击类型具有同样的特性。而文献[8]与文献[9]的鲁棒性不佳，略低于本文算法。文献[8]对旋转篡改的鲁棒性不高，在旋转干扰下，当PFPR为0时，二者的PTPR分别为0.81，当虚警率PFPR为0.2时，其PTPR达到0.92。而文献[9]对椒盐噪声与亮度调整篡改的鲁棒性不佳，在椒盐噪声干扰下，当PFPR为0时，二者的PTPR分别为0.83，当虚警率PFPR为0.2时，其PTPR达到0.93。另外，从表3中可以看到，对于表1中的7种攻击，本文算法的识别正确率的方差最小，而文献[8]、文献[9]两种技术的方差值均高于本文算法，这显示本文算法具有更好的稳定性。原因是本文算法利用改进的PED模型对其进行预处理，消除了噪声的干扰，并建立了四元离散Fourier变换机制与对数极坐标变换机制，利用其低频幅度系数来提取特征，使得该技术生成的哈希能够兼顾彩图的亮度与色度信息，其相互关系很难被旋转、亮度噪声等篡改形式所改变。而文献[8]是利用经典的离散傅里叶变换来获取彩图的哈希序列，丢弃了色度信息，难以识别旋转篡改；文献[9]利用局部特征与Zernike矩来生成哈希序列，虽然Zernike矩具有较好的旋转不变性，但是其所提取的特征忽略了色度信息，降低了算法的鲁棒性。

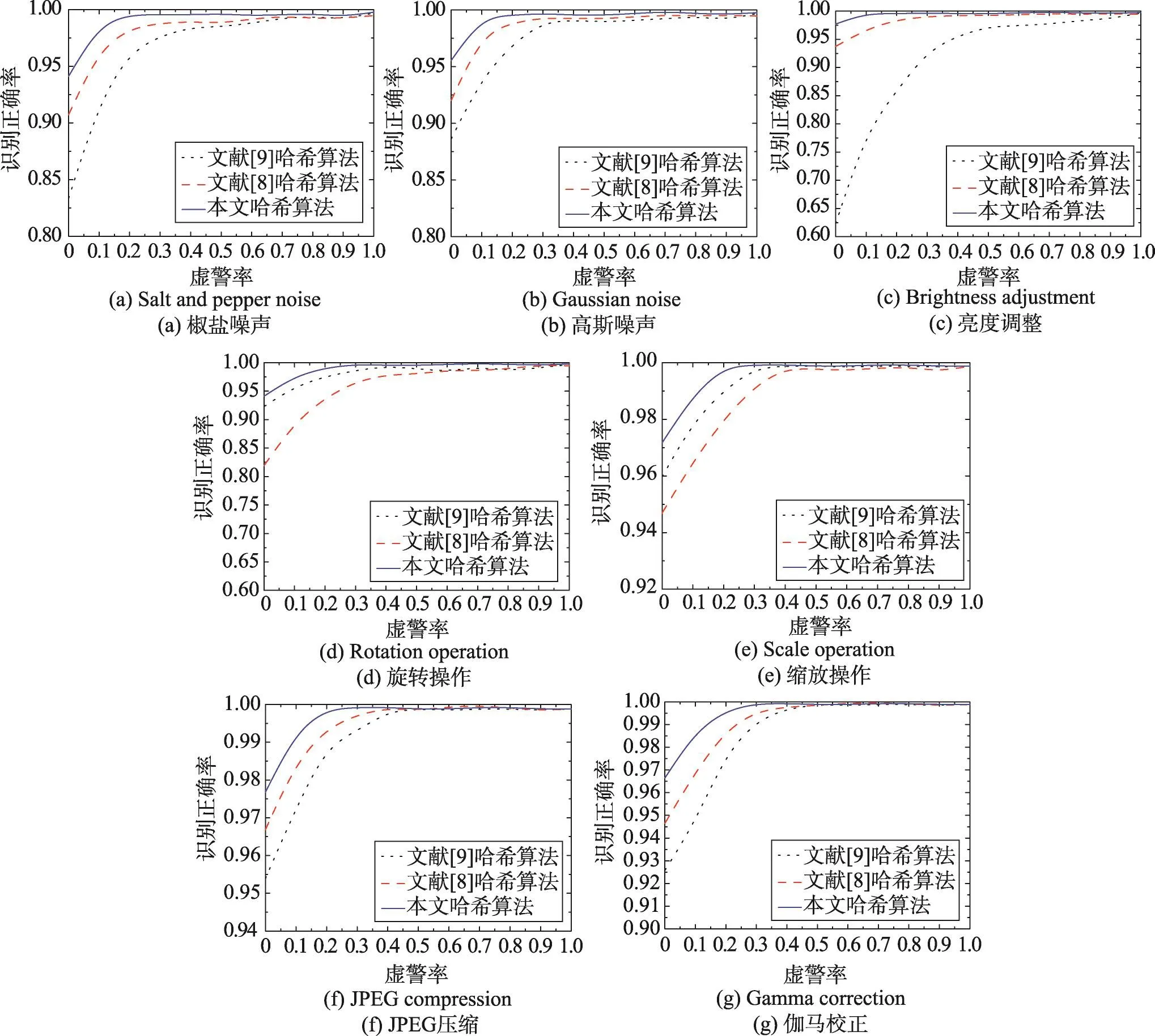
Fig.11 Hash ROC curve test of 3 algorithms图11 3种算法的哈希ROC曲线测试

3.2.5 不同哈希算法效率对比测试

为了体现本文算法、文献[8]与文献[9]3种算法的哈希生成效率，在微型机上进行Matlab测试，实验条件为酷睿3.5 GHz双核CPU,4 GB的内存，结果见表4。依表可知，本文算法由于建立了四元离散Fourier变换机制，能够同步处理彩图的R、G、B三分量，且只提取四元离散Fourier变换的低频幅度系数，从而有效降低了算法复杂度，其时耗为0.11 s；而文献[8]虽然也是利用Fourier变换的低频系数，但是该算法无法同步处理彩图的R、G、B三分量，使其时耗要高于本文算法，约为0.17 s；文献[9]虽然提取彩图的局部特征，同样地，该算法仍然是难以同步处理彩图的R、G、B三分量，需对每个分量逐一处理，算法时耗为0.21 s。

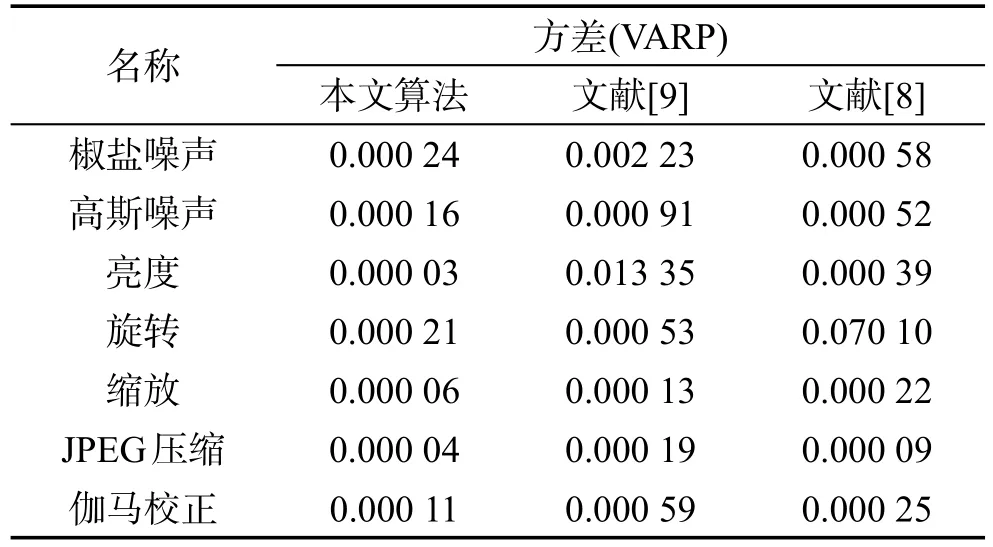
Table 3 Variance statistical results of recognition accuracy of 3 algorithms under various conditions表3 3种算法在各种条件下的识别正确率的方差统计结果

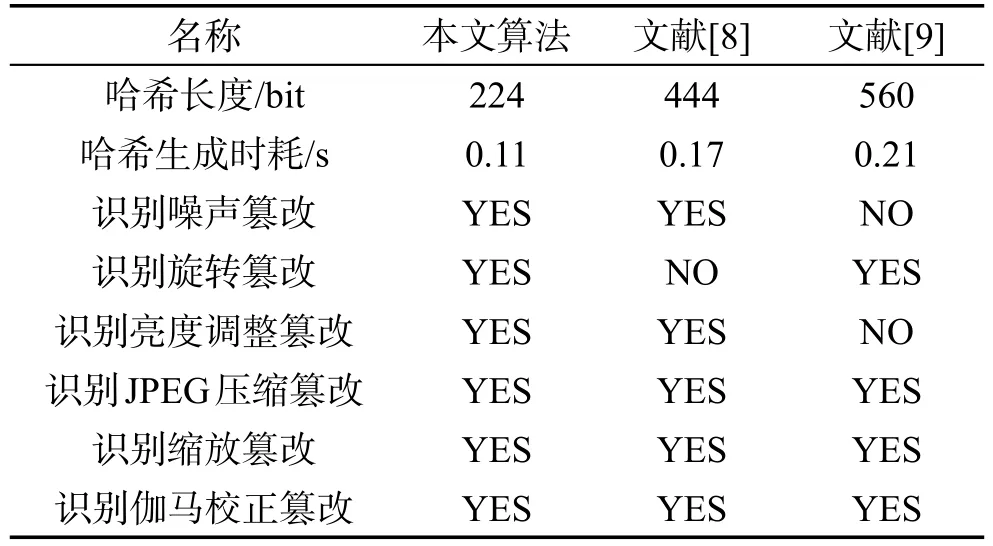
Table 4 Hash performance and efficiency test of 3 algorithms表4 3种算法的哈希性能与效率测试

4 结论

为了提高彩图哈希算法的鲁棒性与安全性，本文提出了超复数离散傅里叶变换耦合位置随机扰乱的彩色图像哈希认证算法。首先，利用改进的PED模型对输入图像进行预处理，增强算法对图像缩放的鲁棒性；利用对数极坐标变换，将其处理为二次图像；基于超复数理论与Fourier变换，建立四元离散Fourier变换机制，提取抗旋转篡改的图像特征；并基于Logistic混沌映射，设计位置扰乱机制，对四元离散Fourier变换低频幅度系数进行随机置乱；根据置乱后的幅度系数，构建图像哈希模型；引入汉明距离，评估初始图像与用户接收图像的哈希相似度，完成图像真伪认证。实验结果显示：与当前图像哈希算法相比，在处理彩色图像时，本文算法具有更强的鲁棒性与安全性，呈现出更好的ROC曲线特性。

[1]Siva P J,Vishnu M G,Gunda P K.Design of cryptographic hash algorithm using genetic algorithms[J].International Journal of Computer and Network Security,2010,2(10):133.

[2]Chauhan D,Kasat D,Jain S,et al.Survey on keypoint based copy-move forgery detection methods on image[J].Procedia Computer Science,2016,85(43):206-212.

[3]Hu Yuanyuan,Niu Xiamu.Image hashing algorithm based on robust bits extraction in JPEG compression domain[J].Information Technology Journal,2010,9(1):152-157.

[4]Chen Xi,Zhu Bing.Robust image hashing based on image normalization and Slant transform[J].Computer Engineering andApplications,2013,49(23):157-161.

[5]Zeng Yong,Sun Shusen,Xia Aijun.A perceptual image hashing algorithm based on image normalization and DCT[J].Journal of Zhejiang Sci-Tech University,2012,29(1):84-88.

[6]Tang Zhenjun,Zhang X Q,Dai Y M,et al.Perceptual image hashing using local entropies and DWT[J].Imaging Science,2013,61(2):241-251.

[7]Tang Zhenjun,Zhang Xianquan,Zhang Shichao.Robust perceptual image hashing based on ring partition and NMF[J].IEEE Transactions on Knowledge&Data Engineering,2014,26(3):711-724.

[8]Qin Chuan,Chang C C,Tsou P L.Robust image hashing using non-uniform sampling in discrete Fourier domain[J].Digital Signal Processing,2013,23(2):578-585.

[9]Zhao Yan,Wang Shuozhong,Zhang Xinpeng,et al.Robust hashing for image authentication using Zernike moments and local features[J].IEEE Transactions on Information Forensics&Security,2013,8(1):55-63.

[10]Ye Zhenhe,Li Xin,Li Ying.Visual and artistic images denoising methods based on partial differential equation[J].Journal of Multimedia,2013,8(3):284-290.

[11]Saini N,Sinha A.Optics based biometric encryption using log polar transform[J].Optics Communications,2010,28(7):34-43.

[12]Shao Hong,Zhu Hong,Cui Wencheng.Detection of image region-duplication forgery affected by flipping,rotation and scaling[J].Journal of Computer-Aided Design&Computer Graphics,2015,27(1):157-165.

[13]Li Ce,Xue Jianru,Tian Zhiqiang,et al.Saliency detection based on biological plausibility of hypercomplex Fourier spectrum contrast[J].Optics Letters,2012,37(17):3609-3611.

[14]Huang Liyan.Anti rotation transform image hashing algorithm[D].Guilin:Guangxi Normal University,2014:23-25.

[15]Sun Rui,Zeng Wenjun.Secure and robust image hashing via compressive sensing[J].Multimedia Tools and Applications,2014,70(3):1651-1665.

[16]Li Xinwei,Li Leida.Robust image hashing algorithm based on polar harmonic transform[J].Computer Simulation,2013,31(5):293-296.

[17]Schaefer G,Stich M.UCID—an uncompressed colour image database[J].Storage and Retrieval Methods and Applications for Multimedia,2003,5307:472-480.

附中文参考文献：

[4]陈曦,朱冰.结合图像归一化与Slant变换的鲁棒图像哈希[J].计算机工程与应用,2013,49(23):157-161.

[5]曾勇,孙树森,夏爱军.基于图像归一化和DCT的感知图像哈希算法[J].浙江理工大学学报,2012,29(1):84-88.

[12]邵虹,朱虹,崔文成.抗翻转、旋转和缩放攻击的图像区域复制篡改检测[J].计算机辅助设计与图形学学报,2015,27(1):157-165.

[14]黄丽艳.抗旋转变换的图像哈希算法[D].桂林:广西师范大学,2014:23-25.

[16]李新伟,李雷达.基于极谐变换的鲁棒图像哈希算法[J].计算机仿真,2013,31(5):293-296.

2016-07,Accepted 2016-12.

Hash Algorithm for Color Image Based on Super-Complex Fourier Transform Coupled with Position Permutation*

FENG He+,CHANG Guoquan,GUO Xiaobo
College of Computer Science and Information Engineering,Anyang University of Technology,Anyang,Henan 455000,China
+Corresponding author:E-mail:fenghe1982aygxy@sina.com

In order to solve these defects such as low detection accuracy and sensitivity of tampering contents,which are induced by converting three componentsR,G,Bof the color image into grayscale image for achieving image content authentication without considering the chrominance information in current image Hash algorithm,this paper proposes the Hash authentication algorithm for color image based on super-complex Fourier transform coupled with polar coordinate mechanism.Firstly,the input image is preprocessed based on the mean filter and the rotation factor to enhance the algorithm robustness of image scaling,so as to minimize the effect of image information loss on algorithm.Then the log polar coordinate transformation is introduced to transform the pretreatment image into the logpolar field.And the super-complex discrete Fourier transform is constructed by super-complex theory and Fourier transform to extract image features with anti-rotation tampering.The image Hash model is constructed according to the amplitude coefficients of the super-complex discrete Fourier transform.Meanwhile,the position disturbance mechanism is designed based on Logistic chaotic map,which randomly scrambles the image Hash for enhancing the security of Hash model.Finally,by using a cryptographic Hash model and the Hamming distance,the similarity of the two Hash values between the original image and the user received image is calculated.The experimental results show that,for processing color image,this algorithm has stronger robustness and security,it can effectively resist the color,contrast,rotation,noise and scale tampering attacks compared with the current image hashing algorithm.

image Hash;hyper-complex Fourier transform;log-polar transform;position disturbing mechanism;true and false information authentication;Hamming distance

10.3778/j.issn.1673-9418.1607051

*The National Natural Science Foundation of China-the Talent Training Joint Fund Project of Henan Province under Grant No.U1204613(国家自然科学基金-河南人才培养联合基金项目);the Science and Technology Research Program of Henan Province under Grant No.112106210128(河南省科技攻关计划);the Natural Science Foundation of Henan Province under Grant No.1412010401(河南省自然科学基金);the Science and Technology Research Program of Henan Province under Grant No.142102310188(河南省科技计划重点科技攻关项目).

CNKI网络优先出版:2016-12-16,http://www.cnki.net/kcms/detail/11.5602.TP.20161216.1049.002.html

FENG He,CHANG Guoquan,GUO Xiaobo.Hash algorithm for color image based on super-complex Fourier transform coupled with position permutation.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1837-1848.

A

TP391

FENG He was born in 1982.He is a lecturer at Anyang University of Technology.His research interests include image processing,information security and data mining.

冯贺（1982—），男，河南安阳人，硕士，安阳工学院讲师，主要研究领域为图像处理，信息安全，数据挖掘。

CHANG Guoquan was born in 1973.He is an associate professor at Anyang University of Technology.His research interests include computer image,information security and embedded system design.

常国权（1973—），男，河南安阳人，硕士，安阳工学院副教授，主要研究领域为图像处理，信息安全，嵌入系统设计。

GUO Xiaobo was born in 1976.He is an associate professor at Anyang University of Technology.His research interests include computer image,information security and intelligent optimization algorithm.

郭晓波（1976—），男，河南安阳人，博士，安阳工学院副教授，主要研究领域为计算机图像，信息安全，智能优化算法。