仿驼背鲸鳍机翼流动特性分析

祁武超，李东伟，田素梅

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

仿驼背鲸鳍机翼流动特性分析

祁武超，李东伟，田素梅

(沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

为研究前缘突节对机翼流动特性的影响，基于NACA0018标准翼型，对具有光滑前缘的标准机翼和具有不同前缘突节的仿生机翼分别进行了流动特性分析。结果表明，标准机翼在20°攻角之后，升力系数急剧下降，失速特性表现明显。而仿生机翼的升力系数也会在某一特定角度出现不同程度的下降，但下降趋势比较缓和。在大攻角下，仿生机翼的升力系数普遍大于标准机翼，可以有效的改善机翼的失速特性。相比于单位长度内的突节个数，突节的幅值对气动特性的影响更为明显。根据特定攻角下机翼表面流线的分布规律可知，波峰的存在使得其所在区域的流动分离相较于光滑前缘机翼发生了推迟，致使仿生机翼在大攻角下依然具有较大升力系数。

驼背鲸鳍；前缘突节；仿生机翼；流动特性分析；失速特性

当飞机飞行攻角过大时，很容易出现突然失速现象，造成严重的后果。提高飞机的失速攻角，一直是航空界需要克服的难题。

观察发现，海洋生物中的驼背鲸体型硕大，但是其机动性却相当灵活，在驼背鲸捕鱼进食的过程中，甚至经常做出接近90°角的向上冲刺的动作[1-2]，如图1所示。

图1 驼背鲸和其带有前缘突节的鲸鳍

Fish等[3]研究认为，驼背鲸鳍前缘突节的特殊结构是驼背鲸具有如此良好的水下性能的主要原因。Miklosovic等[4]通过对仿驼背鲸鳍机翼模型的风洞实验分析表明，该机翼模型的失速角比标准机翼的失速角延迟40%左右。Pedro等[5]通过数值模拟发现具有前缘突起的仿生机翼可以达到增加升力和减小阻力的效果，并且提出前缘突节结构可能类似于涡流发生器，从而改变边界层的分布情况，达到延缓失速的效果。Johari等[6-8]通过对不同前缘正弦曲线参数下的仿驼背鲸鳍模型进行风洞实验，得出前缘突节的幅值是影响大攻角下机翼气动性能的主要参数。之后他们又通过对流体染色的方式显示出当标准机翼表面流线出现大规模的分离时，仿驼背鲸鳍机翼表面依然有大量的附着流动。在对普通直翼进行实验研究的同时，Goruney等人[9]通过PIV技术对带有前缘突起的三角翼在失速攻角下近壁面的流动拓扑结构进行了研究，得出了在波长和幅值比值比较小的情况下，即便是很小的突节都能对近壁面流动拓扑结构产生很大的影响。Stanway[10]对带有前缘突起的机翼模型做了静态和动态的水动力分析，解释分析了仿驼背鲸鳍机翼能增大失速角的原因，他们认为前缘突节结构相当于一个漩涡制造器，产生小漩涡附着在机翼的上表面。Ernst A.van Nierop等[11]对仿驼背鲸鳍机翼建立空气动力学模型，通过对不同几何外形下产生的升力进行相关的运算，得出前缘突节的幅值对机翼特性有很大的影响而波长对机翼特性影响不大的结论。Amala等[12]对超音速和亚音速下仿驼背鲸鳍机翼进行了热应力的分析，结果表明，在大雷诺数下，仿生机翼表面的热应力分布随着前缘正弦幅值的增大而增大，但是并未指出仿生机翼和标准机翼在大雷诺数下升阻力系数的变化规律。Kim等[13]对前缘突节应用在三角翼上也进行了相应的实验研究，对该仿生机翼应用到现代先进战斗机上提供了一定的实验和理论依据。Hasheminejad等[14]对相同突节个数和相同前缘幅值的几组仿生机翼变换其前缘曲线类型。研究发现前缘突节的曲线类型同样是影响仿生机翼气动性能的主要因素，前缘突节为正弦曲线结构时性能达到最好。

在国内，金鸿章等[15-16]将驼背鲸鳍的前缘突节结构应用到船舶减摇鳍上，对其在水池进行实验，得出一定的实验数据和有效结论。针对国内外对仿驼背鲸鳍机翼研究所得出的实验结论，潘翀和陈皇等[17]提出了一种可变正弦前缘机翼方案，针对不同攻角相对应变换不同的前缘突节，有效提高了飞行器的航程和经济性。目前对仿驼背鲸鳍机翼的研究还处在起步阶段，针对前缘突起结构对机翼流动特性影响的规律并未达到统一的认识。因此有必要对该仿驼背鲸鳍机翼的流动特性做更进一步的探究。

1 数值模拟

1.1 模型建立和网格划分

选用NACA0018对称翼型作为研究模拟的对象。标准机翼基准弦长c=100 mm，展长s=105 mm，仿驼背鲸鳍机翼模型的前缘为正弦曲线，该正弦曲线的幅值A分别取2.5%c(即2.5mm)、5%c和10%c这3种情况。为了方便说明，对波长的研究按照前缘突节个数划分为2个突节和4个突节这两种情况。因此，不同的前缘幅值和突节个数组成了6个不同的仿驼背鲸鳍机翼仿生模型。用字母A、B命名，例如，A2.5B2表示前缘幅值为2.5mm，突节个数为2的仿生机翼；A5B4表示前缘幅值为5mm，突节个数为4的仿生机翼。如图2所示，图2a是标准机翼的三维效果图和俯视图，图2b～图2g是各个仿驼背鲸鳍机翼的俯视图。

图2 标准机翼和仿驼背鲸鳍机翼几何模型

采用C型拓扑进行非结构六面体网格的划分，计算域为上下边界距机翼前缘10c的半圆弧，出口边界距机翼后缘15c，翼展方向与机翼翼展尺寸相当，即105 mm。为了更好地研究大攻角后机翼附近的流体特征，各个模型均采用 RNGk-ε湍流模型和从粘性低层就开始计算的增强壁面函数(Enhanced Wall Treatment)，同时对机翼周围网格进行加密处理，首层网格高度满足y+=1。网格总数均在100万左右，满足计算要求。雷诺数Re=1.84×105,介质为一般气体，速度v=27m/s。

1.2 边界条件和计算方法的设置

计算域的各边界条件设置为速度入口，压力出口，机翼表面为无滑移壁面处理。采用SIMPLE迭代算法和二阶迎风格式。为了提高计算的准确性，迭代时间步长设置为0.0001。计算初始阶段选择默认的松弛因子，之后根据残差曲线的收敛和发散情况适当的调节松弛因子的大小，以提高计算速度和准确性。

图3 网格划分情况

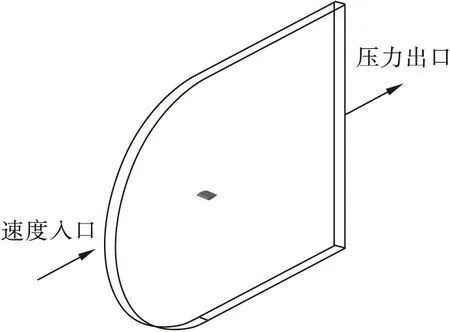
图4 计算域边界条件

2 计算结果分析

接下来介绍标准机翼以及具有前缘突起机翼在不同前缘幅值和不同前缘突节个数下计算出的升力系数和阻力系数变化趋势。随后将讨论选定的机翼在某些攻角下机翼表面流线的流动情况，以便更好地解释导致升力系数和阻力系数变化的原因。本文所有图中各个机翼的名称与图2所示相同。

2.1 前缘幅值对计算结果的影响

图5a和图5b所示的是标准机翼与前缘突节个数为2个和4个的情况下，不同的前缘幅值对机翼升力特性的影响。在攻角为0°～8°的范围内，所有机翼的升力系数基本上都随着攻角的增加而线性增长，相差不大。

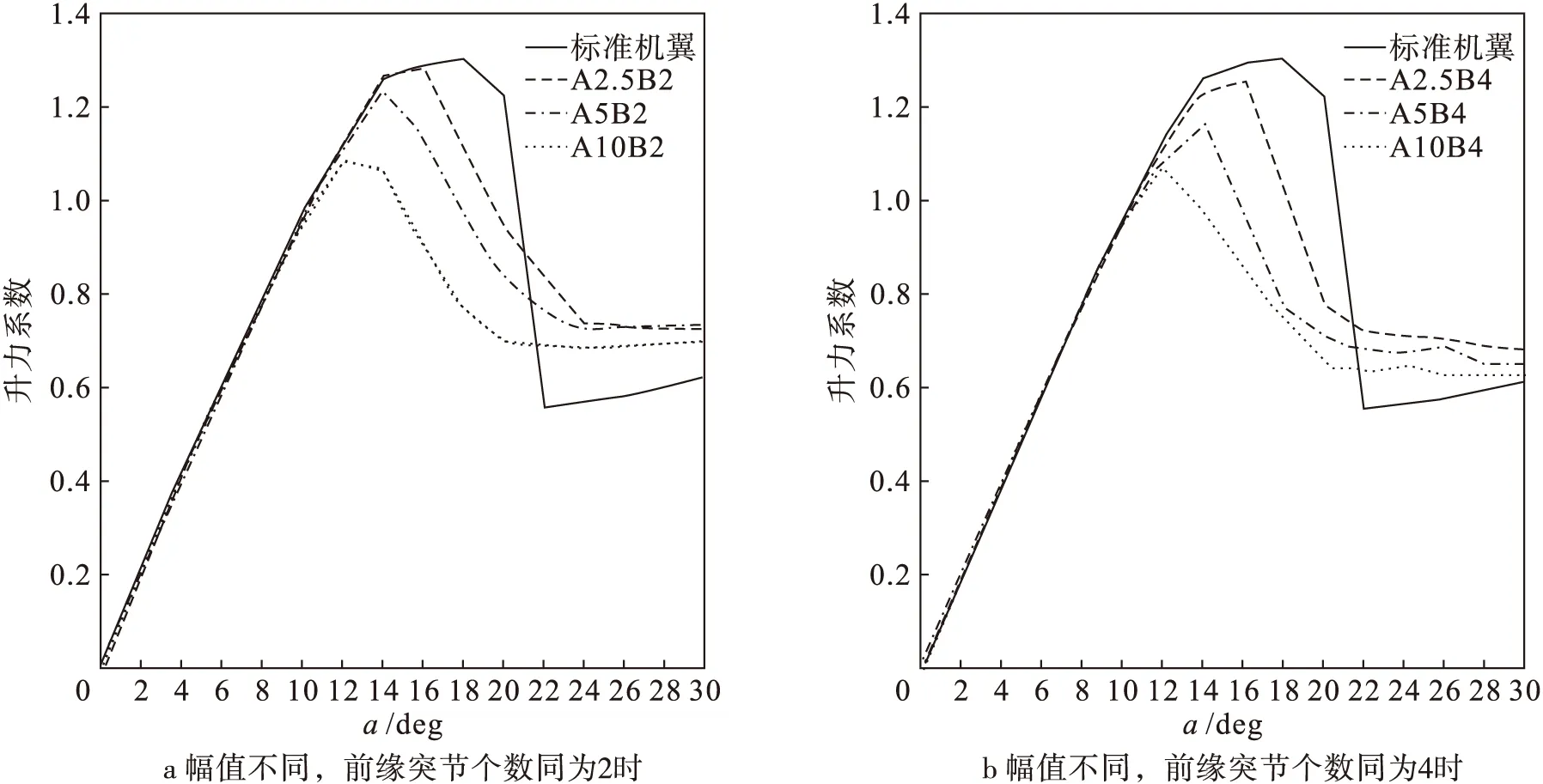
图5 升力系数变化曲线

标准机翼在α=8°～14°的范围内继续以一定的速率线性增加，到14°之后增加缓慢，并在α=18°处达到最大，最大升力系数CLmax=1.29。之后略微降低，在α=20°之后，升力系数迅速降低至0.56，出现失速状态。升力系数随着攻角的进一步增加而缓慢增加，但是一直保持在0.6以下。

对于前缘幅值为2.5 mm的A2.5B2机翼，升力系数在α=0°～16°范围内与标准机翼有着相同的变化规律，在到达最大升力系数CLmax=1.28之后，升力系数随着攻角的增加以一定的速率降低，降低速率远低于标准机翼。在α=24°之后保持恒定在0.74左右，大于标准机翼失速后的升力系数。A10B2机翼的升力系数在不同攻角下与上述机翼有着不同的变化趋势，其最大升力系数出现在α=12°，其中CLmax=1.08，明显小于标准机翼。之后升力系数同样出现下降的趋势，但在大攻角下升力系数始终大于标准机翼。具有中间前缘突起幅值(A5B2)的机翼的升力特性介于A2.5B2和A10B2之间。在攻角α=22°时，A5B2机翼的升力系数比标准机翼的升力系数高出48%。之后升力系数变化趋势与A2.5B2机翼基本相似，保持恒定在0.73左右。

图5b所示的是前缘突节个数为4时的机翼升力系数变化曲线，他们的升力系数与前缘突节个数为2的机翼有着非常相似的变化规律。最小前缘突起机翼(A2.5B4)的CL跟随标准机翼到α=16°时达到最大，最大升力系数CLmax=1.25。在α=22°时升力系数CL=0.73，之后随着攻角的增大而缓慢减低，但始终大于标准机翼。具有最大前缘突起(A10B4)机翼的升力系数随着攻角变化增加到CLmax=1.07，之后逐渐降低至CL=0.65，在α=20°之后达到基本恒定。中间幅值机翼(A5B4)升力系数在整个攻角范围内介于A2.5B4机翼和A10B4机翼之间。

图6a和图6b所示的是标准机翼与前缘突节个数为2个和4个的情况下，不同的前缘幅值对机翼阻力特性的影响。在攻角α=0°～12°范围内，带有前缘突节的仿生机翼阻力系数略大于标准机翼。在α≥12°时，标准机翼的阻力系数继续缓慢增加，当达到失速角度α=20°之后，阻力系数急剧增大。带有前缘突节的仿生机翼在α≥12°之后以更大的增长速率持续增加，仿生机翼始终具有比标准机翼更大的阻力系数。从图6中可以看出，在攻角α≥22°之后，前缘幅值为2.5 mm的机翼阻力系数更接近标准机翼。随着幅值的增加，对应攻角下的阻力系数也相应的增大，但增加幅度较小。

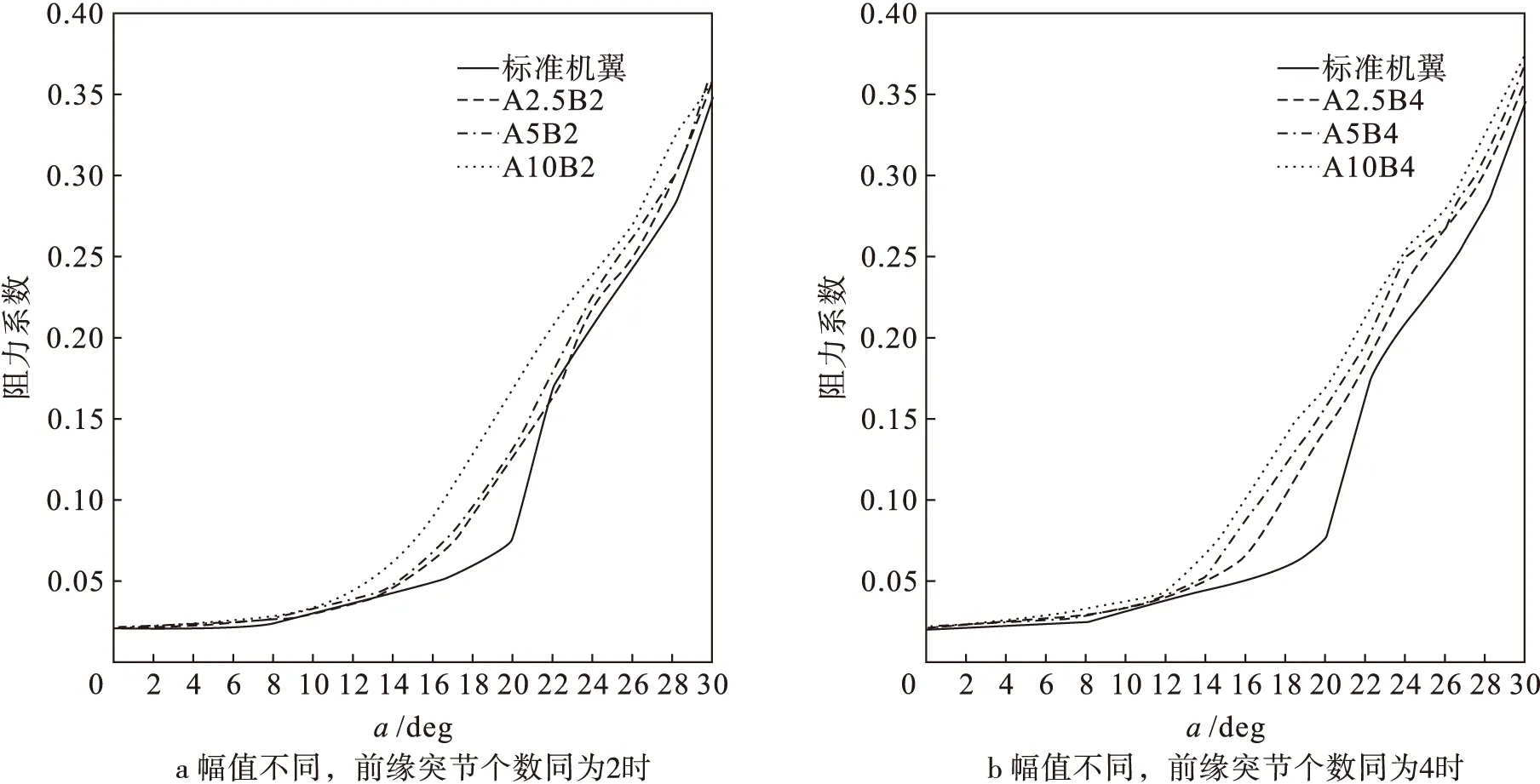
图6 阻力系数变化曲线

2.2 前缘突节个数对计算结果的影响

为了研究前缘突节个数的影响，将前缘幅值相同，突节个数不同的机翼作为一组进行比较。图7～9所示的是前缘幅值分别为2.5 mm、5 mm和10 mm时，不同前缘突节个数对机翼升阻力系数变化规律的影响。如图7a所示，当前缘幅值都为2.5 mm时，在α=0°～16°范围内，突节个数的增加对升力系数的影响并不是太明显，在α≥16°时，A2.5B4机翼的升力系数下降速率略大于A2.5B2机翼，并在α=22°之后基本保持恒定。除了在攻角α=20°～22°范围内，其余对应攻角下的升力系数相差不超过2%。如图8a所示，当前缘突节幅值为5 mm时，不同突节个数机翼升力系数变化的规律与幅值为2.5 mm时变化趋势相似，在攻角α=0°～16°范围内，升力系数几乎一样，当攻角α≥16°时，A5B2机翼和A5B4机翼的升力系数相差均在15%以内，且有着相似的变化趋势。如图9a所示，当前缘突节幅值为10 mm时，不同突节个数的机翼在攻角α≤22°范围内的升力系数相差不超过5%，在攻角α>22°之后，升力系数均保持相对稳定。在图7～9所示的各个阻力系数的变化曲线图中，前缘突节个数的变化对仿生机翼阻力系数影响较小，阻力系数接近重合，尽管如此，在大多数攻角下，具有较少突节个数的机翼产生比较多突节个数机翼稍微小的阻力。总体而言，在相同前缘幅值条件下的仿驼背鲸机翼中，前缘突节个数越多，使得相对应攻角下的升力系数有所减小，而阻力系数相应增加，因此在实际的工程应用中前缘突节个数不应该过多。

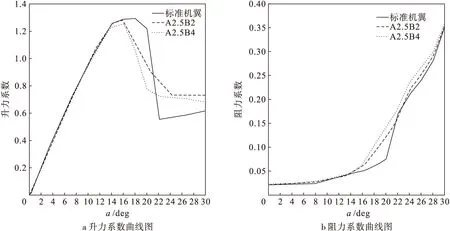
图7 突节个数不同，前缘幅值为2.5 mm时的升阻力系数变化曲线

图8 突节个数不同，前缘幅值为5 mm时的升阻力系数变化曲线

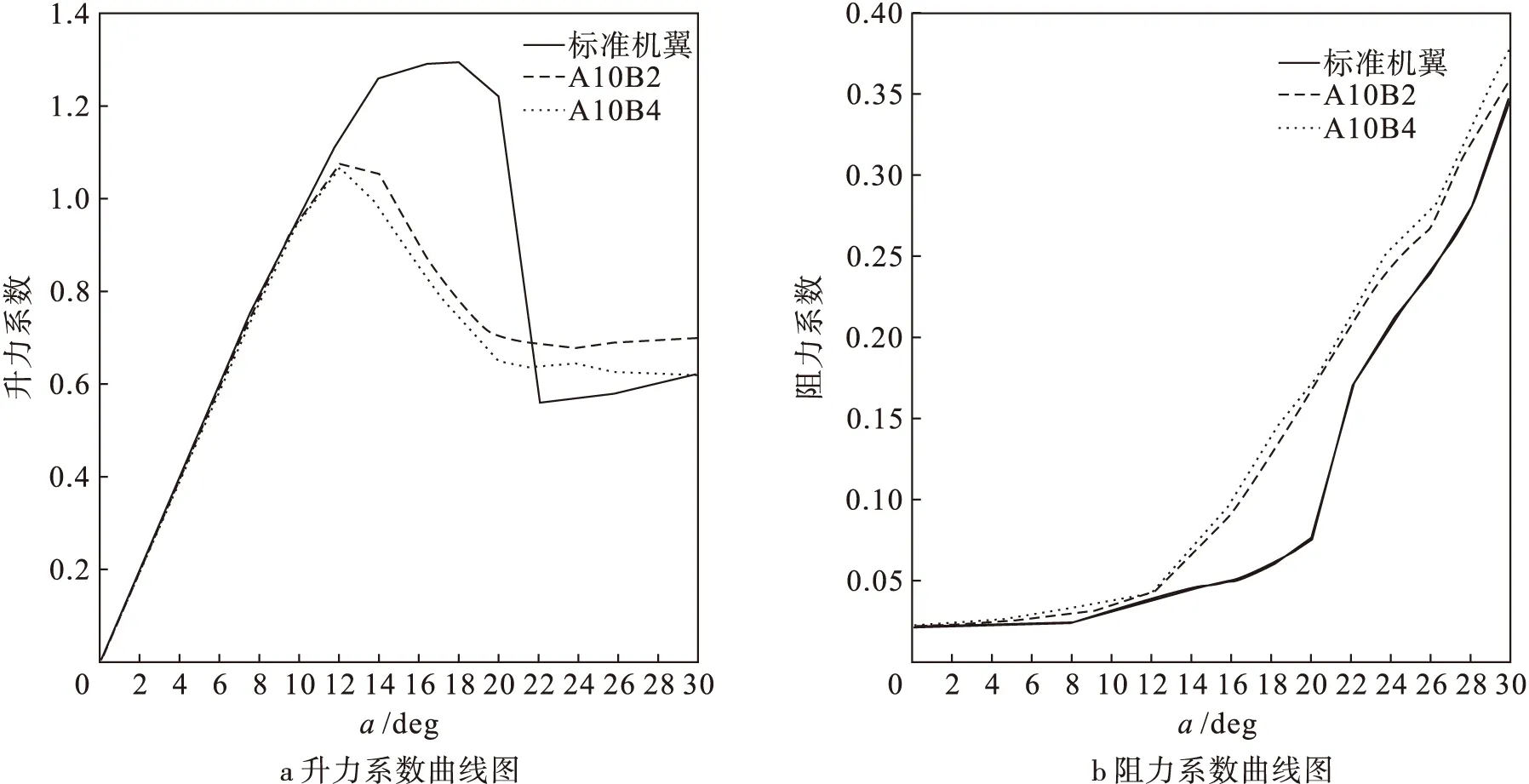
图9 突节个数不同，前缘幅值为10 mm时的升阻力系数变化曲线

2.3 机翼表面流线分布规律

为了解释仿驼背鲸鳍机翼延迟失速的原因，现在分别对Baseline标准机翼、A5B4仿生机翼、A2.5B4仿生机翼和A2.5B2仿生机翼在特定攻角下的机翼表面流线分布情况进行对比。选定攻角α=14°和α=24°作为未失速区域和失速区域的代表，如图10和图11所示。

图10 攻角α=14°时机翼表面流线图

由图10a和图11a可以看出，标准机翼表面基本没有任何展向方向的流动，流线在机翼表面先是附着在壁面附近流动，随后发生分离，分离区域为回流涡。机翼表面存在明显的分离线，分离线随着攻角的增大而不断地提前。在α=24°时，分离线已经处在机翼前缘的附近，使得机翼表面绝大多数处于分离流动区域。

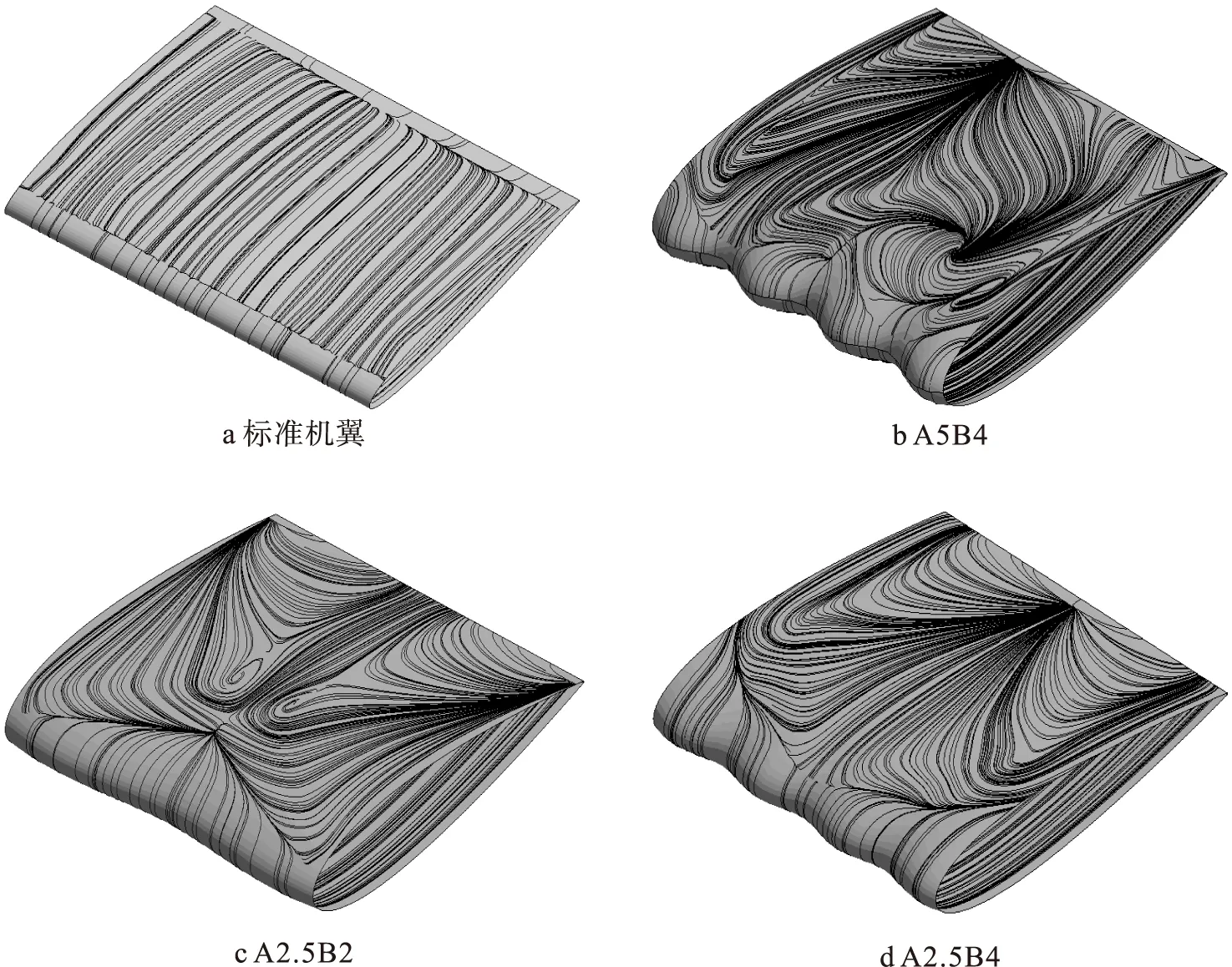
图11 攻角α=24°时机翼表面流线图

由于前缘突节的作用，流线在仿驼背鲸鳍机翼表面上存在明显的展向流动。在攻角α=14°时，机翼尾缘附近形成螺旋点，仿驼背鲸机翼的凸截面附近存在一股稳定的附着流线，而分离区流动相对紊乱。整体看来，在攻角为14°时，仿驼背鲸鳍机翼的分离区域总体大于标准机翼，在相同前缘幅值不同突节个数的A2.5B2和A2.5B4仿生机翼对比中，A2.5B4机翼表面的流线分离区略大于A2.5B2机翼。同样，在相同前缘突节个数不同前缘幅值的A2.5B4和A5B4仿生机翼对比中，A5B4机翼表面流线的分离区域大于A2.5B4机翼表面流线的分离区域。当攻角增大到24°时，标准机翼已经完全失速，而此时仿驼背鲸鳍机翼由于前缘突节的存在，导致机翼表面的流线分布发生展向的改变，形成小漩涡附着在机翼表面，存在一部分较大区域的附着流动，并且附着在各个仿生机翼表面的流线都处于凸截面的附近。因此整体而言，分离区域小于标准机翼，此时防驼背鲸鳍机翼的升力系数大于标准机翼。

3 结论

选用NACA0018翼型的机翼进行数值模拟,针对不同突节个数和不同前缘幅值的情况进行参照对比，得出结论如下。

(1)与标准机翼相比，仿生机翼在攻角较小的情况下并未表现出良好的气动性能，升力系数反而不如标准机翼，但差距不大。当攻角超过某一角度时，标准机翼出现突然失速状况，升力系数迅速降低。而此时仿驼背鲸鳍机翼的升力系数也出现不同程度的降低，但下降程度远低于标准机翼，且升力系数始终大于标准机翼的升力系数。由此看见，大攻角情况下(该处为α≥22°)，仿驼背鲸鳍机翼的气动特性要优于标准机翼。

(2)在仿驼背鲸鳍机翼前缘突节个数给定的情况下，前缘突节的幅值对机翼升阻力系数有较大的影响，幅值越大，机翼的升力系数越小。当具有相同的前缘突节幅值时，前缘突节个数越多，升力系数越小。因此较小前缘幅值和较少突节个数的仿生机翼可获得较好的升力特性。

(3)由于仿生机翼的前缘突节的影响，改变了流体在机翼表面的流动方式，使得在大攻角下，仿生机翼表面依然有很大的附着流动，波峰的存在使得其所在区域的流动分离相较于光滑前缘机翼发生了推迟，是致使仿生机翼在大攻角下依然具有较大升力系数的主要原因。

[1] FISH F E,BATTLE J M.Hydrodynamic design of the humpback whale flipper[J].Journal of Morphology,1995,225(1):51.

[2] FISH F E.Performance constraints on the maneuverability of flexible and rigid biological systems[C].Proceedings of the Eleventh International Symposium on Unmanned Untethered Submersible Technology,1999:394-406.

[3] WATTS P,FISH F E.The influence of passive,leading edge tubercles on wing performance[C].Proceeding of the Twelfth International Symposium on Unmanned Untethered Submersible Technology,2001:1-9.

[4] MIKLOSOVIC D S,MURRAY M M,HOWLE L E,et al.Leading-edge tubercles delay stall on hump-back whale (Megapteranovaeangliae) flippers[J].Physics of Fluids,2004,16(5):39-42.

[5] PEDRO H C,KOBAYASHI M.Numerical study of stall delay on humpback whale flippers[C].46th AIAA Aerospace Sciences Meeting and Exhibit,2008.

[6] JOHARI H,HENOCH C,CUSTODIO D,et al.Effects of leading-edge protuberances on airfoil performance[J].AIAA Journal,2007,45(11):2634-2642.

[7] JOHARI H,HENOCH C,CUSTODIO D.Visualization of flow on hydrofoils with leading edge protuberances[C].APS Division of Fluid Dynamics Meeting,2008.

[8] ZHANG M M,WANG G F,XU J Z.Aerodynamic control of low-reynolds-number airfoil with leading-edge protuberances[J].Aiaa Journal,2013,51(8):1960-1971.

[9] GORUNEYT ROCKWELL D.Flow past a delta wing with a sinusoidal leading edge:near-surface topology and flow structure[J].Experiments in Fluids,2009,47(2):321-331.

[10]STANWAY M J.Hydrodynamic effects of leading-edge tubercles on control surfaces and in flapping foil propulsion[D].Massachusetts Institute of Technology Master Degree of Science in Ocean Engineering,2008.

[11]VAN NIEROP E A,ALBEN S,BRENNER M P.How bumps on whale flippers delay stall:an aerodynamic model[J].Physical Review Letters,2008,100(5):054502.

[12]AMALA A.Aerothermodynamic Study on CleftedWing[J].International Journal of Current Engineering and Technology,2013,2(2):470-474.

[13]KIM H,KIM J,CHOI H.Effects of leading edge tubercles on the flow over a humpback whale flipper[C].APSMeeting.APS Meeting Abstracts，2013.

[14]HASHEMINEJAD S M,MITSUDHARMADI H,WINOTO S H.Effect of flat plate leading edge pattern on structure of streamwise vortices generated in Its boundary layer[J].Journal of Flow Control Measurement & Visualization,2014(2):18-23.

[15]金鸿章，潘艳，杨波.小攻角下驼背鲸减摇鳍的理论计算[J].船舶力学,2010,14(11):1219-1226.

[16]金鸿章，巩晋，李冬松.仿驼背鲸减摇鳍升力数值计算[J].中国造船,2009,50(4):22-27.

[17]潘翀，陈皇，王晋军.可变正弦前缘对直机翼气动性能影响的研究[J].实验流体力学，2013,27(4):7-11.

Analysisonflowcharacteristicofairfoillimitatingthehumpbackwhalefin

QI Wu-chao，LI Dong-wei，TIAN Su-mei

(Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136，China)

Based on the NACA0018 standard airfoil,flow characteristics of both standard wings with smooth leading edge and bionic wings with different leading edge protuberances were analyzed to study the influences of leading edge protuberances.The results show that the lift coefficient of the standard wing descended dramatically and the stall characteristic got obvious when the attack angle started to be higher than 20 degree.However,the lift coefficient of the bionic wing decreased by different extents corresponding to some specific attack angles,and the decreasing trend was slower.At high attack angles,the lift coefficient of bionic wings was generally higher than that of standard wings,which can improve effectively the stall characteristic of the wing.The effects of the amplitude of protuberances on the aero dynamic characteristics were stronger than that of the number of protuberances under unit length.According to the distribution of surface streamline under a specific attack angle,the appearance of peaks prolonged the flow separation during the corresponding region compared to the wings with smooth leading edge,resulting in the high lift coefficient of the bionic wings even at high attack angles.

humpback whale fins;leading edge protuberance;bionic wings;flow characteristics analysis;stall characteristics

2017-07-20

国家自然科学基金(项目编号：11502149)；青年成长基金(项目编号：201427Y);辽宁省教育厅系列项目(项目编号：L2015406)

祁武超(1982-)，男，河南漯河人，副教授，博士，主要研究方向：力学反问题，结构可靠性，E-mail：qiwuchao@sau.edu.cn。

2095-1248(2017)05-0026-09

TV19

A

10.3969/j.issn.2095-1248.2017.05.004

(责任编辑：吴萍 英文审校：赵欢)