基于鱼群算法的永磁体-电磁阀式磁流变阻尼器半主动悬架系统

胡红生 肖 平 江 明 欧阳青

1.嘉兴学院机电工程学院，嘉兴，3140012.安徽工程大学机械与汽车学院，芜湖，230031

基于鱼群算法的永磁体-电磁阀式磁流变阻尼器半主动悬架系统

胡红生1肖 平2江 明2欧阳青1

1.嘉兴学院机电工程学院，嘉兴，3140012.安徽工程大学机械与汽车学院，芜湖，230031

为了提高汽车悬架系统工作性能，对磁流变阻尼器半主动悬架控制系统进行了研究。首先，基于磁流变阻尼器工作原理，将永磁体与电磁阀引入其中，设计新型磁流变阻尼器并建立了仿真模型，示功特性试验结果表明，所设计的新型阻尼器可以满足汽车悬架的使用要求，同时，速度特性试验表明所建立的阻尼器模型具有较高的可信度;其次，基于牛顿定律建立了7自由度整车悬架模型；为了提高悬架控制效果，在对常规鱼群算法进行改进的基础上，设计了适合汽车悬架系统最优控制器的鱼群算法，实现了两者的集成控制;最后，进行了仿真试验。试验结果表明，与被动悬架相比，基于鱼群最优控制算法控制的汽车车身质心垂直加速度、俯仰角加速度、侧倾角加速度分别减小了38.95%、35.12%、35.98%，有效地提高了汽车的动力学性能。

磁流变阻尼器；永磁体；电磁阀；半主动悬架；鱼群算法

0 引言

随着磁流变技术的不断发展，磁流变减振器在车辆悬架系统中的应用已逐渐进入工程实用化阶段[1]。目前，传统的磁流变阻尼器通常采用线圈结构，通电产生感应磁场，继而控制输出阻尼力。传统结构的磁流变阻尼器虽能取得良好的减振效果，但仍存在一些亟待解决的问题，例如持续工作产生温升[2-3]、故障安全[4]、磁流变液静置沉降等[5]，从而制约了磁流变阻尼器在悬架应用上的进一步普及。为此，人们引入永磁体结构来产生阻尼力，以缓解传统线圈结构磁流变阻尼器所面临的以上问题。

已有学者对基于永磁体结构的磁流变阻尼器进行了探索性研究。TOPÇU等[6]为机械抓取装置设计了一种内置永磁体的线性磁流变阻尼器，并通过试验证明，该磁流变阻尼器具有良好的性能。 BÖSE 等[7-8]研发了含有永久磁体和线圈的新型磁流变阻尼器。CHOI等[9]设计了一种自供电式的内置永久磁体磁流变阻尼器，并对产生的电流与减振性能之间的关系进行了研究。YAN等[10]开发了一种基于永久磁体和线圈的可逆磁流变阻尼器，并通过试验证明，该新型磁流变阻尼器能对系统所需阻尼力作出快速反应。以上研究大多采用控制永磁体的位置或者结合电磁线圈结构来控制磁场大小，从而实现阻尼力的可控。

笔者将永磁体结构设计与电磁阀技术相结合，针对汽车悬架应用背景，设计了新型的永磁体-电磁阀式磁流变阻尼器。阻尼通道内磁场由永磁体单独提供，通过调节电磁阀开度来调节阻尼力。本文首先针对所设计的新型阻尼器进行示功特性和速度特性试验；在此基础上，建立了包含新型阻尼器的悬架模型和电动助力转向系统模型；结合改进的鱼群算法和最优控制算法，设计了适合半主动悬架控制的鱼群最优控制算法，并针对多种工况进行了仿真试验，以验证该算法的有效性。

2 永磁体-电磁阀式磁流变阻尼器建模与试验

2.1永磁体-电磁阀式磁流变阻尼器结构

本文设计的永磁体-电磁阀式磁流变阻尼器结构示意图见图1，它主要由活塞杆、活塞头、内筒、外筒、流量控制阀等组成。内筒与外筒中充满磁流变液。永磁体安装于工字形导磁活塞头的凹槽内，并以环氧树脂密封，其极性如图1所示。活塞头外侧与内筒之间形成阻尼通道。为保证永磁体所产生的磁场垂直通过阻尼通道，活塞头两侧各有一个不锈钢阻磁盘。活塞头将内筒分为左、右两腔，内筒左腔壁上有若干流液孔，磁流变液可以通过该孔在内筒与外筒间自由流动。内筒和外筒底部有管道相连，磁流变液可以在内外筒间流动，其通断受缸筒底部的流量控制阀控制。流量控制阀由螺钉以及缠绕在螺钉杆上的线圈、阀芯、复位弹簧、导向块等组成。螺钉与线圈组成电磁体可以对阀芯产生吸引，与复位弹簧及导向块配合后可以打开或关闭阀门。

永磁体-电磁阀式磁流变阻尼器的工作原理是：收缩行程中，活塞向右运动，右腔液体受挤压从而压力增大，一部分液体通过流量控制阀流入外腔，再经外腔进入左腔，其余液体通过阻尼通道流入左腔；同理，在复位行程阶段，液体亦通过流量阀及阻尼通道两种方式流入右腔。流过流量控制阀的液体不受永磁体磁场的影响，因而不产生库仑阻尼力；而通过阻尼通道的液体在永磁体磁场作用下发生磁流变效应，产生相应的库仑阻尼力。由于阻尼通道的阻尼力与流经通道的液体体积有关，故可通过调节阀芯的开度来控制通过阻尼通道和调节阀的流量，从而实现输出阻尼力的可控性。

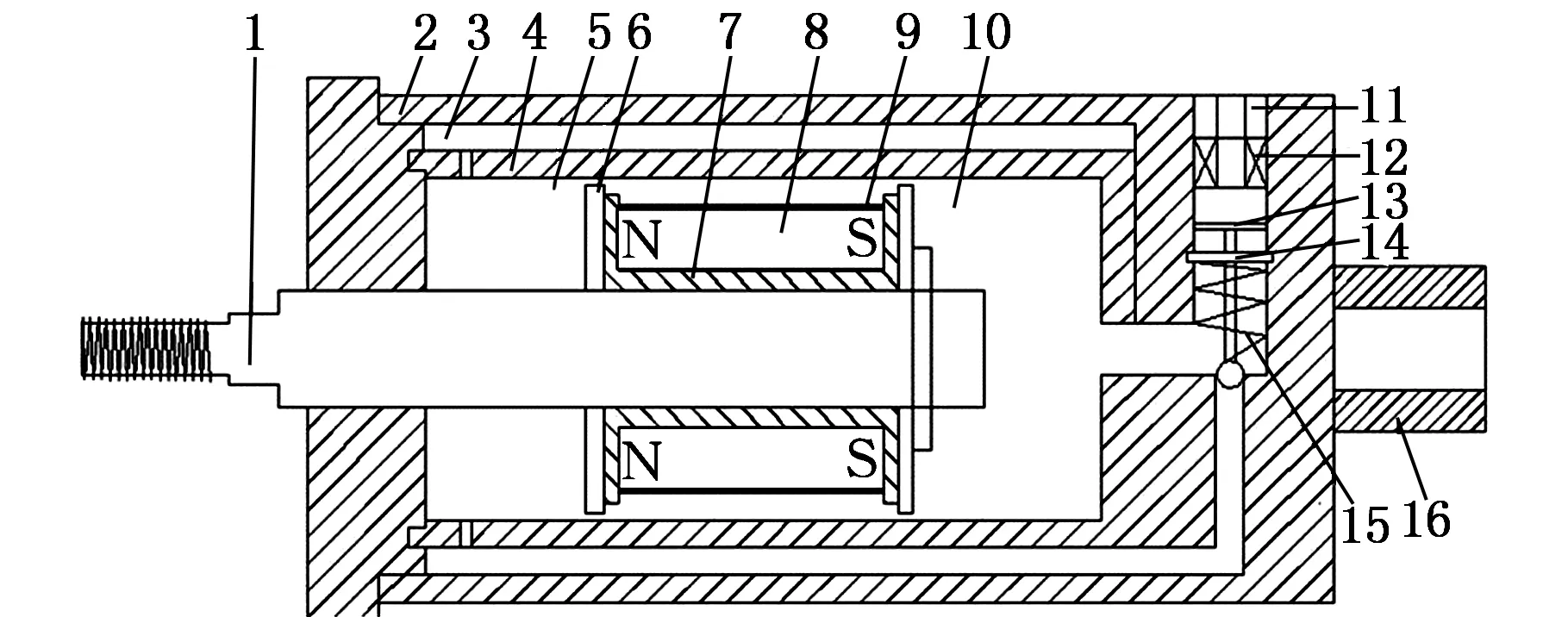
1.活塞杆 2.外筒 3.外筒与内筒之间管道 4.内筒 5.内筒左腔 6.活塞 7.工字形导磁铁 8.永磁体 9.阻尼通道 10.内筒右腔 11.螺钉 12.线圈 13.阀芯 14.导向块 15.复位弹簧 16.阻尼底座图1 永磁体-电磁阀式磁流变阻尼器结构示意图Fig.1 Structure diagram of magnetorheological damper with novel twin-tube

2.2阻尼器建模

设在运动过程中，从流量控制阀和阻尼通道流过的磁流变液体积流量分别为qV1、qV2，则活塞在运动过程中排开磁流变液总和

qV=qV1+qV2

(1)

根据阻尼器工作原理，有

qV=π(r1-r2)2v

(2)

式中，r1、r2为活塞头与活塞杆的半径；v为活塞头与缸筒的相对速度。

当线圈通电时，阀芯被吸引，移动距离为l，则气隙体积减小量

dV0=2Sdl

(3)

式中，S为铁芯截面积。

设气隙中的磁感应强度为B，则气隙里储存的磁场能量减少量

dW0=(B2Sdl)/μ0

(4)

式中，μ0为空气导磁率。

dW0转变为机械功，即

(B2Sdl)/μ0=Fdl

(5)

式中，F为磁极产生的吸力。

设弹簧刚度系数为k，则此时弹簧上产生的弹力为F1，有

F1=kl

(6)

由力平衡原理可得

F1=F

(7)

设通电线圈的电流强度为I，则气隙磁感应强度

B=NIμ0/l

(8)

式中，N为线圈匝数。

结合式(5)～式(8)，可得

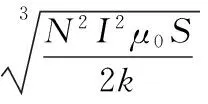
(9)

根据流体力学知识，有

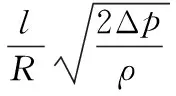
(10)

式中，Cd为流量系数；d为阀座孔直径；Δp为压差；R为钢球半径；ρ为磁流变液密度；h0为系数。

对于球阀，有

(11)

将式(11)代入式(10)可得

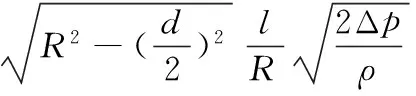
(12)

下面计算阻尼通道内任一点P(x0,y0,z0)的磁感应强度H′。由于永磁体为沿轴向均匀充磁的圆柱形永磁体，故其正负磁荷分别位于圆柱永磁体的上下端面；上下端面分别用S+、S-表示，面S+、S-上任一点分别用P′(x′,y′,H)与P″(x″,y″,0)表示；以永磁体下端面圆柱中心为圆点，以圆柱体轴线为z轴，建立位于直角坐标系的永磁体磁场示意图，见图2。于是，根据毕奥萨伐尔定律和标量磁位的原理，阻尼通道内任一点的磁感应强度[11]：

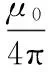
(13)

其中，r为阻尼通道内任一点到S上任一源点的矢量，r+为阻尼通道内任一点到源点的距离。有

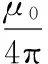
(14)

其中，r+与r-分别表示阻尼通道内任一点到磁源上下端面任一源点的矢量，r+与r-分别表示阻尼通道内阻尼通道内任一点到磁源上下端面任一源点的距离。

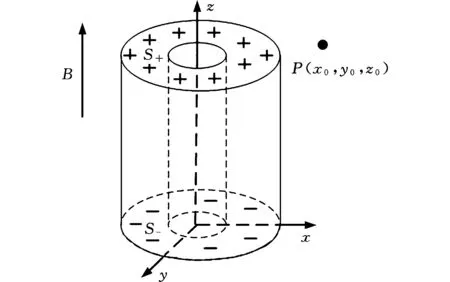
图2 永磁体磁场示意图Fig.2 Schematic diagram of magnetic field of permanent magnet

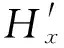
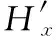
(15)

(16)

(17)

A1=[(x0-Rcosθ)2+(y0-Rsinθ)2+(z0-L)2]3/2

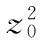
式中，R1、R2分别为永磁体的内径和外径；L为永磁体长度。

设在阻尼通道内所取的点关于y轴对称，则有

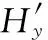
(18)

则在阻尼通道处的磁场强度

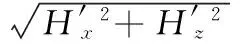
(19)

在活塞头两端阻磁盘的作用下，H′的方向垂直于磁流变液流动的方向。

由磁流变液性质可得其屈服应力

τy=λ1Hλ2

(20)

式中，λ1、λ2为磁流变液有关参数。

基于Bingham模型[12]的磁流变阻尼器阻尼力

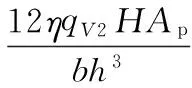
(21)

式中，b为平板宽度；h为阻尼通道宽度；Ap为活塞截面积。

将式(1)代入式(21)可得

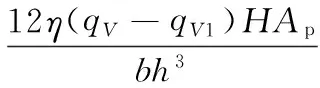
(22)

由式(9)、式(12)、式(22)可知，通过调节流量控制阀处电磁线圈的输入电流，即可调节永磁体-电磁阀式磁流变阻尼器阻尼力。

2.3阻尼器试验

为了检验阻尼器工作性能及阻尼器模型的准确性，以奇瑞汽车股份有限公司的某款轿车前减振器使用标准进行加工后，采用上海北阅机械设备有限公司生产的20 kN电液伺服悬架试验台对阻尼器进行示功特性试验，如图3所示。试验采用正弦波输入，最大速度为0.55 m/s，振幅为±50 mm，测试频率为1.68 Hz。

图3 动态特性测试系统Fig.3 Dynamic performance testing system

图4 示功曲线Fig.4 Indicator diagram of MR damper

阻尼器示功曲线如图4所示，当电磁阀输入电流为1.2 A时，示功图包围面积较小；当电磁阀输入电流为0时，示功图包围面积最大，最大阻尼力可达1500 N以上,这是由于当电磁阀输入电流减小时，电磁阀的开度减小导致更多的磁流变液从阻尼通道通过，于是产生的阻尼效果好。同时，随着电磁阀输入电流的减小，示功图的面积在逐渐增大，这表明减振器的减振效果良好，设计的永磁体-电磁阀式磁流变阻尼器具有较强的可控性。

对上述永磁体-电磁阀式磁流变阻尼器的理论模型进行计算分析,并与减振器台架试验结果进行比较，得出电磁阀输入电流分别为1.2 A、0.6 A、0时的速度特性曲线，如图5所示。由图5可见，模型模拟的数值与试验值基本吻合，说明所设计的理论模型是正确的。

图5 速度特性曲线Fig.5 Speed characteristic curve of MR damper

3 车辆系统模型的建立

3.1整车模型

以7自由度整车系统为研究对象，其物理模型如图6所示。根据该物理模型建立整车振动数学模型。

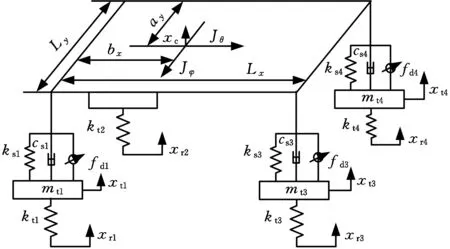
图6 整车物理模型Fig.6 Vehicle physical model

由于车身的俯仰角和侧倾角变化较小，故可得7自由度整车悬架系统的运动方程[13-14]：

(1)车体的垂向运动方程为

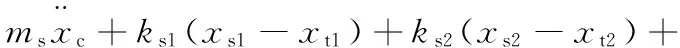
(23)

(2)车身俯仰运动方程为

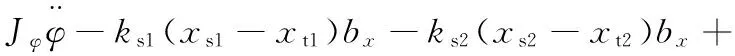
(24)

(3)车身侧倾运动方程为

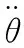
(25)

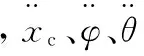
3.2路面模型

采用一个滤波白噪声作为路面输入模型：

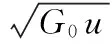
(26)

i=1,2,3,4

式中，G0为路面不平度系数；wi为均值为零的Gauss白噪声；f0为下截止频率。

4 鱼群-最优控制算法设计

就7自由度整车模型而言，要充分考虑行驶安全性、汽车平顺性以及操纵稳定性。系统的主要性能指标有车身侧倾角和俯仰角、车身垂直加速度、悬架动行程、轮胎动位移等。就7自由度整车悬架系统的控制而言，最优控制算法能以权值的方式将所有指标考虑其中，有效提高系统的综合性能。所设计的最优控制性能指标

(27)

式中，xri(i=1,2,3,4)分别为各轮所受的路面激励位移；aj(j=1,2,…,11)为最优控制器的加权系数；ri为4个车轮动载荷调节加权系数；Q为状态加权矩阵；R为控制加权矩阵；Fd为力加权矩阵。

采用最优控制算法对整车悬架系统进行控制可以显著提高系统综合性能，但是最优控制器的加权系数很难通过经验来确定，为此，需要设计高效的采用寻优算法对其进行优化。鱼群算法具有稳健性强、对初值敏感性小、简单、易实现等优点，已有学者成功将其应用于路径规划、PID算法的优化、机场地面等待优化等，取得了良好的效果，但该算法也存在收敛速度慢、容易陷入局部最优等缺点。针对上述缺点，本文对常规鱼群算法进行改进设计，在此基础上设计适合于整车悬架系统控制的新型鱼群-最优控制算法。具体改进如下：①为了加快寻优速度，将解空间划分成n个子空间，采用n个小规模鱼群同时对解空间进行搜索；②为了提高寻优精度，采用随迭代次数增加而减小的自适应步长。

采用改进的鱼群算法对最优控制器的加权系数进行寻优，从而设计适合于整车悬架系统控制的鱼群-最优控制算法，其原理如下：将系数a1,a2,…,a11可能的取值范围确定的空间作为鱼群觅食的池塘空间，空间中的每个点代表寻优算法的一个解，解的优劣通过适应度函数(采用最优控制性能指标J表示)计算得到；通过鱼群的不断运动寻优，鱼群最终集聚在几个极值点附近。结合常规鱼群算法，本文设计的鱼群-最优控制算法步骤如下。

(1)初始化。设定最大步长为Sstep。

(2)公告板初始化。本文适应度函数采用最优控制性能指标及式(27)表示。

(3)执行聚群行为。判断中心位置的适应度Yc是否满足关系式Yc/nf>δYi，其中，nf表示搜索邻域内鱼群伙伴数目；δ表示鱼群拥挤度因子；Yi为鱼群当前位置食物浓度，即目标函数值。若满足则表示鱼群中心位置有较多食物且不拥挤，继而按下式

(28)

向中心前进一步；否则转向步骤(5)。其中，Xi、Xi+1、Xc分别为鱼群当前位置、人工鱼移动后的位置及目标点位置；rand( )产生0～1的随机数；rand()Sstep表示人工鱼移动范围为0～Sstep；(Xc-Xi)/‖Xc-Xi‖规定了人工鱼移动方向。

(4)执行追尾操作。在每个子群中，若人工鱼当前位置为Xi，其感知范围内最优鱼Xmax有最高食物浓度且不太拥挤，则令Sstep=rand()‖Xc-Xi‖，向该最优人工鱼移动一步；否则转到步骤(5)。

(5)执行觅食操作；在每个子群中，选择当前人工鱼(位置Xi)感知范围内某一随机状态Xj，若其适应度Yj>Yi，则以式(29)向其移动一步，否则若在尝试m次后仍不能满足，则按式(30)随机执行一次。

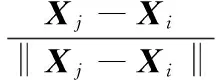
(29)

Xi+1=Xi+rand()Sstep

(30)

(6)判断是否达到最大迭代次数，若是则执行步骤(7)，否则转向步骤(3)。

(7)比较输出最大公告板信息，即最优值。

鱼群最优控制算法对磁流变阻尼器悬架系统控制的具体实现结构如图7所示。

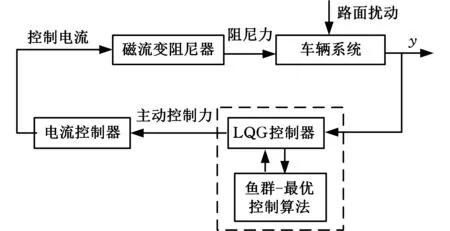
图7 磁流变阻尼器悬架系统控制的具体实现结构Fig.7 Implementation structure of MR suspension control system

5 仿真试验

采用MATLAB/Simulink建立所研究的永磁体-电磁阀式磁流变阻尼器7自由度整车悬架系统模型及基于鱼群-最优控制算法的控制器模型并进行仿真试验。仿真中，车速为20 m/s，截止频率为f0=0.01 Hz，不平度系数G0=5×10-6m3。转向行驶时，各车轮处路面输入互不相关，且均为白噪声信号。仿真车型参数见表1，鱼群算法参数设置见表2。

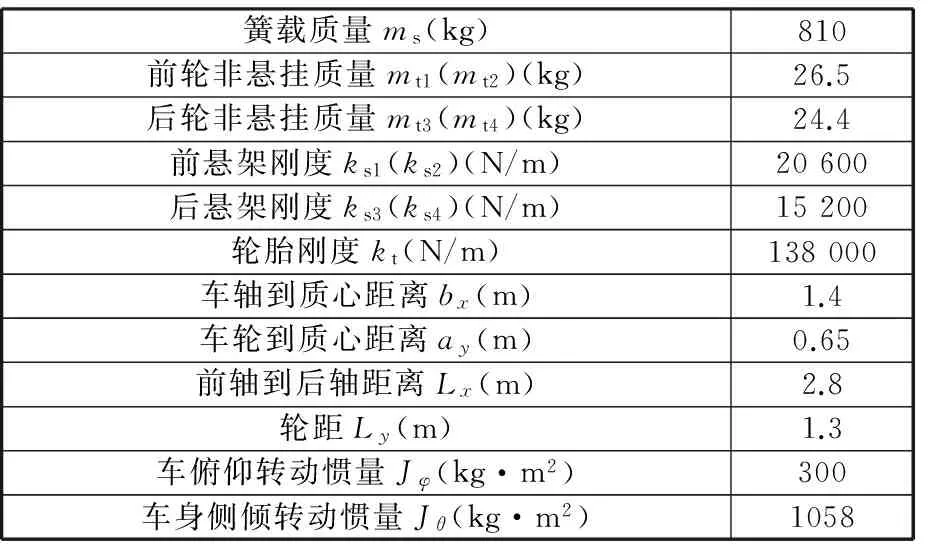
表1 车型主要参数表Tab.1 Major parameters of vehicle

表2 鱼群算法参数设置Tab.2 Parameter of artificial fish swarmoptimization algorithm

将基于鱼群-最优控制算法(AF-LQG)的永磁体-电磁阀式磁流变阻尼器整车半主动悬架系统仿真结果与单独永磁体磁流变阻尼器整车被动(PASSIVE)悬架系统仿真结果进行比较，结果如图8～图12所示，同时，为了更加精确地对仿真结果进行分析，计算了各仿真结果均方根值和方差，见表3。

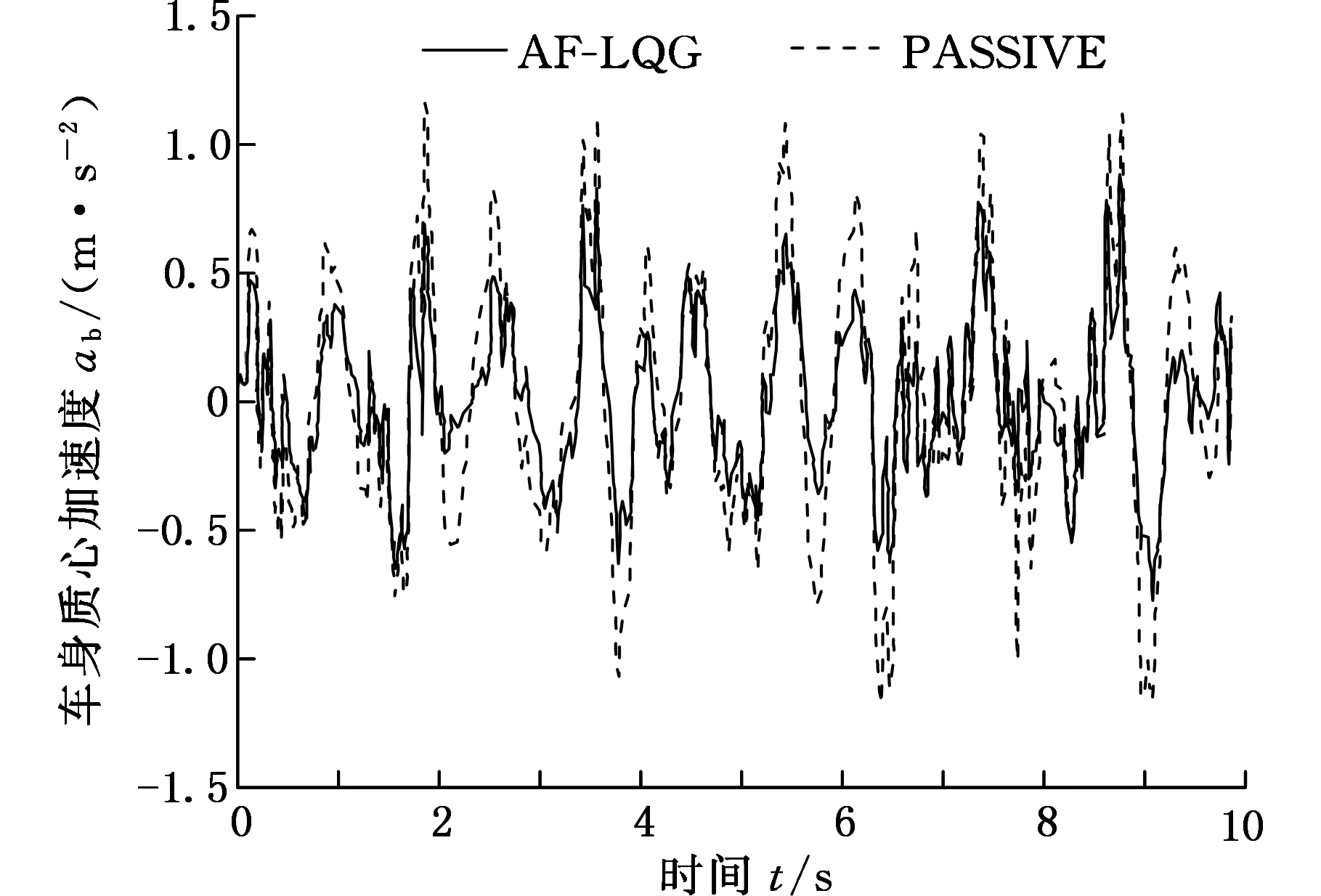
图8 车身质心加速度曲线Fig.8 Curve of vertical acceleration of center of vehicle body

图9 俯仰角加速度曲线Fig.9 Curve of pitch angular acceleration

图10 侧倾角加速度曲线Fig.10 Curve of roll angular acceleration

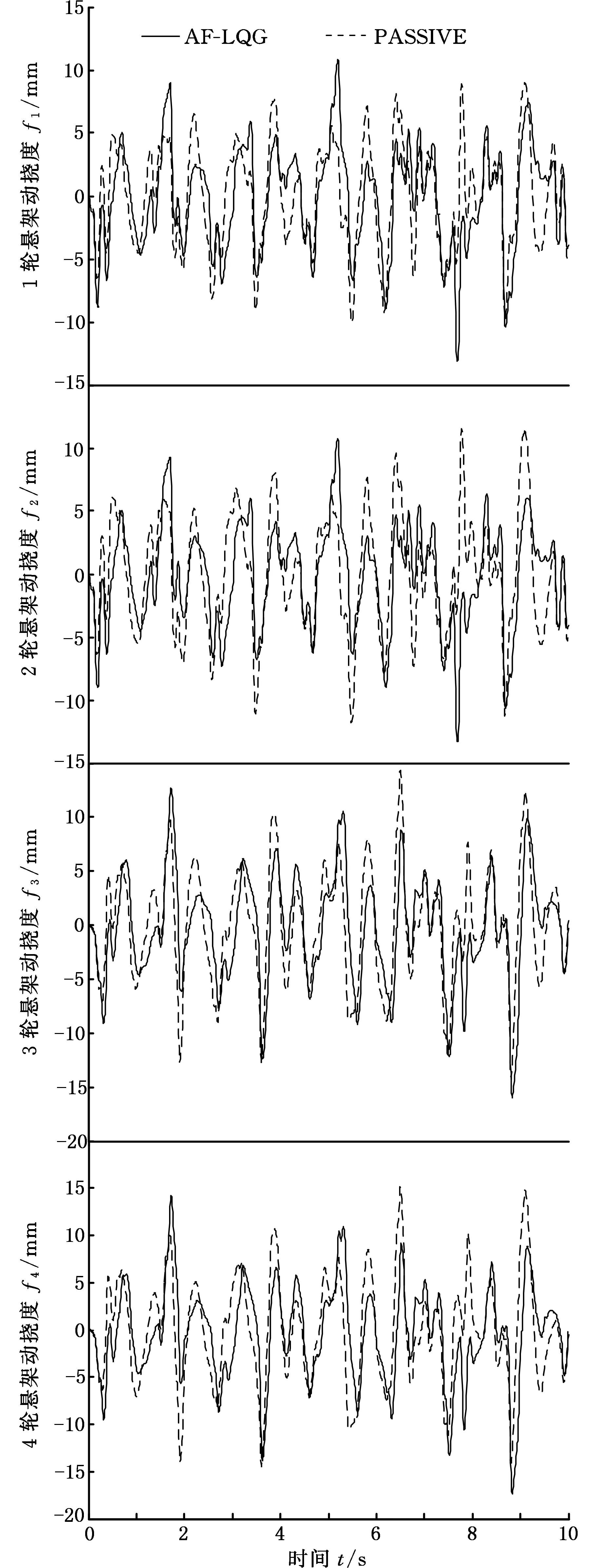
图11 悬架动挠度曲线Fig.11 Curve of suspension dynamic deflection

由图7～图10和表3可以看出，相比被动悬架汽车，基于鱼群最优控制算法控制的汽车质心垂直加速度、俯仰角加速度、车身侧倾角加速度分别提高了38.95%、35.12%、35.98%；这说明鱼群最优控制算法悬架系统可以更好地消减车身振动、车身侧倾角、俯仰角，提高汽车的平顺性和行驶安全性；同时也可以看出，永磁体-电磁阀磁流变阻尼器悬架性能比单独内置永磁体的被动悬架性能优良。由图11、图12和表3可以看出，基于鱼群最优控制算法的汽车4个车轮处的悬架动挠度、动位移较单独内置永磁体流变阻尼器悬架4个车轮处的动挠度、动位移分别减小了0.1521%、12.08%，6.162%、10.65%，19.58%、26.05%，20.09%、26.73%；这也说明基于鱼群最优控制算法控制的悬架可以提高汽车的平顺性，永磁体-电磁阀式磁流变阻尼器悬架比单独内置永磁体磁流变阻尼器悬架性能优良。

6 结论

(1)本文设计了汽车悬架使用的永磁体-电磁阀式磁流变阻尼器，并建立了仿真模型；示功特性试验结果表明，所设计的新型阻尼器可以满足汽车悬架的使用要求，同时，速度特性试验结果表明，所建立的阻尼器模型具有较高的可信度。

(2)基于牛顿定律建立了7自由度整车悬架模型；为了提高悬架控制效果，在对常规鱼群算法进行改进的基础上设计了适合于汽车悬架系统的鱼群最优控制算法实现了两者的集成控制。

(3)仿真试验结果表明，鱼群-最优控制控制不仅可以提高汽车的平顺性，而且可以提高操纵稳定性，进一步提高汽车的动力学性能、行驶安全性、乘坐舒适性。

[1] 邹得和. 德尔福的新一代MagneRide磁流变阻尼可调减振器[J]. 汽车与配件,2008(20):34-35.

ZOU Dehe.Delphi New Magneto-rheological Damping Adjustable Shock Absorber[J]. Auto Technology & Market,2008(20):34-35.

[3] 董小闵, 于建强, 杨茂举,等. 考虑温度因素的磁流变减振器的优化设计与实验[J]. 振动与冲击，2016,35(8)：54-59.

DONG Xiaomin, YU Jianqiang, YANG Maoju, et al. Optimization and Experimental Study of Magnetorheologieal Fluid Damper Considering Temperature Effects[J].Journal of Vibration and Shock,2016,35(8)：54-59.

[4] BOESE H, EHRLICH J. Performance of Magnetorheological Fluids in a Novel Damper with Excellent Fail-safe Behavior[J]. Journal of Intelligent Material Systems and Structures,2010,21(15):1537-1542.

[5] 唐欣, 凌虹, 胡克鳌. 磁流变液沉降稳定性研究现状与趋势[J]. 磁性材料及器件,2004,35(3):5-8.

TANG Xin, LING Hong, HU Keao. Current Status and Future Trends of Research in Subsidence Stability of Magnetorheological Fluids[J].Journal of Magnetic Materials and Devices,2004,35(3):5-8.

[6] TOPÇU O, AYGÜN M M, ÖZGÜR ÇÖLLÜ,et al. Experimental Investigation of a Magnetorheological Fluid Damper with Permanent Magnet for Haptic Finger Grasping[C]//The Int. Conf. on Mechatronics and Machine Vision in Practice. Berlin,2013:105-112.

[7] BÖSE H, EHRLICH J. Magnetorheological Dampers with Various Designs of Hybrid Magnetic Circuits[J]. Journal of Intelligent Material Systems and Structures,2012,23(9):979-987.

[8] BÖSE H,EHRLICH J.Performance of Magnetorheological Fluids in a Novel Damper with Excellent Fail-safe Behavior[J].Journal of Intelligent Material Systems and Structures,2010,21(15):1537-1542.

[9] CHOI Y T, WERELEY N M. Self-Powered Magnetorheological Dampers [J]. Journal of Vibration and Acoustics,2009,131(4):1-5.

[10] YAN Weiming, JI Jinbao, DONG Bin,et al. Theoretical and Experimental Studies on a New Reversible Magnetorheological Damper [J].Structural Control & Health Monitoring,2011,18(1):1-19.

[11] XIAO P, WANG Q, NIU L, et al. Research on Suspension System with Embedded-permanent-magnet Magnetorheological Damper Based on V-model[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,2016,230(10):1602-1614.

[12] YANG G, SPENCER B F, CARLSON JD, et al. Large-scale MR Fluid Dampers: Modeling and Dynamic Performance Considerations[J]. Engineering Structures,2002,24(3):309-323.

[13] 吴莹, 李佳佳, 农多敏,等. 减速带激励下汽车的非线性振动特性分析[J]. 动力学与控制学报,2014(2):147-152.

WU Ying, LI Jiajia, NONG Duomin, et al. Nonlinear Vibration Analysis for Automobile Stimulated by Speed Control Hump[J]. Journal of Dynamics and Control,2014(2):147-152.

[14] 刘伟, 刘大维, 陈焕明,等. 基于联合仿真的半主动悬架车辆行驶平顺性研究[J]. 农业机械学报,2009,40(6):16-22.

LIU Wei, LIU Dawei, CHEN Huanmin, et al. Ride Comfort of MR-damper Semi-active Suspension Systems Based on Co-simulations[J]. Transactions of the Chinese Society for Agricultural Machinery,2009,40(6):16-22.

Semi-activeSuspensionSystemwithNovelPermanentMagnet-solenoidValveTypeMRDamperbyArtificialFishSwarmOptimizationAlgorithm

HU Hongsheng1XIAO Ping2JIANG Ming2OUYANG Qing1

1.College of Mechanical and Electrical Engineering, Jiaxing University, Jiaxing,Zhejiang,314001 2.School of Mechanical and Automotive, Anhui Polytechnic University, Wuhu, Anhui,230031

A semi-active suspension control system with MR damper was studied in order to improve the performances of automobile suspension systems. Firstly, a new type of MR damper with permanent magnet and solenoid valve structure configuration was designed according to the MR fluid theory. The theoretical dynamics model of MR damper was established and verified with high credibility byF-vexperimental curves. In addition, theF-Sindicator diagrams of damper show that it may satisfy the operating requirements of vehicle suspensions. Secondly, a 7-DOF mathematical vibration model of vehicle suspensions was set up according to the principles of vehicle system dynamics. The LQG controller using the improved artificial fish swarm algorithm was proposed to reduce the structural responses in the vehicle suspension system. Finally, the simulation experiments of vehicle suspension systems were carried out. Compared to the passive systems, the semi-active suspension systems based on the artificial fish swarm algorithm may be significantly improve the vehicle dynamics performance, where the vehicle body centroid vertical acceleration, pitching angular acceleration and vehicle roll angle are decreased by 38.95%、35.12%、35.98% respectively.

magnetorheological (MR) damper; permanent magnet; solenoid valve; semi-active suspension; artificial fish swarm algorithm;

TP39

10.3969/j.issn.1004-132X.2017.21.002

2016-12-15

国家自然科学基金资助项目(51575001；浙江省公益性技术项目(2016C31051)；安徽省高校自然科学研究重点项目(KJ2016A799)；嘉兴市科技计划重点工业项目(2016AY13003)

(编辑陈勇)

胡红生，男，1976年生。嘉兴学院机电工程学院教授。主要研究方向为振动噪声控制、汽车零部件关键技术等。E-mail:wjhhs@126.com。肖平，男，1973年生。安徽工程大学机械与汽车工程学院副教授。江明，男，1991年生。安徽工程大学机械与汽车工程学院硕士研究生。欧阳青，男，1987年生。嘉兴学院机电工程学院讲师。