基于改进自适应杂交粒子群优化算法和最小二乘支持向量机的空中目标威胁评估

许凌凯，杨任农，左家亮

(空军工程大学 航空航天工程学院，西安 710038)(*通信作者电子邮箱xulin395@163.com)

基于改进自适应杂交粒子群优化算法和最小二乘支持向量机的空中目标威胁评估

许凌凯*，杨任农，左家亮

(空军工程大学 航空航天工程学院，西安 710038)(*通信作者电子邮箱xulin395@163.com)

评估空中目标威胁程度是防空指挥控制系统的核心环节，评估的准确程度将对防空作战产生重大影响。针对传统评估方法实时性差、工作量大、评估精度不足、无法同时进行多目标评估等缺陷，提出了一种基于自适应杂交粒子群优化(ACPSO)算法和最小二乘支持向量机(LSSVM)的空中目标威胁评估方法。首先，根据空中目标态势信息构建威胁评估系统框架；然后，采用ACPSO算法对LSSVM中的正则化参数和核函数参数进行寻优，针对传统杂交机制的不足提出改进的交叉杂交方式，并使杂交概率自适应调整；最后，对比分析了各系统的训练和评估效果，并用优化后的系统实现多目标实时动态威胁评估。仿真结果表明，所提方法评估精度高，所需时间短，可同时进行多目标评估，为空中目标威胁评估提供了一种有效的解决方法。

威胁评估;防空作战;自适应杂交粒子群优化;最小二乘支持向量机

0 引言

在信息化战争中，防空作战是以电子信息系统为平台，在陆、海、空、天、电磁等多维空间以及全方位、全空域、全天候、全天时战场环境下全面展开的战争形态[1-2]。空中目标会对我方防空力量构成严重威胁，空中目标威胁程度是指空中目标在没有遭受我方防空武器拦截和对抗条件下，对我方防空区域内的目标进行攻击的可能性和成功攻击后可能造成的毁伤程度[3]。对空中目标威胁程度进行评估是防空指挥控制系统的关键，也是各级进行目标分配和火力分配的基本依据[4]。

目前在空中目标威胁评估的研究中，评估方法大致分为传统的专家评估法和人工智能评估法，其中专家评估法是由专家通过雷达获取的数据，分析当前空中目标的态势信息，根据专家经验给出一个合理的目标威胁等级，虽然专业性强，但战场态势瞬息万变，只通过专家分析的方法不仅实时性差而且工作量大，且当空中存在多个威胁目标时，专家往往无法同时评估多个目标。人工智能评估法主要有BP神经网络法和支持向量机方法等，文献[5-6]采用神经网络法对目标威胁进行评估，但是神经网络理论存在网络结构复杂、训练时间长、鲁棒性差、模型预测精度低等问题。文献[7-8]采用标准型支持向量机，取得精度较高的评估结果，但该方法需要解决二次规划问题，模型较为复杂，训练时间长。最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)是标准支持向量机的改进和扩展，将二次规划问题转换为线性方程组求解问题，使计算复杂性大幅度降低，故本文选取LSSVM作为基本模型。

在LSSVM模型中，正则化参数和核函数参数直接影响模型的评估精度，如何寻得最优参数是技术难点，文献[9]采用经典粒子群算法对模型参数进行寻优，该算法容易陷入局部极值出现早熟收敛现象，文献[10]对粒子群算法中的惯性因子进行研究，得出自适应调整的混沌惯性因子具有最佳的平均精度，可提高粒子群全局搜索能力。文献[11]研究了一种杂交粒子群算法，通过杂交机制可有效提高种群多样性，但该算法在实际应用过程中存在杂交方式不合理、种群在迭代后期局部搜索能力不足等问题。

基于上述研究存在的问题，本文提出一种优化的人工智能算法来构建空中目标威胁评估系统。首先从客观数据中提取出目标的态势信息，结合专家评判获得目标的威胁等级并构建“态势信息-威胁等级”样本库，然后利用样本库对LSSVM进行训练，采用自适应杂交粒子群优化(Adaptive Crossbreeding Particle Swarm Optimization, ACPSO)算法对参数进行寻优，针对传统杂交机制的不足提出改进的杂交机制，最后运用已优化的系统对样本进行评估。实验结果表明了所提方法的优越性和实用性。

1 空中目标威胁评估系统原理

1.1 空中目标态势信息

空中目标的态势信息是威胁评估所需的直接参数，在目标入侵我方防空区域时，我方雷达与目标的位置关系如图1所示。其中，Ri为我方雷达，Bj为敌方飞机，hij为目标高度，dij为我方雷达与目标之间的距离，vj为目标的速度矢量，aij为目标方位角，βij为目标进入角。

图1 相对位置关系

除了位置关系外，目标的雷达截面积(Radar Cross Section, RCS)也是态势信息的重要参数。RCS越小，雷达对目标的信号特征就越小，探测距离也越短，从而目标对我方威胁程度越大。空中目标态势信息参数描述见表1。

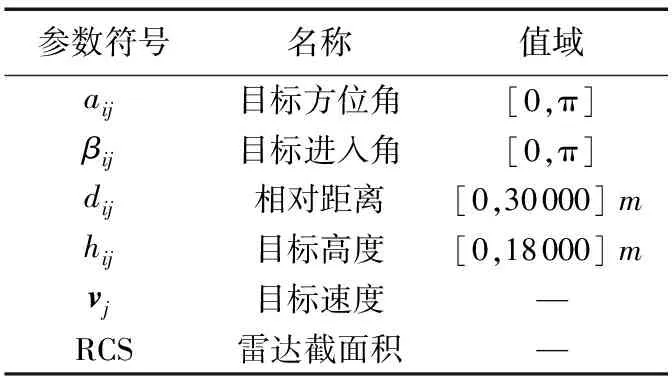
表1 态势信息参数描述

1.2 空中目标威胁评估系统框架

从雷达采集的数据中提取出若干组目标的态势信息，结合专家评判对每组态势信息进行威胁等级分类(威胁程度高、中、低)，以此来构建“态势信息-威胁等级”样本库，利用样本库训练LSSVM模型，其中如何寻找LSSVM最优参数是影响优化评估的难点，本文使用改进的ACPSO算法对模型进行优化，从而得到改进ACPSO-LSSVM威胁评估系统，系统框架如图2所示。

图2 空中目标威胁评估系统框架

2 空中目标威胁评估算法

2.1 最小二乘支持向量机

最小二乘支持向量机(LSSVM)的基本思想是将最小二乘引入传统支持向量机中，使最小二乘中的线性系统代替传统支持向量机中的二次规划方法[12]。LSSVM不仅有效降低了计算的复杂度，其采用的结构风险最小化原则很好地保证了预测结果的准确性。

设训练样本集表示为(xi,yi)，其中xi为输入向量，yi是分类标签，求解样本集的最优化问题可描述如下：

(1)

s.t.yi=φ(xi)×ω+b+ξi;i=1,2,…,n

其中：φ(xi)为原空间到核空间的映射函数，ω为核空间权矢量，ξi≥0为松弛变量，b为根据训练样本确定的偏置，γ为正则化参数。通过引入Lagrange法来求解这个优化问题：

(2)

最终可得出LSSVM的最优分类函数：

y(x)=sign[∑aiyiK(x,xi)+b];i=1,2,…,n

(3)

其中:sign()是符号函数，n为训练样本数，xi为训练样本，x为待预测样本，b为根据训练样本确定的偏置，K(x,xi)为核函数，一般选取径向基函数作为核函数。

2.2 改进的自适应杂交粒子群算法

2.2.1 经典粒子群算法

经典粒子群优化(Particle Swarm Optimization, PSO)算法属于一种全局随机寻优算法，其基本原理是：设在m维空间中包含n个粒子的种群，每个粒子都代表优化问题的一个可能解，将粒子的位置代入目标函数进行计算可得到粒子当前的适应度。粒子在搜索空间中的飞行速度会受到自身以及群体的飞行经验的影响进行动态调整，并以此不断更新自身位置直到达到最优解。在每一次迭代过程中，粒子都会通过计算其个体极值和全局极值的方式来对位置和速度进行相应的更新，更新公式为：

(4)

(5)

2.2.2 惯性因子自适应调整

在PSO算法中，惯性因子w是影响粒子收敛速度和收索精度的重要参数，由于混沌运动具有随机性、规律性、遍历性等特征，Feng等[13]提出了一种基于混沌优化机制的惯性权重调整方法，文献[10]对比了15种惯性权重的调整方法，结果表明混沌惯性权重具有最佳的平均精度，故本文选择混沌惯性权重调整方法来更新式(4)中的惯性因子w，更新公式[14]如下：

w(t)=(wmax-wmin)(DM-Dt)/DM+wmin×z

(6)

z=4×rand×(1-rand)

(7)

其中：rand为分布于[0,1]的随机数,wmax与wmin分别表示惯性因子w在迭代开始和结束时的取值，DM为最大迭代次数，Dt为当前迭代次数。

2.2.3 引入杂交算法

PSO算法最大的缺陷是粒子容易陷入局部最优而出现早熟收敛现象，早熟收敛会使种群丧失活性，降低种群的多样性，从而影响算法的精度。Løvbjerg等[15]将遗传算法中的复制和重组这些称为杂交的操作引入到粒子群算法中，在迭代过程中，根据杂交概率Pc选取指定数量的粒子为父代粒子，父代粒子两两杂交生成子代粒子，新生成的子代粒子不断代替父代粒子，从而使陷入局部最优的粒子跳出来。子代粒子的位置和速度更新公式如下：

(8)

其中：child(x)与child(v)分别代表子代粒子的位置与速度，parent(x)与parent(v)分别代表父代粒子的位置与速度，Pc为[0,1]的随机数。当两个陷入不同局部最优的粒子进行杂交操作后，往往能从局部最优处逃脱，因此引入杂交算法能增强种群的全局寻优能力。

2.2.4 杂交机制的改进

传统的杂交方式为两两随机组合进行杂交，这种杂交方式存在一个问题：若两个收敛于同一局部最优的粒子与粒子进行杂交，则产生的后代粒子与依然会在该局部最优内，导致杂交性能降低，对此，提出一种交叉杂交的方式，如图3所示，将参加杂交的粒子按适应度从小到大排序，假设有2k个粒子参加杂交，则第1个粒子与第k+1个粒子杂交，第2个粒子与第k+2个粒子进行杂交，以此类推。

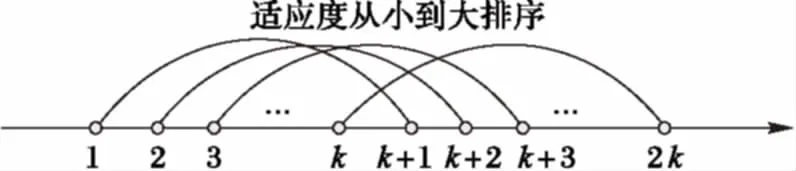
图3 粒子的交叉杂交方式

另一方面，粒子在进化过程，杂交概率Pc为固定值，这就导致迭代后期较大的杂交概率会使种群难以在局部范围内进行精确挖掘，从而导致算法精度降低。针对该缺陷进行改进，加入杂交控制因子，使杂交概率随着迭代次数增加线性降低：

σ=(DM-Di)/DM

(9)

其中：Di为当前迭代次数，DM为最大迭代次数。引入杂交控制因子后，粒子群的杂交概率由固定值Pc变为自适应调整的σPc，既保证了迭代初期种群的多样性，又避免了粒子在迭代后期局部搜索能力的降低。

2.3 算法流程

利用改进ACPSO算法优化LSSVM的流程如图4所示。

图4 ACPSO优化LSSVM流程

3 实验分析

3.1 数据处理

以雷达采集的数据进行实例研究，从“态势信息-威胁等级”样本库中选取三组不同数据，每组数据各以500例作为训练样本，50例作为测试样本，且无重复样本。

将目标的态势信息作为输入，威胁等级作为分类标签，放入系统中进行训练。为消除不同量纲对实验结果的影响，需利用式(10)对目标的态势信息进行归一化处理：

(10)

3.2 系统训练

基于Matlab环境，运用LSSVM工具箱编写相关算法程序，设定改进ACPSO算法的进化代数为300，种群大小为30，初始杂交概率Pc设为0.5，杂交粒子数量设为10，加速因子c1、c2均设为1.496 18，正则化参数的搜索空间为0.01～100，核函数参数的搜索空间为0.01～1 000，核函数选择径向基核函数。其中，进化代数300次作为算法的终止条件，种群大小一般设置为20或30，初始杂交概率一般设为0.5，杂交粒子数量一般占种群数量的三分之一，加速因子c1、c2均设为1.496 18时有利于算法的收敛，适应度函数为LSSVM工具箱中的lssvmtrain函数，并结合5折交叉验证，以交叉验证所得到的正确率作为算法的适应度值。训练过程中每组数据的适应度变化曲线如图5所示。

由图5可知，随着迭代次数不断增加，种群最佳适应度呈阶梯状增长。第一组数据中，当迭代进行到275次时，适应度达到最大，为0.92；第二组数据中，当迭代进行到276次时，适应度达到最大，为0.91；第三组数据中，当迭代进行到281次时，适应度达到最大，为0.89。由此可知，算法对三组数据分别进行训练时，均能达到较高的适应度水平，其中对第一组数据的训练效果最好。

图5 三组数据的适应度变化曲线

在每组数据中，找到最大适应度的粒子所对应的惯性因子变化曲线如图6所示。

图6 三组数据的惯性因子变化曲线

由图6可知，每组数据中，惯性因子的变化均满足混沌特性，整体趋势随着迭代的进行非线性降低。

为验证算法的可信性和优越性，作如下对比研究：

分别用改进ACPSO算法、ACPSO算法和经典PSO算法对第一组数据中的参数进行寻优，适应度变化曲线对应图7中的粗实线、细实线和虚线。

图7 三种算法的适应度变化曲线

分析可知：经典PSO算法适应度更新次数最少，表示其种群多样性较差，在迭代进行到90次左右时，适应度不再变化，表示算法陷入局部最优，出现早熟收敛现象；而ACPSO算法由于引入杂交机制，跳出局部最优，适应度继续更新。由此可见，ACPSO算法的全局寻优能力强于经典PSO算法。改进ACPSO算法比未改进ACPSO算法的优化之处在于迭代后期，由于改进了杂交机制，杂交效率得到提高，同时粒子在迭代后期杂交概率不断降低，使得种群更加专注于局部搜索，提高了迭代后期算法的搜索精度。此时算法找到的最优γ和值分别为22.376 2和125.846 1。

将经典PSO算法和改进ACPSO算法的种群位置分布进行比较，如图8所示，以第一组数据为例，每一个小圆圈代表种群中某个粒子曾经到达过的位置，γ表示正则化参数，g表示核函数参数。

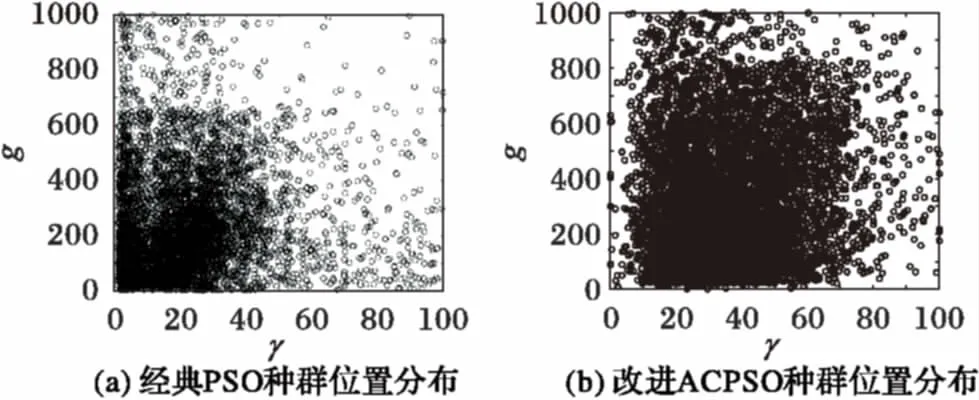
图8 种群位置分布对比

由图8可知，经典PSO算法的种群分布较为集中，原因是种群的运动容易受到最优粒子的影响，易陷入局部最优。改进ACPSO算法的粒子通过杂交机制增加了种群多样性，种群分布较为分散，不易陷入局部最优，其全局寻优能力强于经典PSO算法。

3.3 系统评估

分别采用改进ACPSO算法、ACPSO算法、BP神经网络法、经典PSO算法、网格法，结合LSSVM构建的评估系统对数据进行评估。其中，BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络，具有很强的非线性映射能力和自适应能力。网格法是将整个搜索空间以网格的形式进行划分，网格上的每一个点代表算法的一个解，通过遍历网格上所有的点来寻得算法最优解。

以第一组数据为例，评估结果对比如图9所示。

图9 不同系统评估结果对比

从图9中可知，改进ACPSO-LSSVM评估系统的训练集拟合度以及测试集评估精度均最高，分别为95.4%和92%，比未改进ACPSO系统分别提高了2.8%与4%，比经典PSO系统分别高出12.6%与14%。BP神经网络系统处于中间水平，而网格法系统效果最差，原因是网格法在整个数据空间进行搜索，搜索空间和搜索间隔比较大，而智能搜索算法能明显减小搜索空间，提高搜索效率。

将不同系统的训练时间和评估时间进行对比，如表2所示。

表2 系统消耗时间对比

其中，训练时间是指系统对三组数据进行训练时，每组数据的平均训练时间，评估时间是指系统对单个样本进行评估时所需平均时间。

由表2可知，LSSVM的训练时间最短，比SVM有较大的提高，BP神经网络训练时间最长。在对目标进行威胁评估时，三种系统消耗时间均很短，表明采用人工智能评估法能很好满足实时性的要求。

3.4 多目标实时动态威胁评估

设某一时刻，我方雷达搜索到防空区域内出现目标A与目标B，并对其进行实时观测，每隔10 s将目标的态势信息输送到评估系统，评估系统对态势进行分析并将评估结果动态显示出来，如图10所示。

图10中的实线部分模拟的是目标A的实时动态威胁评估，目标A的运动方式为直线穿过我方防空区域，当目标A被我方雷达侦测到时，威胁等级为低，随着目标不断深入，威胁等级不断提高，当目标穿过防空区后，威胁等级随着目标A的离开而降低。虚线部分模拟的是目标B的实时动态威胁评估，目标B的运动方式为先进入我方防空区，然后在防空区上空盘旋，最后离开防空区，对应于曲线中的威胁等级由低变高，然后在中与高之间交替变化，最后随着目标的离开威胁程度降为低。

图10 多目标实时动态威胁评估

4 结语

本文提出了一种基于改进ACPSO算法和LSSVM的空中目标威胁评估方法。首先根据目标的态势信息构建威胁评估系统框架，然后利用ACPSO算法对LSSVM模型进行优化，针对ACPSO算法中杂交机制的不足，提出了改进的杂交机制，最后对所提方法的有效性和优越性作了对比研究。仿真结果表明，所提方法可有效评估当前目标的威胁等级，评估精度高、速度快，可进行多目标实时动态威胁评估，具有一定的参考价值。

References)

[1] MORELLAS V, PAVLIDIS I, TSIAMYRTZIS P. DETER: detection of evens for threat evaluation and recognition [J]. Machine Vision and Applications, 2003, 15(1): 29-45.

[2] 张旭东，彭杰，纪军.基于熵的逼近于理想解的排序法空袭目标威胁度评估[J].计算机应用，2011,31(11):3140-3142.(ZHANG X D, PENG J, JI J. Air-raid target threat degree evaluation based on entropy TOPSIS method [J]. Journal of Computer Applications, 2011, 31(11): 3140-3142.)

[3] 张肃.空中目标威胁评估技术[J].情报指挥控制系统与仿真技术,2005,27(1):41-45.(ZHANG S. Evaluation technology of the aerial targets’ threat [J]. Information Command Control System & Simulation Technology, 2005, 27(1): 41-45.)

[4] 马其东，方立恭.海上区域防空目标威胁评估模型[J].现代防御技术,2009,37(1):15-19.(MA Q D, FANG L G. Research on threat assessment model of air target for area air defense [J]. Modern Defence Technology, 2009, 37(1): 15-19.)

[5] 胡起伟，石全，王广彦，等.基于神经网络的威胁评估研究[J].计算机仿真，2006,23(6):25-27.(HU Q W, SHI Q, WANG G Y, et al. Threat assessment based on neural network [J]. Computer Simulation, 2006, 23(6): 25-27.)

[6] 张发强，由大德，蒋敏.基于RBF神经网络的空袭目标威胁评估模型研究[J].舰船电子对抗，2010,33(6):85-88.(ZHANG F Q, YOU D D, JIANG M. Study of the threat assessment model for air raid targets based on RBF neural network [J]. Shipboard Electronic Countermeasure, 2010, 33(6): 85-88.)

[7] 郭辉，徐浩军，刘凌. 基于回归型支持向量机的空战目标威胁评估[J].北京航空航天大学学报，2010，36(1):123-126.(GUO H, XU H J, LIU L. Target threat assessment of air combat based on support vector machines for regression [J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(1): 123-126.)[8] 郭辉，吕英军，王平，等.基于区间支持向量回归的空战目标威胁评估[J].火力与指挥控制，2014,39(8):17-21.(GUO H, LYU Y J, WANG P, et al. Target threat assessment of air combat based on intervals and SVR [J]. Fire Control & Command Control, 2014, 39(8): 17-21.)

[9] 谷文成，柴宝仁，滕艳平.基于粒子群优化算法的支持向量机研究[J].北京理工大学学报，2014,34(7):705-709.(GU W C, CHAI B R, TENG Y P. Research on support vector machine based on particle swarm optimization [J]. Transactions of Beijing Institute of Technology, 2014, 34(7): 705-709.)

[10] BANSAL J C, SINGH P K, SARASWAT M, et al. Inertia weight strategies in particle swarm optimization [C]// Proceedings of the 2011 3rd World Congress on Nature and Biologically Inspired Computing. Piscataway, NJ: IEEE, 2011: 633-469.

[11] 王江荣，文晖，任泰明.基于杂交粒子群算法的多元线性回归参数估计及预测区间研究[J].水泥工程，2014(5):6-9.(WANG J R, WEN H, REN T M. Multiple linear regression parameters estimation and prediction intervals research based on hybrid particle swarm optimization [J]. Cement Engineering, 2014(5): 6-9.)

[12] SUYKENS J A K, LUKAS L, VANDEWALLE J. Sparse least squares support vecter machines for adaptive communication channel equalization [J]. International Journal of Applied Science and Engineering, 2005, 11(3): 51-59.

[13] FENG Y, TENG G F, WANG A X, et al. Chaotic inertia weight in particle swarm optimization [C]// Proceedings of the 2007 2nd International Conference on Innovative Computing, Information and Control. Piscataway, NJ: IEEE, 2007: 475-476.

[14] 李蓉，沈云波，刘坚.改进的自适应粒子群优化算法[J].计算机工程与应用,2015,51(13):31-36.(LI R, SHEN Y B, LIU J. Improved adaptive particle swarm optimization algorithm [J]. Computer Engineering and Applications, 2015, 51(13): 31-36.)

[15] LØVBJERG M, RASMUSSEN T K, KRINK T. Hybrid particle swarm optimiser with breeding and subpopulations [C]// Proceedings of International Conference on Genetic and Evolutionary Computation Conference.San Francisco：Morgan Kaufmann，2001: 101-106.

AirtargetthreatassessmentbasedonimprovedACPSOalgorithmandLSSVM

XU Lingkai*, YANG Rennong, ZUO Jialiang

(CollegeofAeronauticsandAstronauticsEngineering,AirForceEngineeringUniversity,Xi’anShaanxi710038,China)

The key link of air defense command and control system is to evaluate the threat degree of air target according to target situation information, the accuracy of the assessment will have a significant impact on air defense operations. Aiming at the shortcomings of traditional evaluation methods, such as poor real-time performance, heavy workload, low evaluation accuracy, and unable to evaluate multiple objectives simultaneously, a method of air target threat assessment based on Adaptive Crossbreeding Particle Swarm Optimization (ACPSO) and Least Squares Support Vector Machine (LSSVM) was proposed. Firstly, according to the air target situation information, the framework of threat assessment system was constructed. Then, ACPSO algorithm was used to optimize the regularization parameter and kernel function parameter in LSSVM. In order to overcome the disadvantages of the traditional crossbreeding mechanism, an improved cross-hybridization mechanism was proposed, and the crossbreeding probability was adjusted adaptively. Finally, the training and evaluation results of the systems were compared and analyzed, and the multi-target real-time dynamic threat assessment was realized by the optimized system. Simulation results show that the proposed method has the advantages of high accuracy and short time required, and can be used to evaluate multiple targets simultaneously. It provides an effective solution to evaluate the threat of air targets.

threat assessment; air defense operation; Adaptive Crossbreeding Particle Swarm Optimization (ACPSO); Least Squares Support Vector Machine (LSSVM)

2017- 04- 06;

2017- 06- 07。

国家杰出青年科学基金资助项目(71501184)。

许凌凯(1993—),男,湖北鄂州人，硕士研究生，主要研究方向：机器学习与智能空战； 杨任农(1968—),男,四川彭州人，教授，博士，主要研究方向：航空兵任务规划与作战效能评估； 左家亮(1987—),男, 陕西西安人，博士，主要研究方向：航空兵任务规划与作战效能评估。

1001- 9081(2017)09- 2712- 05

10.11772/j.issn.1001- 9081.2017.09.2712

TP181

A

This work is partially supported by the National Science Fund for Distinguished Young Scholars (71501184).

XULingkai, born in 1993, M. S. candidate. His research interests include machine learning and intelligent air combat.

YANGRennong, born in 1968, Ph. D., professor. His research interests include mission planning and operational effectiveness evaluation of air force.

ZUOJialiang, born in 1987, Ph. D. His research interests include mission planning and operational effectiveness evaluation of air force.