流量抑制模型研究及其回归分析
2017-11-14韩明彭宣孙克雄陈明
韩明+彭宣+孙克雄+陈明

【摘 要】为满足用户4G数据业务需求,预警数据业务流失,研究了4G数据业务中的流量抑制现象及其影响因素,选取页面显示时长作为流量抑制现象的表征指标,并建立了预测分析模型,应用相关性和回归分析方法研究无线网络各因素的影响程度。结果表明,建立的多元线性回归模型对页面显示时长的解释有效,上下行覆盖的信号强度和质量以及小区负荷因素对影响页面显示时长有重要影响。
【关键词】LTE 流量抑制 页面显示时长 线性回归
中图分类号:TN929.5 文献标志码:A 文章编号:1006-1010(2017)19-0015-06
Research on Data Traffic Suppression Model Using Linear Regression
HAN Ming1, PENG Xuan2, SUN Kexiong1, CHEN Ming3
[Abstract] In order to meet the users requirement of 4G data traffic and warn the loss of data traffic, the traffic suppression and influencing factors in 4G data service were investigated. The page display duration is used as the indicator of traffic suppression. The prediction and analysis model was built. The correlation and linear regression analysis method were used to study the impact of different wireless network factors. Results demonstrate the multiple linear regression model can effectively interpret the page display duration. Besides, both the uplink and downlink signal strength and quality and the cell load have the significant impact on the page display duration.
[Key words]LTE traffic suppression page display duration linear regression
1 引言
随着4G LTE技术发展以及运营商对终端用户消费习惯的引领,移动数据业务收入占比越来越高,据2016年底统计,无线数据业务已成中国移动第一大收入来源[1],其运营情况越来越得到重视。但在实际的无线数据运营过程中,由于多种原因的影响,部分数据业务不能得到及时有效的释放,会造成资源承载效率降低、数据业务流失、客户感知下降等问题。
为了充分释放用户数据业务需求,预警数据业务的流失,本文提出流量抑制的概念并选取了其表征指标,建立了基于网络KPI的多元线性回归模型。线性回归作为一种回归预测方法在各行各业有着广泛的应用,可将定性问题定量化,确定各特征对结果的影响程度,用于指导工作实践。
2 流量抑制及模型构建
2.1 流量抑制现象的产生
在无线数据业务中,由于各种网络原因导致部分数据业务不能及时有效地释放,造成数据业务流失及用户体验降低的情况称为流量抑制。比如下载速率低而导致用户页面浏览减少,或者是音质差画面卡顿等因素导致用户放弃使用即时通信、视频浏览等。
根据LTE用户数据业务模型统计,基于HTTP协议的Web业务类型占据主导地位[2]。在假设用户数据业务模型一致的情况下,小区流量会随着用户数增加而线性增长,公式如下:
数;a为单用户数据量,受用户模型影响;统计时长一般为1小时。
实际小区流量由于受各种网络因素影响,不能满足以上线性关系,当用户数增加时出现流量增长缓慢甚至下降的情况,如图1所示,比如用户数超出小区限制后,潜在用户不能有效接入小区导致业务流失,流失业务量即为流量抑制的损失量。流量损失公式表示如下:
LTE RRU小区并发用户数增加会对多个网络KPI、用户感知、小区流量等指标产生影响[3]。根据实际网络性能统计,当小区用户数低于200时,小区流量基本线性增长;超过200时小区流量增长变缓,甚至有下降的可能,如受故障、覆盖、干扰等因素影响时。
2.2 流量抑制的表征指标选取
单用户页面浏览一般是脉冲式突发行為,如图2所示。对于单个用户的流量损失,假设一个用户在t1~t6时间内正常情况下有4次页面请求,柱体宽度标示平均页面显示时长t≈2.5 s[4]。t2时刻页面显示正常,t3时刻由于网络因素影响,页面显示时长增加?t而延长到t4时刻,原来t4/t5时刻的流量需求就会顺序后延,原t5时刻的流量需求延迟到统计时间T(t1~t6期间)之外或直接放弃,则在统计时间内由于流量抑制而导致的流量损失量ΔLoss=0.7 MB。
用户突发式页面请求的业务量可以转换为连续值近似代替,假设统计时间T内的用户正常业务需求量是B,?t为增加的时延,则流量抑制损失量可以用公式(3)表示:
ΔLoss=?t×() (3)
公式(3)可以近似且定量地反应流量抑制现象和时间因素的关系,页面显示时长增加时用户流量需求会被抑制,小区所有用户流量损失之和为小区流量损失量,因此可用页面显示时长这项感知指标来表征流量抑制现象。endprint
2.3 模型构建及特征变量选择
页面显示时长过大引起的流量抑制受多重因素影响,包括网络覆盖、无线干扰、规划容量、信令流程、网络结构、编码方式等。从通信全流程来看(端到端分析),流量抑制既有SP运营商的内容、服务器路由等因素,也有网络质量、用户终端行为等因素,如图3所示:
在移动通信网络中,无线网质量更易受外界因素的影响,性能波动性较大,是影响流量抑制的关键,其他则视为固定因素,暂时不在本文研究范围内。流量抑制的无线侧流量模型如图4所示。
特征变量是多维度描述一个模型的量化指标,各变量之间相互影响,会由于相关性、冗余性等问题导致模型出现偏差。各特征间最好能保持独立,有时需要剔除一些不相关或冗余特征,从而减少特征个数提高模型精确度。
特征提取是数据预处理过程,可以选取与目标变量关联性强的一些特征。但是如果对数据了解程度不够的话,还可以采用相关性分析对数据进行处理。最终选取的特征应是所有特征的一个子集。流量抑制模型部分特征变量的说明如表1所示,页面显示时长作为目标变量。
3 相关性及回归模型分析
首先用相关性分析对已知特征变量做预处理,了解各变量对目标变量的相关程度以及各特征变量之间的独立性,再结合回归模型系数权重,了解特征变量对目标变量的重要程度。
3.1 特征变量的相关性分析
相关性分析是指对两个或多个具备相关性的变量进行分析,从而衡量两个变量因素的密切程度。当两个变量带有测量误差时,它们之间的相关性会削弱。常用相关性计算方法是Pearson相关系数[4-5],计算公式如下:
其中n是样本个数,Xi是特征变量,Yi是目标变量,X_和Y分别是其对应变量的均值。相关系数r的范围在-1和1之间,|r|值越大,表示连个变量之间影响越显著。
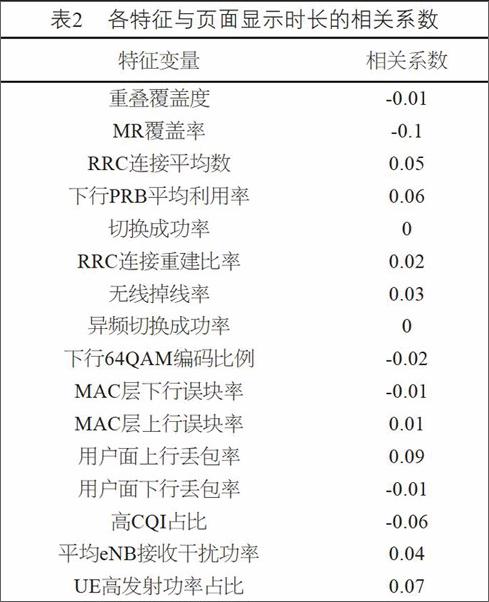
选取某地区LTE忙时(中午11点)数据作为分析样本,剔除异常样本后,各特征向量与目标变量之间的相关系数如表2所示,其中重叠覆盖度、切换成功率等特征变量与页面显示时长的相关系数极低,为精简模型可以考虑将这些特征变量从模型中剔除。
另外为检验各特征变量之间的独立性,建立特征变量之间的相关系数矩阵,因矩阵较大这里仅列出矩阵中相关系数较高的几个特征变量:RRC连接平均数与PRB利用率的相关系数是0.74;高CQI占比与下行64QAM编码比例之间的相关系数是0.7。为保证特征指标的独立性及模型精度,删除相关系数为零的切换指标、冗余指标PRB利用率(保留RRC连接平均数是因为其更直观且PRB利用率容易受限)以及下行64QAM编码比例。
3.2 多元线性回归方程
多元线性回归是一种应用较为广泛的预测模型,可通过多个特征值来解释目标值[7]。其数学模型如下:
其中Y是目标变量,本文指页面响应时长;θ是线性回归系数;X是特征变量矩阵;b为偏置常数。
多元线性回归模型的计算目的是得到回归系数θ值和偏置常数b,常用计算方法包括最小二乘法的矩阵解法[8]、梯度下降法[9]等。Matlab软件作为一种常用数据处理工具,简单易用,编程效率高,可以比较方便地得到线性回归方程并对其做显著性检验[10]。
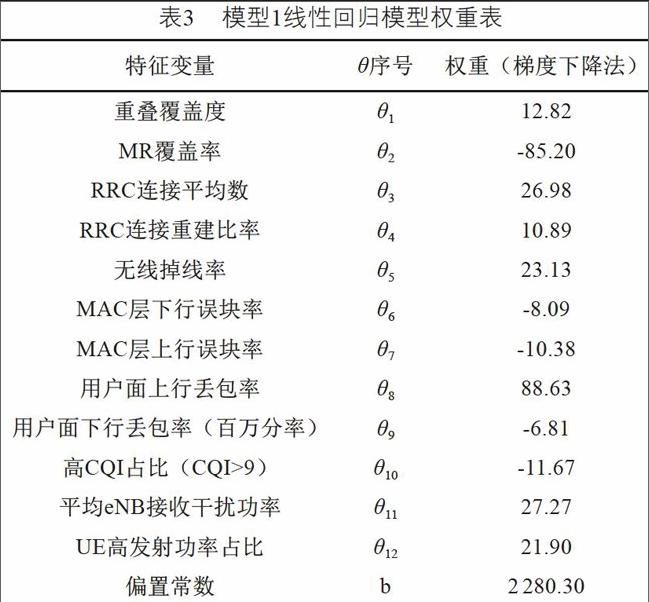
根据相关性选取的12个特征变量构建模型1,用Matlab做标准化处理,然后采用梯度下降算法得到多元线性回归模型系数和偏置常数,该结果如表3所示:
回归模型的权值大小反应特征变量对目标变量的影响程度,结合相关性分析,MR覆盖率、上行丢包率、eNB接收干扰、UE高发射功率占比、RRC连接平均数等5项对目标变量有显著影响,如图5所示:
选取图5中有显著影响的5项特征建立模型2,应用多元线性回归得到权重系数如表4所示:
对于权重系数的理解有助于了解其对应特征对页面显示时长的影响程度,比如MR覆盖率与页面显示时长负相关,覆盖率下降则页面显示时长增加。
3.3 回归方程显著性检验及偏差分析
所建立模型的多元线性回归方程对目标变量的解释是否准确,需要对回归方程进行统计意义上的显著性检验[11]。检验方法包括:判定系数检验(R2检验)、回归方程显著性检验(F检验)等。若回归方程-显著性检验未通过,可能是选择特征变量时漏掉了重要影响因素,或是特征变量与目标变量间的关系非线性。
模型1是建立的基本模型,设定显著性水平α=0.05,对其检验结果如表5所示:
整体相关系数R=0.226,判定系数R2=0.051较小,说明预测结果与目标变量之间关联性较低,预测准确性有待提升。F检验值为109.343,在置信度α=0.05时,查F检验的临界值表得到临界值F0.05(12, >1000)≈1.76,且P值也小于α=0.05,可拒绝回归方程非显著性的假设,由此认为多元性回归方程显著。均方差比较大是由于离散性比较大,模型的拟合较困难。
实际工程中为了检验模型预测效果,一般会采用比较直观的偏差分析法。偏差分析的计算方法设定如下:
偏差=abs(实际值-预测值)
准确度=1-偏差/实际值
正确率=准确度大于等于0.8的小区数量/小區总数 (6)
模型1和模型2的特征变量选取数目不同,得到的回归方程也有差别。它们的预测结果差别如何就可以通过偏差分析,了解特征变量对目标变量的解释是否满足要求以及模型的预测精度。模型1和模型2的偏差及准确度情况如表6所示:
从表6可以看出,两个模型的预测偏差差别不大,说明模型2的5项特征也可以较好地反应页面显示时长变化,在优化工作中可以重点关注。比如覆盖率不足将直接影响小区性能与用户感知,页面显示时长增加,进而抑制用户的流量需求。
决定系数以及预测偏差显示得到的多元线性回归方程精度还存在不足,原因可能是特征变量的选取有偏差,也可能模型中某些变量与页面显示时长非线性关系。特征变量的选取可在工作中继续完善,至于特征变量和页面显示时长是否非线性,比较简单的方法是用单变量的多项式拟合来检验。以RRC连接数和覆盖率两个变量与页面显示时长的关系为例,多项式拟合的结果显示具有非线性特征,所以采用线性回归分析时对目标变量的解释偏差会大些,如图6和图7所示:endprint
一般來说,当页面显示时长超过均值时就可以认为存在流量抑制现象(大约3 000 ms,如图6的A点),实际工作中可选择平均页面显示时长显著增加区域为流量抑制重点关注区,如图6的B点和图7的C点,大约4 200 ms。
4 结论
流量抑制模型的建立便于网络运营和优化人员了解LTE数据业务流失的基本原因,在工作中采取针对措施提升网络质量。由特征变量选取及建立不同的线性回归方程可了解到,页面显示时长与MR覆盖率负相关,而与用户数、上行干扰、终端发射功率等正相关,模型可用于流量抑制的预测与分析,这对网络优化工作具有实际指导意义,比如关注页面显示时长大于4.2 s的小区在某些特征上是否存在异常,或预测特定网络条件下流量抑制是否严重。模型中部分变量与页面显示时长实际是非线性关系,对模型预测精度有影响;特征变量选取也会影响模型精度,另外本文的研究还忽略了核心网的影响,这都需要在实际工作中不断改进和完善。
参考文献:
[1] 搜狐网. 中国移动尚冰:无线数据业务已成公司第一大收入来源[EB/OL]. (2016-12-20)[2017-08-28]. http://www.sohu.com/a/122104339_114877.
[2] 谢卫浩. FDD LTE业务模型和商用网统计实例[EB/OL]. (2013-10-29)[2017-08-28]. http://www.zte.com.cn/cndata/magazine/zte_technologies/2013/10_2013/magazine/201310/t20131029_411037.html.
[3] 江敏. RRC并发用户数对LTE网络影响分析[J]. 2016(1): 263-264.
[4] 周京胜. 基于用户感知的TD-LTE网络场景化扩容[J]. 电信快报, 2015(12): 28-31.
[5] 谢娟英,高红超. 基于统计相关性与K-means的区分基因子集选择算法[J]. 软件学报, 2014(9): 2050-2075.
[6] 郭红霞. 相关系数及其应用[J]. 武警工程学院学报, 2010(2): 3-5.
[7] KP Murphy. Machine Learning: A Probabilistic Perspectiv[M]. Cambridge: MIT Press Massachusetts, 2012.
[8] 易芳. 采用MATLAB的线性回归分析[J]. 兵工自动化, 2004,23(1): 68-69.
[9] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
[10] 刘勇,白林. 基于MATLAB的回归分析模型在经济预测分析中的应用[J]. 中国管理信息化, 2008,11(5): 69-71.
[11] 贾俊平,何晓群,金勇进. 统计学[M]. 北京: 中国人民出版社, 2015.endprint
