海量数据干扰下冗余数据高性能消除方法*

茹 蓓， 李 虹(. 新乡学院 计算机与信息工程学院， 河南 新乡 453003； . 吉林省质监检测基地 吉林省纤维检验处， 长春 3003)

控制工程

海量数据干扰下冗余数据高性能消除方法*

茹 蓓1， 李 虹2
(1. 新乡学院 计算机与信息工程学院， 河南 新乡 453003； 2. 吉林省质监检测基地 吉林省纤维检验处， 长春 130103)

针对海量数据处理过程中大量相似特征会给数据分类造成冗余干扰，在分类中心确定时出现多次校验、重复等弊端，提出一种海量数据干扰下冗余数据高性能消除方法.采用主动采样方法提取海量数据干扰下冗余数据特征，并对其进行分类.引入均值漂移传递函数对冗余数据进行分类处理，获取冗余数据活跃程度，实现冗余数据的高性能消除.结果表明，相比传统的消除方法，高效消除方法性能良好，所需时间短，具有一定的优越性.

海量数据； 干扰； 冗余数据； 高性能； 消除方法； 改进； 均值； 传递函数

随着计算机技术与信息处理技术的快速发展，许多领域的信息被储存在计算机系统中，形成海量数据，使得其存储和管理成为相当棘手的问题[1-2].虽然如今存储设备容量越来越大，但也无法满足处理数据量的增长需要[3-4]，形成了大量的冗余数据.而对冗余数据进行高效消除、减轻数据存储负担、提高数据存储效率成为了近年来信息处理技术的研究热点，受到广大学者的广泛关注，也出现了很多有效方法[5-7].

文献[8]提出局部均值分解的消除方法，采用数值模拟把线性、多项式及指数趋势项融入至要消除的数据中进行消除，该方法可对冗余数据进行消除，但消除过程需要一定约束条件；文献[9]提出规则分段技术法，把多个冗余数据进行消除，但该方法只能应用到小聚类环境中；文献[10]提出一种基于均值分解的消除方法，在CPU里设定一个特别的任务切换专用数据链路，实现在CPU硬件资源限制状态时进行数据存储，引入Hyper-Scheduling法对冗余数据进行消除，但是该方法误差较大.

针对上述问题的产生，本文提出一种新的海量数据干扰下冗余数据高性能消除方法，采用主动采样方法提取数据特征，并引入均值漂移传递函数对冗余数据进行分类，相比传统的消除方法具有一定的优越性.

1 海量数据干扰下冗余数据分类

由于海量数据的相似特征容易造成循环分类、多次处理等问题，因此，需要专门针对相似性干扰提取冗余数据特征，并根据特征对冗余数据进行分类，加快消除速率.

1.1 冗余数据特征获取

海量数据在特征相似的环境下，会形成冗余干扰，在进行冗余数据分类之前，采用主动采样方法提取海量数据冗余数据特征.

假设最初训练数据集的全部样本数是N，大类样本数为Nmax，小类样本数为Nmin，则当大类样本数大于小类样本数据，即Nmax>Nmin，对小类中每个样本的分类密度ρl定义为

ρl=Ml/K(l=1，2，…，Nmin)

(1)

式中：K为空间中基于欧式距离的最近邻数目；Ml为K个最近邻数目中属于大类的样本数.很明显，ρl∈[0，1]，其密度分布表达式为

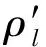
(2)

假设对p个样本的第j个输出值和目标值分别是ypj(τ)和dpj，则特征提取约束条件为

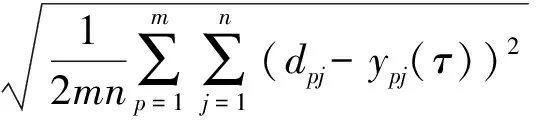
(3)

式中：τ为迭代数目；n为输出数据量；m为最后训练数据集的数量.分类迭代次数表达式为

w(τ+1)=w(τ)+ηΔw(τ)+α(w(τ)-

w(τ-1))

(4)

式中：η为迭代速率；α为动量因子.此时提取过程收缩量为

(5)

式中：φpj(τ)为输入量总和；o(τ)为冗余数据输出量.在此基础上，提取海量数据干扰下冗余数据特征.

假设有一个标准的样本数据集Nh，激励函数为g(x)，采集的样本数为Ns，样本为(xq，tq)，其中xq=[xq1，xq2，…，xqn]T∈Rn且tq=[tq1，tq2，…，tqm]T∈Rm，则建立的冗余数据提取模型为

(6)

式中，bq为冗余数据偏置.

1.2 冗余数据特征分类

在获取冗余数据特征的基础上，采用线性频谱分析法，对海量数据干扰下的冗余数据特征进行分类，为改进冗余数据消除方法提供基础依据.

在海量数据干扰下，冗余数据特征通常在时间及空间上的标点为离散状态，所以冗余数据分类过程及有关理论也应建立在离散状态下.当在采集面z=z0处时，其分类分量表示为

S+(zm)=W+(zm，z0)S+(z0)

(7)

式中：W+(zm，z0)为从z0到zm的分类算子；S+(z0)为分类集合.在进行冗余数据分类时，往往只需要去除M阶多次分类，故提取的前M项分类结果表示为

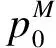
p(z0)S+(z0)

(8)

式中：p(z0)为记录的原始数据；t(z0)为数据特征.

假设初始样本冗余数据采样频率为f0，计算确定冗余数据提取结果为

(9)

采用线性频谱分析法得到冗余数据的适应值函数，对海量数据干扰下的冗余数据进行分类，则其冗余数据的分类约束函数为

F=XmaxA+(1-Xmax)B

(10)

式中：A为分类准确率；B为消减百分比.对异常数据的类内离散度集合进行加权处理，得到分类结果为

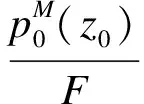
COVmin)]

(11)

式中，COVmax、COVmin分别为样本的最大协方差和最小协方差.

2 海量数据干扰下冗余数据消除

在对冗余数据进行分类的基础上，假设LU为U时刻采集分类后的冗余数据，LV为V时刻采集分类后的冗余数据，则其冗余数据采集速度可表示为

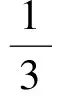
Smin(LU，LV))

(12)

式中，Smax，Savg，Smin分别为最大速度、平均速度、最小速度差异程度的绝对值.此时LU与LV间的位置距离获取表达式为

D=V(LU，LV)dist(LU，LV)

(13)

式中，dist()为冗余数据间的欧氏距离.

为了进一步对冗余过程进行改进，引入相似度概念，根据冗余数据的突出特征获取整体相似度.对于任意第i个冗余数据，其整体相似度可表示为

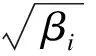
(14)

式中：Ci为相关度系数；βi为冗余数据的突出特征.

对于单个冗余数据来说，它包括γi个冗余数据特征.冗余数据整体相似度可表示成突出特征βi的结构相似度.对整体相似度进行加权处理，则其加权平均数表达式为

(15)

式中：si为i个冗余数据的加权平均数；I为冗余数据集上的特征数量.显然整体速度大，冗余数据特征越明显，进行消除越彻底；反之，冗余数据特征越不显著，消除效果越差.为了能在冗余数据特征不显著的情况下，也能对冗余数据进行消除，引入了均值漂移传递函数对冗余数据进行处理，提高了方法的消除性能.

假设数据集O中存在Hi个冗余数据，则均值漂移传递函数可表示为

(16)

(17)

式中：tmin为冗余数据最短活跃时间；tmax为冗余数据最长活跃时间；t为总活跃时间.由此可知，Y越大，说明冗余数据越活跃，消除效果越好；反之，Y越小，说明冗余数据不活跃，消除效果越差.

3 实验结果分析

为了验证本文所设计的冗余数据消除方法的性能，进行了实验对比分析.实验电脑的硬件设置为：16 Gbit内存，Xeon E5606处理器，主频2.13 GHz、14 Tbit RAID6磁盘阵列(16个1 Tbit磁盘，其中2个是校验盘)以及120 Gbit的闪存(SVP200S37A120G)，配置的操作系统为Ubuntn12.04，测试数据集为GCC、SciLab、Linux，数据集的数据特征设置如表1所示.

测试数据集合将3种数据集结合在一起，由于3种数据集合中存在大量的相似数据，这种数据的相似性会形成实验环境中的冗余干扰，符合干扰环境条件.

3.1 准确率实验分析

为了验证本文方法的有效性，在数据量一定的情况下，采用文献[8]局部均值分解的消除方法、文献[9]规则分段技术法与改进方法进行消除准确率方面的对比.在固定数据量情况下，采用不同方法进行冗余数据消除试验，实验准确率用消除数据量与原始数据量的比值表示，取10次结果平均值进行统计.实验在GCC数据集中进行，其三维数据冗余环境模拟如图1所示(x、y、z轴表示数据空间的存储位置).

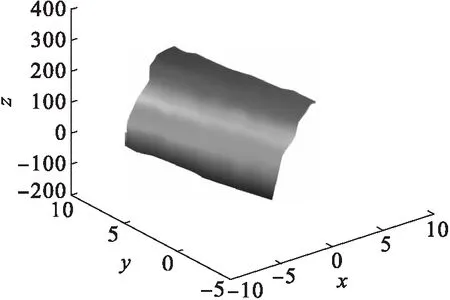
图1 GCC冗余环境模拟Fig.1 GCC redundant environment simulation

在图1冗余环境中进行不同方法的准确率对比研究，统计结果如图2所示.

由图2可知，在GCC数据集中，采用局部均值分解法其准确率可达到49.3%；采用规则分段技术法时，其消除准确率约为68.1%，两种算法随着数据量的增加，均出现准确率下降的趋势，不适合大量数据应用；采用改进方法时，其消除准确率约为79.7%，其整体要比局部均值分解法、规则分段技术法的准确率提高了约30.4%、11.6%，具有一定的优越性.在冗余干扰的环境下，本文方法可以运用有限次数的分类使得冗余数据被迅速排除在聚类中心之外；而其他方法都需要进行多次的对比和聚类中心校验操作，大幅度降低了聚类的效率，使得干扰数据无法被有效排除.

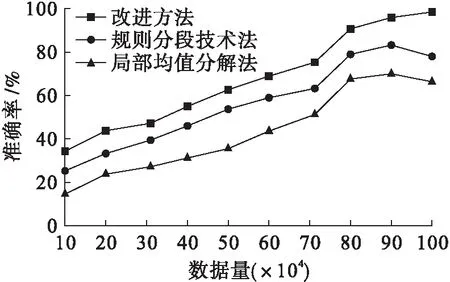
图2 GCC数据集冗余数据消除准确率对比Fig.2 Comparison in elimination accuracyof redundant data in GCC dataset

3.2 效率对比分析

采用文献[8]局部均值分解的消除方法、文献[9]规则分段技术法与改进方法进行消除效率方面的对比，实验在SciLab和Linux数据集中进行，其三维数据冗余环境模拟如图3所示.

图3 SciLab和Linux冗余环境模拟Fig.3 SciLab and Linux redundantenvironment simulation

在图3冗余环境中进行不同方法效率方面的对比研究，统计结果如图4所示.

由图4可以看出，在数据量一定的情况下，采用局部均值分解法时，其消除平均时间约为7.23 s；采用规则分段技术法时，其消除所需时间约为5.53 s，且随着数据量的增加，消除时间存在多处波动，稳定性较差；采用改进消除方法时，其消除所需时间约为3.42 s，相比传统的方法，本文方法耗时降低明显，具有一定的优势.耗时是最能反映算法优劣性的参考数据，在数据流增加的环境下，冗余干扰强度势必成倍增加，本算法虽然在后期冗余去除过程中耗时略有增加，但是优化效果明显.

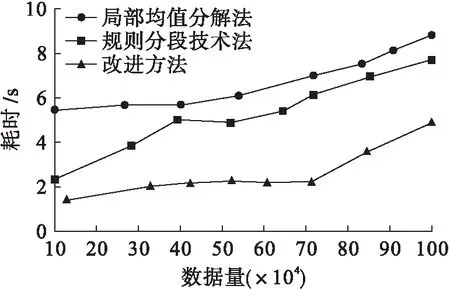
图4 不同算法下消除所需时间对比Fig.4 Comparison in elimination timewith different algorithms

4 结 论

针对传统冗余数据消除方法一直存在消除时间长、性能差的问题，本文提出一种冗余数据高性能消除方法.采用主动采样方法提取海量数据干扰下冗余数据特征，通过线性频谱分析法对海量数据干扰下的冗余数据进行分类，并以此为基础计算出冗余数据的相似度，引入均值漂移传递函数对冗余数据进行处理，获取冗余数据活跃程度，实现海量数据干扰下冗余数据的高性能消除.仿真实验结果表明，相比传统的消除方法，改进方法的准确率及效率均有所提高，具有一定的优越性.

[1] 宛婉，周国祥.Hadoop平台的海量数据并行随机抽样 [J].计算机工程与应用，2014，50(20)：115-118.

(WAN Wan，ZHOU Guo-xiang.Massive data parallel random sampling based on Hadoop [J].Computer Engineering and Applications，2014，50(20)：115-118.)

[2] 李志虹.基于遗传迭代优化的云计算下海量数据分类查询 [J].科技通报，2015，31(6)：34-36.

(LI Zhi-hong.Classification query of huge amounts of data in cloud computing environment based on genetic optimization [J].Bulletin of Science and Technology，2015，31(6)：34-36.)

[3] 钱勤，张瑊，张坤，等.用于入侵检测及取证的冗余数据删减技术研究 [J].计算机科学，2014，41(增刊2)：252-258.

(QIAN Qin，ZHANG Jian，ZHANG Kun，et al.Technical study of reducing redundant data for intrusion detection and intrusion forensics [J].Computer Science，2014，41(Sup2)：252-258.)

[4] 王永利，王川，蒋效会，等.基于时空布隆过滤器的RFID冗余数据清洗算法 [J].南京理工大学学报，2015，39(3)：253-259.

(WANG Yong-li，WANG Chuan，JIANG Xiao-hui，et al.RFID duplicate removing algorithm based on temporal-spatial Bloom filter [J].Journal of Nanjing University of Science and Technology，2015，39(3)：253-259.)

[5] 孟庆娟，曹青媚，马占飞.海量冗余数据干扰下的网络数据捕获和分析系统研究 [J].现代电子技术，2016，39(16)：27-30.

(MENG Qing-juan，CAO Qing-mei，MA Zhan-fei.Research on network data capture system and analysis system under interference of massive redundant data [J].Modern Electronics Technique，2016，39(16)：27-30.)

[6] 王乐，王芳.网络数据库中冗余环境下的高效数据定位仿真 [J].计算机仿真，2016，33(4)：364-367.

(WANG Le，WANG Fang.Simulation of efficient data localization in network database under redundant environment [J].Computer Simulation，2016，33(4)：364-367.)

[7] 聂军.基于 K-L 特征压缩的云计算冗余数据降维算法 [J].微电子学与计算机，2016(2)：125-129.

(NIE Jun.A data reduction algorithm based on K-L feature compression for cloud computing [J].Microelectronics & Computer，2016(2)：125-129.)

[8] 韩晓慧，杜松怀，苏娟，等.基于局部均值分解的触电故障信号瞬时参数提取 [J].农业工程学报，2015，31(17)：221-227.

(HAN Xiao-hui，DU Song-huai，SU Juan.Extraction of biological electric shock signal instantaneous amplitude and frequency based on local mean decomposition [J].Transactions of the Chinese Society of Agricultural Engineering，2015，31(17)：221-227.)

[9] 刁爱军.基于压缩特征编码的混合云冗余数据删除算法 [J].科技通报，2015，31(8)：42-44.

(DIAO Ai-jun.Hybrid cloud redundant data delete algorithm based on feature code compression [J].Bulletin of Science and Technology，2015，31(8)：42-44.)

[10]赵志科，张晓光，王新.基于局部均值分解的机械振动信号趋势项消除方法 [J].郑州大学学报(工学版)，2014，35(5)：100-104.

(ZHAO Zhi-ke，ZHANG Xiao-guang，WANG Xin.Trend elimination method of mechanical vibration signal based on local mean decomposition [J].Journal of Zhengzhou University(Engineering Science)，2014，35(5)：100-104.)

Highperformanceeliminationmethodforredundantdataundermassivedatainterference

RU Bei1, LI Hong2

(1. School of Computer and Information Engineering, Xinxiang University, Xinxiang 453003, China; 2. Office of Fiber Inspection of Jilin Province, Quality Supervision and Inspection Base of Jilin Province, Changchun 130103, China)

Aiming at the problem that in the data treatment process of massive data, a lot of similar characteristics can bring the redundant interference to the data classification, and cause such drawbacks as multiple check and repetition during the determination with the classification center, a high performance elimination method for redundant data under the massive data interference was proposed. With the active sampling method, the redundancy data feature under the massive data interference was extracted and classified. In addition, the mean shift transfer function was introduced to perform the classification of redundant data, obtain the redundant data activity and realize the high performance elimination of redundancy data. The results show that compared with the traditional method, the high performance elimination method has good properties, short processed time and certain superiority.

massive data; interference; redundant data; high performance; elimination method; improvement; mean value; transfer function

2016-11-21.

河南省科技厅科技攻关资助项目(172102210445)； 河南省科技厅软科学研究资助项目(152400410345)； 河南省教育厅资助项目(15A520093).

茹 蓓(1977-)，女，河南新乡人，副教授，硕士，主要从事软件开发、信息安全等方面的研究.

* 本文已于2017-10-25 21∶13在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20171025.2113.068.html

10.7688/j.issn.1000-1646.2017.06.16

TP 311

A

1000-1646(2017)06-0686-05

(责任编辑：景 勇 英文审校：尹淑英)