基于分数阶自抗扰技术的核电站稳压器压力控制*
2017-11-14何柏青南昌理工学院电子学院南昌330000
梁 华, 何柏青(南昌理工学院 电子学院, 南昌 330000)
基于分数阶自抗扰技术的核电站稳压器压力控制*
梁 华, 何柏青
(南昌理工学院 电子学院, 南昌 330000)
针对传统PID在复杂的核电站稳压器控制系统中无法获得良好的控制效果的问题,提出了分数阶自抗扰控制器(FOADRC).该控制器将分数阶控制器与自抗扰控制器相结合,不仅具备分数阶控制器的快速与高精度特点,还具备自抗扰控制器的强鲁棒性和抗扰动性能,解决了ADRC技术中非线性状态误差反馈控制律调参较困难的问题.建立的稳压器压力控制的Simulink仿真模型表明,分数阶自抗扰控制器与传统PID控制和ADRC控制相比具有更加优良的性能指标.
核电站; 稳压器; 压力控制; 分数阶PIλDμ控制器; ADRC控制; PID控制; FOADRC控制; Simulink仿真
稳压器是核电站一回路中的重要设备之一,其作用是调节和维护一回路冷却剂的压力,从而保证稳压器的压力和水位维持在设定值上.但是稳压器是一个非常复杂的系统(惯性大,干扰多等),在实际中很难获得稳压器的精确模型.因此,利用传统的控制算法就很难获得令人满意的控制效果[1].针对稳压器的控制,多采用传统的PID控制,由于其自身局限性,控制效果不是很理想,抗干扰能力也较差.为此,研究人员在分数阶理论研究的基础上,又提出了分数阶PIλDμ控制器,其比传统PID控制器多了积分阶次λ和微分阶次μ,增加了控制器的灵活度,实现PID由点到面的控制,相比于传统PID控制,它继承了传统PID控制的优点并具有更灵活的结构和更强的鲁棒性,其控制律的变化也更加精确,因此,可获得更优的动态性能和鲁棒性能[2].针对PID控制的自身局限性(快速性与超调量的直接矛盾,抗干扰能力差等),研究员韩京清教授提出了自抗扰控制技术,主要由安排过渡过程(TD)、扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)等部分组成,其不依赖被控对象的精确数学模型,能够将系统的未建模动态和未知外界扰动都归结为对系统的总和扰动而进行估计和补偿,可以很好地改善传统PID控制的不足[3].
本文考虑到分数阶PIλDμ控制器和自抗扰控制技术各自的优点,提出了分数阶自抗扰控制器(FOADRC),该控制器在分数阶PIλDμ控制器的基础上引入了自抗扰的安排过渡过程和扩张观测器,使其既具有分数阶控制器的快速性和高精度的性能,又具有自抗扰控制器的强鲁棒性等.通过理论分析和仿真结果表明,分数阶自抗扰控制器(FOADRC)比传统PID控制和自抗扰控制都具有更加优良的动、静态性能指标.
1 分数阶控制器
1.1 分数阶微积分理论
分数阶微积分是指微积分的阶次不再是整数,可以是分数甚至复数,它可以看作是传统PID控制的推广.常用的分数阶微积分的定义有三种,分别为Grunwal-Letnikov定义、Riemann-Liouville定义和Caputo定义[4],其中,连续的分数阶微积分算子的表达式为
(1)
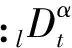
1.2 分数阶PIλDμ控制器
分数阶PIλDμ控制器是整数阶PID控制器的广义表达式,是将整数阶的积分项λ和微分项μ的阶次扩展到分数领域,其控制器的输出可以表示为
u(t)=Kpe(t)+KiDλe(t)+KdDμe(t)
(2)
式中:D为分数阶微积分基本操作算子的简化符号;e(t)为系统误差;λ为积分阶次,λ>0;μ为微分阶次,μ>0;Kp、Ki、Kd均为控制器的控制参数,并与整数阶PID意义一样,分别为比例系数、积分系数和微分系数.
经拉普拉斯变换可以得到分数阶PIλDμ控制器的传递函数,即
G(s)=Kp+Kis-λ+Kdsμ
(3)
式中,s为拉普拉斯算子.
由式(3)可以看出,整数阶PID控制器是分数阶PIλDμ控制器的积分项λ和微分项μ取特殊值的情况.因此,分数阶PIλDμ控制器可以实现PID由点到面的控制,通过合理的参数整定,分数阶PIλDμ控制器能更好地、更精确地提高系统控制效果.
1.3 分数阶微积分算子的近似与改进
实际上,在分数阶微积分的定义下,分数阶PIλDμ控制器是一个无限维数的滤波器.为了实现分数阶控制,本文采用Oustaloup近似算法以及改进算法,其中,Oustaloup滤波器在一个有限的频率段(wb,wh)内对微积分算子的近似可表示为
(4)
(5)
(6)
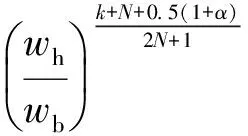
(7)
式中:wh、wb分别为Oustaloup滤波器近似频率范围的上下限;N为滤波器的阶次.
由于该算法在近似频率两端的近似效果不是很理想,因此,本文参考了文献[5]提出的改进算法,该算法是将分数阶算子用分数阶传递函数近似,即
(8)
式中,m、n为常数,均大于0.在wb (9) 联合式(8)、(9)可以得到微积分的近似公式,即 (10) 式中,s为拉普拉斯算子,s=jw,j为虚数单位. 自抗扰控制器(ADRC)由非线性跟踪微分器(TD)、非线性扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)三部分组成.该控制策略对经典PID控制做了四个方面的改进:1)安排了过渡过程;2)采用跟踪微分器对被控对象提取微分信号;3)由非线性扩张观测器实现扰动的估计和补偿;4)由误差的P、I、D的非线性组合构成非线性PID控制器[6].假设被控对象为 (11) 式中:f(x1,x2)为未知量;b、u为已知量. 以二阶ADRC为例介绍其各部分的算法[7],典型二阶自抗扰控制器的结构如图1所示. 图1 自抗扰控制器的基本结构Fig.1 Basic structure of ADRC 2.1 非线性跟踪微分器 跟踪微分器TD为参数输入安排过渡过程,得到光滑的输入信号,并提取其微分信号,即向TD输入信号v(t),可以得到跟踪信号v1(t)和微分信号v2(t).二阶离散形式的非线性微分跟踪器可描述为 (12) 式中:e为系统误差;v1为跟踪信号;v2为微分信号;r为速度因子;h0为滤波因子;fhan()为最优综合控制函数,其表达式为 (13) (14) 2.2 扩张状态观测器 扩张观测器(ESO)是自抗扰控制器的精髓,扩张观测器能够将系统内部和外部扰动均作为系统的扩张状态变量进行动态观测和补偿,使控制器具有很强的鲁棒性.扩张观测器状态描述表达式为 (15) 式中:β1、β2、β3为系统参数,均大于零;z1为输出y的跟踪信号;z2为输出的微分信号;z3为对扰动和不确定性的估计量;u为被控对象输入信号;b为常数;fal()为饱和函数,其作用为抑制信号抖振,其表达式为 (16) 式中,δ通常取值为采样步长h. 2.3 非线性误差反馈控制律 针对传统PID控制形式为P、I、D的线性组合,该方式显然不是最佳组合形式,可以在非线性范围内寻找一种更好的组合方式.其中,一种PD形式的非线性组合可描述为 (17) 式中,β11、β12为增益系数,类似于PD控制器的比例系数和微分系数.其中,扰动补偿过程为 u=u0-z3/b0 (18) 式中,b0为补偿因子.ADRC控制器中的参数包括r0、h0、β1、β2、β3、β11、β12、h1和b0,其中,r0、h0、β1、β2、β3和h1均与系统的采样步长有关,其关系式[8]为:r0=0.001/h2,h0=5h,β1=1/h,β2=1/(3h2),β3=1/(32h3),h1=10h.增益系数β11、β12与PID控制器中的比例微分作用相当,则有Kp=β11,Kd=β12.补偿因子b0相当于PID控制器的积分增益,则有Ki=b0.对于上述参数,本文不能把其当作精确的参数,在实际应用中,应该作为参考值,再在其附近仔细寻找合适的参数. 针对上述两种控制器的各自优缺点,本文设计了分数阶自抗扰控制器(FOADRC).一方面,该控制器利用分数阶PIλDμ控制器相角范围广、快速性好和精度高等特点来替换传统ADRC控制器中非线性误差反馈控制律,用以提高ADRC控制器的性能,同时也克服了非线性误差反馈控制律带来的高频颤振和参数调整困难等问题.由于分数阶积分环节的引入,可以改善整数积分环节导致闭环响应速度缓慢,调节时间长,容易产生振荡,积分饱和引起的控制量饱和等负面影响.另一方面,ADRC中的非线性扩张状态观测器可以实现对被控对象扰动误差的估计补偿,同时也增强了分数阶PIλDμ控制器的抗干扰能力.本文涉及的分数阶自抗扰控制器的结构如图2所示. 图2 分数阶自抗扰控制器结构Fig.2 Structure of FOADRC 稳压器压力控制的原理如图3所示.该控制系统由PID控制器、函数发生器(加热器用于升压,喷淋阀用于降压)和继电器(通断式加热器和保护阀)等构成,用于压力的控制.系统的压力传感器将不断检测压力信号,实时地跟设定值进行做差对比,并将误差信号送给常规的PID控制器,从而使相关的设备产生动作.本文将其中的PID控制用分数阶自抗扰控制来代替. 图3 压力控制系统原理图Fig.3 Principle diagram of pressure control system 根据上述原理,通过在线辨识能够得到压力控制系统的传递函数.文献[9]得出的模型为 (19) 本文针对稳压器中压力控制系统分别采用传统PID控制、ADRC控制和FOADRC控制进行对比分析.其中,PID的参数为Kp=100,Ki=0.11,Kd=500;ADRC的主要参数为r0=0.4,h0=0.05,β11=800,β12=500,β1=20,β2=133.33,β3=33,b0=1.776/3 300;FOADRC中分数阶的参数为Kp=13,Ki=90.25,Kd=800,λ=0.85,μ=0.65.通过观察稳压器压力的实际仿真结果可以明显看出,FOADRC控制与ADRC控制和常规PID控制相比,其超调量减小,而且调节时间、峰值时间和上升时间等都明显缩短,稳态误差较小,控制精度较高,具有较好的动态响应性能,能够提高稳压器压力的控制性能,仿真结果和数据如图4和表1所示. 图4 压力控制系统仿真图Fig.4 Simulation diagram for pressure control system 表1 压力的动态性能指标比较Tab.1 Comparison in dynamic performanceindexes of pressure 为了验证本文所设计控制器的鲁棒性,在仿真时间为50 s时加入幅值为0.1 MPa的阶跃干扰来模拟核电站运行过程中的不确定影响因素,仿真结果如图5所示.由图5可知,在受干扰的情况下,传统PID控制器的超调量较大,且在19.09 s内才完成调节,需调节的时间较长;ADRC控制器的超调量较小,需要2.12 s完成调节;而FOADRC控制器的超调量最小,干扰对控制器的参数影响最小,且在0.035 s内完成调节,说明能更快地回到稳态值.由此说明,FOADRC控制器受负载的影响较小,具有很好的抗干扰性和鲁棒性. 图5 加干扰下的阶跃响应Fig.5 Step response with added disturbance 针对复杂时变多干扰的核电站稳压器,本文将自抗扰控制器(ADRC)与分数阶PIλDμ控制器相结合,设计了分数阶自抗扰控制器(FOADRC),并首次用于核电站稳压器压力的控制系统中.通过实际仿真实现了压水堆核电站稳压器压力的有效控制.通过与传统PID控制和ADRC控制相对比,无论在跟踪性还是抗干扰能力方面都大大增强,既具有分数阶PIλDμ控制器的快速和高精度的性能,又拥有自抗扰控制器的强鲁棒性和抗干扰能力.本文为分数阶自抗扰控制器在核电站稳压器上的应用提供了参考. [1] 张国铎,杨旭红,卢栋青,等.核反应堆稳压器水位和压力控制系统研究 [J].化工自动化及仪表,2013,40(1):35-38. (ZHANG Guo-duo,YANG Xu-hong,LU Dong-qing,et al.Research on water level and pressure control system of nuclear reactor regulator [J].Control and Instruments in Chemical Industry,2013,40(1):35-38.) [2] 鲍雪,王大志,杨永生.基于CAPSO算法的修正炮弹分数阶控制器设计 [J].仪器仪表学报,2015,36 (11):2556-2561. (BAO Xue,WANG Da-zhi,YANG Yong-sheng.Design of the fractional order controller for correction projectiles basedon the improved particle swarm optimization algorithm [J].Chinese Journal of Scientific Instrument,2015,36(11):2556-2561.) [3] 韩京清.自抗扰控制技术:估计补偿不确定因素的控制技术 [M].北京:国防工业出版社,2016. (HAN Jing-qing.Active disturbance rejection control technique:the technique for estimating and compensating the uncertainties [M].Beijing:National Defense Industry Press,2016.) [4] 车树涛.分数阶PIλDμ蒸汽压力控制系统算法研究 [D].哈尔滨:哈尔滨理工大学,2012. (CHE Shu-tao.Research on algorithm of the steam pressure system controled by fractional-order PIλDμ[D].Harbin:Harbin University of Science and Technology,2012.) [5] 吴振宇,赵亮,冯林.基于分数阶PID控制器的智能车控制 [J].控制工程,2011,18(3):401-404. (WU Zhen-yu,ZHAO Liang,FENG Lin.Control of intelligent vehicle based on fractional order PID [J].Control Engineering of China,2011,18(3):401-404.) [6] 刘金琨.先进PID控制MATLAB仿真 [M].北京:电子工业出版社,2011. (LIU Jin-kun.Advanced PID control about MATLAB simulation [M].Beijing:Publishing House of Electronics Industry,2011.) [7] 苏思贤.自抗扰控制器及其应用研究 [D].无锡:江南大学,2011. (SU Si-xian.Active disturbance rejection controller and its application research [D].Wuxi:Jiangnan University,2011.) [8] 陈红,曾建,王广军.蒸汽发生器水位的自抗扰控制 [J].中国电机工程学报,2010,30(32):103-106. (CHEN Hong,ZENG Jian,WANG Guang-jun.Stam generator water level control based on active distur-bance rejection control [J].Proceedings of the CSEE,2010,30(32):103-106.) [9] 林静.基于自抗扰的核电站稳压器控制系统研究 [D].上海:上海电力学院,2014. (LIN Jing.Research on control system of pressurizer in nuclear reactor based on active disturbances rejection controller [D].Shanghai:Shanghai University of Electric Power,2014.) Pressurecontrolofpressurizerinnuclearpowerstationbasedonfractionalorderautodisturbancerejectiontechnique LIANG Hua, HE Bo-qing Aiming at the problem that the traditional PID can not obtain good control effect in the complex pressurizer control system of nuclear power station, a fractional order auto disturbance rejection controller (FOADRC) was proposed. Both fractional order controller and auto disturbance rejection controller (ADRC) were combined in the present controller, so that the controller could not only have the rapidity and high precision features of fractional order controller, but also have the strong robustness and disturbance rejection performance of ADRC. Therefore, the problem of difficult parameter adjustment in the nonlinear state error feedback control law in ADRC technology gets solved. The established Simulink simulation model for the pressure control of pressurizer reveals that compared with the traditional PID control and ADRC control, the FOADRC has better performance indexes. nuclear power station; pressurizer; pressure control; fractional order PIλDμcontroller; ADRC control; PID control; FOADRC control; Simulink simulation 2017-03-28. 江西省教育厅教改课题基金资助项目(JXJG-16-25-8). 梁 华(1984-),女,江西南昌人,讲师,硕士,主要从事自动化控制和信息处理等方面的研究. * 本文已于2017-10-25 21∶13在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20171025.2113.046.html 10.7688/j.issn.1000-1646.2017.06.18 TL 361 A 1000-1646(2017)06-0697-05 (责任编辑:钟 媛 英文审校:尹淑英)2 自抗扰控制技术

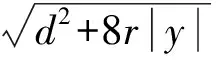
3 分数阶自抗扰控制器的设计

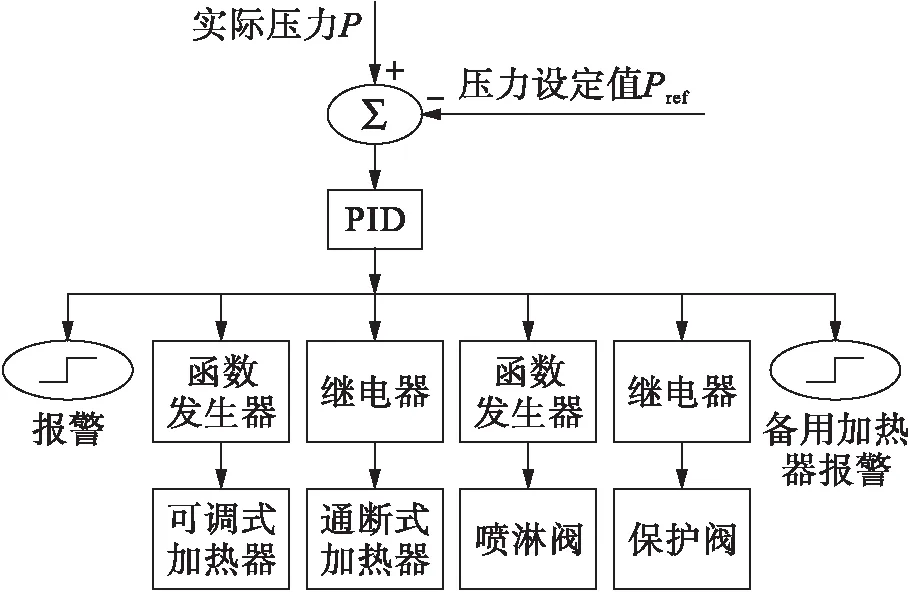
4 系统仿真
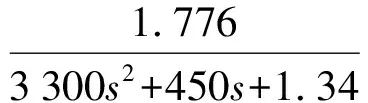



5 结 论
(School of Electronics, Nanchang Institute of Technology, Nanchang 330000, China)
