让创新意识在自由探索中生根发芽
2017-11-13陈选峰
【摘 要】培养学生的创新意识是教育教学的重要目标,因此,教师可以通过自由探索氛围的营造,使学生想探索,培育创新意愿;保证充分自由探索的时间,静待创新之花的盛开;提供指向本源的可选择的自由探索材料,结出创新之果;形成氛围、时间、空间的“创新场”,让学生的创新意识生根发芽。
【关键词】创新意识 自由探索 氛围 时间 空间
数学学习中,“唤起学生的创新欲望,激发学生的创新思维,经历创新性学习的过程”已成为当下数学教师的普遍共识。“营造独立思考、自由探索的良好环境” 能有效培养学生的创新意识,这俨然成为一线教师的普遍教学意识。怎样从操作层面使学生在课堂上自由探索,让创新意识在学习中生根发芽,进而开花结果?笔者结合自己的教学实践谈些具体做法。
一、营“自由探索”氛围,育创新之意
教师在数学教学时应创设一种能让学生自由探索的教学氛围,并适当鼓励以激发学生创新的欲望与兴趣。
首先,创设不唯师、不唯书的氛围。创新的核心要素是质疑的品质与意识。在课堂学习过程中,当学生的认识与教师、教材答案产生冲突时,是全盘接受还是在挑战权威中学习,这既关系到学生对知识的真理解,更关系到学生质疑品质的培养。
其次,鼓励争论自由。表现在数学课堂上的自由争论,既可以和教师争论,也可以和同伴争论。通过争论,形成共鸣,或相同,或相异,都已不是主要目的,争论过程中学生养成自由探索意识,提升自由思维品质尤显重要。
例如,五年级下册的单式折线统计图,我们改编材料(如图1)。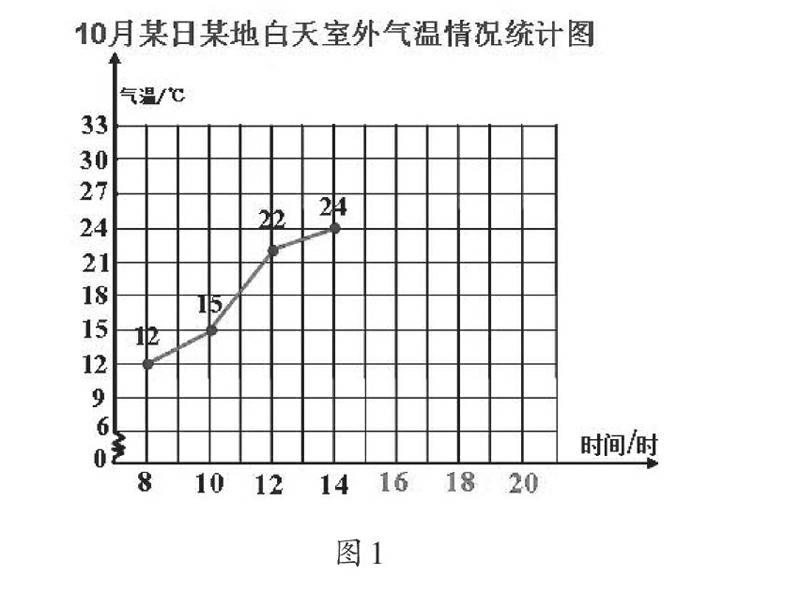
(1)引导学生观察例题中的折线统计图。
(2)根据观察到的结果,估计16时、18时、20时的气温,并将统计图补充完整。
(3)展示学生画法,并开展自由争论。
学生展示作品中的折线有继续升高的变化情况,也有折线向下气温向下变化的。接着教师鼓励学生自由争论,通过争论大家认识到,从发展趋势上看气温不断升高,但可能会受太阳光照等影响,气温在下午2时可能最高,其折线统计图变化趋势一般会逐渐下降;如果碰到极端天气则可能在某一时间快速下降或上升。
最后,鼓励自由质疑。小学生尤其是低年级的学生是很喜欢问为什么的,但在课堂上却往往是有质疑问难时间,无质疑问难之人。学生不敢问、不想问、不会问的现象较为普遍。究其原因,与其有无自由质疑的机会与氛围相关。
为培养学生自由质疑的习惯,教师一般从接手一个班级开始的第一个学期起专门在课堂上留下至少5分钟时间进行质疑问难,告诉学生:现在是质疑时间,请大家对刚才老师或同学的观点及学到的知识进行自由质疑。开始实施时一般提供方法供学生参考,如怎么提“为什么”。教师提出:你有提为什么的自由,你既可以针对自己不懂的内容,也可以针对其他同学可能会不懂的内容。接下来,我和学生共同商议,任何学生可以在任何时候、针对任何内容提出质疑。
这样,学生知道质疑既是自己的一种权利,也是一种自由。而为质疑做准备,既需认真倾听他人观点,还需主动思维,寻求自己个性化的方法,从而达到逐步培养学生创新意识的目的。
二、留“自由探索”时间,开创新之花
一个人的创新能力并不是一朝一夕所能形成的,也不是某一节课所能培养的,这是一个长期的过程。但并不是说在课堂学习中对于创新能力的培养无所作为,我们要做的是在学生自由探索时留足时间,保护学生的求异思维,激发学生的创新欲望。这如同埋下创新的种子,让它在合适的时间、合适的“温度”下生根发芽。
(一)留足学生自由探索的时间
教师要舍得花时间去等待学生的“慢”探索。在学生探索的过程中一般不指导、不暗示,尽量让学生自由探索。如碰到困难应由学生主动提出,教师给予鼓励与少量点拨。
如在教学人教版一年级下册第86页数学游戏时(如图2)。
课后,李同学对这道题兴趣高漲,主动请笔者再出题考考他。笔者先出一个:第20幅图是什么动作?他想了一会儿,回答与第二幅图相同,又要笔者出更难的题目。再出了个61,他回到座位上,写写、画画,也正确地解决了问题。
笔者接着问他第88幅、第123幅、第800幅分别是什么动作。虽然他探索的时间都较长,但在耐心等待下,除第123幅图的动作错了,其他都对。
他是怎么探索的?首先在探索的过程中找到整十、整百时图形的变化规律,再从最接近的整十、整百开始快速解决问题。如10、20、30分别与1、2、3的动作一样,100、200、300也分别与1、2、3的动作相同。找到了1到9的动作变化规律,就找到了10到90及100到900的变化规律。
实际上他在头脑里创造了一张“3的倍数”(虽然他并不知3的倍数)与余数模型图,如同一张数的网格图(如图3,笔者依据该学生的描述所画),再在头脑里运用这个模型图快速检索得到答案。
如883,先从880开始确定与第一幅图的动作一样,则881、882幅图分别对应的是第二、三两幅图,这样依次重复下去。
笔者惊叹他的创新性思维,也暗暗庆幸自己不暗示、不提示,让他有充分的自由探索时间,才开出如此美丽的创新之花。
(二)留足学生自由展示的时间
展示学生的探索成果,有利于学生之间开展有针对性的自由争论,从而激发学生的学习兴趣,进而借鉴同伴间解决问题的创新性方法与过程,提高学习成效。
如教学人教版二年级上册“乘法初步认识”时,课后练习有这样一道题:endprint
“请任意写一道乘法算式,并画图表示所写乘法算式的意思。”在学生自由写乘法算式、画乘法意义后,笔者留足展示学生作品的时间,课上出现了许多精彩的想法。
生:我写的乘法算式是“4×5=20”,我先一行画了4个圆圈,画了5行,表示5个4的和是20;也可以理解成一竖(列)有5个,有4竖(列),表示4个5的和是20。
生:我写的乘法算式是“9×9=81”,我是结合买玩具来理解的,我买跳跳球,一个9元钱,我买了9个,要付的钱是9个9元。
生:我寫的乘法算式是“1×1=1”,我是用圆圈表示的,就在本子上画出1个圆圈就行了,最简单,表示1个1是1。
生:我是用叉叉表示的,一行先画几个叉叉,在中间用省略号表示,我就表示100个叉叉;再竖着也用省略号表示,表示100行,这个算式的意思是有100个100。也可以这样想,这个叉表示一种外星文字,一行是100个,有100行,一共有100个100等于10000个外星文。所以算式是“100×100=10000”。
生:我这个最有趣了,我是在这个方框内用圆圈表示0×0=0,你看到了什么吗?一个都没有,就表示0个0。
生:我表示的算式是0×3=0,今天3个人想吃大饼,每人0个大饼,这3个人共吃了3个0,还是0个大饼。
生:我写的算式是X×X=X,我的图有无数种画法,因为X可以代表3、代表0,也可以代表100,也就是不管代表什么数都可以的意思。所以我这个算式把你们刚才画的图与意思都包括在里面了。
……
因为留足了学生自由展示的时间,每个学生都有机会将自己个性化的想法展示出来。展示的过程既是建立乘法意义直观模型的过程,也是展示自己独特个性的过程。这样的过程有利于激发学生的学习兴趣,唤醒学生标新立异的创新性思维,这对培养学生的创新意识很有好处。
三、创“自由探索”空间,结创新之果
培养创新意识,除了有效的激励措施,充分的探索时间,还需要创设“自由探索”的空间,让学生能在富有弹性的自由探索的空间内产生个性化的解决方法,从而体会到创新之快乐。要做到这点,就要依赖教师所设计的开放性学习材料,主要有两点。
(一)呈现选择性探索材料,让学生有自由选择的机会
尊重学生的自由选择权能激发学生的探索动力,进而促进学生去主动创新。而尊重学生的选择权,首先教师必须要提供让学生有选择机会的开放性、富有弹性的学习材料,学生再结合自身的学习能力、知识基础选择适合自己探索的材料开展研究。
例如三角形内角和的教学,笔者是这样进行的。
(1)师生交流学法。课始通过师生交流,了解到运用与新课相关的旧知识通过转化的方法学习新知,是常用的学习方法。
(2)揭示学习内容“三角形的内角和”,并指出三角形内角和分别所在位置与意思。讨论与本课新知有关的旧知识分别有哪些,共同推测可能有如下相关知识:用量角器量角、特殊角度数(平角180°,直角90°,周角360°)、长方形内角和90°×4=360°。
(3)呈现材料。
材料一:呈现锐角三角形、直角三角形、钝角三角形等图形各一个。
材料二:呈现锐角三角形、直角三角形、钝角三角形纸片若干个。
(4)选择材料和探索方法。
任选两组材料中的一个或几个三角形,再任选所运用的一种或两种旧知识探索其内角和。
(5)学生自由探索(过程略)。
在上例中,学生探索的材料是自己选择的,探索的方法也是自己选择的,因为选择,所以喜欢,因为喜欢才使学生的探索富有成效,有通过量内角和解决问题的,也有拼成长方形研究直角三角形内角和的,还有把三个内容拼成平角研究内角和的……每位学生都有了自己独特的创造性的想法,课堂也结满了创新之果。
(二)呈现本源性探索材料,让学生有自由思维的空间
促进学生学习的材料主要有两类。一是基于包含其前位知识的带有暗示探索过程的学习材料,这种学习材料主要指向于学生新知的获得(详见下例材料一)。优点是知识掌握得较扎实,不足的是学生的思维空间较小,往往按材料的暗示方向进行探索。另一类直达新知识本源的不暗示、富有想象空间的学习材料,其能使学生在探索中有充分的自由思维的时间与空间(详见下例材料二)。学生学习主动性较高,思维的挑战性更强,易激发学生的创新欲望,易出现富有创新性的探索结果。
例如,人教版五年级“三角形的面积”两种不同的学习材料。
1.暗示性的材料。
材料一及简要过程:
(2)将上图沿一条对角线平均分成两个三角形,求阴影部分的面积(如图5)。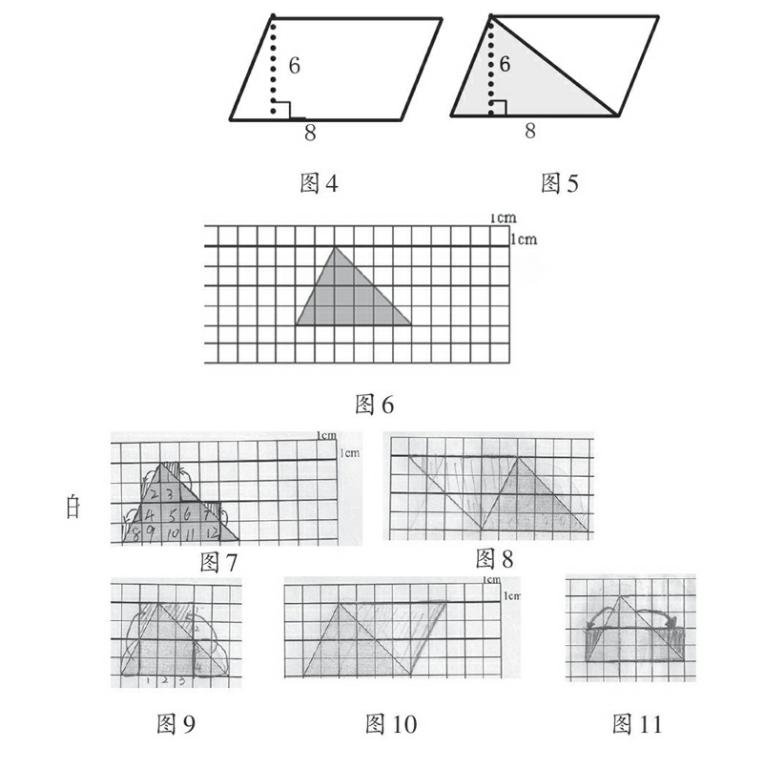
(3)对三角形面积计算方法进行猜测,再验证。(过程略)
学生能证明三角形面积的计算,但都是用两个全等三角形拼成平行四边形的方法,结果较单一。
2.本源性的材料。
材料二及简要过程:
(1)呈现如图6材料,让学生想办法得到三角形的面积,再将自己的想法画出来,使别人能一眼看出他们的想法。
(2)学生独立画图,再展示思维过程,介绍自己的想法。具体如图7~11所示。
(3)学生猜测三角形面积计算方式及验证。(过程略)
从上例的探索过程与结果可以看出,我们把三角形的面积放到面积单位这一知识的源头,打开了学生自由思维的空间,学生的探索过程不再单一,个性化想法非常丰富。
总之,在小学数学课堂上发展学生的创新意识是一个长期的、复杂的过程。学生创新意识的发展是一个由多种因素综合起作用的整体性过程。既需要有自由探索的良好氛围、充足时间及空间,还需要学生具有广博的知识面,不畏艰险、勇于探索的精神,更需要学生具有善于提出问题、发现问题的能力。因此,培养学生的创新意识,我们还有许多问题要解决,还有许多做法有待研究。
参考文献:
[1]曹培英.跨越断层,走出误区“数学课程标准”核心词的实践解读之十——创新意识[M].上海:上海教育出版社,2015.
[2]陈选峰.基于“学”的课本材料有效的开发与实践[J].教学月刊·小学版(数学),2014(6).
(浙江省临海市邵家渡中心校 317000)endprint
