需求不确定条件下生鲜农产品供应链网络设计

赵广华，刘佳怡

（浙江财经大学 工商管理学院，浙江 杭州 310018）

需求不确定条件下生鲜农产品供应链网络设计

赵广华，刘佳怡

（浙江财经大学 工商管理学院，浙江 杭州 310018）

生鲜农产品具有易腐性、易损性，与传统的供应链相比，生鲜农产品供应链在运输过程中会产生损耗成本。研究了消费者需求不确定情况下的由供应商、产地物流中心、销地配送中心、零售商组成的单一产品、单一产地物流中心供应链网络，运用模糊数学相关理论将不确定模型转化为确定型模型，并引入实例用Lingo求解。

不确定需求；生鲜农产品；供应链网络；供应链网络设计

1 研究现状

国内外对生鲜农产品供应链的研究大多是关于供应链的协调与优化，在需求不确定条件下供应链网络设计优化方面，则主要是通过建立相关模型，然后引入实例并进行求解。

1.1 生鲜农产品供应链的协调与优化

Guohua S（2013）研究基于一个供应商和一个零售商的供应链模式，建立了生鲜农产品供应链的动态模型，通过价格来协调供应链的利润，并用算例验证其有效性。Cai X,Chen J,Xiao Y（2012）在生鲜农产品供应链中研究了物流外包的情况，通过两个协调契约来引导各供应链成员之间进行有效合作。吴丹（2014）探讨了电子商务环境下生鲜农产品供应链协调问题，主要包括了三部分：节点企业的协调、3PL企业的配送协调、信息的协调，并提出了相应的优化方法。林梦楠（2015）在考虑生鲜农产品的协调与优化时引入协调契约，并引入算例得出结论：该契约能够实现供应链的协调，使供应链各方都获益。

1.2 需求不确定条件下供应链网络设计

Cardona-Valdés Y（2011）分析了不确定条件下的供应链网络设计问题，建立了随机需求下的优化模型，采用两级整数规划模型对其求解。Pishvaee M S（2011）探讨了不确定条件下的闭环供应链网络设计问题，运用鲁棒优化理论提供了一个框架来处理优化问题中参数的不确定性，建立了闭环供应链网络设计问题中客户需求不确定的鲁棒优化模型，并对模型求解中得到的多个解决方案进行比较。夏盛盛（2011）探讨了制造企业的供应链网络设计问题，考虑市场的不确定性，建立模糊模型并转变为确定型，引入实例并用Matlab对模型求解。屠丹（2014）用模糊参数表示客户的不确定需求，考虑生鲜农产品在运输过程中的损耗成本，建立含有模糊参数的优化模型，并转化为确定型，运用Matlab和Lingo求解。

2 供应链网络设计的理论基础

2.1 农产品供应链的概念

对于农产品供应链的定义，不同的学者有不同的理解，Downey（1996）认为农产品供应链是从农产品生产者开始，经过生产、加工、零售等过程，最后与消费者连接的网络系统。本文的生鲜农产品供应链参考了Downey的看法，研究的是基于农产品供应商、物流商、分销商以及零售商形成的网络。

2.2 模糊集合理论

模糊集合理论由Zadeh在1965年提出，对于给定的论域，其中的一个模糊集A是指对任何x∈X，都指定了μA(x)∈[0,1]与X对应，称为x对于A的隶属度，这意味着做了一个映射：

这个映射称为A的隶属函数。

本文研究中用的是三角模糊数为（a,b,c），其隶属函数为：

3 不确定需求下生鲜农产品供应链网络设计

由于生鲜农产品具有易腐性、易损性，与传统的供应链相比，生鲜农产品供应链对时间的敏感性较强，在运输过程中也会产生较高的损耗成本。生鲜农产品具有季节性特征，面向的消费者也较为分散，需求也有较大的不确定性，因此本文在不确定需求条件下，对由生鲜农产品供应商、产地物流中心、销地配送中心、零售商组成的供应链进行研究。由于单个消费者的需求较为分散，因此，本文把单个客户的需求反映到零售商上，考虑零售商需求的不确定性。在研究过程中，考虑只有一种生鲜农产品和只有一个产地物流中心的情况，解决是否应该建设销地配送中心以及各个节点之间生鲜农产品的配送数量问题，来进行供应链网络设计。

3.1 生鲜损耗系数的确定

生鲜农产品的新鲜度随着时间的延长而下降，相应的，其价值也随着新鲜度的下降而降低，本文采用张多（2009）所构建的指数函数来描述新鲜损耗系数，定义如下:

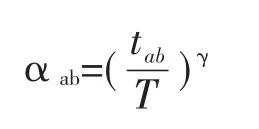
αab表示生鲜损耗系数，tab表示生鲜农产品的运输时间，γ表示时间敏感因子，T表示生鲜农产品的保质期，tab＜T，当tab=T时，αab=0。

3.2 模型的建立

3.2.1 模型假设

（1）供应链网络中供应商、产地物流中心、销地配送中心的需求不能超过最大容纳能力，且供应商的供应能力、物流中心和销地配送中心的配送能力都为确定值。

（2）零售商之间对于生鲜农产品的需求是互不影响的。

（3）待选的销地配送中心的位置和个数已知。

（4）总运输成本与运输所花费的时间和运输量成正比。

（5）备选的销地配送中心固定成本和运营成本已知。

（6）单位时间单位生鲜农产品运费已知。

（7）每个零售商只能接受一个销地配送中心的配送。

3.2.2 符号说明

（1）集合

s:生鲜农产品供应商的编号；S:生鲜农产品供应商的集合，s∈S；

m:产地物流中心的编号，在本文中m=1，M：产地物流中心的集合，m∈M；

i:销地配送中心的编号，I：销地配送中心的集合,i∈I；

j:零售商的编号，J：零售商的集合，j∈J。

（2）决策变量

ai：是否选择开办第i个销地配送中心，如果开办，ai=1，否则为0；

bij：销地配送中心I能否给零售商J供货，如果可以供货，bij=1，否则为0；

qsm：供应商S供给产地物流中心M的生鲜农产品数量；

qmi：产地物流中心M配送给销地配送中心I的生鲜农产品数量；

qij：销地配送中心I分销给零售商J的生鲜农产品数量。

（3）常量

cs：供应商S供应生鲜农产品的最大数量；

wi：销地配送中心的分销能力上限；

w：准备建设的销地配送中心的最大数量；

d͂j：零售商对生鲜农产品的模糊需求；

αab：生鲜农产品损耗系数；

p：供应商S供应生鲜农产品的单位成本；

hm：流经产地物流中心M的单位运营成本；

ki：建立销地配送中心I的固定成本；

li：经过销地配送中心I的单位运营成本；

rsm：供应商S到产地物流中心M的单位时间单位农产品的运输费用；

rmi：产地物流中心M到销地配送中心I的单位时间单位农产品的运输费用；

rij：销地配送中心I到零售商J的单位时间单位农产品的运输费用；

tsm：供应商S到产地物流中心M的运输时间；

tmi：产地物流中心M到销地配送中心I的运输时间；

tij：销地配送中心I到零售商J的运输时间；

αsm:供应商S到产地物流中心M的新鲜度损耗系数，

αmi：产地物流中心M到销地配送中心I的新鲜度损耗系数，

αij：销地配送中心I到零售商J的新鲜度损耗系数，

3.2.3 以成本最小化来建立模型1

目标函数：

约束条件：

目标函数为成本最小化，成本包括供应商的供应成本、产地物流中心的运营成本、销地配送中心的固定成本与建设成本、各节点之间的运输成本与损耗成本。

约束条件：式（1）表示供应商的供应能力小于其可以供应的最大数量；式（2）表示产地物流中心的配送能力限制；式（3）表示开办的销地配送中心的数量限制；式（4）表示一个零售商只能由一个销地配送中心来配送商品；式（5）表示产地物流中心只针对选中的销地配送中心来进行产品的配送；式（6）表示各节点之间的农产品的流通数量相等；式（7）表示生鲜农产品的配送时间小于其保质期；式（8）表示只有销地配送中心进行建设，才能给零售商提供农产品；式（9）表示销地配送中心分销给零售商的生鲜农产品的数量等于其从产地物流中心收到的数量；式（10）表示是否选择开办第i个销地配送中心，如果开办，ai=1，否则为0；式（11）表示各节点之间的配送数量均大于等于0。

3.3 模型的转换

上面建立的模型中，在目标函数与约束条件中都包含有不确定参数，很难进行求解，因此根据模糊数理论中的模糊机会约束规划，将含有模糊数的模型转化为确定模型。根据刘宝碇（2003）提出的理论来定义含有模糊参数的单目标机会约束规划模型：

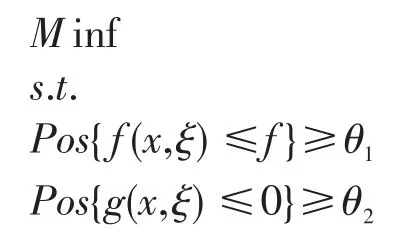
在模型中，x是决策变量，ξ是模糊参数变量，f(x,ξ)是含有模糊参数的目标函数，g(x,ξ)是含有模糊参数的约束条件，Pos{·}表示的是大括号中事件成立的可能性，θ1是目标函数的置信水平，θ2是约束条件的置信水平，由决策者事先决定。

将上述含有模糊参数的供应链网络模型进行转化，得到模型2：Minf

模型2中的目标机会约束表示在使供应链成本尽量最小时，置信水平至少为θ1，同样，约束条件的机会约束表示在使销地配送中心配送给零售商的生鲜农产品等于客户需求时，置信水平至少为θ2，模型2中的其他约束条件与模型1相同。

现在是对含模糊参数的单目标机会约束规划模型求解，本文先把模糊约束和目标函数转化为清晰等价的确定模型，然后再进行求解。根据模糊数与模糊数͂的可能性定义，当͂为清晰数b时，有：

（1）模糊目标约束的转换。对模糊目标约束式转化，假定各零售点的需求d͂j均为三角模糊数，表示为（dj1,dj2,dj3），dj1＜dj2＜dj3，令：

依据模糊数的四则运算法则，模型2中的左边表达式可变为如下形式：

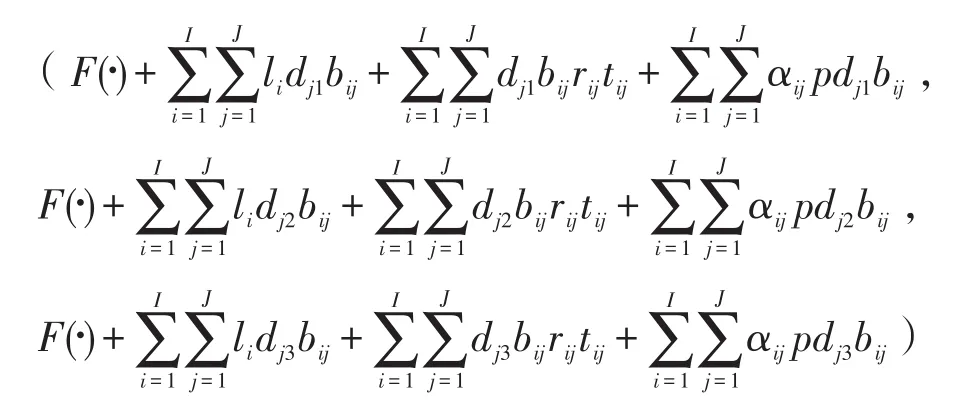
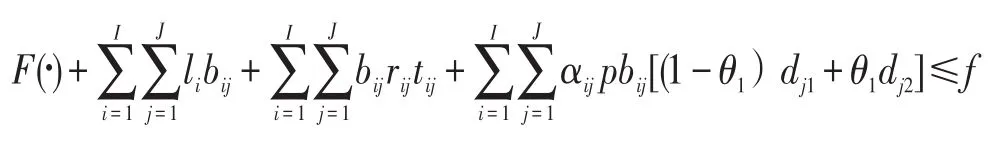
简化后可得到：

（2）模糊约束条件的转换。同理，对模糊约束条件也进行转化，对于零售商的模糊需求，以（dj1,dj2,dj3）表示，dj1≤dj2≤dj3，因此可以表示为（dj1bij,dj2bij,dj3bij）。设三角模糊数͂为（a1,a2,a3）,隶属函数为μa͂(x)，对于给定的置信水平θ2（0≤θ2≤1）,当且仅当时，有成立，所以可以转化为：

最后得到的模型和模型1相比，除了对模糊目标约束和模糊约束条件进行转换外，其余约束条件都相同，这里不再赘述。

4 案例分析

某生鲜农产品企业因业务拓展需要，在其主要销售地开设销地配送中心，在供应链网络中，共有5家供应商、1个产地物流中心、5个待选销地配送中心、8家零售商。要在待选的销地配送中心中最多选择3家进行分销，目标函数的置信水平为0.9，约束条件的置信水平为0.8，时间敏感因子γ=0.85，产品的保质期为30天，单位成本为0.2万元/t，农产品在产品配送中心的单位时间单位产品的配送费用为0.001 8万元/t·月，分销中心至零售商的单位时间单位产品的运费为0.002 4万元/t·天。其他相关数据见表1-表7。

表1 每个供应商对该产品的供应能力cs、建设销地配送中心的固定成本ki、单位产品的运营成本li、配送能力上限wi，单位：t/月，万元/月，万元/t·月，t/月

表2 最终客户的模糊需求

表2 最终客户的模糊需求

1（25,30,35）5（100,105,110）2（65,70,75）6（60,65,70）3（70,75,80）7（40,45,50）4（90,95,100）8（60,65,70）

表3 供应商到产地物流中心的单位时间单位产品的运费rsm,最短运输时间tsm，单位：万元/t·天，天。

表4 产地物流中心到销地配送中心的单位时间单位产品的运费rmi,最短运输时间tmi，单位：万元/t·天，天

表5 待选销地配送中心到最终客户的最短运输时间tij,单位：天

表6 供应商到产地物流中心的生鲜损耗系数αsm,产地物流中心到销地配送中心的生鲜损耗系数αmi

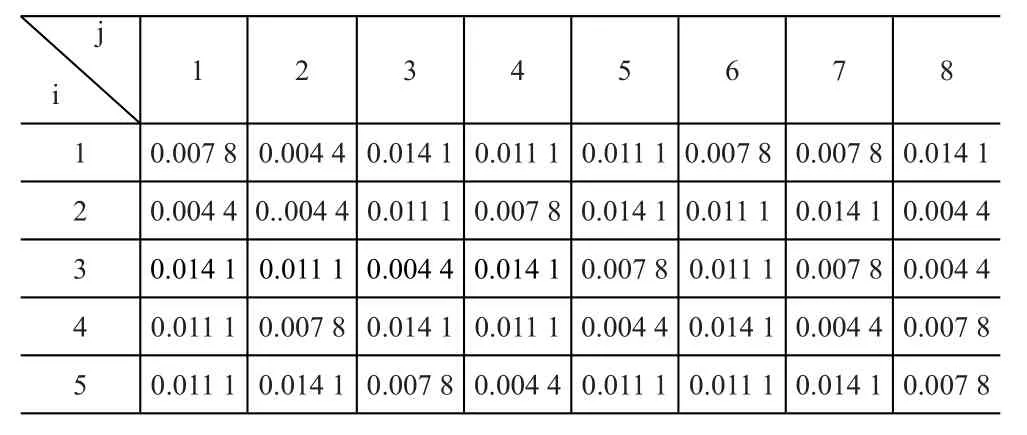
表7 待选销地配送中心到零售商的生鲜损耗系数αij

将已知的系数代入模型，运用Lingo11.0来求解，可得到如下结果：

在5个待选销地配送中心中，选择3、4来进行建设，销地配送中心3可以向零售商1、4、5、7、8配送，配送量分别为29、94、104、44、64，销地配送中心4可以向零售商2、3、6配送，配送量分别为69、74、64，供应商向产地物流中心配送的数量依次为132，100，120，100，90，产地物流中心配送给销地配送中心的数量q12=335，q13=207。得出的供应链网络总成本为441.833元/月。

5 结论

本文研究了需求不确定条件下的生鲜农产品供应链网络设计问题，考虑了生鲜农产品在运输过程中会产生的损耗成本，运用三角模糊数来表示不确定需求，以供应链成本最小化来对供应链网络进行规划设计，引入实例后运用Lingo进行求解，能帮助企业在需求不确定条件下进行生鲜农产品供应链设计和决策。

[1]Cai X,Chen J,Xiao Y,et al.Fresh-product supply chain management with logistics outsourcing[J].Omega,2013,41(4):752-765.

[2]Guohua S.Research on The Fresh Agricultural Product Supply Chain Coordination with Supply Disruptions[J].Discrete Dynamics in Nature and Society,2013,(13):1-9.

[3]吴丹.电子商务生鲜农产品供应链协调机制研究[D].武汉:武汉轻工大学,2014.

[4]林梦楠.生鲜农产品供应链协调性研究[D].秦皇岛:燕山大学,2015.

[5]Cardona-Valdés Y,lvarez A,Ozdemir D.A bi-objective supply chain design problem with uncertainty[J].Transportation Research Part C Emerging Technologies,2011,19(5):821-832.

[6]Pishvaee M S,Rabbani M,Torabi S A.A robust optimization approach to closed-loop supply chain network design under uncertainty[J].Applied Mathematical Modelling,2011,35(2):637-649.

[7]夏盛盛.不确定需求下供应链网络设计研究[D].哈尔滨:哈尔滨商业大学,2011.

[8]屠丹.不确定需求条件下农产品供应链网络优化问题研究[D].厦门:集美大学,2014.

[9]张多.农产品供应链的网络设计[D].南昌:华东交通大学,2009.

[10]刘宝碇.不确定规划及应用[M].北京:清华大学出版社,2003.

Design of Fresh Farm Produce Supply Chain Network with Demand Uncertainty

Zhao Guanghua,Liu Jiayi
(School of Business Administration,Zhejiang University of Finance&Economics,Hangzhou 310018,China)

In this paper,we studied the supply chain network which included a single place of origin logistics center,multiple suppliers,place of destination distribution centers and retailers for a single product with uncertain consumer demand,used the fuzzy theory to convert the uncertainty model into a deterministic model and used the Lingo software to solve the model in connection withan empiricalcase.

uncertain demand;fresh farm produce;supply chain network;supply chain network design

F274;F762

A

1005-152X(2017)10-0109-05

10.3969/j.issn.1005-152X.2017.10.022

2017-09-10

浙江自然科学基金项目（LY17G020017）

赵广华（1960-），男，河南许昌人，浙江财经大学现代物流经济研究所所长，工商管理学院教授，博士,主要研究方向：物流与供应链管理；刘佳怡（1993-），女，浙江嵊州人，浙江财经大学工商管理学院2015级研究生，研究方向：物流与供应链管理。