基于禁忌搜索和Floyd 混合算法的物流配送路线规划

乔仁杰，周思育，田 琪，宋庭新

（湖北工业大学 机械工程学院，湖北 武汉 430068）

基于禁忌搜索和Floyd 混合算法的物流配送路线规划

乔仁杰，周思育，田 琪，宋庭新

（湖北工业大学 机械工程学院，湖北 武汉 430068）

以某医药集团湖北配送业务为背景，采用禁忌搜索算法对药品物流配送路线进行了规划，在此基础上运用Floyd算法对规划的路线进行路网匹配，生成与配送区域实际道路相吻合的最优路径。实际应用表明，经过这种混合算法生成的行车路线不仅与实际道路相匹配，而且大大减少了车辆行驶里程，节约了燃油和物流成本，在物流运输领域具有良好的经济和社会价值。

配送路线规划；禁忌搜索算法；Floyd算法；物流

1 引言

物流路径优化问题最早是由Dantzig和Ramser在1959年提出的，即所谓的车辆调度问题（Vehicle Routing Problem，VRP）[1]。车辆调度问题的理论涉及多学科，很多实际问题都可以归于这一类问题，应用前景广阔，所以成为运筹学与组合优化领域的研究热点。近几十年来，对车辆优化调度问题的研究取得了很多有意义的成果，已经广泛应用于生产、生活的各个方面。随着经济发展，物流行业对社会的影响日益显著，而配送是物流行业中的重要环节，配送路线的设计和选择对物流公司的运输成本以及货物的运输效率有着重要影响，因此选择一条合理的配送路线是物流运输中需要研究的重要问题[2]。

本文运用物流工程相关知识，以某医药集团医药物流配送路线规划问题为背景，选择禁忌搜索和Floyd混合算法作为物流网络模型优化算法，提出一种解决物流配送路线规划的方案，寻求最优配送路径，以达到提高物流效率和降低运输成本的目的。

2 车辆配送路径优化算法

车辆配送路径优化是NP-hard问题，使用的方法一般分为两大类[3]：一类是精确搜索非精确解的方法，如C-W节约算法与禁忌搜索算法；一类为启发式搜索方法，如ANT蚁群算法、AN模拟退火算法。其中，禁忌搜索算法是一种全局逐步寻优算法，它通过引入灵活的存储结构和相应的禁忌准则来避免迂回搜索，并通过藐视准则来赦免一些被禁忌的优良状态，进而保证多样化的有效探索，以最终实现全局优化。禁忌搜索算法比较直观，算法简单，可以回避局部临域搜索陷入局部最优的不足，克服其它算法爬山能力差的缺点，从而加快收敛速度，提高了解的质量，也能够满足运行路线和时间安排原则[4]。而在求解最短路线中，启发式搜索算法与禁忌搜索算法相比准确度不够，过程较为繁琐，所以本文选择禁忌搜索算法来求解最优车辆配送路径。

2.1 禁忌搜索算法

首先，给定一个初始解和一种邻域，然后在当前解的邻域中确定若干候选解；若最佳候选解对应的目标值优于“best so far”状态，则忽视其紧急特征，用其代替当前解和“best so far”状态，并将相应的对象加入禁忌表，同时修改禁忌表中各对象的任期；若不存在上述候选解，则在候选解中选择非禁忌的最佳状态为新的当前解，而无视它与当前解的优劣，同时将相应的对象加入禁忌表，并修改禁忌表中各对象的任期。如此重复上述迭代搜索过程，直至满足停止准则。其算法步骤具体为：

（1）选定一个初始解xnow，置禁忌表H=∅。

（2）若满足终止规则，则终止计算；否则，在xnow的邻域N(H,xnow)中选出满足禁忌要求的候选集Can_N(xnow),在Can_N(xnow)中选一个评价值最佳的解xnext,令xnow=xnext，更新历史记录H，重复（2）。

禁忌搜索算法的流程如图1所示。

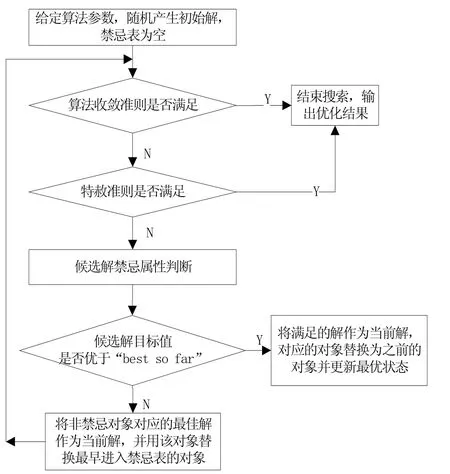
图1 禁忌搜索算法流程图

2.2 Floyd算法

运用禁忌搜索算法求解之后，虽然求出了经过所有配送点的最短直线距离，但与能够行走的实际路网并不匹配，需要结合实际路网把直线最短路线还原为实际路线，这里便需采用Floyd算法。Floyd算法是一种寻找给定的加权图中顶点间最短路径的算法，此算法可用来求解两点间的实际最短路线，其基本思路是在两个配送点之间根据实际路网插入若干中间节点，然后求解经过这些中间节点的最短路线[5]。具体算法如下：

（1）首先根据模型中的点构建一个邻接矩阵A0，A0是对称矩阵，即，然后取初值

（3）递推产生一个矩阵序列A0,A1，...,An(1≤k≤n)。

（4）当k=n时，就得到了最短路径，即矩阵An就是各顶点间的最短路径值，否则令k=k+1(k是迭代次数)，转第（2）步。

3 案例分析

3.1 背景介绍

为验证上述算法的有效性，本文选取某医药集团在武汉市东西湖区常青花园一带的配送点进行建模。文中使用的配送点是依据该集团LMIS系统中导出的2016年4月份湖北运输部的配送数据。东西湖区2016年4月的配送点有54个（如图2所示），在调查过程中发现常青花园一带配送量大，每次配送点多且集中，配送时可进行协商，将部分连锁药店的配送工作转交给药店内部调配，从而减少同一个区域的配送点。由于每次配送的地点是根据订单临时生成的，因此随机选取了10个配送点进行线路优化，如图2中圆圈所示。

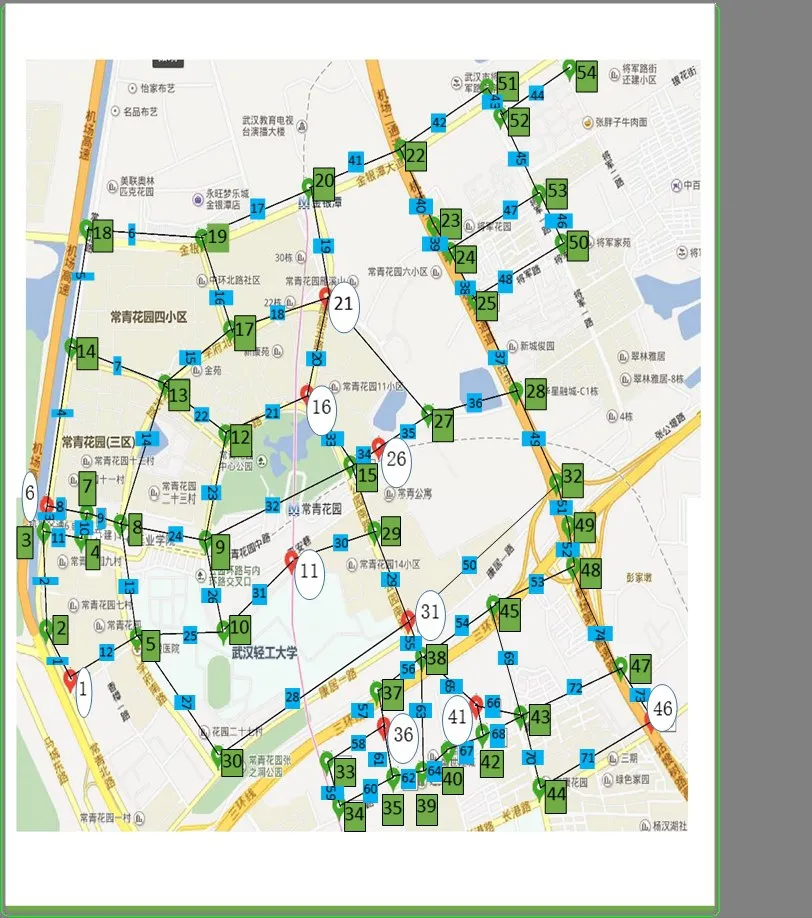
图2 武汉市东西湖区常青花园附近路网及配送点

3.2 用禁忌搜索算法求解最短路线

使用MatLab软件编程调用禁忌搜索算法程序。在MatLab中，取已选定的10个点（图2中圆圈所示，后同），在代码中把索取到的点1、6、11、16、21、26、31、36、41、46，依次重新编号为1、2、3、4、5、6、7、8、9、10，进行禁忌搜索计算后，得到巡回序列以及巡回距离，见表1。

从表1可知，求得的最短巡回距离为357.189 9km，由于起始点分别从3、4、5、6、7、8、9、10的巡回序列所走的巡回路径是一样的，且巡回路径重复多次，说明所求路径正是这些重复的路径，因此用禁忌搜索算法取得的最短路径为3-8-9-10-7-6-4-5-2-1-3，还原到地图中的点为11-36-41-46-31-26-16-21-6-1-11，将这些点还原到地图，依次连接得到路线如图3所示。

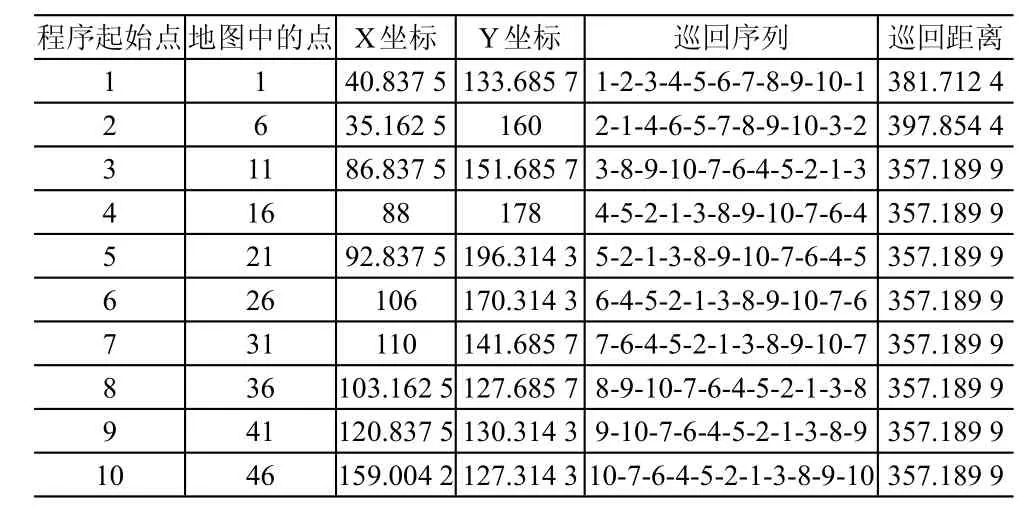
表1 通过Matlab计算得到的巡回路线以及巡回距离

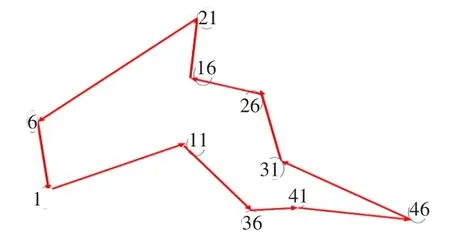
图3 还原到地图的最短路线

图3所示的最短路线是各配送点直接相连得到的路线，与实际路网并不匹配，因此还需要使用Floyd算法对该路线进一步进行规划。具体方法是根据实际路网，在相邻两配送点之间的实际道路上选取关键节点重新构建两点之间的最短路线。

3.3 使用Floyd算法构建最短路线矩阵

取配送点6-21为例构建邻接矩阵。根据地图中实际路网的分布，需要在6-21之间插入四个关键节点7，8，13，17，如图4所示。构建的邻接矩阵如图5所示。

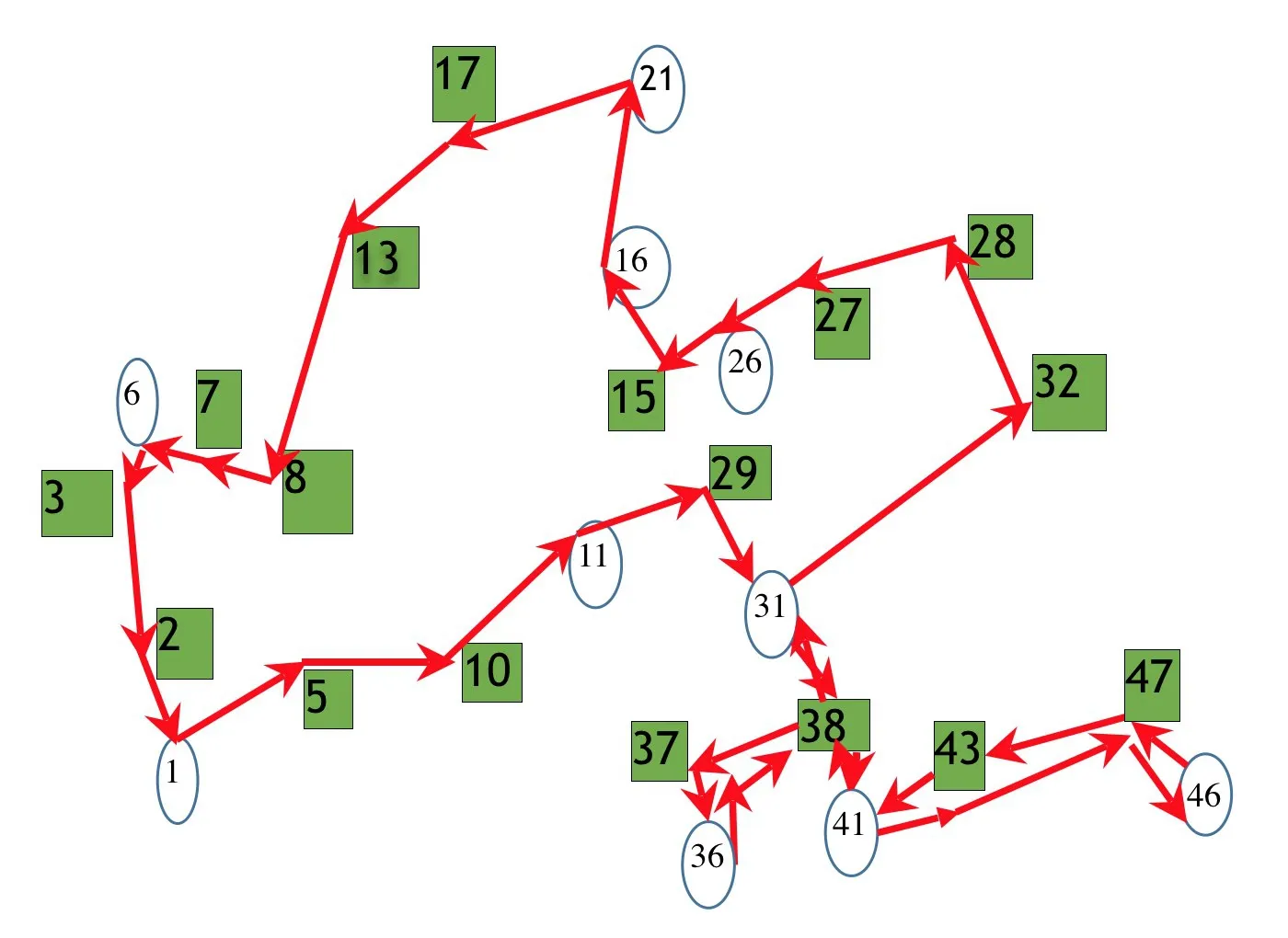
图4 还原路网后的实际路线

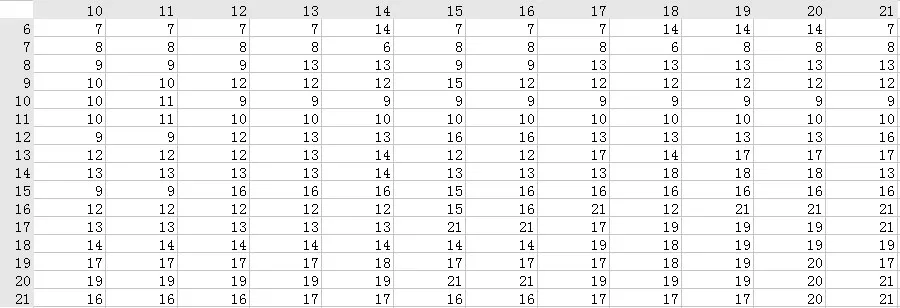
图5 邻接矩阵

上述邻接矩阵的意义是：程序点中点6到点21的最短路线是这样得到的，第6行第21列为7，第7行第21列为8，第8行第21列为13，第13行第21列为17，第17行第21列为21，则点6到点21的最短路线是6-7-8-13-17-21。

3.4 通过Floyd算法计算后的最短路线

在MatLab中编程调用Floyd算法程序，根据邻接矩阵求出两点之间的最短路线以及距离，并将距离相加求得距离之和，见表2。

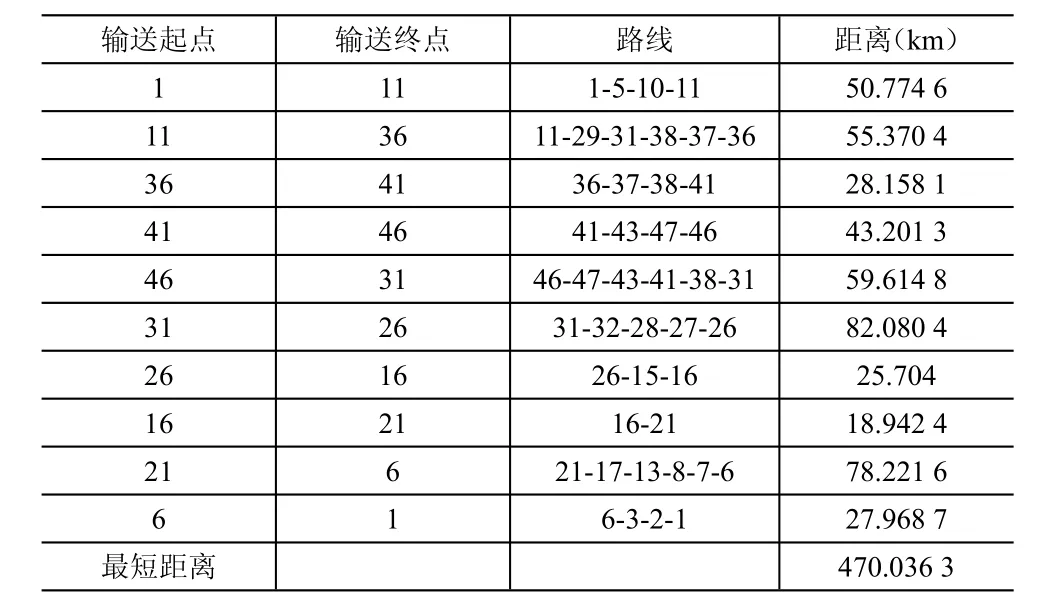
表2 通过Floyd计算得到的最短路线及最短距离

根据表2得到的数据以及路线关系还原路网后的实际路线如图4所示。

3.5 基于Floyd算法的路线优化

在Floyd算法中，在上一次计算完成后，下次运算就剔出已经经过的配送点。例如本模型中，从11-36，按照Floyd算法路线是11-29-31-38-37-36；从46-31，按照Floyd算法路线是46-47-43-41-38-31。但是显然在11-36时已经经过了点31，故Floyd算法在计算46-26时将剔出点31，这样就会形成一个比较好的串连路线46-47-48-49-32-28-27-26。故优化后的最短总距离为：D=50.774 6+55.370 4+28.158 1+43.201 3+92.000 0+25.704 0+18.942 4+78.221 6+27.968 7=420.341 1。优化后的实际线路如图6所示。

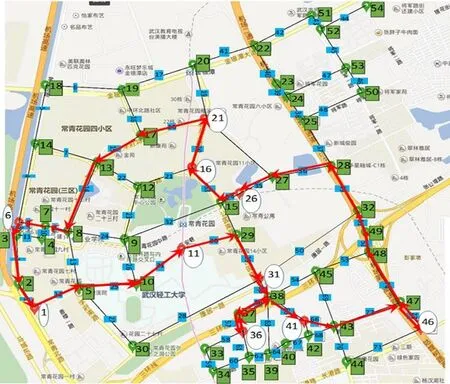
图6 优化后的实际路线

3.6 路线优化后的物流成本核算

优化后的最短总距离D=420.341 1，所用地图比例是1：23，故实际里程为D=420.341 1×23/1 000=10.2km。根据LMIS系统中的数据，该月使用依维柯车型配送的次数是46次，日均配送次数1.5次，配送行驶里程为3 288km，平均每次配送行驶73.07km，由于该医药物流配送中心设在汉阳，汉阳到所取模型区域配送行驶里程不会超过30km，也就是说按照路线优化后的配送路线进行配送可减少行驶公里数为S=73.07-30-10.2=32.87km。假设依维柯汽车每百公里平均耗油为8L，则路线优化后每辆车每个区每次配送可节省燃油升数为l=32.87×0.08=2.63 L。每天上午和下午各配送一次则一天省油L=l×2=5.26L，第一季度节省燃油L1=L×（31+28+31）=473.4L，第二季度节省L2=L×（30+31+30）=478.66L，第三季度节省L3=L×（31+31+30）=483.92L，第四季度节省L4=L×（31+30+31）=483.92L，则一年节省的油费约为（473.4+478.66+483.92+483.92）×5.7=10 934.43元，即一辆车一年节省的燃油费约为1万元。该公司在武汉地区投入的配送车辆有24辆，因此仅武汉地区一年节约的燃油费用就达到24万元。

4 结语

本文结合禁忌搜索算法与Floyd算法来规划物流配送路线，先利用禁忌搜索算法规划理想最短路线，再结合Floyd算法与实际网路的情况将理想最短路线还原为实际路线，最终得到具有实际意义的物流配送优化路线。本方案在该医药集团公司自实施至2016年9月底，效果显著，公司物流成本明显降低，配送效率得到明显提升。因此，本文提出的路线规划算法理论具有良好的实际运用效果，可显著提升物流配送效率。

[1]Cheng Guoniang,Zhuang Zhenquan.Theory and Application of the Genetic Algorithm[M].Posts&Telecom Press,1999.

[2]尚华艳.物流配送中车辆路径问题研究[D].武汉:武汉理工大学,2005.

[3]康晓军,王茂才.基于遗传算法的最短路径问题求解[J].计算机工程与应用,2008,44(23):22-23.

[4]曹立斌,周建兰.一种改进的禁忌搜索法在函数优化问题中的应用[J].计算机技术与发展,2003,13(a02):39-42.

[5]樊蓉.物流配送中车辆调度算法的比较研究[D].南京:南京农业大学,2013.

Planning of Logistics Distribution Route Based on Tabu Search and Floyd Algorithm

Qiao Renjie,Zhou Siyu,Tian Qi,Song Tingxin
(School of Mechanical Engineering,Hubei University of Technology,Wuhan 430068,China)

In this paper,we applied the tabu search algorithm to the routing of the medicine logistics distribution business of a certain pharmaceutical group in Hubei;then on such basis,we iused the Floyd algorithm for the road network matching of the planned route to yield the optimal route that fitted most closely with the actual road condition of the distribution area;and at last,through a practical application,we demonstrated the economic and social value of the hybrid algorithm proposed in this paper.

distribution route planning;tabu search algorithm;Floyd algorithm;logistics

F224.0;F252.14

A

1005-152X(2017)10-0083-04

10.3969/j.issn.1005-152X.2017.10.017

2017-08-01

湖北省交通运输厅科技项目（鄂交科教2016-600-5-3）；国家级大学生创新创业训练计划项目（201610500037）

乔仁杰（1994-），男，湖北宜昌人，硕士研究生，研究方向：工业工程；宋庭新（1972-），男，湖北宜都人，教授，研究方向：工业工程。