基于混合差分遗传算法的聚类车辆路径问题研究

朱 颢

（湖州职业技术学院，浙江 湖州 313000）

基于混合差分遗传算法的聚类车辆路径问题研究

朱 颢

（湖州职业技术学院，浙江 湖州 313000）

针对所有客户被预先分配给若干聚类的聚类车辆路径问题，建立了相应的整数规划模型，提出基于差分进化和遗传算法的两级混合算法。在聚类层，运用差分进化算法进行优化，染色体基于聚类编号进行编码，采用扫描算法初始化种群，结合聚类层的编码特点，设计了基于升序排列的变异算子，在交叉环节考虑传统差分进化算法的缺陷，设计了考虑聚类服务数和装载率的混合交叉算子；在客户层，运用遗传算法进行优化，染色体基于客户编号进行编码，交叉策略采用基因子段的整体交叉，变异时采用位置交换、逆序、插入等策略。最后，利用标准测试库中的实例进行仿真，并与已知最优值进行对比分析，结果表明，算法具有一定的可行性和有效性。

聚类车辆路径；差分进化算法；遗传算法；混合交叉算子；装载率

1 引言

车辆路径问题（VRP）属于一类经典的组合优化问题，也是NP难问题，自1959年被Dantzig和Ramser[1]首次提出以来，一直受到国内外研究者的广泛关注。聚类车辆路径问题（the Clustered Vehicle Routing Problem，CluVRP）作为有能力约束车辆路径问题（CVRP）的一个变种，由Sevaux M和Sörensen K[2]于2008年首次提出，主要基于如下假设：所有的客户根据其地理位置被预先分成若干个聚类；当某辆车访问某个聚类时，必须连续不断地访问该聚类里的所有客户，只有当其中的每一个客户均被访问完毕，车辆才能返回车场或者访问下一个聚类。CluVRP也可以看作是广义车辆路径问题[3-4]（the Generalized Vehicle Routing Problem，GVRP）的扩展情况，其区别为：GVRP问题中，车辆只访问每个聚类中的一个客户，而CluVRP问题中，车辆需要访问聚类中的每个客户。当前，聚类车辆路径问题在实际生活中的应用并不鲜见，如在快递行业，快递公司根据事先划分的片区，安排若干辆快递车负责多个社区（每个社区可对应一个问题中的聚类，其内部包括多个客户），当某车辆前往某社区取送件时，必须将社区内的所有客户全部服务完，才能离开该社区返回分拨中心或前往下一个社区。针对此类问题，需要解决的是在车辆装载能力、车辆数量等约束条件下，合理地为每辆车分配聚类，确定聚类的访问顺序，以及每个聚类内的客户服务顺序，显然，此类问题属于一个典型的两级优化问题。

目前有关聚类车辆路径问题的文献中，Christof Defryn等[5-6]建立了相应的整数规划模型，运用两级变邻域搜索算法进行求解；在聚类层，将问题转化为一维的装箱问题，利用最佳匹配递减算法构造聚类层的初始解，并设计一种聚类间的交换操作，以修复聚类层的不可行解；在聚类层的邻域结构上，设计了相应的交换、插入、2-Opt、Or-Opt算子；在客户层，利用一种转换算子生成每个聚类内的客户顺序，即客户层的初始解，并设计了客户的交换、插入、2-Opt、Or-Opt等操作。Battarra M等[7]采用分支切割算法和分支切割定价算法进行了求解。Barthélemy等[8]通过引入一个距离修改算子，在分属不同聚类的客户间加入一个较大的惩罚距离M，确保车辆必须连续服务完每一个聚类内的所有客户，从而将CluVRP问题转化为CVRP问题，最后用模拟退火算法进行了求解。Vidal T等[9]分别提出了基于迭代的邻域搜索算法和混合遗传算法来进行求解。Pop P和Chira C[10]等通过将问题中的每个聚类用一个虚拟的超级节点代替，将原问题转化为一个全局图，并利用遗传算法进行了求解。Andrei Horvat Marc和Petric a C Pop等[11]也利用了超级节点这一思路，令超级节点位于该聚类的重心，用遗传算法求解超级节点之间的最佳路线，并运用模拟退火算法求解每个聚类内的最短哈密顿路径。Izquierdo E C等[12-13]将问题分解成两层，每个聚类用一个虚拟中心代替，运用记录更新法（Recordto-Record algorithm）优化虚拟中心间的路径，而每个虚拟中心内部构成一条哈密顿路径，运用三类启发式算法进行求解。

截至目前，国内对聚类车辆路径问题的研究几乎处于空白，仅有部分文献将聚类算法运用于各种车辆路径问题中，如陈美军等[14]针对多车场车辆路径问题，提出了一种新的聚类蚁群算法；刘长石等[15]针对多辆车协作的随机车辆路径问题，设计了相应的模糊聚类和车辆协作策略；刘旺盛等[16]针对需求可拆分的车辆路径问题,分析了客户需求不可拆分的条件，提出了一种符合解的特征的聚类算法；向婷[17]等也针对需求可拆分车辆路径问题,提出了一种先分组、后路径的聚类算法。

综上所述，目前有关聚类车辆路径问题的研究主要是集中于精确算法（如分支定界算法、分支切割定价算法）、启发式算法（如邻域搜索算法）和部分智能优化算法（如遗传算法、模拟退火算法），差分进化算法作为一种具有较强全局搜索能力的智能优化算法，在该问题中的应用尚未出现。本文针对此类问题，首先构建问题的模型，然后运用基于差分进化和遗传算法的混合算法进行优化，在聚类层运用差分进化算法寻优，染色体直接采用基于聚类编号的编码，而客户层运用遗传算法求解，染色体直接采用基于客户编号的编码。

2 问题描述

聚类车辆路径问题可以描述为：在一个完全无向图G=(V,E)中，V={ }0,1,2,...,n表示由车场0和客户1,2,...,n构成的集合，E={(i,j)|i,j∈V,i≠j} 表示V中任意两个顶点所构成的边的集合；集合V={0 ,1,2,...,n}被预先按地理位置分成N+1个聚类V0,V1,V2,...,VN，其中聚类V0仅包含车场0，其他聚类V1,V2,...,VN均不含车场，无交集且至少包含一个客户顶点，根据该问题的特征，有V=V0⋃V1⋃V2...⋃VN，对于任意l,p∈{0 ,1,2,...,N} 且l≠p，有Vl⋂Vp=ϕ；对于任意两个顶点i≠j，其距离为dij；每个客户i∈{ }

1,2,...,n只能被一辆车提供服务，其货物需求量为qi；车场共有m辆车，其额定载重量为Q，对于每个客户i∈{ }

1,2,...,n，均有qi≤Q，且每辆车只能有一条运输路线。

本节描述的聚类车辆路径问题属于一类典型的两级优化问题，其中第一级为聚类层，即先将各个聚类分配给车辆，并确定同一个路线中车辆访问聚类的顺序；第二级称为客户层，在聚类的分配和顺序已安排的前提下，进一步安排每个聚类中车辆访问客户的顺序。该问题的优化目标为：在满足如下三条约束的前提下，将聚类在车辆之间合理地分配，并寻求车辆访问聚类的最优顺序和聚类内的客户最优顺序，使得所有车辆的总行驶距离最短。

（1）每辆车均从车场出发，为客户提供服务后，需返回车场；（2）当车辆进入某个聚类后，必须连续不断地为该聚类内的所有客户提供服务，直至完毕，才能进入下一个聚类或返回车场；（3）车辆所在路线中客户需求量之和不得超过车辆额定载重量Q。

如图1为一个车场、15个客户构成的完全无向图，其中15个客户被分成5个聚类。存在两条运输路线，车辆访问聚类的顺序分别为：V0-V1-V2-V3-V0，V0-V5-V4-V0，称为聚类层子路径；车辆访问客户的顺序分别为：0-1-2-3-4-5-6-0，0-15-14-13-12-11-10-9-8-7-0，称为客户层子路径。

3 问题模型

定义问题的变量为yik、xijk，其含义分别为：

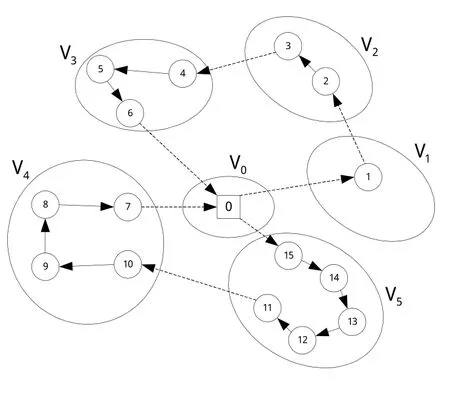
图1 聚类车辆路径问题示意图

该问题的模型如下：

该模型中：式（1）表示该模型的目标函数为极小化所有车辆的总行驶距离；式（2）表示每个客户由且仅由一辆车提供服务；式（3）、（4）表示yik和xijk之间的关系，且每个客户只能被服务一次；式（5）表示车辆的载重能力约束；式（6）表示消去子回路约束，其中|R|表示集合R中的客户个数；式（7）表示每个聚类仅被一辆车服务；式（8）表示车辆从车场出发，服务完客户后需要返回车场；式（9）表示聚类Vp中的客户需连续被服务，|Vp|为聚类Vp中的客户个数。

4 算法介绍

4.1 运用差分进化算法优化聚类层

差分进化算法是Rainer Storn在1996年IEEE会议上首次提出的一种智能优化算法[18]，该算法的结构与遗传算法类似，通过变异、交叉、选择等操作算子进行寻优，具有鲁棒性强、易执行、易理解等特点。

4.1.1 扫描算法初始化种群。聚类层染色体采用聚类编号1,2,...,N的一个重排表示，车场所在聚类0不计入其中，如图1中聚类层的编码结构可以表示为[1,2,3,5,4]。为提高聚类层初始种群的质量，借鉴文献[19]中的扫描算法进行初始化，具体方法如下：

首先对每个聚类，依次比较其中各客户与车场的连线和车场所在横坐标轴正向之间的夹角（0-360o），令最小的夹角为该聚类的X轴正向角度值；然后对各个聚类按X轴正向角度值升序排列；最后随机选择一个聚类作为起始点，按照逆时针方向，依次将后面的聚类安排在染色体中；重复前面步骤可得到种群规模为popsize_clu的聚类层染色体种群pop_clu。每条聚类层染色体均可按照下述步骤Step1-Step4生成可行的聚类层子路径：

Step1:选择第1辆车执行任务。

Step2:选择排列中最左边的聚类，计算该聚类中所有客户的总需求量，按公式（5）判断该聚类加入车辆所在路线后是否超载，若不超载，则将聚类安排给当前车辆；否则，新开一辆车，将聚类安排给新开的车。

Step3:将该聚类从排列中删除。

Step4:重复Step2和Step3，若所有的聚类均安排完毕，则获得可行的聚类层子路径，即将聚类在车辆间分配完毕，并获得车辆访问聚类的顺序。

4.1.2 基于升序排列的变异操作。差分进化算法与遗传算法的主要区别在于，其变异后的中间染色体v通过三个随机的父代染色体pop_clu(a,:)、pop_clu(b,:)、pop_clu(c,:)的基因值差分计算产生，即v=pop_clu(c,:)+F[pop_clu(a,:)-pop_clu(b,:)]，其中F为缩放因子，为区间[0,1]内的常数。由于变异后的中间染色体v的基因值会包含实数甚至负数，不再符合前述编码为{1,2,...,N}的重排的特点，因此需要对中间染色体v的基因按照基于升序的排序规则重新调整：设生成的中间染色体v的基因值为(min,max)内的实数，min是其最小基因值，max是其最大基因值，先对其每个位置的基因值按照升序进行排列，然后将基因值min对应的位置用“1”代替，第2小基因值对应的位置用“2”代替,依次类推，基因值max对应位置用“N”代替。

例如，经过变异后得到的中间染色体v为[-0.8,3.4,2.5,6.7,-5.4,9.7,4.8]，则利用前述规则进行调整后，该中间染色体v调整为[2,4,3,6,1,7,5]。

4.1.3 混合交叉操作。传统差分进化算法的交叉操作是基于当前染色体pop_clu(i,:)和变异后得到的中间染色体v的交叉，通常是随机选择一个位置，其基因来自于v，其余位置由交叉概率因子决定其基因来自pop_clu(i,:)或v，经验证，传统的交叉机制不再适用于具有上述编码结构的聚类层染色体，因为会导致交叉后的染色体中两个位置的基因完全一样，破坏原来的编码规则，因此，本文采用如下混合交叉策略：先对父代染色体pop_clu(i,:)和中间染色体v分别进行解码，得到各条聚类层子路径，然后计算各聚类层子路径的H值，将H值最大的子路径交换至对方染色体首部，并消去后面相同的元素，得到两个新的染色体pop_clu(i,:)new和vnew。H值的定义如下：

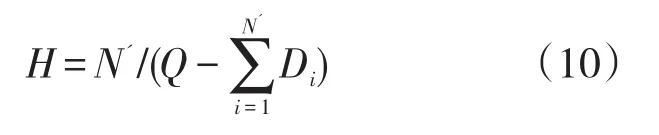
式（10）中N'为该聚类层子路径中包含的聚类个数。N'越大，表示车辆服务的聚类越多，则H值越大，在交叉时该段基因应优先被保留；Di为第i个聚类的需求量，车辆服务的所有聚类总需求量越大，则车辆的剩余载重能力越小，车辆利用率越高，在交叉时同样该段基因应优先被保留。

如图2表示父代染色体pop_clu(i,:)为[3,2,5,4,7,1,8,6]，经过解码后其H值最大的子路径对应的基因段为4-7-1-8，图2中上部分虚线框所示；中间染色体v为[5,6,1,8,3,2,7,4]，经过解码后其H值最大的子路径对应的基因段为1-8-3-2。经过交叉后消去后面相同的元素，如图2中阴影部分所示，得到新的染色体pop_clu(i,:)new和vnew。

图2 聚类层染色体交叉算子示意图

4.1.4 选择操作。差分进化算法的选择操作采用贪婪策略，将交叉操作得到的染色体pop_clu(i,:)new和vnew与父代染色体pop_clu(i,:)进行比较，选择最优的聚类层染色体作为子代，具体而言：针对每条聚类层染色体，先调用客户层的遗传算法，寻找所对应的最优客户层染色体和目标值，其目的是在聚类层子路径确定后，搜寻能使得总行驶距离最短的客户层子路径，并将最短的总行驶距离返回给对应的聚类层染色体，作为其差分进化算法选择操作时计算适应度的依据。

4.2 运用遗传算法优化客户层

4.2.1 扫描算法初始化种群。客户层染色体采用基于客户编号的方式。由于车辆进入聚类后，需连续不断地访问聚类中的所有客户，因此客户层染色体以聚类层染色体为依据，按车辆访问聚类的先后顺序，将每个聚类所属的客户组成一个基因子段依次排列。如4.1节中当聚类层染色体表示为[1,2,3,5,4]时，其对应的客户层染色体包含5个基因子段，根据图1所示，编码[1‖2 3‖4 5 6‖15 14 13 12 11‖10 9 8 7]和[1‖3 2‖4 6 5‖14 15 13 11 12‖7 8 9 10]均为该聚类层染色体对应的客户层染色体。借鉴4.1节中的思路，同样可利用扫描算法生成种群规模为popsize_custom的客户层染色体种群pop_custom，只是需在每个聚类的空间范围内进行扫描生成相应的基因子段。

4.2.2 选择操作。采用赌轮选择。

4.2.3 基于基因子段的整体交叉。由于同一个聚类中的客户必须被连续访问，因此，在以一定的交叉概率pos_cross进行客户层染色体之间的交叉操作时，必须将某一个聚类中的客户整体交叉，如图3所示为同时将两个客户层染色体中的第2个基因子段和第5个基因子段交换。

图3 客户层染色体交叉算子示意图

4.2.4 变异操作。在以一定的变异概率pos_mutation对客户层染色体进行变异时，采用位置交换、逆序、插入等操作，具体操作时随机选择一种上述操作方式，必须保证原客户所属的基因子段不变。如图4分别为对客户层染色体第4个基因子段进行三种变异操作：将客户15和客户11进行位置交换、将客户11插入到客户15前面、将客户15至客户11之间的5个基因整体逆序。

5 算法步骤

本文算法的总体步骤如下：

Step1：参数初始化。设置聚类层染色体种群规模popsize_clu、差分进化算法最大迭代次数max_iter_clu、缩放因子F、客户层染色体种群规模popsize_custom、遗传算法最大迭代次数max_iter_custom、遗传算法交叉概率pos_cross和变异概率pos_mutation等。

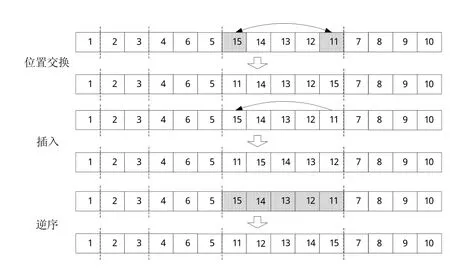
图4 客户层染色体三种变异操作算子示意图

Step2：利用扫描算法生成聚类层染色体种群pop_clu。对每个聚类染色体，调用函数GA_custom()搜寻其对应的最优客户层染色体best_custom和目标值Z。更新最优聚类层染色体best_clu及其对应的最优客户层染色体best_custom∗和最优目标值Z∗。

Step3：令iter←1。

Step4：令i←1，对聚类染色体pop_clu(i,:)执行差分进化算法变异操作，并利用基于升序的排序规则调整中间染色体v。

Step5：对染色体pop_clu(i,:)和染色体v进行交叉操作，得到两个新的染色体pop_clu(i,:)new和vnew。

Step6：对染色体pop_clu(i,:)new和vnew，分别调用函数GA_custom()，搜寻其对应的最优客户层染色体best_custom和目标值Z，并和pop_clu(i,:)的目标值进行比较，执行差分进化算法选择操作，选择三者中最优个体进入下一代，并更新最优聚类染色体best_clu、最优客户层染色体best_custom∗和最优目标值Z∗。令i=i+1，返回Step4，直至i＞popsize_clu。

Step7：令iter=iter+1 ，返 回 Step4，直 至iter＞max_iter_clu。

Step8：输出最优聚类染色体best_clu、最优客户层染色体best_custom∗和最优目标值Z∗。

其中，函数GA_custom()的步骤如下：

Step1.1：根据聚类染色体中的车辆聚类分配和聚类访问顺序，结合扫描算法生成对应的客户层染色体种群pop_custom。

Step1.2：计算每个客户层染色体对应的目标值Zcustom，更新最优客户层染色体best_custom和其目标值

Step1.3：令t←1

Step1.4：执行客户层染色体选择操作。

Step1.5：按照交叉概率pos_cross执行交叉操作。

Step1.6：按照变异概率pos_mutation执行变异操作，并计算变异后染色体的目标值Zcustom，更新best_custom和其目标值

Step1.7：令t=t+1 ，返 回 Step1.4，直 至t＞max_iter_custom。

Step1.8：返回best_custom和，将赋给Z。

6 仿真实验分析

以文献[5]中所介绍的A、B、P、G、M类标准测试库为例进行仿真实验，该测试库仿真实例以X-n-kc-v的结构表示，不同于本文前面正文中部分符号所代表的含义，此处X代表测试库类型（如A、B、P、G、M类）、n代表顶点数（包括客户和车场）、k代表相应CVRP问题中的车辆数、c代表聚类数、v代表CluVRP问题中的车辆数。相关参数设置见表1。

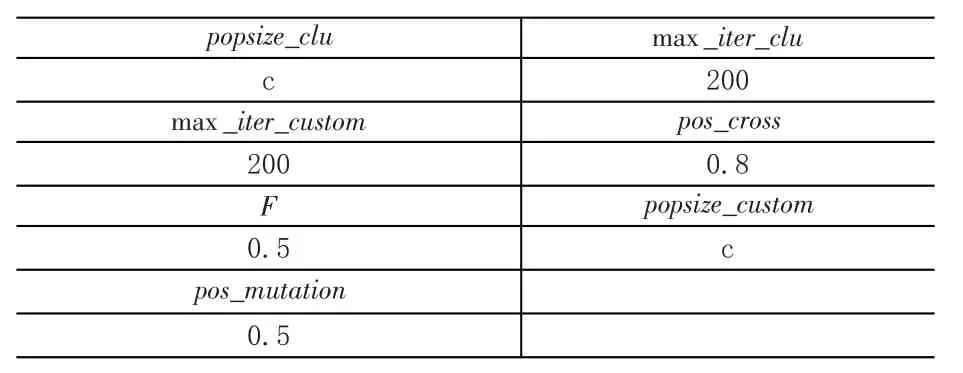
表1 算法参数设置

6.1 仿真结果

利用Matlab R2016进行编程，运行环境为Intel i5-5200U、CPU2.2GHZ，4G内存。以A-n33-k5-C11-V2为例，经过仿真，得到最优目标值为472，共包含2条子路径，如图5所示，聚类层和客户层的子路径分别为：

聚类层子路径1：0-9-1-5-3-10-8-0，对应的客户层子路径为：0-21-33-14-9-8-27-5-13-6-28-26-31-11-18-10-4-17-16-23-0；聚类层子路径2：0-4-6-2-7-11-0，对应的客户层子路径为：0-3-25-7-20-15-22-2-30-32-19-29-12-24-0。

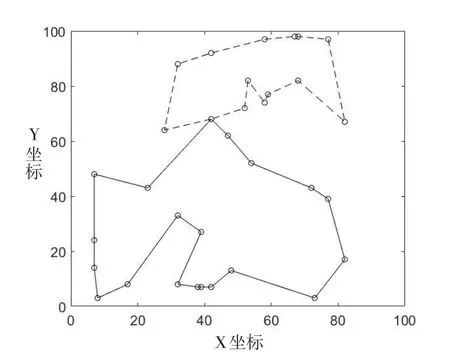
图5 实例A-n33-k5-C11-V2的路径

其迭代示意图如图6所示。

图6 实例A-n33-k5-C11-V2迭代示意图

另以M-n200-K16-c67-v6为例，通过仿真，得到如图7所示的六条子路径，其对应的总行驶距离为929。

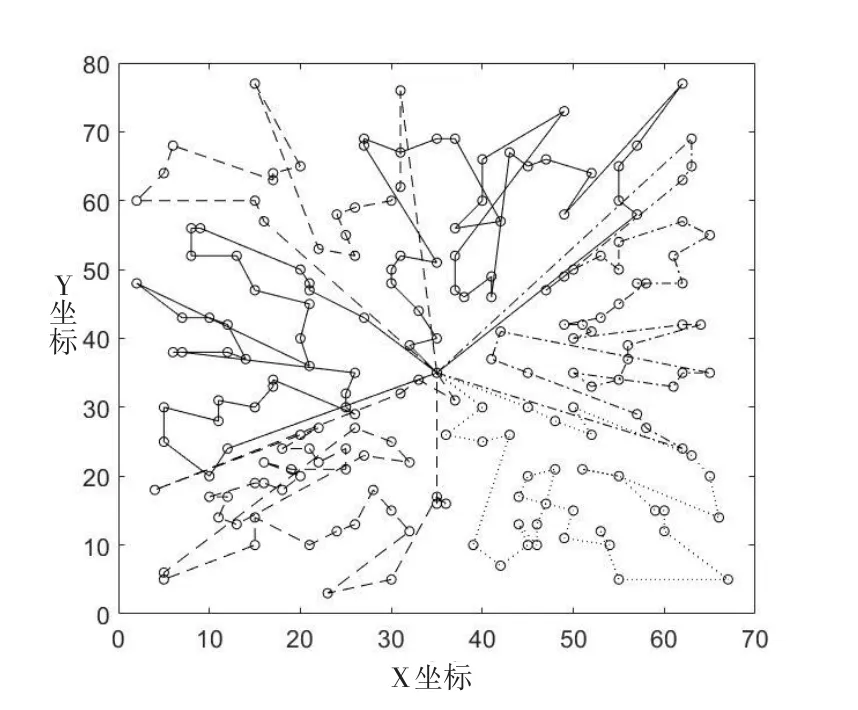
图7 实例M-n200-K16-c67-v6路径

6.2 实验结果对比分析

运用本文所提算法，选取A、B、P、G、M类型测试库共20个实例进行仿真，每个测试实例随机运行10次，将10次运行结果的最优值、平均值与已知最优值[5]进行比较，见表2。

表2 本文算法结果与已知最优值对比分析

通过比较可知，本文所提算法在解决客户数100以内的中小规模问题时，基本能搜索到问题的最优解，这得益于算法在初始化聚类层染色体种群时，采用扫描算法，在一定程度上提高了初始种群的质量；在进行聚类层染色体交叉操作时，充分考虑了服务聚类数和装载率等因素，优先保留H值大的基因子段，同时，即使两个完全相同的染色体进行交叉，也能产生新的子代染色体，这使得算法能一定程度上跳出局部最优；在客户层染色体遗传算法中，通过基因子段的整体操作，扩大了遗传算法的搜索空间，同时运用逆序、插入、交换等变异算子，尽可能地保证了一定的局部搜索能力。

当然，本文所提算法还存在一定不足，在解决大规模CluVRP问题时，得到的解还不甚满意，与已知最优值尚有一定偏差，随着问题规模的增加，算法寻优时间不断增加，如何进一步优化算法的性能，以加强针对大规模CluVRP问题的寻优能力，是今后进一步研究的方向。

7 结论

本文针对客户被预先划分给聚类的聚类车辆路径问题，构建了相应的数学模型，通过基于差分进化算法和遗传算法的两级混合算法来进行优化，在算法的设计方面，聚类层染色体和客户层染色体的编码结构简单，运用扫描算法初始化两层染色体种群，通过在聚类层采用基于升序排列的变异操作和考虑聚类服务数、车辆载重率的混合交叉算子，以及在客户层采用基于基因子段的整体交叉和多种变异算子等多种策略，较好地对该类问题进行了求解。

[1]Dantzig G B,Ramser J H.The Truck Dispatching Problem[M].INFORMS,1959.

[2]Sevaux M,Sörensen K.Hamiltonian paths in large clustered routing problems[A].Proceedings of the EU/MEeting 2008 workshop on Metaheuristics for Logistics and Vehicle Routing[C].2008.

[3]李大卫,王梦光.广义车辆路径问题—模型及算法[A].1997中国控制与决策学术年会论文集[C].1997

[4]Ghiani G,Improta G.An efficient transformation of the generalized vehicle routing problem[J].European Journal of Operational Research,2000,122(1):11-17.

[5]Defryn C,Sörensen K.A fast two-level variable neighborhood search for the clustered vehicle routing problem[J].Computers&Operations Research,2017,83:78-94.

[6]Defryn C,Sörensen K.A two-level variable neighbourhood search for the euclidean clustered vehicle routing problem[R].2015.

[7]Battarra M,Erdogan G,Vigo D.Exact Algorithms for the Clustered Vehicle Routing Problem[J].Operations Research,2014,62(1):58-71.

[8]Barthélémy T,Rossi A,Sevaux M,et al.Metaheuristic approach for the clustered VRP[A].EU/ME 2010[C].2010.

[9]Vidal T,Battarra M,Subramanian A,et al.Hybrid metaheuristics for the Clustered Vehicle Routing Problem[J].Computers&Operations Research,2015,58:87-99.

[10]Pop P,Chira C.A hybrid approach based on genetic algorithms for solving the Clustered Vehicle Routing Problem[A].Evolutionary Computation[C].2014.

[11]Marc A H,Fuksz L,Pop P C,et al.A Novel Hybrid Algorithm for Solving the Clustered Vehicle Routing Problem[M].Springer International Publishing,2015.

[12]Izquierdo E C,Rossi A,Sevaux M.Modeling and Solving the Clustered Capacitated Vehicle Routing Problem[A].Proceeding of the 14thEU/ME workshop[C].2013.

[13]Expósito-Izquierdo C,Rossi A,Sevaux M.A Two-Level solution approach to solve the Clustered Capacitated Vehicle Routing Problem[J].Computers& IndustrialEngineering,2016,91:274-289.

[14]陈美军,张志胜,陈春咏,等.多车场车辆路径问题的新型聚类蚁群算法[J].中国制造业信息化,2008,37(6):1-5.

[15]刘长石,赖明勇.基于模糊聚类与车辆协作策略的随机车辆路径问题[J].管理工程学报,2010,24(2):75-78.

[16]刘旺盛,杨帆,李茂青,等.需求可拆分车辆路径问题的聚类求解算法[J].控制与决策,2012,27(4):535-541.

[17]向婷,潘大志.求解需求可拆分车辆路径问题的聚类算法[J].计算机应用,2016,36(11):3 141-3 145.

[18]Storn R.Differential evolution design of an IIR-filter[A].IEEE International Conference on Evolutionary Computation[C].1996.

[19]吴天羿,许继恒.基于混合遗传算法的模糊需求车辆路径问题[J].解放军理工大学学报(自然科学版),2014,(5):475-481.

Study on Clustered VRP Based on Hybrid Differential Genetic Algorithm

Zhu Hao
(Huzhou Vocational&Technical College,Huzhou 313000,China)

In this paper,in view of the routing problem of all the customer vehicles assigned to certain clusters in advance,we built the corresponding integer programming model,and proposed the bi-level hybrid algorithm based on the differential evolution and GA,according to which,at the cluster level,the differential evolution algorithm was used for optimization purpose,the mutation operator was designed based on ascending sort and considering the inadequacy of the traditional differential evolutionary algorithm in the crossover link,the hybrid crossover operator was designed to account for the quantity of clustering service and loading rate;at the customer level,the GA was used for optimization purpose,the chromosomes encoded based on customer numbering and different strategies adopted during the mutation.At the end,we had a simulation study regarding an empirical case from the standard test library and compared the result with the established optimal value to show the feasibility and validity of the algorithm of this paper.

clustered vehicle routing;differential evolutionary algorithm;genetic algorithm;hybrid crossover operator;loading rate

F224.0;F252.14

A

1005-152X(2017)10-0075-08

10.3969/j.issn.1005-152X.2017.10.016

2017-09-10

湖州市自然科学基金（2015YZ07）；浙江省高等教育课堂教学改革项目（kg2015786）

朱颢，讲师，硕士，主要研究方向：车辆路径问题、物流工程。