涡轮叶片疲劳-蠕变寿命稳健性优化方法
2017-11-13陈志英
陈志英,王 朝,周 平
(北京航空航天大学能源与动力工程学院,北京100191)
涡轮叶片疲劳-蠕变寿命稳健性优化方法
陈志英,王 朝,周 平
(北京航空航天大学能源与动力工程学院,北京100191)
为了清晰地反映涡轮叶片的疲劳-蠕变交互作用,提高寿命预测结果的准确性及可靠性,并改善涡轮叶片疲劳寿命对随机变量的敏感程度,分别采用Manson-Coffin公式和Larson-Miller方程计算了涡轮叶片的低循环疲劳寿命和蠕变持久寿命,利用修正的时间-寿命分数法计算了涡轮叶片疲劳-蠕变损伤,在此基础上,将响应面法(RSM)与果蝇优化算法(FFOA)相结合,考虑载荷、材料参数、疲劳-蠕变交互程度的不确定性,对涡轮叶片疲劳寿命进行了稳健性优化设计。优化结果表明:涡轮叶片疲劳-蠕变小时寿命的概率区间减小了8.48%,验证了该优化方法的工程可行性。
涡轮叶片;疲劳-蠕变;寿命预测;稳健性优化设计;时间-寿命分数法;航空发动机
0 引言
涡轮转子结构的疲劳-蠕变失效是导致发动机非计划换发的重要因素之一,从发动机的使用可靠性和经济性的角度来讲,对涡轮部件进行寿命评估是十分必要的。随着航空发动机性能的提高、诸多新型材料的出现,带来的是更多的不确定因素,传统的疲劳寿命确定性分析方法已经无法满足设计需要,因此,以概率分析为基础的稳健性优化设计方法便应运而生[1-2]。
有关疲劳理论、寿命预测、结构不确定性分析的研究工作,主要集中在以下几个方面:材料本构关系、多轴疲劳、连续损伤力学、断裂力学等方面的研究理论相继提出,为疲劳寿命预测提供了广泛的基础和方向[3-5];考虑到疲劳寿命的分散性,引入可靠度的概念,将低循环疲劳寿命预测模型与人工智能算法相结合,对涡轮部件进行概率可靠性分析与优化设计[6-7];随着试验条件的进步以及数值计算软件的普及,将有限元法与试验结合的方式近些年获得了持续关注和认可,从而更加方便地对疲劳寿命预测模型、材料本构关系理论等进行评估分析[8-9]。
在实际工况下,涡轮叶片在不同位置处应力集中程度和温度场存在差异,其失效形式也具有多样性,涡轮叶片的低循环疲劳损伤与蠕变损伤存在交互作用,总损伤并不是二者简单的线性叠加[10]。在服役过程中,载荷、材料、工艺、几何尺寸等参数都具有一定的随机性,并满足某种分布规律,而确定性计算中的参数值通常只是这些参数的平均值,因此有必要对影响发动机可靠性的因素进行合理的控制和优化。
本文以涡轮叶片为研究对象,基于有限元法,从涡轮叶片疲劳-蠕变寿命的确定性分析出发,考虑随机变量的分散性,构建了涡轮叶片疲劳-蠕变寿命近似函数模型,并进行概率分析和稳健性优化。
1 涡轮叶片热-结构耦合分析
涡轮叶片几何模型如图1所示,在建模过程中不考虑叶片内部及榫齿处的冷却通气孔,忽略叶片根部存在的倒圆等,这样做会使计算出的应力结果偏大,但最终获得的循环寿命值却是有安全裕度的。在进行网格划分时,在尺寸变化处进行网格细化。约束榫槽法向自由度、榫齿前后端面的轴向自由度,避免产生刚体位移。涡轮叶片材料为定向凝固高温合金DZ22,具体的材料性能参数可以查询手册[11]。首先进行稳态热分析,所得温度场作为结构分析的边界条件。因涡轮叶片受到的振动应力和气动力对低循环疲劳-蠕变寿命的影响甚微,因此仅考虑离心力和热负荷。其中,离心力按载荷谱中典型功率状态计算,热负荷为相应功率状态的稳态温度场,以90%转速状态为例,温度场计算结果如图2所示,对应的应力、应变分布如图3、4所示。
计算结果表明:榫齿、叶根、缘板与伸根交界处均出现了较为严重的应力集中,最大应力位于叶背榫齿排气边,综合考虑叶片的受力情况和温度分布,选取榫齿处最大应力点作为寿命预测关键点。从数值上看,最大等效应力为967.7 MPa,对应最大应变为8.336×10-3,出现在第1榫齿叶背排气边,该点对应温度为635℃,同理可以计算出各个典型转速状态下,寿命预测关键点的应力和应变,结果见表1。

表1 各转速状态下的应力应变结果
2 疲劳-蠕变寿命确定性分析
2.1 寿命计算模型
当材料处于弹性范围时,平均应力对疲劳寿命的影响较大,低循环疲劳寿命计算选取带Morrow平均应力修正的Manson-Coffin公式
蠕变持久寿命的预测广泛应用Larson-Miller方程,在工程上常运用热强综合参数方程来进行具体计算。蠕变持久寿命通常是应力和温度的函数
式中:a0,a1,a2,a3 均为常数,tb 为蠕变断裂时间。
2.2 损伤累积模型
当考虑疲劳-蠕变的交互作用时,常使用时间-寿命分数法进行寿命预测,以Miner线性累积损伤理论为基础
式中:m是某块载荷谱内具有的应力循环数;i(i=1,2,…,m)是某应力循环出现的频次;第i个应力循环对应的等幅疲劳寿命为Ni;ti为第i次起落循环的保载时间;tbi为对应的蠕变断裂时间;Df和Dc分别代表疲劳累积损伤和蠕变累积损伤。
为反映疲劳-蠕变的交互作用程度,谢锡善[12-13]提出了另1种表达形式,该方法被证明有着较好的准确度,特别是以蠕变为主导形式的疲劳损伤
式中:B值大小反映交互作用的强弱,主要与温度有关,若 B>0,为正交互作用;若 B<0,为负交互作用;若B=0,表明无交互作用,符合线性累计损伤理论;n和1-n分别是疲劳损伤指数和蠕变损伤指数,体现了2种损伤所占比例。
经分析决定,保载时间t取12 h,因飞机巡航状态持续时间最长,蠕变持久寿命按83%转速状态进行计算,虽然这样的考虑较为极端,但得出的结果却是安全保守的;B取值为-1.20,因蠕变的作用使榫齿处的应力分布趋于均匀、应力水平下降,其寿命相对于纯低循环疲劳载荷作用下反而会有所延长。
2.3 载荷谱提取和疲劳-蠕变寿命预测
某真实航班的实测载荷数据经雨流计数 [14]的统计结果见表2,其飞行总时间约为12 h,共6个起落,典型转速循环有6种,除0-max-0主循坏外,还包含地面慢车-max-地面慢车,空中慢车-max-空中慢车等典型次循环。事实上,在巡航状态时,发动机转速并不是恒定不变的,依然存在小范围波动,属于高周循环,因单独考虑低循环疲劳时,其影响很小,可以忽略不计。
叶片危险点处的疲劳-蠕变交互损伤以及小时寿命计算结果见表2。由此可见,榫齿处的工作条件恶劣,最低小时寿命仅有15095 h,该位置决定了涡轮叶片的使用寿命,另外,从损伤比例来看,蠕变损伤同样不可忽视,在低循环疲劳寿命的预测过程中,经计算可知,次循环的损伤占循环总损伤的10.5%,与主循环相比,次循环损伤虽然很小,但不可忽略;对于小时寿命的计算,依次采用线性累计损伤法和考虑疲劳-蠕变交互作用的时间-寿命分数法,其计算结果分别为13528、15095 h,由此可见,与损伤线性叠加的方式相比,修正的时间-寿命分数法能够恰当地体现出疲劳-蠕变交互作用。
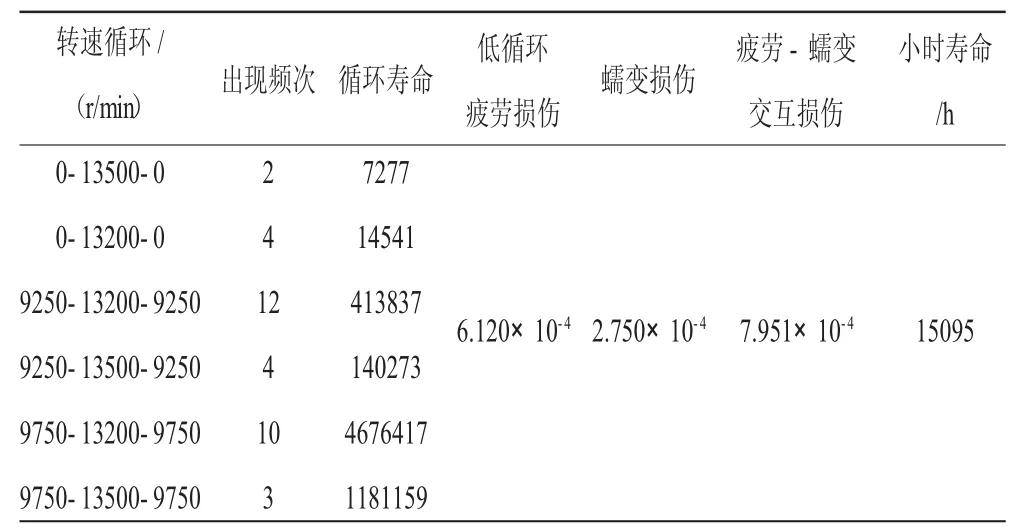
表2 典型转速循环下的涡轮叶片疲劳-蠕变寿命预测结果
3 疲劳-蠕变寿命概率分析及稳健性优化设计
3.1 基于响应面法的涡轮叶片疲劳-蠕变寿命概率分析
直接调用有限元程序进行抽样计算会耗费大量时间,工程上常采用响应面法(Response Surface Methodology,RSM)来代替繁琐的有限元计算,其基本思想是利用有限的样本点拟合出1个简单响应函数来等效真实的输出函数。含交叉项的二次多项式函数的拟合精度高,各随机变量能够被充分覆盖,适用于非线性程度较强的情况,因此用其拟合涡轮叶片疲劳-蠕变寿命与随机变量的关系更加合理。
式中:a0、ai、aij均为响应面方程待定系数,Xi代表载荷、材料参数等随机变量,N代表涡轮叶片疲劳-蠕变寿命。
基于有限元法,通过数值模拟将主要随机变量引入到寿命预测中,考虑载荷、材料等参数的随机性,建立响应面模型对涡轮叶片疲劳寿命进行概率分析,计算过程中仅考虑0-Max-0的主循环,为反映次循环对低循环疲劳总损伤的贡献,结合3.2的确定性分析结果,对低循环疲劳寿命予以适当的修正。
随机变量的选取及相应的分布规律见表3,假定各随机变量相互独立且均服从正态分布。其中转速ω、温度T代表了工况载荷的不确定性,疲劳强度系数、弹性模量E、疲劳强度指数b、疲劳塑性指数c,表明了材料参数存在不确定性,交互系数B体现了疲劳-蠕变交互程度的不确定性;修正系数V反映了对疲劳寿命修正过程的不确定性。

表3 随机变量及其分布规律
根据所选取的随机变量,在有限元软件中进行250组抽样计算,其中200组数据用于拟合响应面方程,剩余50组用来检验拟合效果,其结果表明:拟合相对误差仅为1.90%,精度良好。理论计算结果与响应面方程计算结果的对比如图5所示。
利用拟合好的响应面方程代替有限元计算,进行10000组抽样,得到叶片危险点处疲劳-蠕变的小时寿命分布如图6所示,从图中可见,小时寿命近似服从正态分布,其中高小时寿命区间出现频数低,总体分散性较大。
3.2 基于果蝇优化算法的涡轮叶片疲劳-蠕变寿命稳健性优化设计
随机变量的波动导致涡轮叶片疲劳-蠕变寿命分布具有较大的概率分布区间,因此,需要合理地选取优化可控变量,对涡轮叶片进行稳健性优化设计,稳健性设计基于2点原则:(1)使目标值接近最优均值,(2)使目标值的波动范围越小越好。
果蝇优化算法(Fruit Fly Optimization Algorithm,FFOA)是台湾学者潘文超提出的1种全局人工智能优化算法,基本思想是根据果蝇的位置计算其附近的食物味道浓度,然后向食物味道浓度最大或最小的地方飞去,通过反复迭代食物味道浓度来求取目标函数的最值[15]。
优化模型选取加权均方差法
其中:mu、sigma分别为小时寿命和标准差设计目标值;η为综合考虑目标均值与标准差的权重系数;利用分位数限制寿命分布的概率区间长度,并作为优化约束条件。选择转子转速ω和温度T,作为稳健性优化设计中的可控随机变量,其余参数作为不可控随机变量。
目标函数的迭代过程如图7所示,优化后的小时寿命分布如图8所示,表4和图9为优化前后结果对比。

表4 优化前后结果对比
显然,优化后的平均小时寿命提高至17078 h,寿命标准差减小至4257 h,寿命概率区间减小了8.48%,改善了涡轮叶片的疲劳寿命对随机变量的敏感度。
4 结论
以涡轮叶片为研究对象,先后对其进行了疲劳-蠕变寿命预测和稳健性优化设计,结论如下:
(1)涡轮叶片寿命预测结果表明:低循环疲劳次循环的损伤约占总损伤的10%,这部分损伤不可忽略;依次采用线性累计损伤法和考虑疲劳-蠕变交互作用的时间-寿命分数法,小时寿命计算结果分别为13528、15095 h,后者与前者相比,恰当地体现出疲劳-蠕变交互作用。
(2)用响应面方程来代替有限元计算,可以满足精度要求;考虑到疲劳寿命的分散性,特别是疲劳-蠕变交互程度的不确定性,采用稳健性优化设计方法,疲劳寿命概率分布区间减小了8.48%,在涡轮叶片的平均服役寿命延长至17078 h的同时,寿命标准差减小至4257 h。
(3)该寿命评估方法可为发动机进厂维修时间的确定提供依据,稳健性优化设计方法对其他结构的概率可靠性设计有一定的借鉴意义,二者结合,对于涡轮叶片乃至整个发动机结构的研制工作,都具有一定的参考价值。
[1]李其汉,王延荣.航空发动机结构强度设计问题[M].上海:上海交大出版社,2014:30-33.LI Qihan,WANG Yanrong.The design problem of aero-engine structure strength [M].Shanghai:Shanghai Jiao Tong University Press,2014:30-33(in Chinese)
[2]王荣桥,胡殿印,申秀丽,等.航空发动机典型结构概率设计技术[J].航空制造技术,2014,451(7):26-30.WANG Rongqiao,HU Dianyin,SHEN Xiuli,et al.Probabilistic design technology on typical structure of aero-engine[J].Aeronautical Manufacturing Technology,2014,(7):26-30.(in Chinese)
[3]董杰,陈学东,范志超,等.基于微裂纹扩展的疲劳蠕变寿命预测方法[J].金属学报,2008,44(10):1167-1170.DONG Jie,CHEN Xuedong,FAN Zhichao,et al.A new fatigue-creep life prediction metrology.[J].Acta Metallurgica Sinica,2008,44(10):1167-1170.(in Chinese)
[4]孙瑞杰,闫晓军,聂景旭.定向凝固涡轮叶片高温低周疲劳的破坏特点[J].航空学报,2011,32(2):337-343.SUN Ruijie,YAN Xiaojun,NIE Jingxue.Failure characteristics of directional solidification turbine blade under high temperature low cycle fatigue load[J].Acta Aeronautica et Astronautica Sinica,2011,32(2):337-343.(in Chinese)
[5]彭立强,王健.涡轮叶片多轴低周疲劳/蠕变寿命研究 [J].燃气轮机技术,2009,22(2):26-29.PENG Liqiang,WANG Jian.Research of multiaxial fatigue-creep life prediction for turbine blade[J].Gas Turbine Technology,2009,22(2):26-29.(in Chinese)
[6]周平,白广忱.基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J].航空动力学报,2013,28(5):1013-1018.ZHOU Ping,BAI Guangchen.Robust design of turbine-blade low cycle fatigue based on neural networks and Fruit Fly Optimization Algorithm[J].Journal of Aerospace Power.2013.28(5):1013-1018.(in Chinese)
[7]白斌,白广忱,李超.基于FE-ERSM航空发动机叶盘结构可靠性研究[J].振动、测试与诊断,2014,34(5):823-831.BAI Bin,BAI Guangchen,LI Chao.Reliable research of the blade disk assemblies of aero-engine based on FE-ERSM[J].Journal of Vibration,Measurement&Diagnosis,2014,34(5):823-831.(in Chinese)
[8]胡殿印,王荣桥,侯贵仓,等.涡轮构件疲劳/蠕变寿命的试验方法[J].推进技术,2010,31(3):331-334.HU Dianyin,WANG Rongqiao,HOU Guicang,et al.Experment on fatigue-creep life of turbine components[J].Journal of Propulsion Technology,2010,31(3):331-334.(in Chinese)
[9]张国乾,赵明,章胜,等.基于Walker等效应变的涡轮盘低周疲劳寿命预测[J].航空材料学报,2013,33(6):81-85.ZHANG Guoqian,ZHAO Ming,ZHANG Sheng,et al.Low cycle fatigue life prediction of turbine disks based on walker equivalent strain[J].Journal of Aeronautical Materials,2013,33(6):81-85.(in Chinese)
[10]闫晓军,聂景旭.涡轮叶片疲劳 [M].北京:科学出版社,2014:55-56.YAN Xiaojun,NIE Jingxu.Fatigue of turbine blade[M].Beijing:Science Press,2014:55-56.(in Chinese)
[11]《中国航空材料手册》编辑委员会.中国航空材料手册(第2版),第2卷[M].北京:中国标准出版社,2001.Editorial Committee of China Aeronautical Materials Handbook.China aeronautical materials handbook(2nd ed),Vol.2[M].Beijing:China Standard Press,2001.(in Chinese)
[12]Lagneborg R,Attermo R.The effect of combined low-cycle fatigue and creep on the life of austenitic stainless steels[J].Metallurgical Transactions,1971,2(7):1821-1827.
[13]陈立杰.某航空发动机低压涡轮叶片蠕变-疲劳交互作用寿命预测[D].东北大学,2005.CHEN Lijie.Life prediction method of aero-engine low pressure turbine blades under creep-fatigue interaction[J].Northeastern University,2005.(in Chinese)
[14]Matsuishi M,Endo T.Fatigue of metals subjected to varying stress[J].Japan Society of Mechanical Engineers,Fukuoka,Japan,1968,68(2):37-40.
[15]Pan W T.A new Fruit Fly Optimization Algorithm:taking the financial distress model as an example.[J].Knowledge-Based Systems,2012,26(2):69-74.
[16]李骏,宋友辉,刘汉斌,等.涡轮叶片-榫齿-轮盘的蠕变与低循环疲劳寿命预测[J].推进技术,2015(11):1699-1704.LI Jun,SONG Youhui,LIU Hanbin,et al.Creep and low cycle fatigue life prediction for turbine[J].Journal of Propulsion Technology,2015(11):1699-1704.(in Chinese)
[17]刘存,孙志刚,胡绪腾,等.某型发动机第2级涡轮叶片低循环疲劳寿命分析[J].航空发动机,2009,35(2):30-33.LIU Cun,SUN Zhigang,HU Xuteng,et al.Analysis of low cycle fatigue life for second-stage turbine blade of an aeroengine[J].Aeroengine.2009,35(2):30-33.(in Chinese)
Robust Optimization Method for Turbine Blade under Fatigue-Creep Interaction
CHEN Zhi-ying,WANG Chao,ZHOU Ping
(School of Energy and Power Engineering,Beihang University,Beijing 100191,China)
In order to reflect fatigue-creep interaction of turbine blade clearly,raise the accuracy and reliability of life prediction result and improve sensitivity of fatigue life to random variables at the same time.low cycle fatigue life and creep life of turbine blade were calculated by Manson-Coffin formula and Larson-Miller equation,fatigue-creep damage was obtained by modified time-life fraction method.Robust optimization design of turbine blade fatigue life was developed by combining RSM (Response Surface Methodology)and FFOA (Fruit Fly Optimization Algorithm),considering the uncertainty of loads,material parameters and the degree of fatigue-creep interaction.The results show that probability interval of fatigue-creep life for turbine is decreased by 8.48%,which verify the feasibility of this optimization method.
turbine blade;fatigue-creep;life prediction;robust optimization design;time-life fraction method;aeroengine
V231.95
A
10.13477/j.cnki.aeroengine.2017.04.003
2016-12-17
陈志英(1960),男,博士生导师,博士,主要研究方向为航空发动机结构优化设计、可靠性及维修性工程。E-mail:chenzhiying@buaa.edu.cn
陈志英,王朝,周平.涡轮叶片疲劳-蠕变寿命稳健性优化方法[J].航空发动机,2017,43(4):11-16.CHEN Zhiying,WANG Chao,ZHOU Ping.Robust optimizationmethod for turbine blade under fatigue-creep interaction[J].Aeroengine,2017,43(4):11-16.
