基于多铁纳磁体的择多逻辑门三维磁化动态特性研究∗

危波 蔡理 杨晓阔 李成

(空军工程大学理学院,西安 710051)

基于多铁纳磁体的择多逻辑门三维磁化动态特性研究∗

危波 蔡理†杨晓阔 李成

(空军工程大学理学院,西安 710051)

(2017年5月27日收到;2017年7月25日收到修改稿)

多铁纳磁体,择多逻辑门,应变时钟,磁化动态

1 引 言

随着互补金属氧化物半导体(CMOS)器件尺寸已经接近摩尔定律所描述的物理极限,传统CMOS技术面临着尺寸缩小带来的功耗、量子效应和散热等严重问题,因而越来越多的科研人员开始研究基于新技术的纳米器件[1−5].利用磁性材料沉积成一定形状的纳米薄膜可以制备纳磁逻辑器件(nanomagnet logic device,NMLD),NMLD具有天然非易失性、抗辐射和低功耗等优点,是“后CMOS时代”具有广泛影响的技术发现之一,这些特性使其在临近空间电子系统、存储器等方面具有广阔的应用前景[6,7].NMLD依靠磁体间的偶极子耦合作用进行逻辑传递,为了完成一次可靠的操作,通常需要施加一外部信号(电压或电流)将目标纳磁体预置到空态,以确保耦合作用能有效翻转目标纳磁体,这个外部信号就是NMLD的时钟[8,9].传统的时钟方案包括利用通电导线产生全局磁场[10,11],以及基于自旋转移扭矩形成时钟场[12,13]等.虽然纳磁体本身功耗极低,但全局磁场及自旋转移扭矩的产生均需要大电流,产生大电流的外部电路不可避免地存在大量的能量损失,因而它们并不是理想的时钟方案.最近,Atulasimha等[14]提出了一种基于多铁纳磁体的磁逻辑应变时钟,表现出了更加优越的性能(如工作频率为1 GHz时,自旋转移扭矩时钟能量损失为108kBT,而应变时钟功耗仅为200kBT).多铁纳磁体逻辑器件由压电层和磁致伸缩层构成,其结构如图1(a)所示,通过给压电层施加一微小电压,产生的应力通过压电层和磁层之间的磁弹耦合,能够使磁层的磁化翻转接近90°[8],该现象(尺寸为几十纳米的多铁纳磁体)已得到了实验验证[15,16].同时,应变时钟还可以对单个多铁纳磁体的磁化翻转进行控制,这也克服了传统时钟的磁场局域化难题.

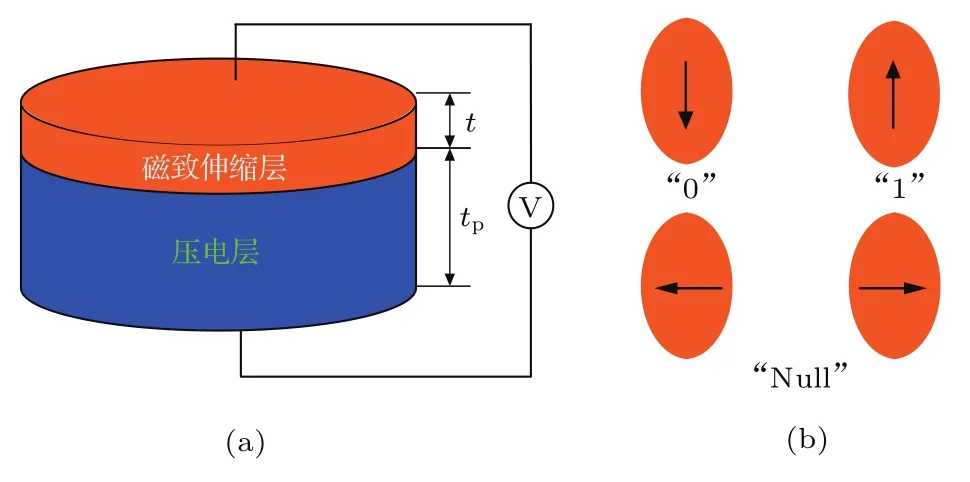
图1 (网刊彩色)NMLD (a)多铁纳磁体;(b)逻辑态Fig.1.(color online)NMLD:(a)Multiferroic nanomagnet;(b)logic states.

拉长的纳磁体具有明显的形状各向异性,可以用来表征二值信息,如图1(b)所示.拉长纳磁体长轴(易磁化轴)表征逻辑态“0”或“1”,而短轴(难磁化轴)则表征逻辑“空”.通过纳磁体不同的排列方式,可以实现逻辑信息在纳磁体器件中的定向传递,如铁磁耦合互连线[6]、反铁磁耦合互连线[14]、择多逻辑门[17]等.文献[17]建立了基于多铁逻辑的择多逻辑门二维模型,该研究仅考虑了纳磁体的面内磁化,忽略了面外磁化对择多逻辑门磁化翻转的影响,因而所获磁化动态及转换特性是不准确的.实际上,面外磁化在纳磁体磁化动态翻转中起着关键作用,纳磁体的磁化翻转是面内磁化和面外磁化共同作用的结果.本文对多铁择多逻辑门的转换特性进行了深入研究,建立了择多逻辑门的三维磁化动态模型,并对择多逻辑门的择多计算功能进行了仿真,进一步分析了应变时钟的工作机制,找到了如何有效控制择多逻辑门正确工作的一些准则.

2 多铁择多逻辑门三维磁化动态模型

CMOS技术中的基本电路是反相器,而NMLD技术的基本电路却是择多逻辑门[18].在NMLD技术中,择多逻辑门由五个纳磁体组成,其结构如图2(a)所示,I1,I2,I3为输入纳磁体;C为中心纳磁体(完成择多计算);O为输出纳磁体.由纳磁体构成的择多逻辑门逻辑功能函数为

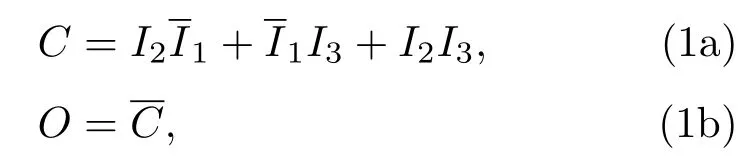
从(1)式可以获得该择多逻辑门工作的真值表,如表1所列.

从表1可以看出,该择多逻辑门真值表与常规择多逻辑门真值表的差别在于本文择多逻辑门模型是从中择多输出,而常规择多逻辑门则是从I1,I2,I3中择多输出.造成该差别的原因是本文择多逻辑门I1和C二者是反铁磁耦合,磁化反平行排列,C接受到的逻辑实际为两类择多逻辑门本质上没有区别,在I1和C之间增加一个纳磁体,就可以实现常规择多逻辑门计算功能.

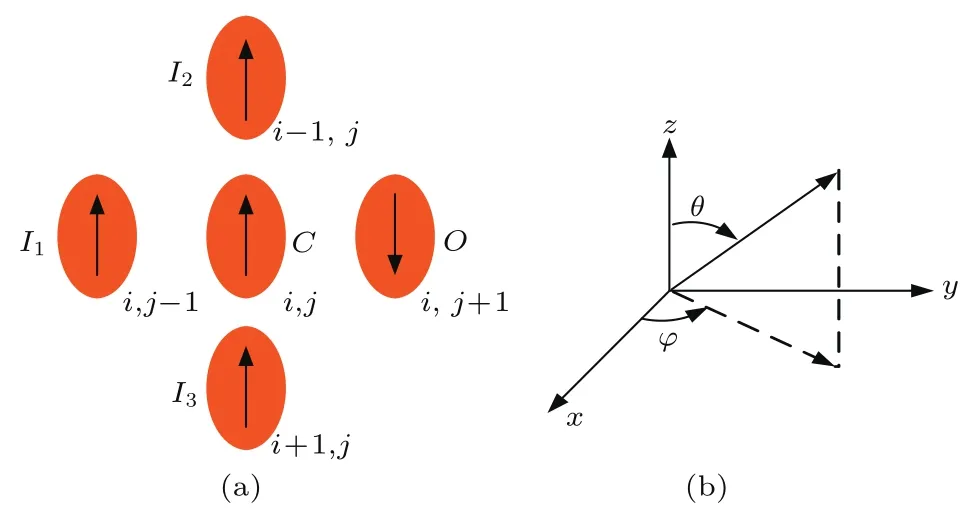
图2 (网刊彩色)纳磁体逻辑门 (a)择多逻辑门;(b)坐标轴分配Fig.2.(color online)Nanomagnet logic gate:(a)Majority gate;(b)axis assignment.

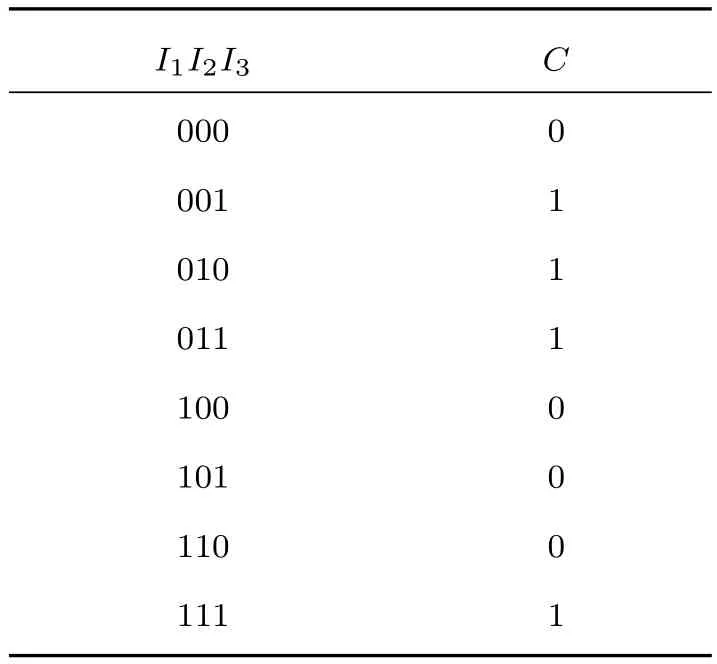
表1 择多逻辑门真值表Table 1.The truth table of Majority gate.

假设纳磁体磁化的极角(面外)和方位角(面内)分别是θ和φ,在y-x平面内,y轴指向纳磁体易磁化轴,x轴指向纳磁体难磁化轴,而z轴反映了纳磁体厚度,坐标分配以及极角和方位角定义如图2(b)所示.因而,逻辑“0”表示φ=−90°,逻辑“1”表示φ=90°,逻辑“空”表示φ=0°.

铁磁耦合[6]和反铁磁耦合[14]分别在C上产生的偶极子耦合能为

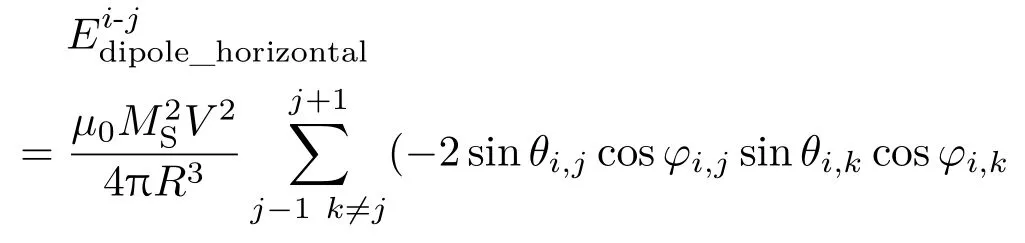
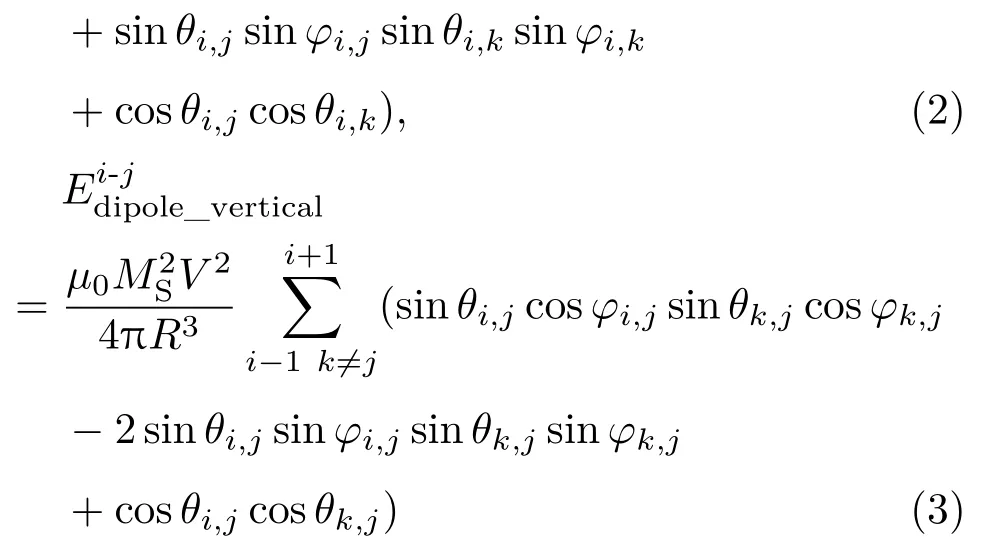
(2)和(3)式中µ0是真空磁导率,MS是饱和磁矩,V是纳磁体体积,R是相邻纳磁体中心间距.基于(2)和(3)式,推导出C上总的偶极子耦合能为其中分别为

而任一纳磁体形状各向异性能Eshape_anisotropy为[19]

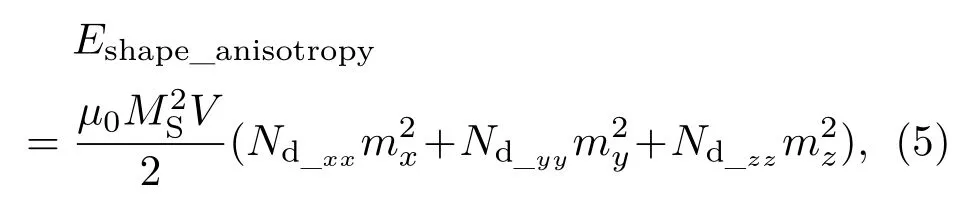
Nd_xx,Nd_yy和Nd_zz分别是沿着三个坐标轴的退磁系数.假设磁层是椭圆形薄膜,椭圆的长轴和短轴分别为a,b,薄膜厚度为t,则退磁系数计算如下[19]:

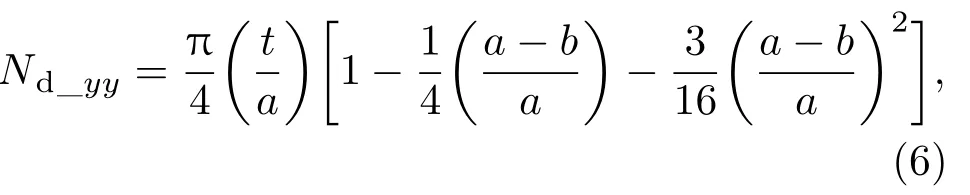
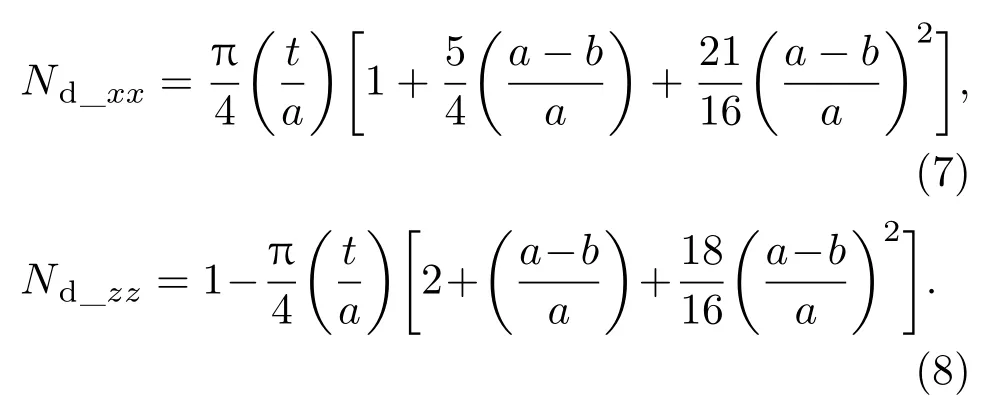
纳磁体在应力/电压作用下产生的应力各向异性能Estress_anisotropy为[14]

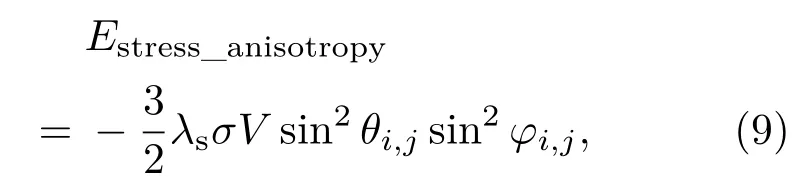
其中3λs/2为饱和磁致伸缩,σ为施加的应力值.因此,任一单畴纳磁体的总能量E可以表示为多铁纳磁体逻辑器件的磁化动态可以用Landau-Lifshitz-Gilbert(LLG)方程描述如下[20](阻尼系数α≤1):

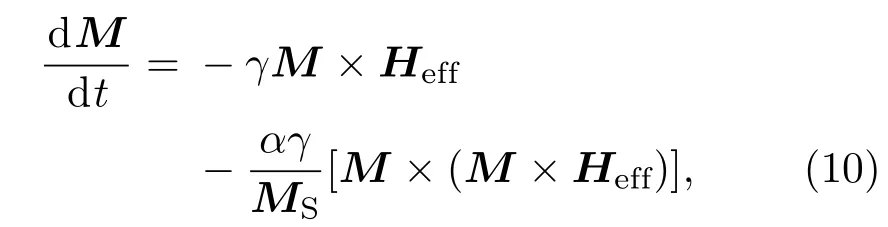
其中M是多铁纳磁体的磁矩矢量,α是阻尼系数,γ是回磁比.Heff是任一纳磁体上的有效场,该有效场作用在纳磁体上产生了磁矩(M×Heff),使得纳磁体的磁化发生翻转,其表达式为[20]

Hdipole,Hshape,Hstress分别为偶极子耦合能、形状各向异性能、应力各向异性能产生的有效场分量.外界随机性热涨落的影响可以通过一个随机热场h(t)来描述,hi(t)是热场沿着坐标轴的分量,可以写为[21]

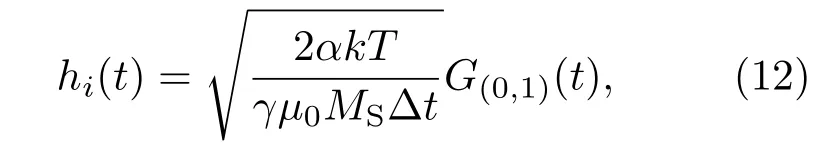
其中k是玻尔兹曼常数,T是当前室温,1/Δt是热噪声的振荡频率,G(0,1)(t)表示均值为0,方差为1的高斯分布函数.基于(11)和(12)式,推导出有效场沿着各个坐标轴的分量分别如下:

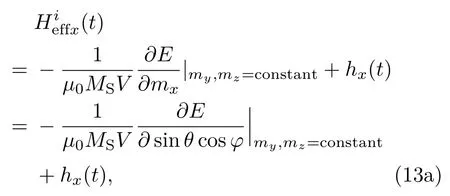
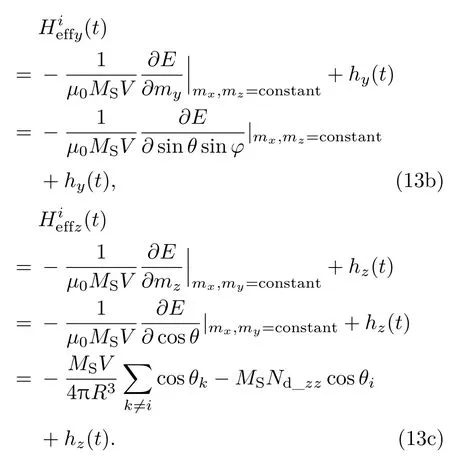
将磁矩矢量M对饱和磁矩MS归一化处理:

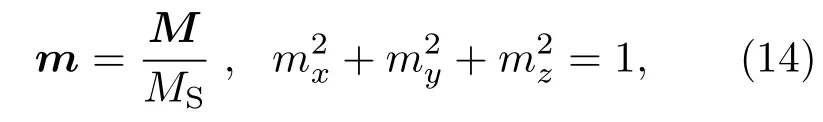
mx,my,mz是归一化磁矩矢量m沿坐标系的三个分量,可用参数方程表示如下:

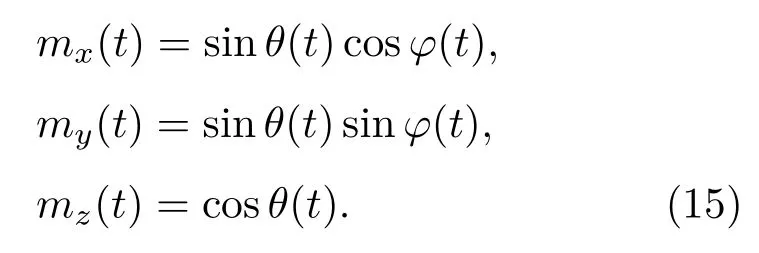
将(15)式代入(10)式,化简LLG方程得到两个联立的微分方程,可以确定任一纳磁体的极角θ和方位角φ的动态变化:

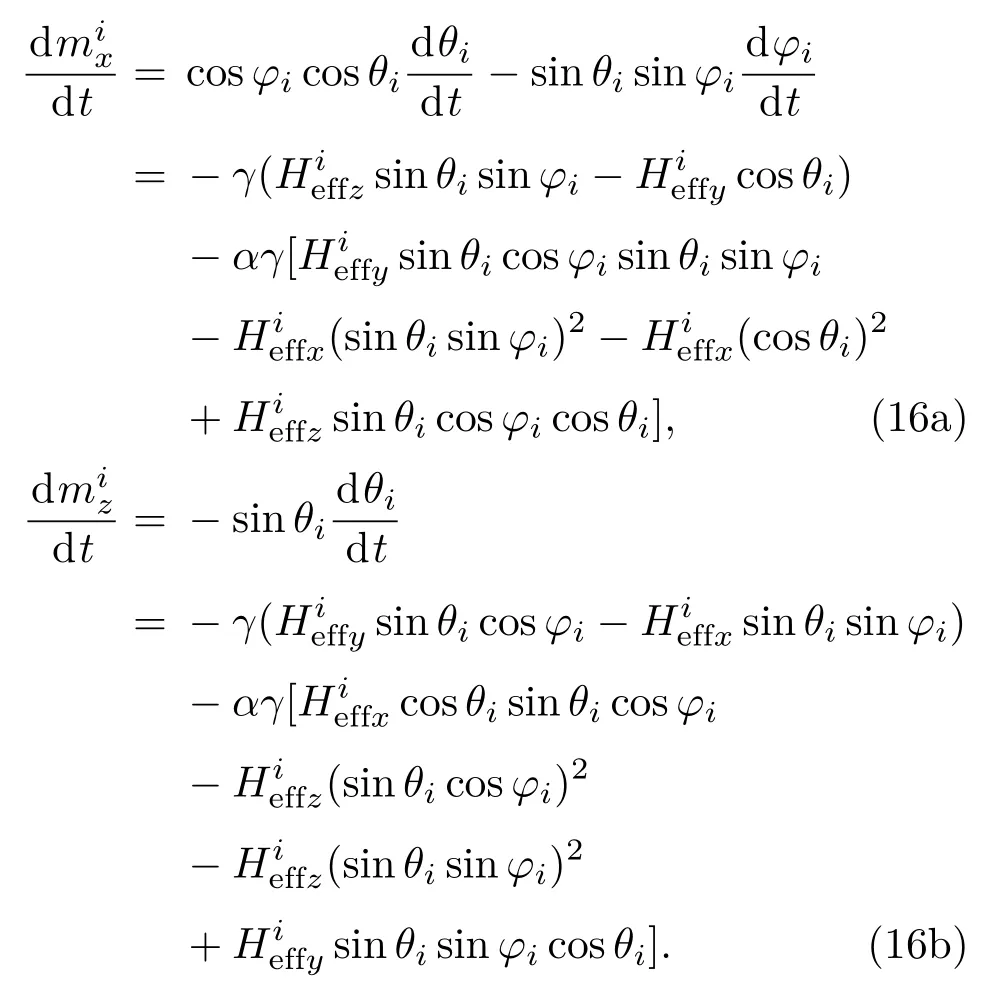
将(13)式代入(16)式,推导得到多铁纳磁体择多逻辑门三维磁化动态模型,可求解多铁择多逻辑门输出纳磁体及中心纳磁体的磁化动态.通过改变相关参数,观察这些参数对择多逻辑门计算功能及动态特性的影响.

3 多铁纳磁体择多逻辑门的磁化动态模拟

3.1 接受新输入的择多计算功能仿真

采用四阶龙格-库塔方法对(16)式进行数值求解,可以求出任一纳磁体(除输入外)任意时刻的极角和方位角数值.压电层材料为PMN-PT,磁层材料为Terfenol-D.磁层各参数如表2所列.

表2 磁层材料Terfenol-D参数Table 2. The parameters of magnetic material Terfenol-D.

仿真中用到的其他参数:R=200 nm,压电层厚度tp=40 nm.上述参数的选择可以确保纳磁体在逻辑态和空态之间的形状各向异性能势垒为0.8 eV,这足以抵抗外界随机热涨落引起的自发磁化翻转.同时,偶极子耦合能为0.26 eV,这也防止纳磁体磁化在未施加应力时发生自发翻转.纳磁体尺寸可以进一步缩小,但要确保纳磁体逻辑态和空态之间的形状各向异性能势垒能够抵抗外界热噪声的影响,同时相邻纳磁体之间的耦合作用不足以使纳磁体磁化发生翻转.仿真过程采用的是流水线式班尼特时钟[8],I1,I2,I3的初始态为“000”,C和O的初始态为“11”.为了观察择多逻辑门的动态翻转,给C施加30 MPa的应力(相当于给图1(a)加150 mV的电压),直到0.386 ns后撤去该应力;0.02 ns后给O施加30 MPa的应力,直到0.6 ns后撤去该应力,观察择多逻辑门C和O的终态.当I1,I2,I3接受到新的逻辑信息,输入组合依次变为逻辑“001”和“101”,对C和O施加上述应变时钟,观察所建择多逻辑门三维磁化动态模型能否实现正确的择多计算功能.重点观察C的磁化翻转情况,因为C用于接受输入,完成择多计算.根据表1,当输入为“000”时,C的磁化应为逻辑“0”;当输入为“001”时,C的磁化应为逻辑“1”;当输入为“101”时,C的磁化应为逻辑“0”(从文献[22]中可知,由于随机热涨落的影响,磁化和易磁化轴之间存在5°的偏差,因而逻辑“0”实际表示φ=−85°,而逻辑“1”实际表示φ=85°. 特别地,极化角θ=89.9°).择多逻辑门接受新输入仿真结果如图3所示.

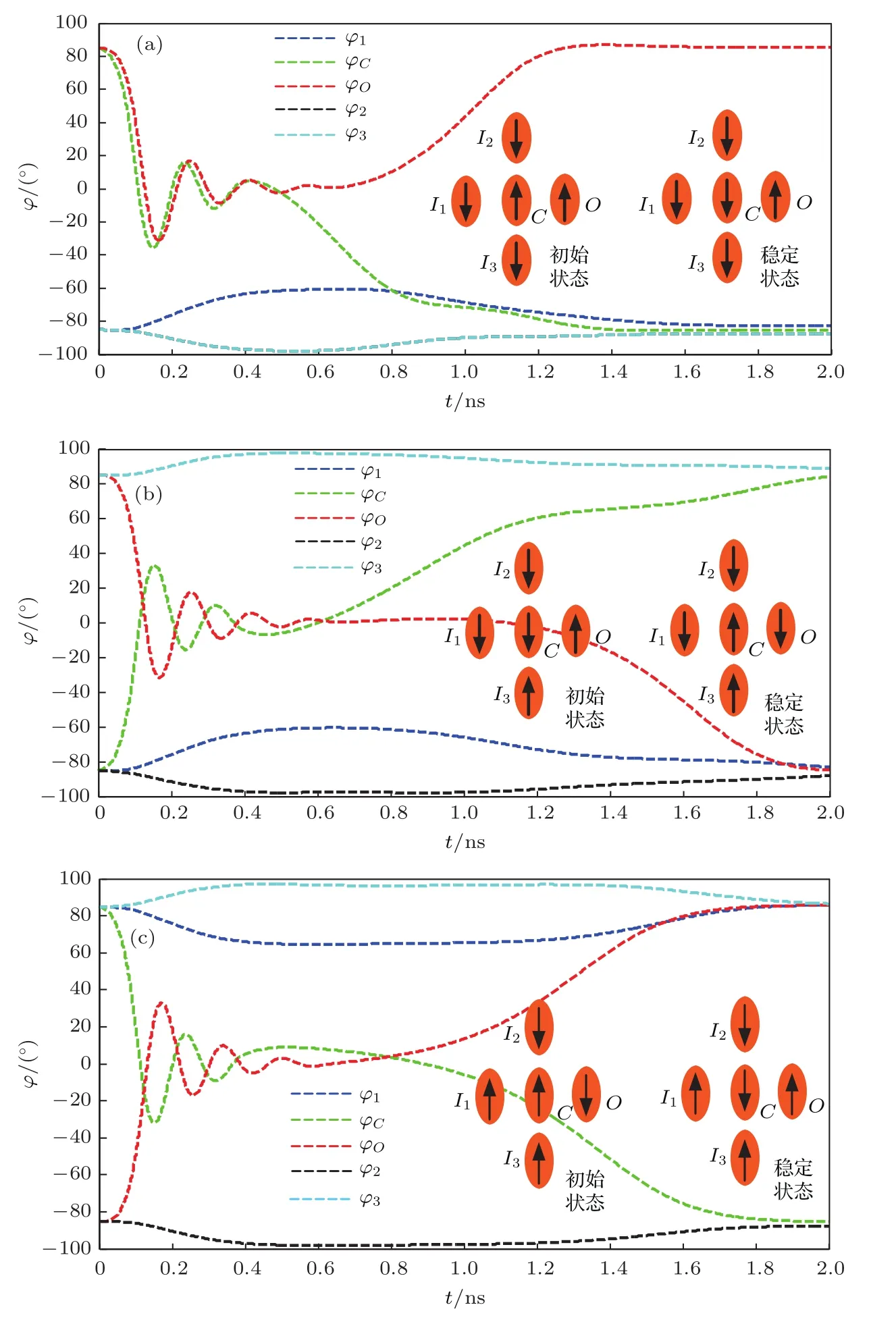
图3 (网刊彩色)择多逻辑门仿真结果 (a)初始输入“000”;(b)输入变化为“001”;(c)输入变化为“101”Fig.3.(color online)Simulation results of magnetization dynamics of Majority gate:(a)Initial input “000”(b)“001” then;(c)“101” then.

从图3(a)可见,I1,I2,I3初始态是“000”,施加应变时钟后,C的磁化在应力的作用下翻转到了逻辑“空”,当应力撤去以后,C在I1,I2,I3的偶极子耦合作用下,正确地翻转到逻辑“0”.之后I3接受到新的输入,从逻辑“0”翻转到逻辑“1”,择多逻辑门的磁化翻转如图3(b)所示,此时I1,I2,I3的状态为“001”,而C的初始态为逻辑“0”,施加上述应变时钟后,C从逻辑“0”正确地翻转到了逻辑“1”.从图3(b)也可以看出来,虽然没有对I1,I2,I3施加应变时钟,但是纳磁体之间的偶极子耦合能产生的Hdipole以及形状各向异性能产生的Hshape,使得I1,I2,I3的磁化在面内以及面外都会发生一定角度的偏转,并随着C的稳定而稳定下来.为了直观地看出这一过程,图4给出了I1磁化翻转的三维轨迹,I1产生了面内和面外的磁化偏转,由于形状各向异性能较高,偶极子作用诱导的自发翻转被抑制,因而纳磁体磁化回到初始状态,产生如图4的磁化动态变化,I2,I3与I1情况类似.C在铁磁和反铁磁耦合作用的叠加下,其磁化从逻辑“0”正确地翻转到逻辑“1”(φC=83.8°). 如图5所示,C的磁化翻转是面外磁化和面内磁化相互竞争的结果,施加应力以后,面外各向异性较大,在磁化翻转过程中,面外磁化占优,因而存在较大的面外极化角(θC的变化范围为84.1°—103.3°). 随着应力的持续作用,磁化逐渐翻转到逻辑“空”,此时,沿着难磁化轴的面内各向异性占优,而面外各向异性较弱,存在轻微的面外磁化(θC的变化范围为88.7°—93.9°).应力撤去以后,沿面内易磁化轴的各向异性占优,而面外各向异性几乎为0,面外极角较为稳定(约90.13°),磁化逐渐翻转到逻辑“1”.图5(c)给出了C磁化翻转的三维曲线,该曲线详细描述了C复杂的磁化动态.

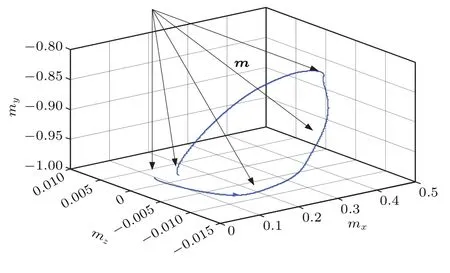
图4 (网刊彩色)输入纳磁体I1磁化翻转的三维图像Fig.4.(color online)Three-dimensional plot of magnetization dynamics of the input nanomagnet I1.

O在与C的反铁磁耦合作用下,从逻辑“1”正确地翻转到逻辑“0”(φO=−84.9°). 当择多逻辑门的输入I1再次接受到新的逻辑输入,从逻辑“0”翻转到逻辑“1”,此时输入I1,I2,I3的状态变为“101”,C的初始态为逻辑“1”,施加上述应变时钟后,C的磁化从逻辑“1”正确地翻转到了逻辑“0”,如图3(c)所示.从这个仿真可以看出,当输入I1,I2,I3的逻辑态从“000”变化到“001”再到“101”,相应地,C的磁化从逻辑“0”翻转到逻辑“1”再翻转到逻辑“0”,仿真结果与表1是相符的.这表明在合适的应变时钟下,建立的择多逻辑门三维磁化动态模型实现了正确的择多计算功能,当输入发生变化时,也能正常工作.由纳磁体构成的该择多逻辑门从理论上是可以实现的.

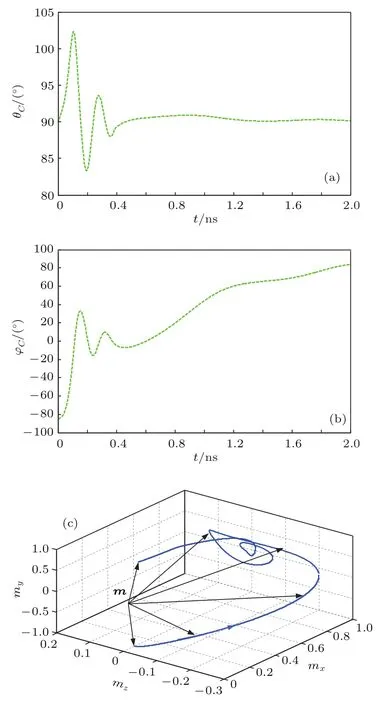
图5 (网刊彩色)择多逻辑门中心纳磁体C磁化动态(a)极角;(b)方位角;(c)三维轨迹Fig.5.(color online)Magnetization dynamics of the cental nanomagnet C of Majority gate:(a)Polar angle(b)azimuthal angle;(c)three-dimensional trajectory.

3.2 应变时钟影响择多逻辑门择多计算功能

为了探究应变时钟对择多逻辑门计算功能的影响,改变作用于O上应力的持续时间,观察择多逻辑门的磁化动态特性,这里仿真输入为“111”时的动态特性,其他输入组合可以类比仿真.开始给C施加30 MPa的应力,直到0.386 ns后撤去应力;0.02 ns以后给O施加30 MPa的应力,分别仿真0.386,0.4,0.46,0.5,0.6,0.9,1.3,1.9 ns后撤去O上的应力,择多逻辑门的工作情况.此时,作用于C和O上应力撤去的间隔分别为0,0.014,0.074,0.114,0.214,0.514,0.914,1.514 ns.仿真结果见表3.

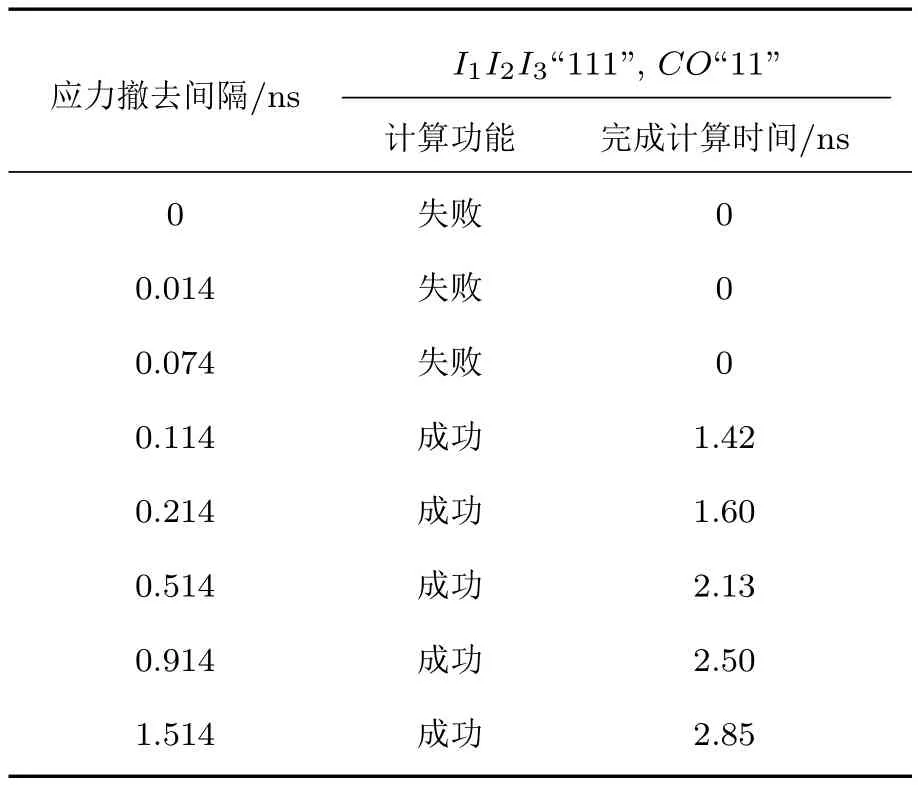
表3 不同应变时钟下择多逻辑门动态仿真结果Table 3.The simulation results of Majority gate under different strain clock.

从表3可以看出,过早撤去O上的应力(应力撤去间隔小于0.1 ns),择多逻辑门计算功能出现错误(计算完成时间为0 ns).这是因为,O需要根据C的逻辑态确定正确的翻转方向,由于两者是反铁磁耦合,当C的磁化翻转为逻辑“1”时,O的磁化应当翻转为逻辑“0”.提前撤去应力,C没有及时翻转到预期的逻辑态,二者的耦合作用不足以使O的磁化实现正确的翻转.这个仿真结果表明,应力撤去间隔小于0.1 ns会降低择多逻辑门工作的正确率,而应力撤去间隔大于0.2 ns则会降低择多逻辑门的工作频率,所以当输入为“111”时,最优应力撤去间隔为0.1—0.2 ns.由于不同输入下C和O的磁化运动曲线不同,为了找到择多逻辑门工作的最优应力撤去间隔,图6给出了所有输入下择多逻辑门完成计算时间的仿真结果.

图6中计算完成时间为0 ns表示择多逻辑门计算失败,从图中可以看出,当应力撤去间隔小于0.1 ns时,择多逻辑门出现计算错误;当应力撤去间隔大于0.2 ns时,计算完成时间明显上升.虽然在不同输入条件下,择多逻辑门工作的最优撤去间隔有差异,但是对于择多逻辑门而言,需要确保8种输入下的计算正确率和工作频率,因此最优撤去时间间隔仍为0.1—0.2 ns.

图7表示输入为“111”,应力撤去间隔为0.014 ns时,O的磁化翻转情况.从图7可以清楚地看出来,O的磁化从逻辑“1”翻转到逻辑“空”,最后翻转失败又回到逻辑“1”的整个过程.

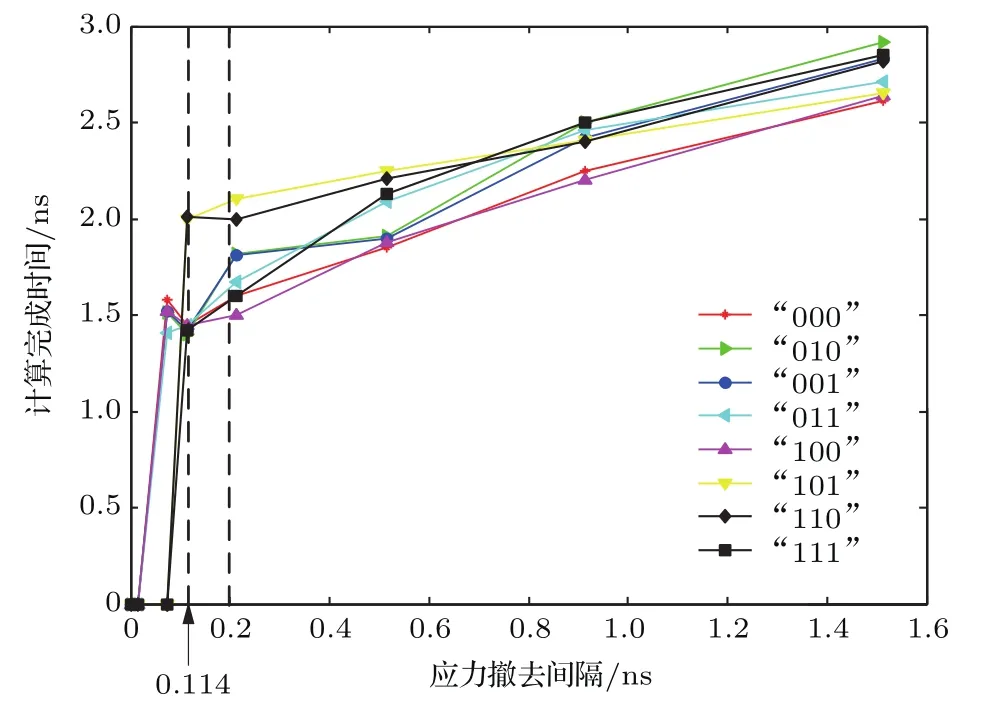
图6 (网刊彩色)择多逻辑门不同输入下计算完成时间仿真结果Fig.6.(color online)The simulation results of computing time of majority gate under different inputs.

图7 (网刊彩色)择多逻辑门输出纳磁体O磁化翻转的三维图像Fig.7.(color online)Three-dimensional plot of magnetization dynamics of the output nanomagnet O of majority gate.

4 结 论

本文建立了多铁择多逻辑门三维磁化动态模型,利用数值计算方法对择多逻辑门磁化翻转动态过程进行了深入的模拟研究,并对试验结果进行了理论分析.研究重点关注择多逻辑门接受新输入后的动态特性,同时对应力持续时间产生的影响进行了探索.研究结果表明:建立的三维磁化动态模型准确地描述了择多逻辑门的动态特性,在合适的应变时钟(30 MPa)下,择多逻辑门能够接受新逻辑完成择多计算功能;当应力撤去间隔小于0.1 ns时,择多逻辑门会出现错误的工作状态,这是因为提前撤去应力,纳磁体之间的耦合作用还不足以克服形状各向异性能,因而容易出现错误;当应力撤去间隔大于0.2 ns,择多逻辑门的工作频率会下降,这是因为择多逻辑门一直处于逻辑“空”,没有进行择多计算.输出纳磁体上应力撤去时机应为中心纳磁体时钟撤去后0.1—0.2 ns之间,这样可确保择多逻辑门正确转换概率及工作频率.

[1]Cowburn R P,Welland M E 2000Science287 1466

[2]Csaba G,Imre A,Bernstein G H,Porod W,Metlushko V 2002IEEE Trans.Nanotechnol.1 209

[3]Vacca M,Graziano M,Crescenzo L D,Chiolerio A,Lamberti A,Balma D,Canavese C,Celegato F,Enrico E,Tiberto P,Boarino L,Zamboni M 2014IEEE Trans.Nanotechnol.13 963

[4]Imre A,Csaba G,Ji L,Orlov A,Bernstein G H,Porod W 2006Science311 205

[5]Niemier M T,Bernstein G H,Dingler A,Hu X S,Kurtz S,Liu S,Nahas J,Porod W,Siddiq M,Varga E 2011J.Phys.:Condens.Matter23 493202

[6]Yang X K,Zhang B,Cui H Q,Li W W,Wang S 2016Acta Phys.Sin.65 237502(in Chinese)[杨晓阔,张斌,崔焕卿,李伟伟,王森2016物理学报65 237502]

[7]Tiercelin N,Dusch Y,Klimov A,Giordano S,Preobrazhensky V,Pernod P 2011Appl.Phys.Lett.99 192507

[8]Atulasimha J,Bandyopadhyay S 2010Appl.Phys.Lett.97 173105

[9]Zhang N,Zhang B,Yang M Y,Cai K M,Sheng Y,Li Y C,Deng Y C,Wang K Y 2017Acta Phys.Sin.66 027501(in Chinese)[张楠,张保,杨美音,蔡凯明,盛宇,李予才,邓永城,王开友2017物理学报66 027501]

[10]Alam M T,Kurtz S J,Siddiq M A J,Niemier M T,Bernstein G H,Hu X S,Porod W 2012IEEE Trans.Nanotechnol.11 273

[11]Zhang M L,Cai L,Yang X K,Qing T,Liu X Q,Feng C W,Wang S 2014Acta Phys.Sin.63 227503(in Chinese)[张明亮,蔡理,杨晓阔,秦涛,刘小强,冯朝文,王森2014物理学报63 227503]

[12]Bhowmik D,You L,Salahuddin S 2014Nat.Nanotechnol.9 59

[13]Ralph D C,Stiles M D 2008J.Magn.Magn.Mater.320 1190

[14]Fashami M S,Roy K,Atulasimha J,Bandyopadhyay S 2011Nanotechnology22 155201

[15]Souza N D,Fashami M S,Bandyopadhyay S,Atulasimha J 2016Nano Lett.16 1609

[16]Biswas A K,Ahmad H,Atulasimha J,Bandyopadhyay S 2017Nano Lett.17 3478

[17]Yilmaz Y,Mazumder P 2013IEEE Trans.VLSI Syst.21 1181

[18]Yang X K,Cai L,Kang Q,Bai P,Zhao X H,Feng C W,Zhang L S 2011Acta Phys.Sin.60 098503(in Chinese)[杨晓阔,蔡理,康强,柏鹏,赵晓辉,冯朝文,张立森2011物理学报60 098503]

[19]Chikazumi S 1964Physics of Magnetism(New York:Wiley)p25

[20]Fidler J,Schre flT 2000J.Phys.D:Appl.Phys.33 R135

[21]Brown W F 1963Phys.Rev.130 1677

[22]Fashami M S,Roy K,Atulasimha J,Bandyopadyay S 2011Nanotechnology22 309501

PACS:75.78.—n,85.70.Kh,85.80.Jm DOI:10.7498/aps.66.217501

*Project supported by the National Natural Science Foundation of China(Grant No.11405270)and the Scienti fi c Research Foundation for Postdoctor of Air Force Engineering University,China(Grant Nos.2015BSKYQD03,2016KYMZ06).

†Corresponding author.E-mail:qianglicai@163.com

Three-dimensional magnetization dynamics in majority gate studied by using multiferroic nanomagnet∗

Wei Bo Cai Li†Yang Xiao-Kuo Li Cheng

(Science College,Air Force Engineering University,Xi’an 710051,China)

d 27 May 2017;revised manuscript

25 July 2017)

The scaling of traditional complementary metal oxide semiconductor(CMOS)device is reaching its physical limit,and alternative emerging devices are being explored as possible CMOS substitutes.One of the most promising device technologies is nano-magnetic logic(NML),which is an energy-efficient computing paradigm.The inherent nonvolatility and low energy consumption make NML device possess wide application perspectives.The basic element of multiferroic NML is a sub-100 nm sized single domain magnet.Generally,thex-yplane determines the in-plane dimension,while thezdirection indicates the thickness of nanomagnet.Classical binary logic states “0”and “1”are encoded in two stable magnetization orientations along the easy axis(major axis)of the elliptical nanomagnet,while the hard axis(minor axis)refers to “null”logic.In order to propagate logic bits between the neighbor nanomagnets,one requires a clock that periodically fl ips every magnet’s magnetization along the hard axis simultaneously,and the dipole-dipole interaction between the neighbors will force the magnet into the correct orientation along the easy axis,and thus the logic bit propagates unidirectionally.In multiferroic NML,the majority gate is a basic element of nanomagnet logcal circuit.In this paper,the three-dimensional switching dynamic model of a multiferroic nanomagnetic majority gate is established,and its magnetization dynamics is simulated by solving the Landau-Lifshitz-Gilbert equation with considering the thermal fl uctuation effects.The majority gate is implemented with dipole-coupled two-phase(magnetostrictive/piezoelectric)multiferroic elements and is simulated by using different strain clocks and changing the input.It is found that the majority gate works efficiently and correctly when receiving new input.It is also found that the optimal time interval of stress releasing between central nanomagnet and output nanomagnet is 0.1–0.2 ns.Removing stress earlier will reduce the success rate of the majority gate operation while the work frequency increases.The reason behind the phenomenon may be that removing stress earlier results in weak dipole-coupled interaction,which cannot overcome the shape anisotropy.These findings are bene fi cial to the design of multiferroic logic circuit.

multiferroic nanomagnet,majority gate,strain clock,magnetization dynamics

建立了多铁纳磁体择多逻辑门的三维磁化动态模型,并施加应变时钟(应力或电压)对多铁择多逻辑门的择多计算功能进行了动态仿真,同时分析了应变时钟工作机制以及它与择多逻辑门可靠转换之间的关系.仿真结果表明所建三维动态模型准确地描述了择多逻辑门的工作机制,在30 MPa应力作用下,择多逻辑门接受新输入实现了正确的择多计算功能.研究还发现对中心纳磁体和输出纳磁体依次撤去应变时钟时,提前撤去输出纳磁体上的应力会降低择多逻辑门的正确计算概率,而延迟撤去输出纳磁体上的应力会降低择多逻辑门的工作频率.研究结果深化了人们对多铁择多逻辑门动态特性的认识,可为多铁逻辑电路的设计提供重要指导.

10.7498/aps.66.217501

∗国家自然科学基金(批准号:11405270)和空军工程大学理学院博士后科研启动基金(批准号:2015BSKYQD03,2016KYMZ06)资助的课题.

†通信作者.E-mail:qianglicai@163.com

©2017中国物理学会Chinese Physical Society