航空发动机管路流固耦合振动的固有频率分析

李占营，王建军，邱明星

（1.北京航空航天大学能源与动力工程学院，北京100191；2.中国航发沈阳发动机研究所，沈阳110015）

航空发动机管路流固耦合振动的固有频率分析

李占营1，王建军1，邱明星2

（1.北京航空航天大学能源与动力工程学院，北京100191；2.中国航发沈阳发动机研究所，沈阳110015）

为研究流体哥氏力和管路参数等因素对航空发动机管路固有振动频率的影响规律，采用G alerkin方法建立了管路流固耦合数学模型，并通过复特征值分析得到了系统的固有频率。通过将采用G alerkin方法的计算结果与试验测试数据进行比较，验证了G alerkin方法的正确性；给出了试验管路的临界流速，并研究了流体哥氏力和管路截面尺寸对系统固有频率的影响。结果表明：试验燃油管路实际流速远小于发生屈曲失稳的临界流速；哥氏力对不锈钢和钛合金2种管材燃油管路固有频率的影响很小；相同壁厚管路，外径越小，流固耦合对固有频率的影响越大。

输液管路；流固耦合；G alerkin方法；固有频率；哥氏力；航空发动机

0 引言

航空发动机管路系统用于发动机部件之间及其与飞机间的流体输送。管路系统振动会引发管路故障，影响到管路系统甚至发动机安全可靠地运行。该振动属于典型的输液管路振动，而作为振动的前沿课题，国内外很多学者[1-3]采用不同方法对输液管路的动力学行为进行了深入研究。Holmes[4]利用Lyapunov直接法研究了两端固支输液直管在自激励作用下全局动态行为，表明该类管路不会发生颤振失稳；张智勇[5]采用传递矩阵法研究了流固耦合对输液管路固有频率的影响；金基铎[6]采用平均法研究了两端固支输液直管在脉动内流作用下的参数共振问题；Tornabene[7]采用广义微分求积法研究了输液直管的临界流速。

在固有振动特性研究方面，杨晓东等[8]以复模态分析方法为基准，研究了Galerkin截断方法对两端铰支输液管路固有频率分析的精确性；齐欢欢等[9]采用Galerkin离散和复模态2种方法计算了不同流速下悬臂输液管的固有频率；杨超等[10]采用特征线法研究了管道结构阻尼、管材泊松比、管道壁厚以及管道材料等参数对蓄水池-管道-阀门系统声弹耦合振动特性的影响；Lin等[11]采用复模态法研究了基础激励下航空发动机液压直管的流固耦合振动，得出了流体压力、流速和轴向力的增加，会引起管路固有频率降低的结论；Huang等[12]基于Ferrari法，推导出两端支承输液管路固有频率方程，并研究了两端支承输液直管的固有频率和稳定性；Wang等[13]采用有限元法基于ADINA建立输液管路3维流固耦合动力学模型，计算了直管和曲管的固有频率，并与解析法进行了对比。

从现有的研究工作可见，输液管路固有振动特性的研究主要集中在研究管路的临界流速，以及流体压力、流速等因素对固有频率的影响，还未发现由流体引起的哥氏力对固有频率影响的研究。

本文采用Galerkin方法建立输液管路系统的流固耦合动力学模型，计算并试验验证燃油管路流固耦合固有频率，研究其临界流速及哥氏力和管路外径对输液管路固有频率的影响规律。

1 管路系统流固耦合模型

1.1 研究对象

研究对象为两端固支的输液管路系统，如图1所示。模型两端固定约束，流体从左端流入、右端流出。管路的长度和抗弯刚度分别为L和EI，其中E为弹性模量、I为管路截面惯性矩。管内流体的平均流速为U。

1.2 运动方程及其离散特性

假定管内为无黏不可压缩的稳定流动流体，忽略重力、阻尼力、管路轴向载荷和管内流体压力，并对管路采用小变形假设，由牛顿力学原理，得到管路微段的运动微分方程[14]

式中：w、x、t、mp、mf分别为管路横向位移、管路横截面所处的位置、时间、管路线密度、管内流体线密度，各项的物理意义分别为弹性恢复力、离心力、哥氏力和惯性力。

两端固支边界条件为

引入

得到无量纲方程

其中

则无量纲边界条件为

考虑定常流，采用4阶Galerkin方法对式（4）进行离散，即令

式中：φ（rξ）、q（rτ）分别为相同边界条件梁的无量纲振型函数、离散系统广义坐标。

将式（7）代入式（4），左乘 φ（rξ），并在[0,1]区间内积分，同时利用正弦函数的正交性（即δsr是 Kronecker’s delta函数）及，得到离散后的系统微分方程

式中：s=1,2,…,4；λr为两端固支梁无量纲特征值；bsr=

式（8）可以写成如下矩阵形式

式（9）可以写成标准形式

由于哥氏力矩阵B的存在，使得系统阻尼矩阵[C]为反对称矩阵，因此只能采用复特征值方法求解式（10）的特征值。首先引入状态方程，将式（10）特征值问题转换为标准特征值问题，再进行求解。

2 输液管路的固有频率试验

对两端固支燃油管路进行固有频率测试，将试验测试结果与采用Galerkin方法的计算结果进行对比。

燃油钛合金直管的固有频率测量采用锤击法[15]。试验设备包括加速度计、力锤、INV303系列智能信号采集处理分析仪、计算机及DASP大容量数据采集与信号处理分析软件。锤击法对燃油管路进行振动测试如图2所示。

试验件管长1000 mm，厚1 mm，外径为14 mm。采用台钳夹紧管路两端，近似实现固支约束。约束位置点距离导管两端100 mm。

数值计算采用Galerkin方法进行建模，模型中管路材料的弹性模量、泊松比和密度分别取96 GPa、0.39 和 4470 kg/m3，燃油密度取其20℃时的密度值802.4 kg/m3。两端固支空管的前2阶固有频率见表1。

从表中可见，燃油管路的前2阶固有频率数值计算结果与试验结果比较吻合。相对误差在3%以内，因此Galerkin方法的计算精度得到了验证，计算值与试验值的差异原因在于台钳夹紧不能实现完全固支边界条件。

不同流速下两端固支燃油管路的第1阶固有频率见表2。

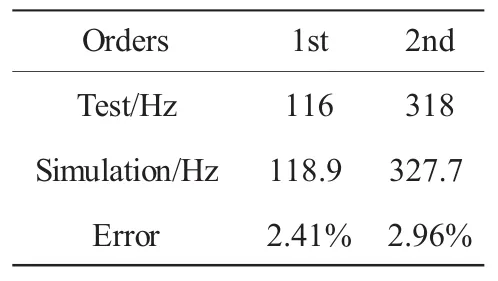
表1 两端固支空管的固有频率

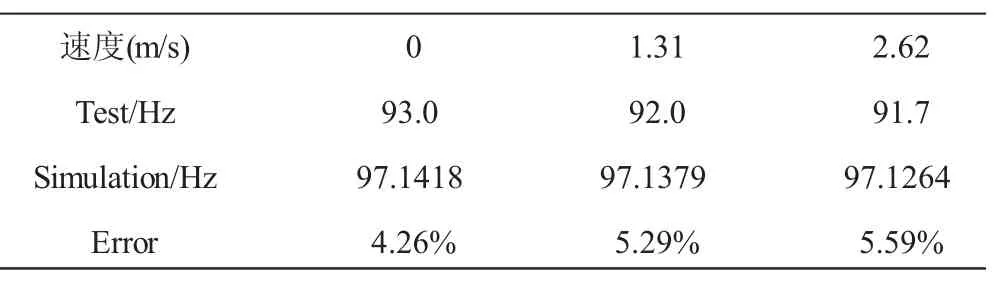
表2 不同流速两端固支燃油管路的固有频率

从表中可见，计算结果与试验结果比较吻合，随着流速的增加第1阶固有频率均减小；燃油流速在2.62 m/s以下时，管路的第1阶固有频率减小的幅值很小，这是因为此时的无量纲流速仅为0.0692；计算结果与试验结果的相对误差为4.26%～5.59%，差异的原因在于试验不能实现计算中假设的完全固支边界条件。

3 临界流速及固有频率分析

3.1 临界流速分析

采用4阶Galerkin离散方法建立试验管路的数学模型，计算其特征值问题，得到试验管路固有频率随流速变化的规律，如图3所示。

从图中可见，随着流速的增加，管路的刚度减小，固有频率降低，这与现有文献的研究结论一致[14]；试验管路的临界流速为150 m/s,实际发动机燃油管路流速远小于这一流速，因此不会发生屈曲失稳。

3.2 哥氏力对固有频率的影响

之后，通过计算研究哥氏力对管路系统固有频率的影响规律。燃油流速在100m/s之内，是否考虑哥氏力时管路系统的固有频率及相对误差分别如图4、5所示。

从图5中可见，燃油流速在100 m/s以内时，忽略哥氏力引入误差随着流速的增加而增加，但最大误差不超过1.5E-3。这说明哥氏力对钛合金燃油管路前2阶固有频率的影响几乎可以忽略。这是因为由燃油流速引起的哥氏力对阻尼矩阵的改变很小，从而使管路系统的阻尼固有频率和无阻尼固有频率几乎相同。

相同截面尺寸的不锈钢管路是否考虑哥氏力时的固有频率及相对误差分别如图6、7所示。

从图6、7中可见，与钛合金燃油管路的规律相同，即随着流速增加，管路刚度减小，固有频率降低；忽略哥氏力得到的固有频率最大误差不超过5E-4。另外，与钛合金管路相比，不锈钢质量增加对固有频率的影响小于截面刚度增加对固有频率的影响，因此，不锈钢管路的固有频率大于相同截面尺寸钛合金管路的。

3.3 管路外径对固有频率的影响

壁厚为1 mm，外径分别为20、14和8 mm的两端固支钛合金燃油管路第1阶固有频率随流速的变化规律如图8所示。在不同外径下，流速对钛合金管路固有频率影响的相对变化情况如图9所示。

从图8、9中可见，相同壁厚管路在相同流速下：

（1）随着外径的增大，钛合金燃油管路的固有频率升高。这是因为通过增大管路外径，系统刚度增大，进而固有频率提高。

（2）随着外径的增大，相对于流速为零时的固有频率变化率减小，这说明流固耦合对于直径小的管路影响更大。例如，在流速为100 m/s时，外径为8 mm的管路固有频率是流速为零时的55%。

壁厚为1 mm，外径分别为20、14和8 mm的两端固支不锈钢燃油管路第1阶固有频率随流速的变化规律如图10所示。在不同外径下，流速对不锈钢管路固有频率影响的相对变化情况如图11所示。

从图10、11中可见，与钛合金管路相同，相同壁厚管路在相同流速下：

（1）随着外径的增大，不锈钢燃油管路的固有频率升高。

（2）随着外径的增大，相对于流速为零时的固有频率变化率减小，这说明流固耦合对于直径小的管路影响更大。例如，在流速为100 m/s时，外径为8 mm的不锈钢管路固有频率是流速为零时的82%。

另外，通过对比可以发现，相同截面特性的不锈钢和钛合金管路，流固耦合对钛合金管路的影响更大。

4 结论

（1）通过Galerkin方法截取适当的模态，可建立1个能反映输液管路流固耦合动力学特性的低阶模型，用于计算其固有振动特性。

（2）航空发动机钛合金燃油管路的实际流动速度远小于其失稳临界流速，因此其不会发生屈曲失稳。

（3）进行航空发动机管路系统振动特性分析时，可忽略哥氏力对不锈钢和钛合金2种管材固有频率的影响，即其阻尼固有频率和无阻尼固有频率相差很小，可以直接使用对称矩阵特征值求解器求其固有振动特性。

（4）相同壁厚的燃油管路，流固耦合对外径小的管路固有频率影响更大；相同截面尺寸的燃油管路，流固耦合对钛合金管路固有频率的影响大于对不锈钢管路固有频率的影响。

[1]Paidoussis M P,Li G X.Pipes conveying fluid:a model dynamical problem[J].Journal of Fluids and Structures,1993,7(2):137-204.

[2]任建亭,姜节胜.输流管道系统振动研究进展 [J].力学进展,2003,33(3):313-324.REN Jianting,JIANG Jiesheng.Advances and trends on vibration of pipes conveying fluid [J].Advances in Mechanics,2003,33(3):313-324.(in Chinese)

[3]Ibrahim R A.Overview of mechanics of pipes conveying fluids—part I:fundamental studies[J].Journal of Pressure Vessel Technology,2010,132(3):034001-034032.

[4]Holmes P J.Pipes supported at both ends cannot flutter[J].Journal of Applied Mechanics,1978,45(3):619-622.

[5]张智勇,沈荣瀛,王强.充液管道系统的模态分析 [J].固体力学学报,2001,22(2):143-149.ZHANG Zhiyong,SHEN Rongying,WANG Qiang.The modal analysis of the liquid-filled pipe system[J].ACTA Mechanica Solida Sinica,2001,22(2):143-149.(in Chinese)

[6]金基铎,宋志勇,杨晓东.两端固定输流管道的稳定性和参数共振[J].振动工程学报,2004,17(2):190-195.JIN Jiduo,SONG Zhiyong,YANG Xiaodong.Stability and parametric resonances of a clamped-clamped pipe conveying fluid[J].Journal of Vibration Engineer,2004,17(2):190-195.(in Chinese)

[7]Tornabene F,Marzani A,Viola E,et al.Critical flow speeds of pipes conveying fluid by the generalized differential quadrature method[J].Journal of Theoretical and Applied Mechanics 2010,3(3):121-138.

[8]杨晓东,金基铎.输流管道流-固耦合振动的固有频率分析 [J].振动与冲击,2008,27(3):80-81.YANG Xiaodong,JIN Jiduo.Comparison of Galerkin method and complex mode method in natural frequency analysis of tube conveying fluid[J].Journal of Vibration and Shock,2008,27(3):80-81.(in Chinese)

[9]齐欢欢,徐鉴.Galerkin模态截断对计算悬臂输液管道固有频率的影响[J].振动与冲击,2011,30(1):148-151.QI Huanhuan,XU jian.Effect of Galerkin modal truction on natural frequency analysis of a cantilevered pipe conveying fluid[J].Journal of Vibration and Shock,2011,30(1):148-151.(in Chinese)

[10]杨超,范士娟.管材参数对输液管流固耦合振动的影响[J].振动与冲击,2011,30(7):210-213.YANG Chao,FAN shijuan.Influence of pipe parameters on fluidstructure coupled vibration of a fluid-conveying pipe[J].Journal of Vibration and Shock,2011,30(7):210-213.(in Chinese)

[11]Lin J Z,Qin L,Zhou E T,et al.Fluid-structure interaction vibration of hydraulic pipe system[J].Advanced Engineering Forum,2011(2):822-827.

[12]Huang Y M,Ge S,Wu W,et al.A direct method of natural frequency analysis on pipeline conveying fluid with both ends supported[J].Nuclear Engineering&Design,2012,253(12):12-22.

[13]Wang L,Gan J,Ni Q.Natural frequency analysis of fluid-conveying pipes in the ADINA system[J].Journal of Physics Conference,2013,448(1):12014-12020(7).

[14]Paidoussis M P.Fluid-structure interactions:slender structures and axial flow[M].London:Academic Press Limited,1998:89-90.

[15]Ewins D J.Modal testing:theory and practice[M].Letchworth:Research Studies Press,1986:156-160.

Analysis for Natural Frequencies of Pipe Conveying Fluid Considering Fluid-Structure Interaction

LI Zhan-ying1，WANG Jian-jun1，QIU Ming-xing2
（1.School of Energy and Power Engineering,Beihang University,Beijing 100191,China;2.AECC Shenyang Engine Research Institute，Shenyang 110015,China）

In order to analyze the effect of Coriolis force and pipe parameters on the natural frequencies,the fluid-structure coupling model of pipe conveying fluid was established using the Galerkin method,and the natural frequencies of the pipe were obtained by the complex-eigenvalue method.Comparing with the experimental data,the analytical results were verified,which indicated that the analytical model is rational.The critical velocity of the test pipe conveying fuel was obtained,and the influence of Coriolis force and the section characteristics to the natural frequencies were investigated.It is found that the fuel velocity of the test pipe is far below the critical velocity.The Coriolis force has little effect on the natural frequencies of both the stainless steel and the titanium alloy pipe.For the pipe in the same thickness,the fluid-structure interaction has much effect on the natural frequency as the out diameter of the pipe decrease.

pipe conveying fluid;fluid-structure interaction;Galerkin method;natural frequency;Coriolis force；aeroengine

V 233

A

10.13477/j.cnki.aeroengine.2017.01.012

2016-05-18

李占营（1983），男，在读博士研究生，研究方向为航空发动机强度、振动和可靠性；E-mail：lizhanying@buaa.edu.cn。

李占营，王建军，邱明星.航空发动机管路流固耦合振动的固有频率分析[J].航空发动机，2017，43（1）：66-70.LIZhanying，WANGJianjun，QIU Mingxing.Analysisfornaturalfrequenciesofpipeconveyingfluidconsideringfluid-structureinteraction[J].Aeroengine，2017，43（1）：66-70.

（编辑：栗枢）