风扇/增压级动平衡工装最佳支承跨距计算方法

杨法立，史新宇，赵洪丰

（中国航发沈阳发动机研究所,沈阳110015）

风扇/增压级动平衡工装最佳支承跨距计算方法

杨法立，史新宇，赵洪丰

（中国航发沈阳发动机研究所,沈阳110015）

某型航空发动机风扇增压级平衡工装采用悬臂支承结构，其支承跨距是该平衡工装的重要设计参数。针对该平衡工装的结构特点建立了最佳支承跨距的理论分析模型，给出了最佳支承跨距计算的解析表达式，并通过数值计算对最佳支承跨距进行了验证。结果表明：平衡工装最佳支承跨距的解析解与数值解一致，建立的最佳支承跨距计算方法可以为风扇增压级平衡工装的支承跨距的参数设计提供理论指导，提高平衡工装的平衡精度和平衡效果。

风扇/增压级；平衡；支承跨距；航空发动机

0 引言

某型航空发动机风扇增压级转子的平衡工装采用悬臂支承结构，该平衡结构与风扇增压级在发动机上的安装结构保持一致，风扇增压级作为悬臂盘需进行动平衡[1]。风扇增压级的平衡精度要求较高，达到了G1等级，高于燃气轮机对转子平衡等级的要求[2]，因此对平衡工装的平衡精度也有较高的要求。在平衡工装设计过程中，其支承跨距是设计过程中的重要参数，其大小将会影响悬臂端风扇增压级转子的挠度变形，从而影响转子的剩余不平衡量大小和转子的平衡等级。关于转子支承跨距参数的确定问题，在机床电主轴设计中已经进行了一定研究[3-6]，但在以往设计中对于悬臂动平衡工装支承跨距根据经验确定，缺少相应的理论计算方法。

为确定悬臂动平衡工装最佳支承跨距的计算方法，并提高平衡工装的平衡精度和平衡效果，有必要对支承跨距参数的计算方法开展相应研究。本文将提高工装平衡精度问题转化求解悬臂端挠度变形最小问题，通过建立力学模型，分析悬臂端挠度变形与支承跨距之间的关系，得到最佳支承跨距的计算方法，为风扇增压级平衡工装支承跨距的参数设计提供理论依据。

1 最佳支承跨距计算模型

风扇增压级平衡工装结构如图1所示。在风扇增压级转子的重力作用下，平衡轴的悬臂端会沿重力方向发生一定的挠度变形，导致转子的重心相对于旋转轴线发生偏移，影响转子的剩余不平衡量，从而降低了平衡工装的平衡效果。在不考虑零部件加工和装配误差的情况下，该偏移量的大小与平衡转速、转子的质量、平衡轴的截面惯性矩、悬臂端伸长量、2支点轴承的支承刚度及支承跨距等因素有关。在进行建模分析支承跨距与悬臂端挠度变形之间的关系时，将转子的质量、平衡轴的截面惯性矩、悬臂端伸长量、2支点轴承的支承刚度等因素设为定值。同时该型航空发动机风扇增压级平衡工装的平衡转速较低，约为900 r/min，属于低速动平衡[7]，在该转速条件下离心载荷作用对转子悬臂端的变形影响较小，因此也不考虑平衡转速的影响。

通过以上分析，将支承跨距的取值作为影响悬臂端挠度变形的惟一变量，通过建立悬臂端变形量与支承跨距之间的函数关系，分析支承跨距对悬臂端挠度变形的影响规律，从而确定悬臂端挠度变形最小时支承跨距的取值大小，此时的支承跨距即为平衡工装的最佳支承跨距。

悬臂端在风扇增压级重力作用下沿重力方向的挠度变形是平衡轴的弹性变形和支承轴承的弹性变形的组合变形。根据材料力学中组合变形的线性叠加原理[8]，将悬臂端的组合变形分解为2部分：（1）假定支承轴承为刚性支承，轴为弹性体时，在风扇增压级重力下平衡轴悬臂端的下沉位移量；（2）假设轴为刚性体，支承轴承为弹性支承时，在风扇增压级重力下平衡轴悬臂端的下沉位移量。

受力分析及位移变形如图2所示。图中示出了在支承跨距为L时，2种挠度变形的模型分析。其中μs为假设支承轴承为刚性支承、平衡轴为弹性体时，在风扇增压级重力下平衡轴悬臂端的下沉位移量；μb为假设平衡轴为刚性体、支承轴承为弹性支承时，在风扇增压级重力下平衡轴悬臂端的下沉位移量。风扇增压级在悬臂端总的挠度变形μ是μs和μb的线性叠加，因此μ的表达式为

μ=μs+μb（1）

对于平衡轴为弹性体状态下的悬臂端变形μs的求解，可参考材料力学和机械设计手册中的外伸梁的挠度计算公式

式中:F为风扇增压级重力；N、E为平衡轴材料的弹性模量，N/m2；I为平衡轴的截面惯性矩，m4；a 为悬臂端外伸长度，m。

对支承为弹性状态下的悬臂端变形μb的计算如下：从图2中可知平衡轴2支点所受的支反力分别为F1和F2；2支点的支承刚度分别为K1和K2，则在该支反力的条件下2支点的位移量分别为可根据力和力矩平衡关系得到2支反力的表达式

在该状态下平衡轴为刚性体，根据图中的几何关系，可以得到μb的表达式

因此考虑平衡轴弹性变形和支承弹性变形条件下，风扇增压级端总的位移量的表达式为

在悬臂端的外伸长度、平衡轴截面惯性矩、轴承的型号和载荷参数全部确定的条件下，通过总挠度变形μb的表达式可知，总位移μs是关于跨距L的函数。因此，求解平衡轴最佳支承跨距的问题，就是确定悬臂端挠度变形最小时的支承跨距的取值的问题，并且支承最佳跨距一定存在。根据极值定理可知μ取最小值的条件为因此对总位移表达式μ进行求导，通过整理可得

根据卡尔丹求根公式可以证明该3次方程有且只有1个正实根[9]，其表达式为

在已知支承刚度和悬臂端长度的条件下，根据式（8）得到悬臂平衡工装的最佳支承跨距的理论解Lop。悬臂平衡工装的支承跨距取该值条件下，悬臂端的静挠度变形最小，平衡工装的平衡精度最高。

2 最佳支承跨距计算

2.1 模型参数确定

根据上述分析可知，若确定平衡工装的支承跨距，首先需要确定模型参数，包括平衡轴截面惯性矩I，2支点支承刚度K1、K2，悬臂端伸长量a和悬臂端承受载荷F。

为保证悬臂端的静挠度最小，并考虑到风扇增压级的具体结构尺寸的限制，a值应取结构所允许的最小值，对于该型号a=260 mm。在轴承型号确定的情况下，平衡轴的截面惯性矩基本保持不变，对于本型号的平衡工装，其平衡轴的截面惯性矩约为6.76e-6 m4。该型航空发动机的风扇增压级的动平衡不带风扇大叶片，其悬臂端所受的载荷力仅为风扇增压级及其相应工装夹具的质量，其载荷力约为1.764 kN平衡工装的支点1采用成对安装的单列圆锥滚子轴承，支点2采用双列圆柱滚子轴承。圆锥滚子轴承和圆柱滚子轴承的径向刚度的近似计算公式[10]为

式中：Krr为径向刚度，N/mm；B为滚子有效长度，mm；n为滚子数目；β为接触角；Fr为径向力，N。

根据发动机风扇增压级转子和平衡机支承摆架的尺寸限制，支承跨距L的范围为300～3300 mm。在不考虑工装及平衡轴的重力作用对轴承的载荷影响，根据支反力计算公式（3）和轴承刚度计算公式（9）,并将轴承的几何参数及所受径向力带入，得到2个支点的单个轴承的支承刚度范围和刚度，见表1。其中总刚度Kavg是单个轴承的支承刚度范围平均值的2倍。

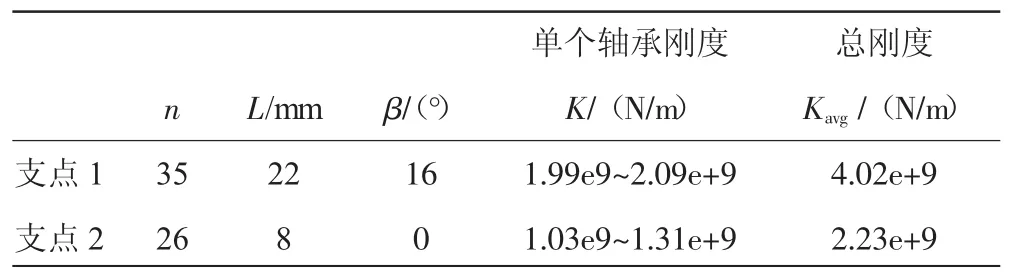
表1 支点支承刚度计算值

由于该工装支点1的轴承座为悬臂支承的圆筒，因此在对支点2的支承刚度进行计算时，还应考虑该支点轴承刚度与弹性轴承座刚度之间的串联关系。相关研究表明：应用有限元方法来计算支承部件的支承刚度是1种有效方法，其精度远远高于传统的近似解法[11-12]。因此通过对支点1悬臂支承座进行有限元仿真计算，得到其支承刚度约为1.9e+8 N/m，其仿真计算位移如图3所示，支承跨距模型的优化计算参数见表2。其中支点1的刚度为串联后支点1的总支承刚度。

表2 支承跨距优化计算参数

2.2 最佳支承跨距计算结果

根据模型分析过程可知，最佳支承跨距计算表达式（8）是在支承刚度为定值的条件下确定的。但根据支承刚度计算公式（9）和支反力公式（3）表明，2个支点支承刚度是关于跨距的函数，因此在应用式（8）进行求解最佳支承跨距时，需要将2个支点的支承刚度设为定值。此处将2个支点支承刚度的平均值作为计算参数，因此将表2中参数带入到式（8）中，可得最佳支承跨距L=0.52 m。

根据悬臂端总挠度变形计算公式（5）可知，在该表达式中支承刚度同样是关于支承跨距L的函数，因此将支承刚度公式（9）和支反力公式（3）带入总挠度变形公式（5）中，可得总挠度变形关于支承跨距的函数表达式

在支承跨距L取值范围300～3300 mm内，对联立后的悬臂端总挠度变形公式（10）进行数值计算，可得挠度变形随支承跨距的变化关系，如图4所示。从图4（a）中可见，跨距从0.3 m增加到3.3 m时，挠度变形先减小，然后不断增大，在0.52 m处挠度变形最小，因此通过数值计算方法得到的最佳支承跨距为0.52 m，与解析表达式的计算结果一致。

3 结论

（1）针对某型航空发动机风扇增压级平衡工装的最佳支承跨距的参数设计问题进行研究，通过对分析模型求解，得到了最佳支承跨距计算的解析表达式。通过带入平衡工装的结构参数，得到了该型号风扇增压级平衡工装的最佳支承跨距，并且通过与数值计算结果对比，验证了最佳支承跨距计算解析表达式的正确性。

（2）确定的最佳支承跨距计算方法可用于指导悬臂类航空发动机风扇增压级平衡工装最佳支承跨距的参数设计，在该支承跨距的参数条件下可以保证平衡工装悬臂端的变形最小，从而提高工装的平衡效果和平衡精度。

（3）所建立的最佳支承跨距的计算方法没有考虑振动测试面与不平衡量校正面之间平面分离误差及支点允许支反力载荷的影响，因此在应用本文给出的最佳支承跨距的计算方法时，还应参考平衡设备的具体参数。

[1]付才高.转子动力学及整机振动[M].北京:航空工业出版社,2000：401-403.FU Caigao.Rotor dynamics and whole engine vibration[M].Beijing:Aviation Industry Press,2000：401-403.（in Chinese）

[2]全国机械振动与冲击标准化技术委员会.GB/T 9239.1-2006机械振动恒态（刚性）转子平衡品质要求第一部分:规范与平衡允差的检验[S].北京:中国标准出版社,2007：6-8.National Technical Committee on Mechanical Vibrations and Impacts of Standardization Administration of China.GB/T 9239.1-2006 Mechanical vibration-balance quality requirements for rotors in a constant（rigid）-part1:specification and verification of balance tolerances[S].Beijing:International Organization for Standardization,2007：6-8.（in Chinese）

[3]张济生.主轴部件最佳支承跨距的精确计算 [J].制造技术与机床,1996（4）:36-37.ZHANG Jisheng.The accurate calculation of spindle bearing span[J].Manufacturing Technology and Machine Tool,1996 （4）:36-37.（in Chinese）

[4]张国通.高速陶瓷电主轴设计及动静态性能分析[D].秦皇岛:燕山大学,机械工程学院,2015.ZHANG Guotong.Design and high-speed ceramic motorized spindle static and dynamic performance analysis[D].Qinhuangdao:Yanshan University,Machinery Manufacturing Academic.（in Chinese）

[5]裴大明,冯平法,郁鼎文.基于有限元方法的主轴轴承跨距优化[J].机械设计与制造,2005（10）:44-46.PEI Daming,FENG Pingfa,YU Dingwen.Optimum design of spindle bearing distance based on FEM[J].Machinery Design&Manufacture,2005（10）:44-46.（in Chinese）

[6]李松生,杨柳欣,王兵华.高速电主轴轴系转子动力学特性分析[J].轴承，2002（2）:15-17.LI Songsheng,YANG Liuxin,WANG Binghua.Dynamics characteristic analysis of high speed electric spindle shaft rotors[J].Bearing，2002（2）:15-17.（in Chinese）

[7]陈炳贻.航空发动机平衡工艺技术[J].航空科学技术,1996（2）:7-10.CHEN Bingyi.Balance technology of aircraft engine[J].Aeronautical Science and Technology,1996（2）:7-10.（in Chinese）

[8]苟文选.材料力学[M].北京:科学出版社，2005：40-42.GOU Wenxuan.Material mechanics[M].Beijing:Science Press,2005：40-42.（in Chinese）

[9]数学手册编写组.数学手册[M].北京:人民教育出版社,1979：88-89.Mathematics Handbook Compilation Group.Mathematics handbook[M].Beijing:People’s Education Press.1979：88-89.（in Chinese）

[10]陈忠.滚动轴承及其支承的刚度计算 [J].煤矿机械,2006（3）:387-388.CHEN Zhong.Stiffness computation of rolling bearing and its support[J].Coal Mine Machinery,2006（3）:387-388.（in Chinese）

[11]龙向阳,洪杰,张大义,等.弹性环刚度强度的分析方法与力学特性研究[J].热能动力工程,2010,25（2）:145-149.LONG Xiangyang,HONG Jie,ZHANG Dayi,et al.Study of the methods for analyzing the rigidity and strength of an elastic ring and its mechanics characteristics[J].Journal of Engineering for Thermal Energy and Power,2010,25（2）:145-149.（in Chinese）

[12]程小勇,陈果,李成刚,等.航空发动机转子系统模拟支承设计与刚度计算[J].航空计算技术,2012（6）:9-12.CHENG Xiaoyong,CHEN Guo,LI Chenggang,et al.Rotor support simulation design and equivalent stiffness computation for aeroengine[J].Aeronautical Computing Technique,2012（6）:9-12.（in Chinese）

Calculation Method of Optimum Bearing Span of Fan/Booster Balancing Tool

YANG Fa-li,SHI Xin-yu,ZHAO Hong-feng
（AECC Shenyang Engine Research Institute,Shenyang 110015,China）

The cantilever structure is adopted in balance tool of an aeroengine fan/booster,and the balance tool bearing span is an important design parameter.The theoretical analysis model of the optimal bearing span was established according to the structure characteristics of the balance tool,and the analytical expression of the optimal bearing span was obtained.The result of expression was validated by numerical simulation.The results show that the theoretical result of the optimal bearing span is consistent with numerical calculation,and the calculation method of optimal bearing span can provide guidance to the parameter design of bearing span for balance tool of fan/booster,which can improve the balance accuracy and quality of balance tool.

fan/booster;balance;bearing span;aeroengine

V 241.05

A

10.13477/j.cnki.aeroengine.2017.01.006

2016-06-30 基金项目：国家重大基础研究项目资助

杨法立（1986），男，硕士，工程师，主要从事航空发动机装配及高低压转子平衡的研究工作；E-mail:faliyang@163.com。

杨法立，史新宇，赵洪丰.风扇/增压级动平衡工装最佳支承跨距分析计算[J].航空发动机，2017，43（1）：27-31.YANGFali,SHI Xinyu,ZHAO Hongfeng.Calculationmethodofoptimumbearingspanoffan/boosterbalancingtool[J].Aeroengine，2017，43（1）：27-31.

(编辑：张宝玲)