公路桥梁抗震设计方法及实例分析

翟晓春

（山西省交通科学研究院，山西 太原030006）

近年来，随着我国交通体系现代化的不断提高，大量公路桥梁得以新建，人们交通出行变得更加高效、便捷。然而，我国幅员辽阔，地震带分布较广，不同震级的地震频繁发生，地震带来的自然灾害对人们生产生活造成较大影响，也在一定程度上威胁公路桥梁的安全使用[1]。在2008年汶川特大地震中，众多桥梁遭受到不同程度的震害影响，而采用合理抗震设计的公路桥梁受损较小，成为震后救灾的重要生命通道，为及时抢救受灾群众、运送应急物资创造了宝贵机会，由此可见抗震设计对于地处地震频发区的桥梁具有重要的意义[2]。良好的抗震设计对提高桥梁的抗震性能具有关键作用，在遭遇震害时亦能减少损失。因此，进行公路桥梁的抗震设计，应当严格遵循设计规范、标准及其他要求，结合既有工程经验，符合以下几点设计要点：提高体系整体性、强化体系刚度和延性、采用强度差异性设计理念、设置多道防线、实行多水准设防[3]。桥梁抗震设计常用方法主要是以强度为核心的设计方法、考虑结构延性的设计方法、以结构性能为目标的设计方法[4]。本文基于某公路连续刚构桥进行了抗震计算分析，阐述了公路桥梁抗震设计方法的应用过程，可为类似公路桥梁抗震设计提供参考。

1 数值计算分析

1.1 有限元模型

某桥桥跨布置为（30+50+30）m变截面悬浇预应力混凝土连续刚构+2×20 m钢筋混凝土等截面连续箱梁，全桥长167.08 m，宽12 m。设计荷载等级为公路-Ⅰ级。

本文采用大型通用有限元程序MIDAS Civil进行有限元模拟。模型边界条件为：主梁和主墩处固结约束，主梁与交界墩处竖、横向约束，纵向活动，有限元离散模型如图1所示，其中纵桥向为x方向，横桥向为y方向，竖向为z方向，左侧墩为1号，右侧墩为 号

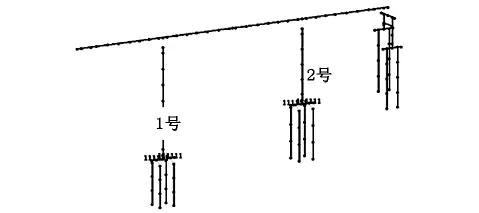
图1 有限元模型示意图

1.2 结构自振特性分析

合理的地震响应分析，是建立在准确的动力特性基础上的。为此，首先需要进行特征值分析，数值计算得到结构前10阶频率及相应的振型，如表1所示。

表1 大桥前10阶频率及振型

部分振型如图2所示。

图2 部分模态振型图

1.3 地震响应分析

根据《公路桥梁抗震设计细则》，对A类桥梁的抗震设防目标是中震（E1地震作用，重现期约为475年）不坏，大震（E2地震作用，重现期约为2 000年）可修。在本桥地震响应分析中，采用“二水准”的研究方法，即中震作用下结构必须满足强度的要求，大震也即罕遇地震作用下验算结构的位移或变形能力。在本桥施工图设计阶段，按照规范要求的“二水准”研究方法，验算内容包括以下两个内容[5-7]：

a）E1地震作用（中震，常遇地震，50年5%的超越概率）下验算结构的强度。

b）E2地震作用（大震，罕遇地震，50年1%的超越概率）下验算结构的强度及位移。

反应谱分析中考虑对横桥向、竖桥向和顺桥向激励的地震波进行分析。

根据地勘资料可知，桥址区场地类别为Ⅰ类，地震动反映普特征周期0.40 s，地震动峰值加速度为0.20g，相应地震基本烈度为8（Ⅷ）度。地震输入采用两种方式：纵向＋竖向；横向＋竖向，并取前200阶（振型参与质量达99%），按CQC法进行组合，阻尼比为0.05。场地地震基本烈度Ⅷ度，设计加速度反应谱及地震影响系数如下。

抗震分析采用多振型反应谱法，水平设计加速度反应谱S由式（1）确定：

式中：Tg为特征周期，s；T 为结构自振周期，s；Smax为水平设计加速度反应谱最大值；Ci为抗震重要性系数；Cs为场地系数；Cd为阻尼调整系数；A为水平向设计基本地震加速度峰值。

反应谱拟合的相关参数见表2。

表2 反应谱拟合相关参数表

竖向加速度反应谱按照《公路桥梁抗震设计细则》5.2.5条，竖向设计加速度反应谱由水平向设计加速度反应谱乘以竖向/水平向谱比函数R，考虑工程场地条件，取值按照基岩场地，R=0.65。根据以上参数计算的E1、E2地震影响系数曲线如图3、图4所示。

图3 E1地震影响系数曲线

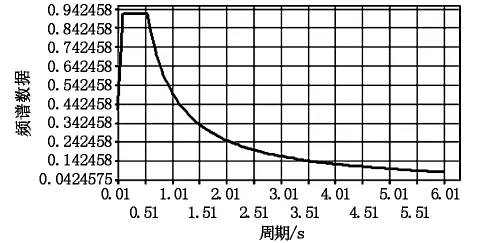
图4 E2地震影响系数曲线

反应谱分析中，按照表3方式进行荷载组合。

表3 荷载组合表

受篇幅所限，以下仅给出部分主梁应力及桥墩弯矩计算结果如图5～图7所示。

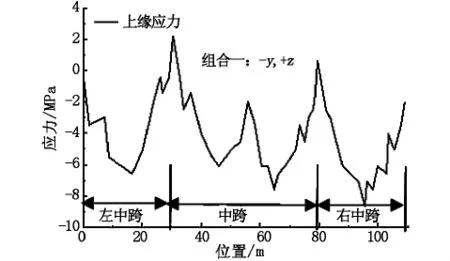
图5 组合一作用主梁上缘应力图

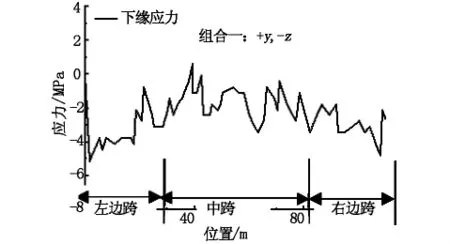
图6 组合一作用主梁下缘应力图

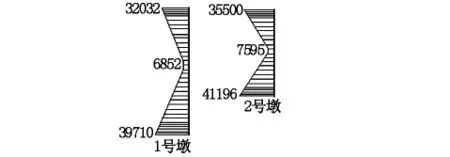
图7 组合一作用桥墩最不利弯矩（单位：kN·m）

由图5～图7可知，E1作用下最大弯矩在墩底和墩顶处，最大弯矩为4.11×104kN·m，通过计算该处桥墩的抗弯承载力为7.90×104kN·m，承载力满足要求。

E2地震作用下各墩弯矩计算结果如图8所示。

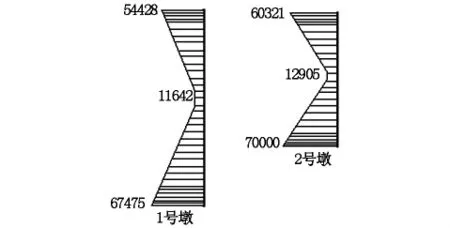
图8 组合四作用下桥墩最不利弯矩（单位：kN·m）

由图8可知，E2作用下最大弯矩为7.0×104kN·m，通过计算该处桥墩的抗弯承载力为1.35×105kN·m，承载力满足要求。

E2地震作用下，主梁纵向位移图如图9所示。

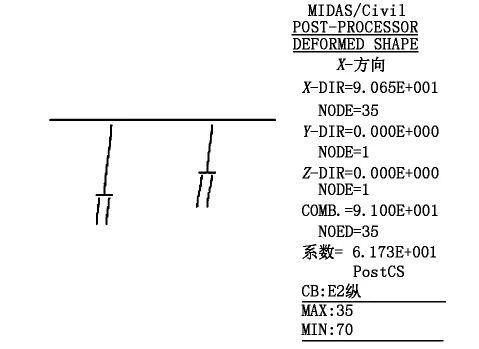
图9 E2地震作用下主梁纵向位移（单位：mm）

由图9可知，主梁纵向最大位移为9.1 cm，主桥边跨梁端采用的是80型伸缩缝，最大伸缩量为±4 cm，则伸缩缝不能满足E2地震作用下结构对位移的要求。

综上所述，在E1地震作用下，全桥处于弹性阶段，主梁最大拉应力均没有超过混凝土的抗拉强度标准值。在E2地震作用下，较矮的2号墩拉应力较大，但其工作状态仍然是弹性阶段，其承载力满足要求。在E2地震作用下，主梁伸缩缝间距略小于桥梁位移。

2 结语

本文基于某连续刚构桥进行了两阶段抗震设计，对E1地震作用下，进行了强度验算，E2地震作用下进行了强度及位移验算。主要得到以下结论：

a）在E1地震作用下，全桥处于弹性阶段，主梁最大主拉应力均没有超过混凝土的抗拉强度标注值。

b）在E2地震作用下，较矮的墩受力更为不利，但其仍然处于弹性工作状态，表明对于该类桥矮墩受力需要更为重视。

c）在E2地震作用下，主梁伸缩缝最大伸缩量略小于桥梁的位移，表明设计选用的边跨80型伸缩缝不能满足E2地震抗震需求，需要进一步优化伸缩缝选型。