成型炸药滑动摩擦系数的测试与修正
2017-11-09罗毅刘彦黄风雷
罗毅, 刘彦, 黄风雷
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
成型炸药滑动摩擦系数的测试与修正
罗毅, 刘彦, 黄风雷
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
为研究动摩擦系数对于成型炸药摩擦点火的影响,利用自行设计的基于落锤的摩擦测试系统,以8701压装成型炸药为研究对象,研究了不同压力环境下成型炸药与45号钢之间的动摩擦系数。试验结果表明,当界面压力由1 MPa升高到10 MPa时,动摩擦系数将由0.28降低至0.10,说明动摩擦系数具有压力相关性。基于试验结果,提出了该炸药的摩擦系数计算模型。通过LS-DYNA二次开发,添加了试验所得摩擦系数计算模型,对8701炸药滑道试验进行了摩擦点火热力化耦合数值模拟。计算结果表明,修正的摩擦系数计算模型会延长炸药点火延迟时间,提高临界点火速度和临界点火温度,也说明考虑了压力相关性的摩擦系数计算模型对于研究成型炸药的摩擦点火问题有重要意义。
兵器科学与技术; 成型炸药; 摩擦系数; 摩擦点火; 落锤冲击
0 引言
在勤务处理过程中,成型炸药由于意外跌落可能会发生斜撞击摩擦,引发炸药局部发生点火反应。针对上述问题,滑道试验是鉴定炸药作业安全最有效的方法[1-4]。斜撞击过程中,炸药件局部发生塑性变形,并与滑道发生剧烈摩擦,从而在短时间内将机械能转化为热能并形成热点。撞击过程中,摩擦生热对炸药温升具有重要作用[5-7]。通常,炸药与滑道之间摩擦系数的确定主要参照国家标准GB10006—1988塑料薄膜和薄片摩擦系数测定方法。摩擦系数测定时,所用滑块底面积为40 cm2,总质量为200 g,界面正压力接近500 Pa. 但是,众多研究表明[8-10],界面正压力的增加会导致滑动摩擦系数减小,从而影响摩擦生热的过程。因此,国家标准测定方法所得摩擦系数难以反映高压下炸药与外界的摩擦系数,影响滑道试验摩擦生热计算的准确性。定量分析成型炸药摩擦系数与界面正压力的关系,能够更好地指导滑道试验摩擦点火的理论计算和数值模拟。基于传统的炸药摩擦感度试验[11-12],国内外研究者设计了一系列定量分析试验[13-16]。但是目前的试验手段不能保证,在高压高速加载条件下,成型炸药块体的完整性。当界面正压力达到比较高的水平时,成型炸药容易发生剪切断裂、破碎,难以完整反映压力对于摩擦系数的影响。
本文针对高压下炸药装药与45号钢壳体摩擦的条件,自行设计了基于落锤的摩擦测试系统。在保证8701成型炸药不破碎的情况下,对8701炸药与45号钢之间的摩擦系数进行了试验研究,分析了摩擦系数与界面正压力的相关性,并得到了二者之间的拟合曲线。然后基于Sun等[17]摩擦点火数值模拟工作,本文对LS-DYNA进行了二次开发并修改了摩擦系数计算模型,引入了界面正压力对于滑动摩擦系数的影响,对滑道试验中8701炸药摩擦点火问题进行了数值模拟,分析了修正模型对8701炸药温升速率、临界点火温度和临界点火速度的影响。
1 摩擦试验过程与结果
摩擦测试系统如图1所示,由落锤加速系统和摩擦系数测试系统两部分组成。试验前,通过标定位置保证两套系统同轴匹配,且不影响落锤和下方系统作用过程。为了尽可能消除落锤发射时振动对后期摩擦力信号的影响,两套系统进行了物理隔离。试验时,首先通过装置底部液压缸体向核心模块中炸药药片施加轴向应力pa,进而使炸药产生径向膨胀挤压摩擦套筒,通过贴于套筒外侧的周向应变片,测得套筒外壁的周向应变εt,装药结构如图2所示。

图1 摩擦测试系统Fig.1 Friction test system
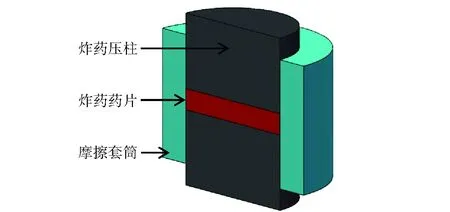
图2 预加压核心模块Fig.2 Prepressured kernel module
加压过程中套筒始终保持弹性,因此可以从周向应变εt推导出套筒内壁与炸药药片之间的正压力pn,即
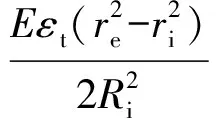
(1)
式中:E是套筒材料的弹性模量;re是外部半径;ri是内部半径。本次试验所用45号钢套筒弹性模量为290 GPa,外部直径为45 mm,内部直径为30 mm,内壁表面粗糙度Ra为0.4 μm.
炸药药片加压完毕后,向装置上方气缸内充入空气,剪断落锤侧方销钉(销钉采用45号钢制成),释放落锤并在气缸内加速下滑,最后撞击下端的摩擦套筒,使摩擦套筒与炸药药片之间产生摩擦。本次试验所用销钉直径为3 mm,落锤撞击速度为10 m/s. 此外,为了防止短时间冲击所产生噪声对摩擦力信号的影响,摩擦套筒上方还粘贴了厚度为1 cm的橡胶垫,延长撞击作用时间,提高信噪比。
套筒与炸药之间的摩擦开始后,药片下方的轴向压力传感器可以测量不同界面正压力下轴向力的增量,即为摩擦力f的大小。通过套筒内壁的正压力pn乘以炸药的侧面积,可得摩擦时的界面正压力Fn,进而根据μ=f/Fn得到炸药药片与金属套筒之间摩擦系数μ为

(2)
式中:L为炸药药片的厚度。试验所用药片直径为30 mm,厚度为5 mm,如图3所示。由于三向围压的作用,炸药在高压高速摩擦过程中能够较好地保持完整性,不会发生断裂、破碎的情况。因此本试验装置可以保证所测数据能够真实地反映成型炸药与45号钢之间高压高速条件下的摩擦系数响应情况。
不同正压力情况下,炸药药片下方轴向压力传感器所获的轴向摩擦力大小如图4所示。当落锤刚撞击到摩擦套筒时,在静摩擦力的作用下,套筒将会保持静止;当作用力超过最大静摩擦力时,套筒开始运动。摩擦力信号的第1个峰值即为最大静摩擦力。随后,套筒开始滑动,后续波形基于一定水平出现持续震荡,主要因为炸药与套筒摩擦时,迟滞作用导致弹性势能的阶段性释放,形成了黏滑现象。震荡阶段摩擦力的平均值,即为对应压力下炸药药片与45号钢套筒之间的滑动摩擦力f. 此外,由套筒内壁正压力pn可得套筒内壁径向力Fn,进而可得滑动摩擦系数μ. 试验结果如表1所示。
表1数据表明,随着界面正压力的增大,在相同输入冲量下,8701成型炸药与45号钢的摩擦系数随着界面正压力的升高而逐步降低。当套筒内壁正压力超过10 MPa后,摩擦系数基本趋于稳定,维持在0.1附近。试验结果表明,本摩擦测试系统能够在保持成型炸药完整性的前提下,实现成型炸药的摩擦系数压力响应特性分析。
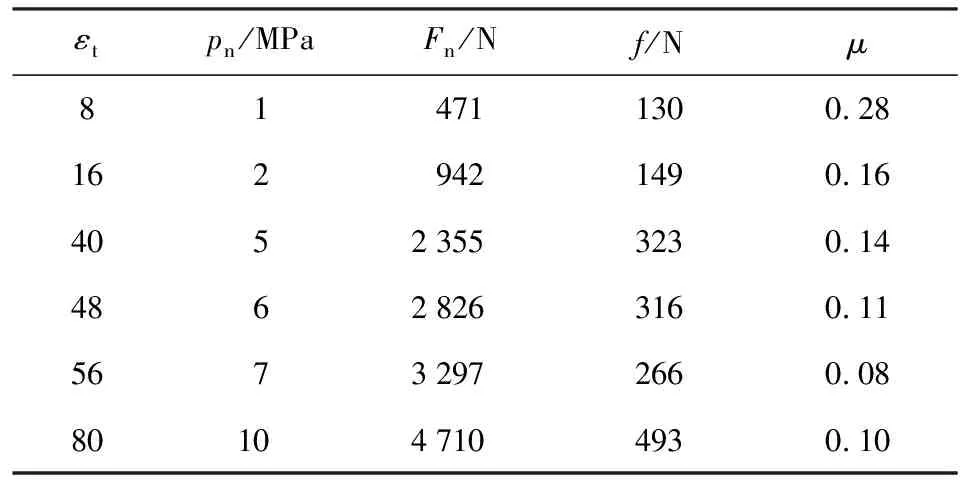
表1 摩擦系数与套筒内壁径向压力之间的关系
2 LS-DYNA摩擦系数计算模型修正
LS-DYNA作为一款在兵器科学研究领域应用广泛的动力分析软件[18-21],其优异的界面接触处理能力一直广受使用者的好评。因此,采用该软件进行数值模拟可以分析炸药的摩擦生热问题[17, 22]。LS-DYNA中摩擦力的计算基于经典库仑摩擦定律,即滑动摩擦力等于摩擦系数乘以界面正压力。其中,摩擦系数μ由动摩擦系数μd和静摩擦系数μs共同控制,并通过一个指数函数来实现动、静摩擦系数之间的平稳过渡,且随着摩擦速度v的增加,摩擦系数还会在衰减常数τ的控制下逐渐减小,即
μ=μd+(μs-μd)exp(-τv).
(3)
8701炸药摩擦试验结果显示,随着界面正压力的升高,摩擦系数在一定压力范围,随着正压力的增大而降低,当正压力增加到10 MPa之后,8701炸药与45号钢的摩擦系数约为1 MPa时的40%. 如果摩擦生热计算中依然采用低压情况下的摩擦系数,将会导致摩擦生热的计算值产生较大误差,与试验结果不符。然而,LS-DYNA中并未考虑摩擦系数的压力相关性。对于变正压力摩擦问题,如炸药块体滑道试验、跌落分析等,摩擦界面正压力在分析过程中不断发生变化,LS-DYNA数值模拟中无法根据压力变化实时调整摩擦系数的大小,从而无法反映该炸药摩擦生热的真实过程。
因此,为了更准确地分析炸药摩擦过程中热力耦合关系,能够根据试验结果实时调整摩擦系数与压力之间的关系,需要修正LS-DYNA原有的摩擦系数计算模型。
通过对8701成型炸药试验结果的分析,炸药与45号钢之间动摩擦系数随着压力的变化大致分为两个阶段:第1阶段,当压力处于1~10 MPa之间时,炸药与45号钢之间动摩擦系数随着压力增大不断减小,且变化率不断降低,直至摩擦系数趋于稳定;第2阶段,当压力高于10 MPa时,炸药与45号钢之间动摩擦系数不再发生改变,维持在0.1附近。针对上述摩擦系数变化的特点,通过试验数据拟合分析表明,摩擦系数前期变化过程满足指数衰减规律。因此,新模型中摩擦系数的计算为
(4)
式中:m、n和q是3个可调整的参数,其中m表示高压情况下炸药摩擦系数的稳定值,约为低压(1 MPa)摩擦系数的40%,如上述试验中高压状态下8701炸药摩擦系数稳定值为0.1,n表示低压(1 MPa)和高压稳定状态下摩擦系数的差值,q表示与炸药剪切强度相关的一个经验常量(MPa);pc是临界压强,超过临界压强摩擦系数恒定不变。
该模型能够保证摩擦系数在整个计算过程中的平稳过渡,同时还能反映压力与摩擦系数相关性。为了验证压力变化对摩擦系数,以及新模型对于摩擦力热耦合计算的影响,本文通过对LS-DYNA二次开发,成功引入新的摩擦系数计算模型,得到了对应的求解器,并对8701炸药在滑道试验中的响应情况进行了数值模拟,对比了修正前后模型对于点火过程的影响。
3 滑道试验数值模拟
利用上述改进的摩擦系数计算模型,能够解决变压力情况下的摩擦问题。此外,炸药与滑道撞击的过程中,由于接触面积小、压力大,炸药会发生一定程度的塑性变形,塑性功所转化的热量对炸药局部温升也有较大贡献。综合上述特点,本文将含热分解放热反应的热弹塑性材料模型和修正的摩擦系数计算模型相结合,并对炸药采用任意的拉格朗日- 欧拉算法,对滑道采用拉格朗日算法,对8701炸药滑道试验摩擦点火问题进行了分析。
由于摩擦时主要是炸药柱体下方局部区域与滑道发生摩擦,为了简化模型,本文不考虑国家军用标准滑道试验中的盖板、托环和半球基体等部件,而是将整体试件质量全部赋予炸药,并建立了如图5所示的炸药半球模型。炸药半球半径为13 cm,密度为1.7 g/cm3,滑道长40 cm,宽20 cm. 撞击初速度直接加载在炸药半球上,不再依靠重力势能的转化获得。

图5 滑道试验计算模型Fig.5 Calculation model of skid test
炸药药片采用各向同性热传导模型和带化学反应的热弹塑性本构模型,主要考虑界面摩擦生成热和塑性功转化热对温升的贡献。炸药密度为1.72×103kg/m3,导热率为0.302 W/(m·K),比热容为971 J/(kg·K). 炸药热分解放热反应由Arrhenius方程控制,指前因子为2.02×1018s-1,活化能为1.97×105J/mol,分解反应热为2.09×106J/kg. 温度为298 K时,炸药弹性模量为5 GPa,泊松比为0.26,线膨胀系数为1.924×10-4K-1;温度为398 K时,炸药弹性模量为1.32 GPa,泊松比为0.262,线膨胀系数为2.29×10-4K-1[23].
滑道也采用各向同性热传导模型,并将其视为刚体。根据国家军用标准GJB 772A—97炸药试验方法,真实滑道试验中会在45号钢滑道表面喷涂1.0~1.3 mm厚的石英砂,并用环氧树脂粘结,因此滑道密度设为7.9×103kg/m3,弹性模量为211 GPa,泊松比为0.3,比热容为1 012 J/(kg·K),热导率为0.2 W/(m·K)。
4 数值模拟结果
设炸药初始撞击速度与水平方向夹角为14°,环境初始温度为298 K. 当不考虑压力对摩擦系数的影响时,炸药与滑道的摩擦系数采用国标方法进行标定。参考申春迎等[7]工作,低压情况下(正压力为500 Pa)炸药与滑道之间摩擦系数为0.5,且不随压力的变化而发生变化。当考虑压力对摩擦系数的影响时,采用带有新计算模型的求解器分析炸药摩擦过程。新模型参数设置为:m=0.2,n=0.3,q=3 MPa. 在不同撞击速度条件下,分析了8701炸药滑道试验的温升过程。摩擦过程中,炸药与滑道接触面积较小,温升区域位于半球顶部。此外由于摩擦过程中重心前移,因此对称轴前方节点温升速率最大,温升过程如图6所示。
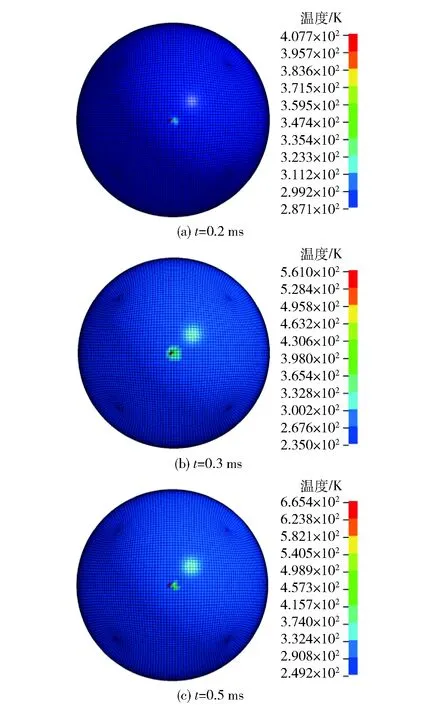
图6 炸药底部温升过程(v=11 m/s,μ=0.5)Fig.6 Temperature rising process at the bottom of explosive (v=11 m/s,μ=0.5)
分别采用LS-DYNA自带的摩擦系数计算模型和修正模型对8701炸药滑道试验进行分析,炸药温升过程如图7所示。当采用原模型时,撞击速度为11 m/s、9 m/s、7 m/s时,温升曲线末端都出现了拐点,说明炸药发生了点火反应。点火时间tc随着加载速度的减小而逐渐延长,且点火温度Tc随着加载速度的减小略有上升:v=11 m/s时,tc=0.50 ms,Tc=665 K;v=9 m/s时,tc=0.69 ms,Tc=667 K;v=7 m/s时,tc=0.98 ms,Tc=677 K. 当撞击速度为5 m/s时,温升曲线没有拐点出现,炸药不发生点火反应,说明使用原模型时,8701炸药在此种工况的临界点火速度位于5~7 m/s之间。

图7 8701炸药滑道试验温升计算结果Fig.7 Temperature rising processes at different impact velocities
当采用修正模型时,相同加载速度下,炸药点火时间延长且临界点火温度提高。v=11 m/s时,tc=0.74 ms,Tc=673 K;v=9 m/s时,tc=1.05 ms,Tc=675 K. 炸药临界点火速度位于7~9 m/s之间,比原模型计算所得的临界点火速度有所提高。
两种模型结果的差异主要由于摩擦过程中界面压力的变化,导致修正模型中摩擦系数偏低,从而延长点火时间并提高临界点火速度。当v=11 m/s,采用修正模型时,炸药顶部单元压力变化如图8所示。从图8中可以看出,摩擦过程中压力水平较高,大多数时候维持在10 MPa以上。

图8 炸药底部正压力时间历程曲线(v=11 m/s)Fig.8 Normal pressure-time history at the bottom of explosive (v=11 m/s)
5 结论
针对传统试验方法无法反映动摩擦系数对于炸药摩擦点火影响的问题,设计了基于落锤的摩擦测试系统,以8701压装成型炸药为例,研究了不同压力环境下成型炸药与45号钢之间的动摩擦系数。基于试验结果,建立了该炸药的修正摩擦系数计算模型,并分析了动摩擦系数对于炸药点火时间与点火温度的影响。主要结论有:
1) 设计的摩擦测试系统能够保证摩擦过程中成型炸药的完整性,并能够有效分析成型炸药与外界摩擦系数响应规律。试验结果表明,外界压力对于8701炸药的摩擦系数有重要影响,且随着压力的升高,摩擦系数会下降60%,并在高压阶段维持一定水平。将摩擦系数分为低压(1~10 MPa)与高压(>10 MPa)两个阶段分别计算,通过摩擦系数与界面正压力的曲线拟合,得到了计算二者相关性的公式。
2) 引入界面正压力与动摩擦系数的相关性,建立了修正的摩擦系数计算模型。对撞击过程中8701成型炸药的摩擦点火过程进行滑道试验数值模拟,研究表明,修正前后摩擦系数计算模型得到的结果有着明显差异。与未修正动摩擦系数的计算模型相比,修正模型计算出的炸药点火时间有所延长,且临界点火速度有所提高。
综上所述,动摩擦系数确实对炸药的摩擦点火有显著影响。结合本套摩擦系数测试系统,还能对其他成型炸药的摩擦系数进行分析,从而建立相应的计算模型,有助于改进对炸药安定性的准确评估。此外,除界面正压力外,界面的非均匀性、温度的变化、炸药物质组成状态等因素都会对炸药摩擦系数的变化有所影响,因此,后期工作中还需继续分析其他因素对摩擦系数的影响,进一步完善炸药摩擦点火过程的研究。
References)
[1] Asay B. Shock wave science and technology reference library [M]. Berlin, Germany: Springer, 2008:293-617.
[2] Heatwole E, Parker G, Holmes M, et al. Grit-mediated frictional ignition of a polymer-bonded explosive during oblique impacts: probability calculations for safety engineering[J]. Reliability Engineering and System Safety, 2015, 134:10-18.
[3] White B W, Springer H K, Reaugh J E. Computational studies of the skid test: evaluation of the non-shock ignition of LX-10 using HERMES[J]. Journal of Physics: Conference Series, 2014, 500(19):192021.
[4] Dickson P, Parker G, Novak A, et al. Frictionally induced ignition processes in drop and skid tests, LA-UR-10-2186 [R]. Los Alamos, NM, US: Los Alamos National Laboratory, 2010.
[5] 林文洲, 洪滔. 高能炸药摩擦感度的数值模拟[J]. 爆炸与冲击, 2016, 36(6):745-751.
LIN Wen-zhou, HONG Tao. Numerical simulation of friction sensitivity of high explosives[J]. Explosion and Shock Waves, 2016, 36(6):745-751.(in Chinese)
[6] Hayden D W. An analytic tool to investigate the effect of binder on the sensitivity of HMX-based plastic bonded explosives in the skid test[D]. Socorro, NM, US: New Mexico Institute of Mining and Technology, 2004.
[7] 申春迎, 黄谦, 向永, 等. PBX炸药在滑道试验中的响应[J]. 四川兵工学报, 2015, 36(2):136-140.
SHEN Chun-ying, HUANG Qian, XIANG Yong, et al. Reaction behavior for PBX explosives in skid test[J]. Journal of Sichuan Ordnance, 2015, 36(2):136-140.(in Chinese)
[8] Rol B, Katrin B, Philip E, et al. Nanotribology-fundamental studies of friction and plasticity[J]. Advanced Engineering Materials, 2010, 12(5):362-367.
[9] Amuzu J K A, Briscoe B J, Chaudhri M M. Frictional properties of explosives[J]. Journal of Physics D: Applied Physics, 1976, 9(1):133-143.
[10] Bolotov A N, Strel’Nikov Y A. Effect of high hydrostatic pressure on the external friction coefficient[J]. Journal of Friction and Wear, 2012, 33(3):174-180.
[11] Zukas J A, Walters W P. Explosive effects and applications[J]. International Journal of Impact Engineering, 1998(5):417.
[12] Jiang X B, Guo S, Yao M, et al. Novel method for determining the dynamic friction coefficient of explosives[J]. Combustion, Explosion, and Shock Waves, 2014, 50(1):118-123.
[13] Hoffman D M, Chandler J B. Aspects of the tribology of the plastic bonded explosive LX-04[J]. Propellants Explosives Pyrotechnics, 2004, 29(6):368-373.
[14] Dickson P, Parker G, Smilowitz L, et al. Frictional heating and ignition of energetic materials[J]. AIP Conference Proceedings, 2006, 845(1):1057-1060.
[15] Durand B, Delvare F, Bailly P, et al. Friction between steel and a confined inert material representative of explosives under severe loadings[J]. Experimental Mechanics, 2014, 54(7):1293-1303.
[16] 赵继波, 李克武, 傅华, 等. 炸药与不同材料之间摩擦系数的研究[J]. 高压物理学报, 2014, 28(5):591-596.
ZHAO Ji-bo, LI Ke-wu, FU Hua, et al. Research on the friction coefficient between explosive and different materials[J]. Chinese Journal of High Pressure Physics, 2014, 28(5):591-596.(in Chinese)
[17] Sun B P, Duan Z P, Ma Z F, et al. Numerical simulation on frictional ignition of charge during projectile penetration[J]. Transaction of Beijing Institute of Technology, 2012, 32(8):771-775.
[18] 王晔, 白春华, 李建平. 弹壳体结构对燃料装药抛撒速率影响的数值模拟研究[J]. 兵工学报, 2017, 38(1):43-49.
WANG Ye, BAI Chun-hua, LI Jian-ping. Influence of shell structure on dispersing velocity of fuel-air mixture[J]. Acta Armamentarii , 2017, 38(1):43-49.(in Chinese)
[19] 吴林杰, 侯海量, 朱锡,等. 水下接触爆炸下防雷舱舷侧空舱的内压载荷特性仿真研究[J]. 兵工学报, 2017, 38(1):143-150.
WU Lin-jie, HOU Hai-liang, ZHU Xi, et al. Numerical simulation on inside load characteristics of broadside cabin of defensive structure subjected to underwater contact explosion[J]. Acta Armamentarii, 2017, 38(1):143-150.(in Chinese)
[20] 丁力, 蒋建伟, 门建兵, 等. 爆炸成型弹丸成型过程中的断裂数值模拟及机理分析[J]. 兵工学报, 2017, 38(3):417-423.
DING Li, JIANG Jian-wei, MEN Jian-bing, et al. Numerical simulation and mechanism analysis of EFP’s fracture in forming process[J]. Acta Armamentarii, 2017, 38(3):417-423.(in Chinese)
[21] 王晔, 白春华, 李建平, 等. 非对称云雾爆炸超压场数值模拟[J]. 兵工学报, 2017, 38(5):910-916.
WANG Ye,BAI Chun-hua, LI Jian-ping, et al. Simulation of explosion overpressure distribution for non-symmetry cloud detonation[J]. Acta Armamentarii, 2017, 38(5):910-916.(in Chinese)
[22] 赵梓君, 毕世华. BIC实验的数值模拟研究[J]. 北京理工大学学报, 2015, 35(6):556-559.
ZHAO Zhi-jun, BI Shi-hua. Numerical simulation on ballistic impact chamber test[J]. Transactions of Beijing Institute of Technology, 2015, 35(6):556-559.(in Chinese)
[23] Gibbs T R, Popolato A, Baytos J F. LASL explosive property data[M]. Los Alamos, NM, US: University of California Press, 1980.
MeasurementandModificationofDynamicFrictionCoefficientofPressedExplosive
LUO Yi, LIU Yan, HUANG Feng-lei
(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081,China)
In order to investigate the effect of dynamic friction coefficient on the friction ignition of pressed explosive, 8701 pressed explosive is tested on the friction testing system based on the drop hammer apparatus, and tthe coefficients of dynamic friction between 8701 pressed explosive and 45#steel at different normal pressures are studied. The experimental results show that, when the normal pressure is increased from 1 MPa to 10 MPa, the dynamic friction coefficient is reduced from 0.28 to 0.10, indicating that the dynamic friction coefficient is dependent on pressure. A calculation model of the friction coefficient is proposed based on the experimental results and introduced into the LS-DYNA through secondary development. The thermo-chemo-mechanical coupling numerical simulation is conducted for the skid test of 8701 pressed explosive. The calculated results show that the improved calculation model of friction coefficient prolongs the ignition delay time, increases the critical ignition velocity and raises the critical ignition temperature. The proposed model can be used to study the non-shock friction ignition problem.
ordnance science and technology; pressed explosive; friction coefficient; friction ignition; drop-hammer impact
2017-04-06
国家自然科学基金项目(11272059)
罗毅(1987—), 男, 博士研究生。 E-mail: luoyi@bit.edu.cn
刘彦(1975—), 男, 教授, 博士生导师。 E-mail: liuyan@bit.edu.cn
TJ410.3+41
A
1000-1093(2017)10-1926-07
10.3969/j.issn.1000-1093.2017.10.007
