某型航空发动机封严篦齿盘异型螺栓孔公差设计分析

殷良伟，郭海丁

（南京航空航天大学能源与动力学院，南京210016）

某型航空发动机封严篦齿盘异型螺栓孔公差设计分析

殷良伟，郭海丁

（南京航空航天大学能源与动力学院，南京210016）

为了有效降低孔边应力水平，以某型航空发动机封严篦齿盘5参量单轴对称异型孔为研究对象。针对此类异型孔的公差设计问题，利用蒙特卡洛模拟技术，通过构造异型孔孔边应力状态的响应面函数以对设计参数进行灵敏度分析,确定了需要给定公差的设计变量。讨论了异型孔的重要设计尺寸公差带对孔边应力分布及配合的影响，并参照美制紧固件螺栓通孔设计标准，确定了此类异型孔尺寸公差选取应满足的强度要求及装配等级。

异型孔；蒙特卡洛模拟；响应面；公差设计；航空发动机

0 引言

螺栓连接是航空发动机转子部件常见的连接方式。高压涡轮组件在高温、高转速下工作，载荷环境恶劣，而螺栓通孔孔边区域则是疲劳裂纹萌生的高发区[1-2]。为改善螺栓通孔孔边应力状态，国外某型航空发动机高压涡轮组件的封严篦齿盘及高压涡轮盘幅板上的螺栓通孔均采用异型螺栓孔来代替传统的圆型螺栓通孔。实践表明：采用异型螺栓通孔可有效地降低孔边应力及应力集中，有效提高结构的强度储备和安全裕度[3-4]。

国内从2012年起开始对异型孔的设计方法开展系统的研究[4-5]。研究主要围绕异型孔轮廓尺寸的设计方法进行，其中，文献[5]提出并建立了异型孔的数学模型及优化模型，对异型孔结构进行了尺寸优化。文献[4-5]的研究表明：异型孔轮廓设计参数选取恰当，可有效减小孔边应力。在采用了异型螺栓孔的2个部件（高压涡轮盘和封严篦齿盘）中，封严篦齿盘的螺栓通孔位于盘的辐板，对于此类异型孔的轮廓设计要求更为苛刻。尺寸公差的设置与加工、装配密切相关，也会对异型孔边应力状态带来一定影响。

本文将利用蒙特卡洛模拟建立孔边应力状态与设计参数的响应面方程，通过分析各个设计参数的灵敏度，分析设计尺寸公差的变化对异型孔孔边应力的影响，给出异型孔尺寸公差设置原则。

1 异型孔孔边应力状态响应面建模

螺栓连接及异型螺栓孔结构如图1所示。某型发动机高压涡轮转子组件局部螺栓连接结构如图1（a）所示，该组件由前鼓筒轴、封严篦齿盘和高压涡轮盘等3个部件组成，通过螺栓、托板螺母连接，螺栓预紧力为41187.16 N。高压涡轮盘前安装边的螺栓采用了双轴对称8段圆弧异型孔，如图 1（b）所示。封严篦齿盘辐板上的螺栓孔则采用了单轴对称8段圆弧异型孔，其轮廓尺寸如图1（c）所示。

从图中可见，该结构对其中部分尺寸给出了设计公差，说明对这些尺寸的控制要求更高。一般说来，工程结构的内力为结构尺寸的隐函数，难以直接分析尺寸变化对结构应力的影响。为了分析篦齿盘异型螺栓孔设计尺寸公差对孔边应力的影响，本文将结合有限元技术和蒙特卡洛模拟方法，构造孔边应力水平对5个设计参数的响应面函数。

1.1 含异型螺栓孔篦齿盘有限元模型

封严篦齿盘上的单轴对称异型孔物理模型如图2所示。从图中可见，该模型由8段圆弧构成。由于异型孔单轴对称，在设计时只需给出与5个圆弧有关的半径尺寸和相应孔的轮廓尺寸，在此称其为5参量异型孔。篦齿盘异型螺栓孔轮廓尺寸见表1。

表1 设计点处轮廓尺寸参数 mm

5参量异型孔关于Y轴对称，其短轴长度为2a=9.957 mm，与原螺栓通孔基圆直径大小相等以保证与螺栓配合，长轴长度为2b=10.262 mm。其中，R1、R2、R3为主圆弧半径，R4、R5为过渡圆弧半径，各圆弧光滑相切。

在进行有限元仿真时，取封严篦齿盘1/48扇形段简化模型进行循环对称分析。该模型采用自由分网、孔边网格加密，单元类型为solid185。模型材料为镍基高温合金GH4169；密度为8240 kg/m3；泊松比为0.37。篦齿盘工作转速为ω=14731 r/min。文献[4]的研究表明：扭矩对孔边应力状态的影响可以忽略不计，故分析中忽略辐板前后端面的摩擦力，并将接触应力简化为等效面载荷以提高计算效率[5-6]。在封严篦齿盘轮心施加轴向约束。

1.2 工作状态下的篦齿盘异型螺栓孔边应力状态分析

通过有限元计算得到篦齿盘异型螺栓孔边第1主应力如图3所示。从图中可见，孔边最大主应力区域位于孔边4点钟、8点钟位置附近，最大第1主应力值为742.84 MPa。在孔边6点钟和12点钟位置为轮盘径向开裂危险点，其最大第1主应力值分别为676.23、657.14 MPa，约为该处周向应力值。

Allison公司推荐的辐板最大周向许用应力值[7]为

式中：σs为0.2%屈服强度；ND为设计转速；NM为完整性试验转速；NM=118.4%ND。求得[σ]=691.23 MPa，由此可见设计点满足推荐应力标准[8]。

由于涡轮盘部件盘身辐板受离心力的影响，将辐板周向应力集中区作为高应力区，应该着重关注[9]。由于螺栓孔边径向开裂由孔边周向应力主导，而孔边周向应力值为孔边第1主应力值，故在之后的响应面函数构造中以孔边最大第1主应力、孔边6点钟位置第1主应力和12点钟位置第1主应力作为响应。

1.3 封严盘异型孔孔边应力的响应面函数构造

由于异型孔轮廓尺寸的变化导致孔边应力水平发生变化，其响应面模型能够反映各圆弧尺寸对孔边应力水平的影响。该模型可将5段圆弧半径作为模型的输入，孔边应力水平作为输出[10-12]。

响应面建模所需样本由蒙特卡洛方法模拟得到，以异型孔设计参数Ri(i=1,2,3,4,5)为输入变量，而孔边最大第1主应力σmax、在孔边6点钟方向第1主应力σ6c、在孔边12点钟方向第1主应力σ12c分别为3个响应。在随机抽样中，样本容量取500，设计变量取值范围与负公差带相似，样本在取值范围内均匀分布，其上限为XiH，下限为XiL，各设计变量取值范围见表2。

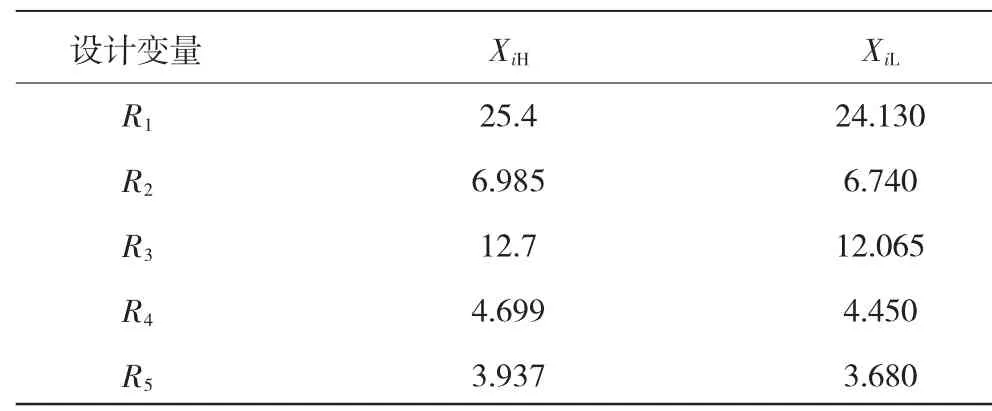
表2 设计变量取值范围 mm

由于设计变量之间数量相差偏大，为使响应面函数中的待定系数能够更好地反映响应对不同设计变量之间的相对关系，可对输入变量按下式进行归一化处理[12]

式（3、4、5）中：响应单位为MPa；输入变量单位为mm。

各应力相应拟合误差如图4所示。从图中可见，不同位置的所有拟合结果均位于有限元模拟值±3%误差带内，由此证明1阶响应面函数模型在负公差带附近有足够好的拟合精度。

2 异型孔设计变量灵敏度及公差分析

2.1 设计变量灵敏度分析

灵敏度分析是研究1个系统的响应随输入变量变化时的敏感程度的方法[14]，对于封严篦齿盘异型螺栓孔设计而言，那些对孔边应力响应敏感程度高的设计参数，在设计中应更加谨慎给出公差范围，提高部件设计的可靠性[15-18]。

分析异型螺栓孔边应力水平对各设计变量变化的灵敏度，可通过分析响应面函数模型，即式（3）～（5）中与各设计变量前的系数来确定。为设计变量前的系数对应力响应变化的灵敏度所占百分比如图5所示。

从图中可见，在所给的各设计变量变化范围内，R2、R5对孔边最大第1主应力值的变化贡献率最大，且R2为正相关，R5为负相关；R5对孔边6点钟位置第1主应力的变化贡献率最大，且为正相关，其次为R2，为负相关；R4对孔边12点钟位置第1主应力的变化贡献率最大，且为正相关。主圆弧R2、过渡圆弧R4、R5为重要设计尺寸。

2.2 公差分析

综合考虑孔边各个危险点处应力值与设计参数之间的相关性，R2、R4、R5减小有利于降低孔边应力水平，所以在尺寸公差设计时，应给定负公差控制，而主圆弧R1、R3对孔边应力变化的影响相对小，在设计与加工时的裕度较大，则不需要设置公差来保证加工精度。这个分析印证了图2原设计中尺寸公差设计的合理性。

3 紧固件螺栓通孔设计标准与异型螺栓孔尺寸公差分析

3.1 紧固件螺栓通孔设计标准

在国标（GB）、航标（HB）以及美国标准（ANSI）等各国标准中，紧固件螺栓均有3种装配等级，分别为精装配（close）、中等装配（normal）、粗装配（loose），对应某螺栓标准件可用的3种标准螺栓通孔孔径。这种确定圆孔加工公差的方法对异型孔而言并不适用。由于异型孔的引入，增大了孔的轮廓，减少了螺栓孔周围区域连接件之间的接触面积，孔的扩大将对提供可靠的预紧力和传递扭矩带来不利影响[19]。对异型孔设计尺寸设置负公差时，过渡圆弧尺寸的减小将导致异型螺栓孔轮廓面积增加，连接单元的接触面积进一步减小，螺栓孔轮廓尺寸比较如图6所示。

为评估不同配合条件下螺栓通孔轮廓对螺栓连接接触区面积的负面影响，定义螺栓装配等级参量P1对其进行评估。P1定义

式中：As为ANSI标准螺栓通孔轮廓面积，Ac为异型孔基圆（直径2a）轮廓面积。P1越大，表明实际承载面积越小。

如图1（b）所示涡轮组件的连接螺栓为公称直径为9.525 mm（3/8”）的12角法兰面螺栓，篦齿盘异型孔螺栓孔基圆直径为9.957 mm。与该美制螺栓相应的3种装配等级的圆形通孔直径及对应的P1值见表3。

表3 ANSI中3种装配方式与对应的P1值 mm

从表中数据可见，中等装配时P1n接近于1，说明基圆螺栓孔与ANSI标准中等装配标准圆孔面积相近，而P1l则小于ANSI标准粗装配。在异型孔公差设计时，为保证可靠的承载面积（传扭和预紧）应至少保证公差带内异型孔轮廓面积不大于粗装配螺栓通孔面积，即使得异型孔与螺栓的配合至少满足与基圆粗装配同样的要求，如此可以保证承载和传力的需要。

3.2 异型螺栓通孔负公差带分析

为确定异型螺栓孔重要尺寸的公差带选取范围，可综合蒙特卡洛抽样分析关键尺寸对孔边应力的影响及装配精度来确定。以下仅取有负公差带约束的圆弧半径为R2、R4、R5为输入变量，其响应不变，分别在关键尺寸Ri（i=2,4,5）原有负公差带k倍区间内均匀抽样（k=2,3,4,5），定义 k 倍区间上限 XikH=XiL-（k-2）（XiH-XiL），下限为 XikL=XiL-（k-1）（XiH-XiL），样本容量均为500。由于区间内应力水平十分接近，故选取区间内平均应力值为代表，与设计点应力值进行比较。计算结果见表4。

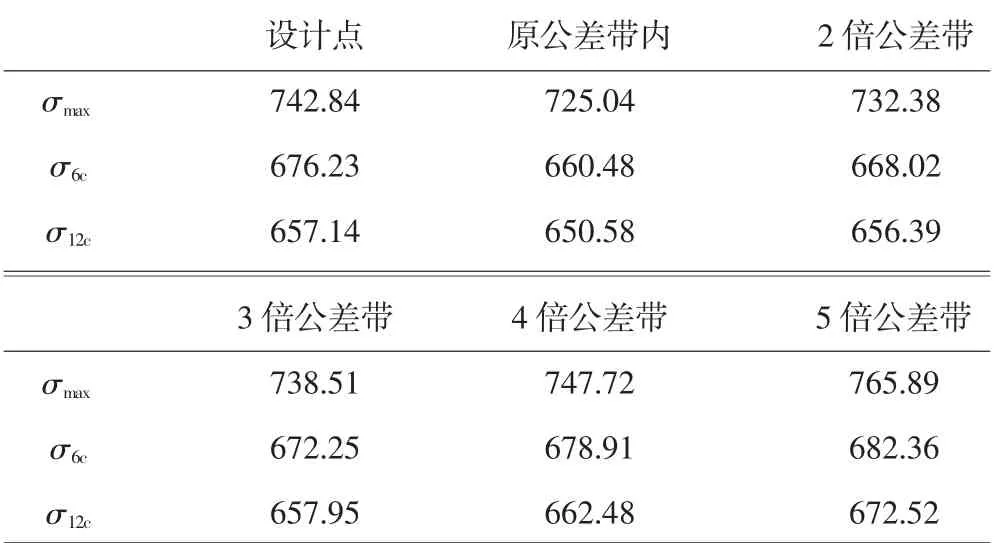
表4 设计点与负公差k倍区间内平均应力对比（k=2,3,4,5）MPa

通过比较可知：在原有负公差带至3倍负公差带区间内，孔边平均应力水平均低于设计点应力值，且在3倍负公差带时，平均应力水平与设计点应力值最为接近。当尺寸负公差为设计负公差4～5倍时，孔边平均应力水平比设计点处应力值上升。负公差带附近应力水平变化趋势如图7所示，从图中可见，坐标横轴为原设计公差带倍数k，原点为设计点尺寸；纵轴为区间内平均应力值，单位为MPa。

从图中可见，虽然3倍公差带范围内应力值均能满足设计要求，但只有在原有负公差带内应力水平呈下降趋势，设计点附近应力水平极小值位于设计负公差带下限点附近，越过负公差带边界后应力水平则呈上升趋势。不难看出，原设计负公差带为设计点附近应力值下降段，且在负公差带边界时，应力水平最低，能够保证其强度安全裕度。

3.3 异型螺栓孔装配精度分析

异型螺栓孔除需满足应力要求外，还需保证与螺栓配合的部分承载和传扭要求。为此定义

P2可以评估异型螺栓孔轮廓增大对螺栓连接接触区面积的负面影响。异型孔P2值见表5。其中基圆轮廓面积为77.86 mm2。

比较表3、5数据之后可知，若异型孔设计参数R2、R4、R5尺寸在原有负公差带内，则 1.0144＜P2＜1.0207＜P1粗，即异型孔与螺栓的配合至少能满足以基圆孔设置的粗装配要求（表3中，基圆粗配合P1c=1.0362），保证较小的承载面损失和足够的传扭面积；若圆弧R2、R4、R5的尺寸小于负公差带下限，则异型孔轮廓面积将继续增大，在下公差达到3倍原设计公差下限点时P2=1.0433＞1.0362，即大于（表3中）基圆粗装配要求的比值P1c。此时，虽然孔边应力水平与设计点相当，仍能满足孔边最大应力要求，但异型螺栓孔轮廓面积变大，孔边配合面积减小，无法保证美制螺栓通孔设计标准中粗装配精度，从而对连接单元传力带来不利影响。由此可见，原构件异型孔设计在选取公差时，除了需要保证孔边应力不上升外，还应保证配合面积满足提供螺栓预紧力和接触面摩擦力要求。综合上述考虑，在进行航空发动机盘异型螺栓孔公差带设计时，选用公差带应从满足规定装配精度和产品的加工制造能力出发，选取合理的公差尺寸：公差选取应在保证孔边应力下降到设计值的同时，考虑开孔后的周围配合面积应满足提供螺栓预紧力和接触面摩擦力的要求，既可保证异型孔结构满足了孔强度安全裕度的要求，又不会对开孔结构的传力带来影响。

表5 异型孔与基圆孔轮廓面积与P2值

4 结论

通过对某型封严篦齿盘异型螺栓孔的重要设计尺寸公差对孔边应力状态的影响分析，结合螺栓通孔设计标准讨论了该型涡轮盘异型螺栓孔重要设计尺寸中负公差带的选取原则，得到结论如下：

（1）所研究的篦齿盘异型螺栓孔孔边最大应力对设计变量R2、R4、R5最为敏感，应考虑设置合理的公差带，在加工制造中则应严格控制；而设计变量R1、R3的设计裕度较大。

（2）在篦齿盘异型孔设计时，可定义异型孔与圆孔装配等级参量来确定螺栓装配等级，异型孔轮廓关键尺寸的负公差带内异型孔与螺栓的配合应至少满足基圆粗装配精度，即达到与圆形基圆通孔粗装配相近的配合面积标准。

（3）在异型螺栓孔轮廓尺寸公差设计中，应同时考虑异型孔边危险点处强度要求和螺栓通孔装配精度要求，从而既能保证异型孔孔边应力不高于设计值的，又能使得孔边配合区域面积能满足螺栓预紧和接触面摩擦力要求。

[1]杨俊，李承彬，谢寿生.涡轮盘多轴低循环疲劳寿命预测及试验验证[J].航空动力学报，2011,26（10）：2220-2226.YANG Jun,LI Chengbin,XIE Shousheng.Multiaxial cycle fatigue life prediction and test verification for turbine disk [J].Journal of Aerospace Power,2011,26(10):2220-2226.(in Chinese).

[2]陆山，黄其青.涡轮盘销钉孔损伤容限分析方法及其应用[J].航空动力学报，2002,17（1）：87-92.LU Shan,HUANG Qiqing.New method for damage tolerance analysis of turbine disk and its application [J].Journal of Aerospace Power,2002,17（1）:87-92.(in Chinese).

[3]SHIYongjiu,WANG Meng,Analysison shearbehaviorof high-strength bolts connection[J].International Journal of Steel Structures,2011,11（2）:203-213.

[4]张超.涡轮连接单元异型孔应力场分析及结构优化.[D].南京：南京航空航天大学，2014.ZHANG Chao.Stress field analysis and structural optimization of non-circular hole on flange of turbine disks[D].Nanjing:Nanjing University of Aeronautics of Astronautics,2014.（in Chinese）.

[5]陈秋任.涡轮盘异型孔设计与优化 [D].南京：南京航空航天大学，2013.CHEN Qiuren.Structural design and optimization of non-circular hole on turbine disks[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2013.（in Chinese）.

[6]杨山林，虞慧岚，薛金星，等.U型伸缩臂下滑块厚度调整对接触应力影响研究[J].起重运输机械，2014（4）：74-76..YANG Shanlin,YU Huilan,XUE Jinxing,et al.Analysis on the influence of thickness on contact stress of bottom slide block of the U-shaped telescopic boom [J].Lifting the Transport Machinery,2014（4）:74-76.（in Chinese）.

[7]Allison公司.Turbine Mechanical Design Criteria.GMA400 Engine,AX,0400-171[S].1978.

[8]《中国航空材料手册》编辑委员会编.中国航空材料手册.变形高温合金、铸造高温合金[M].北京：中国标准出版社，2001:328-331.Editorial Committee of China Aeronautical Materials Handbook.China aeronautical materials handbook:wrought superalloy and cast superalloy[M].Beijing:Standards Press of China,2001:328-331.（in Chinese）

[9]SPEY MK202发动机应力标准（EGD-3）[S].北京：国际航空编辑部，1979：9-11.SPEY MK202 engine stress standard（EGD-3）[S].Beijing:International Aviation Editorial Department,1979：9-11.（in Chinese）

[10]王桂华，井海龙，史妍妍，等.基于响应面法的齿轮容差设计方法研究[J].航空发动机，2016（6）:3-4.WANG Guihua,JING Hailong,SHI Yanyan,et al.Methods of tolerance for gears based on response surface methodology[J].Aeroengine,2016,42（6）:3-4.（in Chinese）

[11]余治民，刘子建，董思科,等.基于蒙特卡洛模拟和响应面方法的公差建模[J].中国机械工程，2015（4）:427-431 YU Zhimin,LIU Zijian,DONG Sike,et al.Tolerance modeling based on Monte-Carlo simulation and response surface method[J].China Mechanical Engineering,2015（4）:427-431.（in Chinese）.

[12]熊俊涛.基于响应面方法的气动优化设计 [D].西安：西北工业大学，2005.XIONG Juntao.Aerodynamic optimization design technology based on response surface method[D].Xi’an:Northwestern Polytechnical University,2005.（in Chinese）.

[13]陈乐，刘继炜，强天鹏，等.CR工艺参数对不锈钢焊接裂纹检出率的影响[J].南昌航空大学学报，2015,29（2）：63-64.CHEN Le,LIU Jiwei,QIANG Tianpeng,et al.Influence of stainless steel weld crack detection rate with different process parameters for computed radiography[J].Journal of Nanchang Hangkong University,2015.29（2）:63-64.（in Chinese）.

[14]熊俊涛，乔志德，韩忠华.基于响应面法的跨声速气动优化设计[J].航空学报，2005,27（3）：399-402.XIONG Juntao,QIAO Zhide,HAN Zhonghua.Optimum aerodynamic design of transonic wing based on response surface methology[J].Chinese Journal of Aeronautics,2005,27（3）:399-402.(in Chinese)

[15]王新刚，张义民，王宝艳.机械零部件的动态可靠性灵敏度分析[J].机械工程学报,2010（10）:189-191.WANG Xingang,ZHANG Yimin,WANG Baoyan.Dynamic reliability sensitivity analysis of mechanical components[J].Journal of Mechanical Engineering,2010（10）:189-191.(in Chinese).

[16]陈秋任，郭海丁，刘小刚.涡轮盘双轴对称异型孔结构建模与优化[J].航空动力学报，2013（6）:1251-1256.CHEN Qiuren,GUO Haiding,LIU Xiaogang.Modeling and optimization for the structure of biaxial symmetry non-circular hole of turbine disk[J].Journal of Aerospace Power,2013（6）:1251-1256.（in Chinese）.

[17]杨周，杜尊令，张义民.某型航空发动机涡轮盘的可靠性灵敏度设计[J].东北大学学报，2011,32（8）：1162-1164 YANG Zhou,DU Zunling,ZHANG Yimin.Reliability based sensitivity design of an aero-engine turbine disk[J].Journal of Northeastern University,2011,32（8）:1162-1164.（in Chinese）.

[18]张义民，王鹏，杨周，等.低周疲劳失效的涡轮盘可靠性灵敏度设计[J].中国机械工程，2010，21（10）：1135-1139 ZHANG Yimin,WANG Peng,YANG Zhou,et al.Reliability sensitivity design for a turbine disc with low cycle fatigue failure[J].Chinese Journal of Mechanical Engineering,2010;21 （10）:1135-1139.（in Chinese）.

[19]彭铁红，侯兆欣，文双铃，等.螺栓孔径与孔型对高强度螺栓摩擦型连接承载能力影响的试验[J].钢结构，2007,22（8）：30-34.PENG Tiehong,HOU Zhaoxin,WEN Shuangling,et al.Experiment of effects hole diameter and hole type on bearing capacity of high strength bolt frictional joints[J].Steel Construction,2007,22（8）:30-34.（in Chinese）.

[20]The American Socienty of Mechanical Engineers.Unified Screw Threads（UN and UNR Thread Form）[S].New York:The American Society of Mechanical Engineers，1989:6-8.

Analysis on Dimension Tolerance Design of Non-circular Hole of Labyrinth Disk for an Aeroengine

YIN Liang-wei，GUO Hai-ding
（College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China）

In order to reduce efficiently the stress level,a five-parameter non-circular clearance hole of the labyrinth disk was taken as the research object.Aiming at the dimension tolerance design of non-circular hole,the response surface functions of the stresses near the hole were built to conduct sensitivity analysis for the design parameters using the Monte Carlo Simulation method,and the design variables which need appending tolerances were determined.The influences of the most important design dimension tolerances zone of the non-circular hole on stress distribution and coordination of the hole edge were discussed,and the selection of dimension tolerance of the non-circular hole that meets the requirement of both strength and the assembly specifications of ANSI is determined.

non-circular hole;Monte Carlo Simulation;response surface;tolerance design;aeroengine

V 232.3

A

10.13477/j.cnki.aeroengine.2017.05.001

2017-01-12

殷良伟(1993)，男，在读硕士研究生，主要研究方向为结构强度与完整性；E-mail:ylw597620061@hotmail.com

殷良伟，郭海丁.某型航空发动机封严篦齿盘异型螺栓孔公差设计分析[J].航空发动机，2017，43（5）：85-90.YIN Liangwei，GUO Haiding.Analysis dimension tolerance design of non-circular hole of labyrinth disk for an aeroengine[J].Aeroengine，2017，43（5）：85-90.

（编辑：张宝玲）