基于效用和均值-方差准则的多人随机微分博弈

杨 鹏, 惠小健, 刘 琦

(西京学院 理学院, 陕西 西安 710123)

基于效用和均值-方差准则的多人随机微分博弈

杨 鹏, 惠小健, 刘 琦

(西京学院 理学院, 陕西 西安 710123)

以3人为例研究多人随机微分博弈，其中2人为相互合作的投资者，另一人为2投资者博弈的“虚拟”对手——金融市场.研究2种情形的随机微分博弈，一种情形为基于效用的博弈，另一种为基于均值-方差准则的博弈.对于第一种情形，2个投资者的目标是使终值财富的期望效用达到最大，金融市场的目标是使该期望效用最小.对于第二种情形，2个投资者的目标是在终值财富的期望给定时使终值财富的方差最小，金融市场的目标是使方差最大.应用随机控制理论求得2个博弈问题的最优投资策略、最优市场策略、最优值函数的显式解.通过研究，可以指导相互合作的两投资者在金融市场情况恶劣时，选择恰当的投资策略使终值财富的期望效用最大，或使自身获得一定的财富而面临的风险最小.

幂效用； 均值-方差准则; 随机微分博弈; 投资

博弈论是一门古老的学科，但是文献[1]的发表才标志着现代博弈论的开始.随机微分博弈是博弈论的一个重要分支，它主要研究决策者随时间变化的相互作用的决策过程.文献[2]首次将数学模型用于随机微分博弈之中.之后很多人沿着文献[2]的方向研究随机微分博弈问题.如今，随机微分博弈已成为数理金融和经济学的一个重要研究分支.

近年来基于投资组合最优化的随机微分博弈，成为一个研究热点.文献[3]考虑了连续时间模型下2个有着不同但相关投资机会的投资者之间的零和随机微分投资组合博弈.文献[4]研究了在马氏调制模型下，以最小化风险为目标的两投资者之间的零和随机微分博弈.文献[5]研究了保险公司在跳-扩散模型下面对一个未知模型的投资组合选择问题.文献[6]在指数效用下研究了扩散风险模型的最优再保险和投资问题.他们通过求解最优控制问题对应的HJBI方程，得到了最优再保险、投资策略、最优市场策略和值函数的显示解.文献[7]应用线性-二次控制的理论，研究了负债情形下投资者与市场之间的随机微分博弈.在投资者具有指数效用和幂效用下，求得了最优投资组合策略、最优市场策略和值函数的显式解.

已往文献对随机微分博弈的研究大多数都是基于效用的,很少研究基于均值-方差准则的随机微分博弈.文献[8]对于扩散风险模型，研究了基于均值-方差准则的随机微分博弈.利用线性二次控制理论得到了最优策略和有边界的显示解.文献[9]研究了资产负债情形下基于均值-方差准则的随机微分博弈，和文献[8]类似地得到了最优策略和有边界的显示解.然而，很少有学者研究多人微分博弈.因此，本文研究了3人随机微分博弈的投资组合选择问题.3人中其中2人为投资者，另一人为这2个投资者竞争的“虚拟”对手——金融市场，两投资之间是合作关系.基于投资者和金融市场之间的随机微分博弈的投资组合选择已有很多学者研究，如文献[5-7]等.本文考虑了有2个投资者的情况，这给研究带来了一定的困难.本文在幂效用函数下通过猜出解的形式，对解的形式应用It公式，通过进一步计算得到了最优策略和值函数的显式解.另外，本文还把随机微分博弈和均值-方差投资组合选择问题联系了起来.与文献[8-9]相似，本文研究的问题转化后，成为基于幂效用随机微分博弈问题中p=2的情况.这样，就进一步得到了原基于均值-方差准则随机微分博弈问题的最优策略和有效边界.本文的结果也可推广到有n(n>2)人的情况，我们只要把n人分成2组即可.本文的研究还可以考虑推广到CEV模型、Heston模型、Vasicek模型等更一般的模型，这些问题将在以后进一步研究.

1 模型的建立

为了使数学上更为严格,假设所有的随机过程和随机变量都定义在完备的概率空间(Ω,F,P)上,并且有一满足通常条件的σ-流{Ft,t≥0},即Ft右连续且P完备.W1(t)、W2(t)是概率空间上2个相关系数为ρ的标准布朗运动.考虑一个金融市场，由3个金融资产组成，其中一个是无风险资产(债券),时刻t的价格{Bt,t≥0}满足方程

dBt=rBtdt，

其中r>0为无风险利率.2个风险资产(股票)，在时刻t的价格Si(t)满足随机微分方程

dSi(t)=Si(t)[μidt+σidWi(t)]，

其中,μi≥r,σi>0为常数,i=1,2.

有2个投资者，投资者A和投资者B，投资者A只能在无风险资产和第一种风险资产上投资；投资者B只能在无风险资产和第二种风险资产上投资.设πi(t)分别为两投资者在时刻t在风险资产上投资的比例，则考虑投资后两投资者的财富过程Xi(t)满足下面的随机微分方程

dXi(t)=Xi(t)[r+(μi-r)πi(t)]dt+Xi(t)πi(t)σidWi(t),i=1,2.

(1)

定义1一个策略πi(t)称为可行的，如果πi(t)关于流Ft是可料的，且对于t≥0过程πi(t)满足下面的条件:

2) 随机微分方程(1)有唯一的强解.

所有可行的策略记为π.

注1假设X(0)=x0.(2)式考虑的是有2个投资者共同作用的财富过程，不同于有一个投资者投资到2个风险资产和无风险资产的情况.若有一个投资者，财富过程应为下面的方程

dX(t)=X(t)[r+(μ1-r)π1(t)+(μ2-r)π2(t)]dt+X(t)[π1(t)σ1dW1(t)+π2(t)σ1dW2(t)].

(3)

显然(2)式和(3)式是不一样的，因此它们对应的最优策略是不一样的.文献[7]研究了有n个投资者带负债的随机微分博弈,本文只针对(2)式进行研究,通过本文的研究对相互合作的投资者进行投资时会有一定的指导意义.

设{θ(t),t≥0}是定义在概率空间(Ω,F,P)上实值的满足下列条件的随机过程：

1) {θ(t),t≥0}是Ft循序可测的；

2) 对几乎所有的(t,ω)∈[0,+∞)×Ω,θ(t)=θ(t,ω)<1；

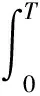
对满足上述条件的全体θ(t)记为Θ(t).

这里{θ(t),t≥0}代表了金融市场选择的经济环境，显然(2)式及风险资产价格过程的概率分布都依赖{θ(t),t≥0}的选择，同时{θ(t),t≥0}也体现了模型的不确定性因素.下文中研究2投资者和金融市场选择的经济环境之间的博弈.对每个{θ(t),t≥0}定义{Zθ(t),t≥0}如下

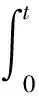
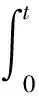
dZθ(t)=-Zθ(t)θ[dW1(t)+dW2(t)],Zθ(0)=1,

(4)

因此Zθ(t)是(Ft,P)上的局部鞅，因为{θ(t),t≥0}满足Novikov条件，所以Zθ(t)是(Ft,P)上的鞅，则

EZθ(T)=EZθ(0)=1.

2 基于效用的随机微分博弈

考虑一个严格递增严格凹的效用函数u，即u′<0,u″>0.记XT为终值时刻T时2个投资者的共同财富，对每一个可行策略π1、π2，定义两投资者的终值财富在Pθ下的期望效用为

Vπ1,π2,θ(t,x)=Eθ[u(XT)|Zθ(t)=z,X(t)=x],

其中Eθ是在市场策略θ下的期望.2投资者和市场进行如下的博弈，金融市场选择一个策略θ最小化Vπ1,π2,θ(t,x)，投资者A和投资者B分别选择策略π1、π2最大化金融市场的选择，即如下问题

(5)

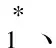
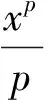
引理1f′(t)+pf(t)l=0,f(T)=1,则f(t)=epl(T-t).

证明引理1给出来的是常微分方程,比较容易求解.求解过程略.

定理1(5)式定义的随机微分博弈问题的最优投资策略为:

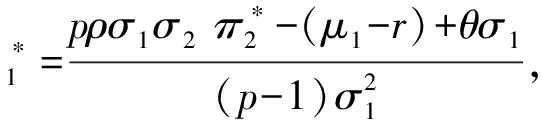
(6)

(7)

(8)

值函数为

(9)

从t到T上求积分，在Zθ(t)=z,X(t)=x的条件下在概率测度Pθ下取条件期望，结合引理1应用Beyes准则，得到

因为f(t)>0,Zθ(t)>0，所以问得证.证毕.

3 基于均值-方差准则的随机微分博弈

2个投资者的目的是，在终值财富的均值EXT=k时，在市场出现最坏的情况下找到一个最优投资策略使终值财富的方差VarXT最小.该问题称为基于均值方差准则的随机微分博弈.可描述如下.

定义2基于均值-方差准则随机微分博弈的投资组合选择问题是以参数k∈R为限制的随机最优化问题，也就是

(10)

其中(X(·),π1(·),π2(·))满足(2)式,Eθ是在概率测度Pθ下的期望.

下面将求解(10)式定义的问题的最优策略和有效边界.受文献[9-10]的启发可以引入拉格朗日乘子λ把(10)式做如下变形

其中(X(·),π1(·),π2(·))满足(2)式,λ前面添了数字2是为了下面处理方便.注意到(10)和(11)式是不等价的，要通过求(11)式的最优策略和有效边界得到(10)式的最优策略和有效边界.(11)式求得最优策略和有效边界后，应用对偶定理可得到(10)式的最优策略和有效边界.显然问题(11)等价于下面的问题

(12)

其中(X(·),π1(·),π2(·))满足(2)式.受文献[8]的启发，可以对g(t)[X(t)-(k-λ)]2Zθ应用It公式.但是如果这些做的话会出现[X(t)-(k-λ)]X(t)这样一些项，处理起来不方便.这里能不能把[X(t)-(k-λ)]看作一个整体呢？这是可以的.令Y(t)=X(t)-(k-λ),则Y(t)满足下面的随机微分方程

(13)

接下来，先求解如下微分博弈问题的解

(14)

定理2(12)式定义的随机微分博弈问题的最优投资策略为

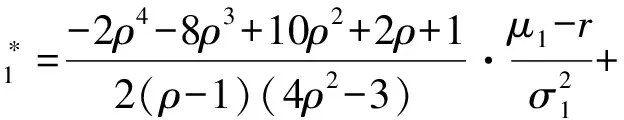
(15)

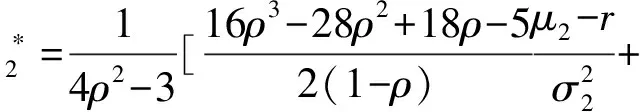
(16)

最优的市场策略为

(17)

有效边界为

(18)

因为Y(t)=X(t)-(k-λ)，所以有:

X(t)=Y(t)+(k-λ),

X(0)=Y(0)+(k-λ),

因此有

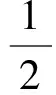
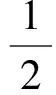
因此对于固定的λ有

V2(t,x(t),λ)=2V3(0,y(0),λ))-λ2,

所以

(19)

其中

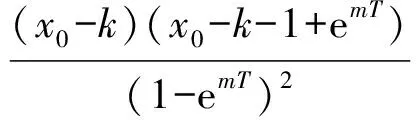
(20)

[1] VON NEUMANN J, MORGENSTERN O. The Theory of Games and Economic Behavior[M]. Princeton:Princeton University Press,1944.

[2] ISAACS R. Differential Games[M]. New York:John Wiley & Sons,1965.

[3] BROWNE S. Stochastic differential portfolio games[J]. Journal of Applied Probability,2000,37(1):126-147.

[4] ELLIOT R J, SIU T K. On risk minimizing portfolios under a markovian regime switching Black-Scholes economy[J]. Annals of Operations Research,2010,176(1):271-291.

[5] LIN X, ZHANG C H, SIU T K. Sotchastic differential portfolio games for an insurer in a jump-diffusion risk process[J]. Mathematical Methods of Operations Research,2012,75(1):83-100.

[6] 罗琰,杨招军. 基于随机微分博弈的保险公司最优决策模型[J]. 保险研究,2010(8):48-52.

[7] 杨鹏. 随机微分博弈下的资产负债管理[J]. 中山大学学报(自然科学版),2013,52(6):30-33.

[8] 杨鹏,刘琦. 基于均值方差随机微分博弈的再保险和投资[J]. 四川师范大学学报(自然科学版),2016,32(2):248-253.

[9] 杨鹏,王震,孙卫. 均值-方差准则下具有负债的随机微分博弈[J]. 经济数学,2016,33(1):25-29.

Stochastic Differential Gamer for Multiple Decision MakersBased on Utility and Mean-variance Criterion

YANG Peng, XI Xiaojian, LIU Qi

(SchoolofScience,XijingCollege,Xi’an710123,Shaanxi)

Taking an example of three people, stochastic differential game between multiple decision makers is studied. Two of them are the mutual cooperation investors and the last one is the two investors “virtual” opponents-the financial markets. Two kinds of stochastic differential games are studied, one is the game based on utility and the other one is based on the mean-variance criterion. For the first case, the goal of two investors is to make the expected utility of the final value wealth maximum, the financial market goal is to minimize the expected utility. For the second case, the two investor target is to minimize the variance of the terminal value of wealth with a given final expected value. For financial markets the goal is to make the variance of financial markets maximum. By applying stochastic control theory, we obtained the optimal investment strategy, the optimal market strategy and the explicit solution of the optimal value function two game problems. Our result can guide the choice of appropriate investment strategy in the mutual cooperation of the two investors in the financial market to maximize the expected utility of the final wealth, or to minimize risk for wealth for themselves.

power utility; mean-variance criterion; stochastic differential games; investment

2016-05-18

陕西省自然科学基础研究项目(2016JM1024)

杨 鹏(1983—),男,讲师,主要从事随机微分博弈和数理金融的研究,E-mail:yangpeng511@163.com

F830; O225

A

1001-8395(2017)05-0655-06

10.3969/j.issn.1001-8395.2017.05.016

2010MSC: 91B30

(编辑 周 俊)