Besov空间中一类反周期函数的三角插值逼近问题

何尚琴， 冯秀芳

(1. 宁夏大学 数学计算机学院, 宁夏 银川 750021;2. 河北科技师范学院 数学与信息科技学院, 河北 秦皇岛 066004)

Besov空间中一类反周期函数的三角插值逼近问题

何尚琴1,2， 冯秀芳2

(1. 宁夏大学 数学计算机学院, 宁夏 银川 750021;2. 河北科技师范学院 数学与信息科技学院, 河北 秦皇岛 066004)

引进一种插值算子，研究在Besov空间中以2π为周期的反周期函数的三角插值的逼近阶和饱和问题，确定了逼近的饱和类.

反周期三角插值算子； Besov空间； 饱和类

函数逼近论是现代数学的一个重要分支，其研究目标是用简单的可计算函数对一般函数进行逼近，进而考虑其逼近的程度和如何刻画被逼近函数本身的特性.插值多项式可看作实现逼近的一个重要工具，其中三角多项式插值是函数逼近论的重要研究方法.以2π为周期函数的三角插值已有深入的研究及推广[1-2],A.Sharma等[3]研究了2π周期函数的(0,m)三角插值，A.S.Cavaretta等[4]研究了2π周期函数的(0,m1,m2,…,mp)三角插值.但其插值空间Tn,ε(x)对平移运算和求导运算不封闭，从而2π周期函数的三角插值问题在实际应用中受到一定的限制.反周期函数的(0,m)三角插值问题的研究自文献[5]的研究之后受到广泛关注[6-7].以2π为周期的反周期函数三角插值问题对上述2种运算封闭，因而研究以2π为周期的反周期函数的三角插值有重要意义.Besov空间中插值算子的研究在近些年来发展很快.文献[8]研究了在Besov空间中，Jackson整插值算子的逼近和饱和问题，确定了逼近的饱和类与饱和阶.文献[7]得出了三角插值算子在Besov空间中逼近的饱和类与饱和阶.本文研究Besov空间中以2π为周期的反周期函数三角插值多项式逼近的饱和问题，确定了逼近的饱和类.

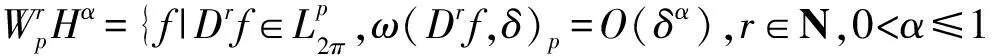
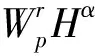
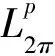
则g(x)叫作f(x)的m次Lp范数，记作g=Drf.

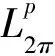
(1)

当插值核Kn(x)取Fejer核时，Jn(f,x)就是著名的Jackson插值算子[9-13],它满足插值条件：

取文献[6]中定理1中的ρ0=0,

则当

时，易知当m为奇数时(1)式定义的三角插值多项式Jn(f,x)满足插值条件：

1 引理

引理1[6]若T(x)为2n-1阶反周期三角多项式，则一定存在常数aj、bj,使得

其中

.

由引理1及引理2易得以下引理：

引理3设

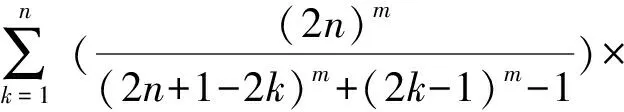
得

‖Rn(x)‖1=O(1).

引理4[15]对任意n阶三角多项式Tn(x)有

引理6设Tn(x)为2n-1阶反周期三角多项式，f(x)是以2π为周期的反周期函数,若

有

证明当n=2k+1时有

由引理3有

于是

所以，对任意的n∈N存在k∈N,当2k-1≤n≤2k+1时得

2 主要结果

证明充分性 记n′=2n-1,k=2j-1,由引理2可得

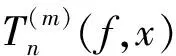
其中,xk满足

因

故

从而

必要性 由假设知

运用引理5得

于是

由三角多项式的性质知Tn(Tn(f))=Tn(f),则有

存在常数C>0,使得

又

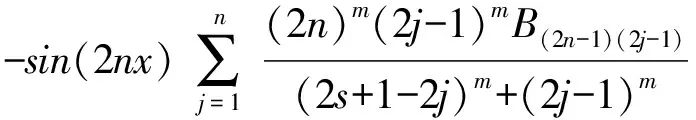
其中

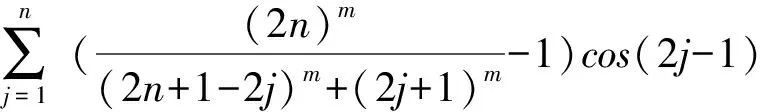
由引理4得

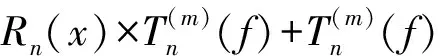
从而

因

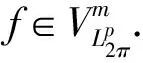
由引理5知

因此当k→∞时得

致谢宁夏大学自然科学研究基金(ZR16035)对本文给予了资助，谨致谢意.

[1] HAN X L. Piecewise trigonometric Hermite interpolation[J]. Appl Math Comput,2015,268(10):616-627.

[2] GAO W W, WU Z M. A quasi-interpolation scheme for periodic data based on multiquadric trigonometric B-splines[J]. J Comput Appl Math,2014,271(1):20-30.

[3] SHARMA A, VARMA A K. Trigonometric interpolation[J]. Duke Math J,1965,32(1):341-357.

[4] CAVARETTA A S, SHARMA A, VARGA R S. Lacunary Trigonometric Interpolation on Equidistant Nodes in “Quantitative Approximation”[M]. New York:Academic Press,1980:63-88.

[5]STEPANETS A L. Lacunary interpolation by antiperiodic trigonometric polynomials[J]. BIT,1999,39(3):430-450.

[6] 何尚琴,侯象乾. 反周期函数三角插值的收敛性[J]. 宁夏大学学报(自然科学版),2006,27(3):218-224.

[7] 文晓霞. 一类反周期函数的双周期缺项插值问题[J]. 江西师范大学学报(自然科学版)，2014，38(1)：62-64.

[8] 赵振宇,侯象乾. Jackson整插值算子在Besov空间中的逼近[J]. 华中师范大学学报(自然科学版),2002,36(4):413-415.

[9] 赵振宇,侯象乾. 一类三角插值多项式在Besov空间中的逼近[J]. 数学研究,2005,38(3):260-264.

[10] 刘永平. 一类三角多项式插值算子的逼近性质[J]. 东北数学,1988,4(3):289-308.

[11] 谢庭藩,周颂平. 实函数逼近论[M]. 杭州:杭州大学出版社,1998.

[12] SZABADOS J, VERTESI P. Interpolation of Functions[M]. Singapore:World Scientific,1990.

[13] STEPANETS A L. Classification and Approximation of Periodic Functions[M]. London:Kluwer Academic Publishers,1995.

[14] 李风军,侯象乾,李星. 一类三角插值多项式在Besov空间的逼近[J]. 内蒙古师范大学学报(自然科学汉文版),2004,33(3):267-271.

[15] 嘉德克B K. 多项式一致逼近函数导论[M]. 沈燮昌,方企勤,娄元仁,等译. 北京:北京大学出版社,1989:233.

Problem on a Kind of Anti-periodic Trigonometric Interpolation Approximation in Besov Space

HE Shangqin1,2, FENG Xiufang2

(1.SchoolofMathematicsandComputerScience,NingxiaUniversity,Yinchuan750021,Ningxia;2.CollegeofMathematicsandInformationScienceandTechnology,HebeiNormalUniversityofScienceandTechnology,Qinhuangdao066004,Hebei)

Using a kind of interpolation operator, we study the 2 periodic trigonometric interpolation approximation and saturation problem of antiperiodic functions in Besov space, and determine the approaching saturation class.

antiperiodic trigonometric interpolation operator; Besov space; saturation class

2016-04-12

国家自然科学基金(11161036)

何尚琴(1977—)，女，博士生，主要从事函数逼近论、偏微分方程数值解法的研究，E-mail:hsq101@163.com

O174.41

A

1001-8395(2017)05-0628-04

10.3969/j.issn.1001-8395.2017.05.011

2010MSC:03F50

(编辑 李德华)