基于最小二乘法的无线充电线圈自感辨识

郭丽莎，罗志超，魏学哲

(同济大学汽车学院，上海 201804)

基于最小二乘法的无线充电线圈自感辨识

郭丽莎，罗志超，魏学哲

(同济大学汽车学院，上海 201804)

提出了一种基于最小二乘法的新型线圈自感辨识方法，以发射端和接收端电路串联的电压型无线能量传输(即充电)系统为例，建立其非线性高阶微分方程并构建数据矩阵，通过最小二乘法获得系统的过程参数矢量，将线圈的自感辨识问题转换为系统参数辨识问题，完成无线充电系统发射端和接收端线圈的自感辨识，最后通过仿真和实验，验证了该方法的可行性。

线圈自感；无线能量传输；最小二乘法；参数辨识

前言

减少交通运输领域的能源消耗和尾气排放是环境保护的一个重要环节。在这种背景下，发展电动汽车，是世界公认的缓解能源短缺和环境污染的有效策略，而对于我国又显得至关重要[1]。目前电动汽车安全充电问题成为制约其进一步推广的一个主要原因。电动汽车和有线充电桩问世并逐步推广使用，但这种充电方式需要使用充电电缆连接充电机和电动汽车，存在操作繁琐、可靠性与安全性差等问题，而无线充电供电灵活安全、取电方便、无电气连接的特点完美解决了有线充电的这些缺陷，并且环境适应能力强，在雨雪天气等潮湿的环境也可正常使用，能够有效促进电动汽车大规模推广应用[2-3]。

为降低电动汽车无线充电耦合机构工作时对非工作区域内电磁环境的影响，提高耦合效率，并增强无线充电系统工作的稳定性，需要对电动汽车无线充电过程中的空间电磁能量进行约束，并对无线充电耦合机构进行磁屏蔽。目前常用的方法是在耦合机构外加上铁氧体材料[4-6]。加入磁屏蔽材料之后，当上下线圈错位时，线圈的自感发生变化，发射端和接收端的电路不再谐振。此时，系统的阻抗明显增大，能耗增加，效率降低。此外，当线圈的自感发生变化，需要根据自感的变化来调节系统的频率或进行阻抗匹配，以提高系统效率，自感辨识是其关键问题。因此，为了建立更加高效、稳定和可靠的无线能量传输系统，自感的辨识问题亟待解决。然而系统的高阶非线性使自感的辨识问题成为一个瓶颈。

本文中基于最小二乘法提出一种新型的自感辨识策略。以SS结构(即发射端和接收端的线圈与其补偿电容皆为串联)的电压型无线能量传输系统为例，通过建立系统非线性高阶微分方程完成对矩阵的构建，并在此基础上利用最小二乘法完成对系统过程参数的辨识，通过过程参数矢量和自感间的线性关系完成对自感的辨识，将直接对自感的辨识问题转化为对系统参数的辨识问题[7]。最后通过仿真分析验证了此方法的可行性和准确性，是一种简便、易于实现的自感辨识方法。

1 线圈自感的变化

RLC串联电路如图1所示，电路的总阻抗为

当阻抗的虚部为零，即电路谐振时

此时，电路的虚功消耗为零，系统的效率最高。而当发射端电路和接收端电路的线圈自感发生改变，在同一个频率下，发射端电路和接收端电路不可能同时达到谐振，无线充电系统总是有虚功消耗，使系统的能量传输效率明显下降。所以，明确线圈的自感，为以后的系统调节提供信息基础，是无线充电系统实际应用中必须解决的问题。

图1 RLC串联电路

2 主电路拓扑

谐振器是无线充电装置的核心模块，由一对非接触耦合线圈及其匹配电路组成，如图2所示。发射线圈将交变电流转化为空间中交变磁能，同在空间近处的接收线圈通过交变磁场产生感应电压，在负载上产生电流，完成能量从发射线圈到接收线圈的传递。该系统由发射电路和接收电路两个独立部分组成。图中电压源us(t)提供整个系统的电能输入，Cs为发射端电容，Ls为发射线圈的自感，Rs为发射端电阻，Cd为接收端电容，Ld为接收线圈的自感，Rd为接收端电阻，Cf为滤波电容，r为负载端的电阻，b为电池负载。

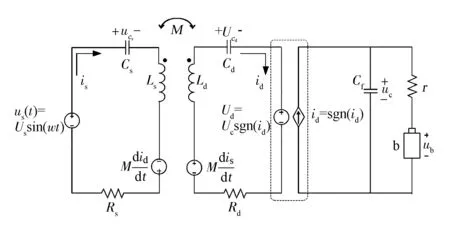
图2 主电路与拓扑结构

将系统模型进行简化，结合无线充电系统特有的负载特性，研究无线充电应用中的控制方法。车用无线充电系统针对普通家庭应用进行设计，能量源为220V的交流电，负载为300V车用动力电池组。将负载简化为一个电阻，采用纯电阻负载进行系统特性研究，其电路模型如图3所示。

图3 简化的电路图

3 线圈自感的辨识

3.1 基于最小二乘法的参数辨识

由该系统可获得差分方程为

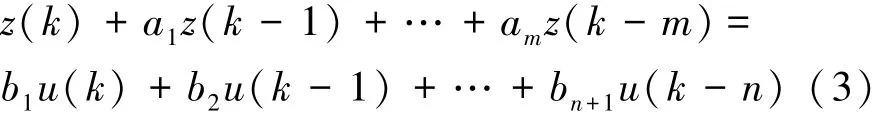
式中：z(k)为系统输出量的第k次观测值；z(k-1)为系统输出量的第k-1次观测值，以此类推；u(k)为系统的第k次输入值；u(k-1)为系统的第k-1次输入值。

可以将上式改写为

由于k存在一系列取值，因此可进一步将式(4)改写为最小二乘的矩阵形式：

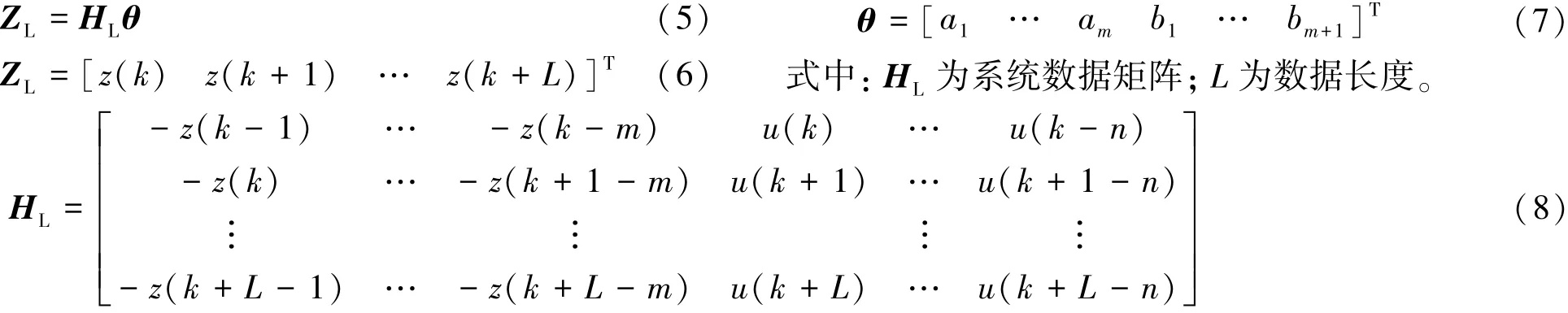
取准则函数

显然，可通过最小二乘法，得到过程参数矢量θ的最小二乘估计为

此时，辨识得到过程参数矢量θ＾与系统参数(如电阻、电感、电容)之间存在线性关系，通过对线性方程进行分解变换，便可获得发射线圈和接收线圈的自感信息，完成线圈自感的辨识。

3.2 系统矩阵的构建与自感辨识

通过无线充电系统的磁耦合谐振器的数学模型建立系统非线性高阶微分方程，并完成对数据矩阵的构建。构建过程如下：首先选取发射端的谐振电流is，初级谐振电压ucs，次级谐振电流id，次级谐振电压ucd，滤波电容电压uc为状态变量，建立瞬态状态空间方程。

引入符号函数sgn(x)对整流桥进行简化，将谐振器的负载电压表达为相位受谐振电流控制，幅值被滤波电容钳位，电压源ud＝ucsgn(id)。 将整流桥的输出电流表示为idsgn(id)。 可以得到谐振器与滤波电路的瞬态状态空间方程为

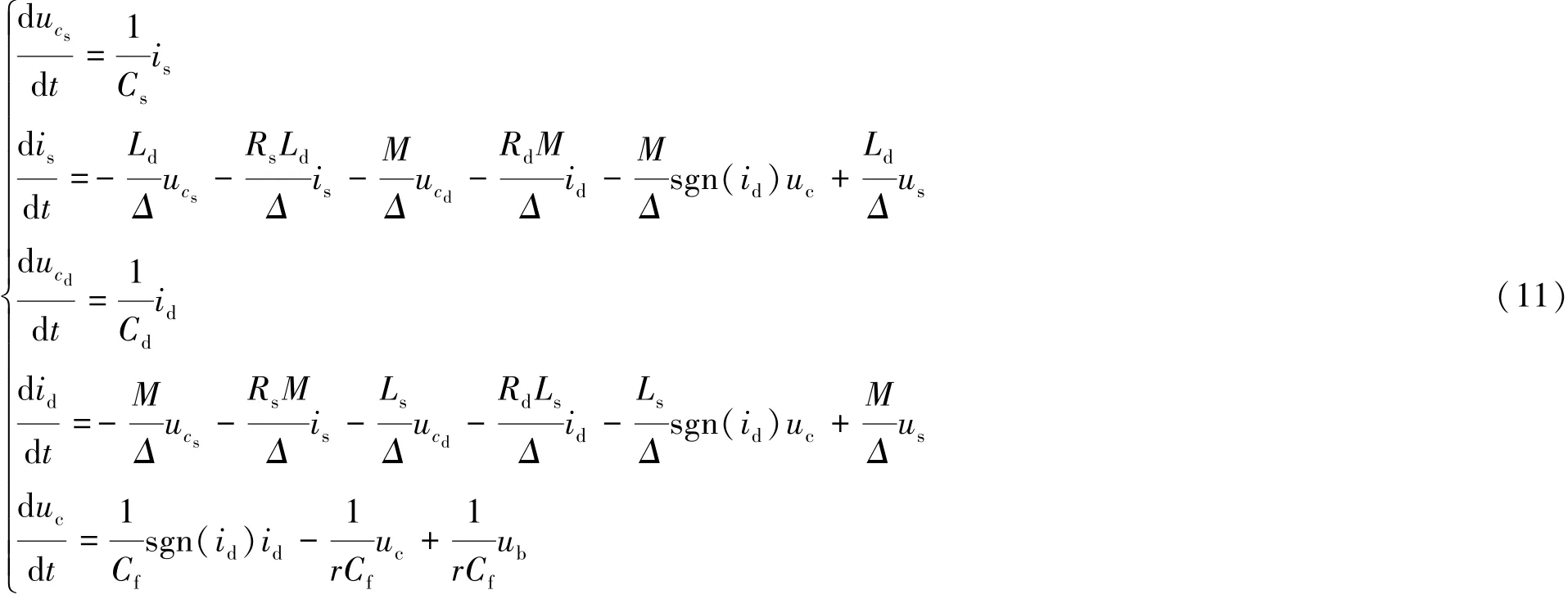
其中Δ＝LsLd-M2，sgn(x)为符号函数：

对简化后的谐振器电路的状态空间方程进行拉普拉斯变换可以得到

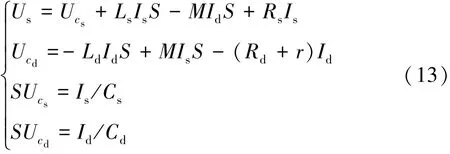
解方程可以得到Id(s)与Us(s)之间的关系为

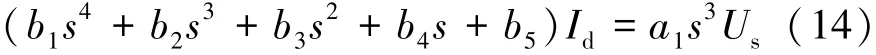
进而获得如下传递函数：

为获得更为精准的系统离散模型，经过分析比较选用双线性离散的方法对传递函数进行离散化处理。离散化处理之后得到：

式中c＝2/T，T为采样周期。

将离散化后的传递函数进行反变换可以构建出

该系统的一组差分方程：

最终可以得到该系统的数据矩阵和过程参数矢量：

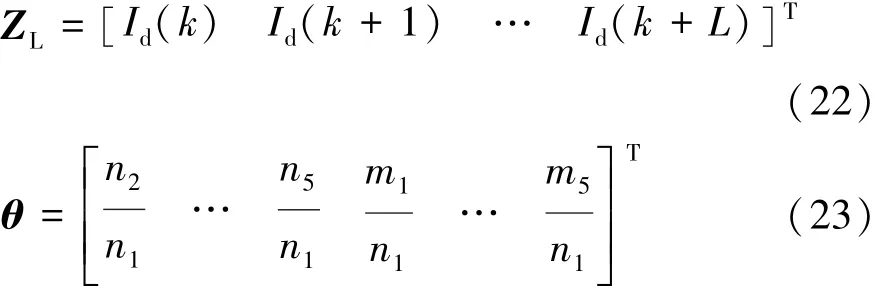
以发射线圈和接收线圈的自感分别为150和

由上述公式可以用最小二乘辨识方法辨识得到过程参数估计值θ＾。由于系统中互感可以在线检测出来，电容及寄生电阻等均为已知值，并且输入的电压值和输出的电流值都可以检测得到。因此可以较容易获得参数估计值θ＾和发射线圈Ls与接收线圈Ld之间的关系进而求得线圈自感，完成线圈自感的辨识。

4 辨识结果

为验证本文中提出的负载辨识方法，基于Matlab/Simulink仿真平台建立系统仿真模型，其主要参数如表1所示。180μH，170和200μH为例进行仿真验证。

表1 系统参数

输入电压波形图如图4所示。

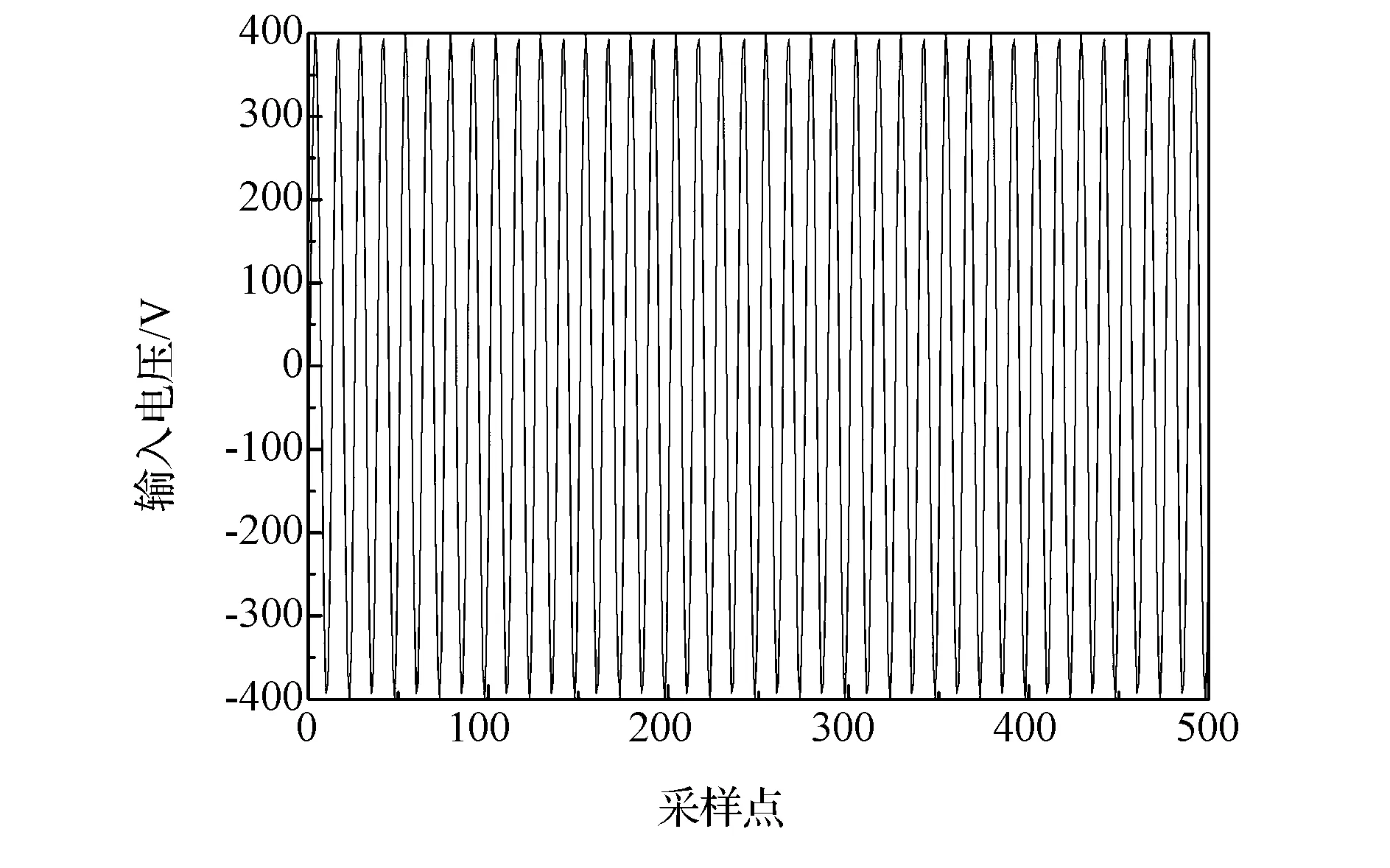
图4 输入电压波形图

输出电流波形图如图5所示。

图5 输出电流波形图

对输入电压和输出电流进行采样，采样时间间隔为1×10-6s，采集2 000个点，分别进行辨识。辨识结果如表2所示。

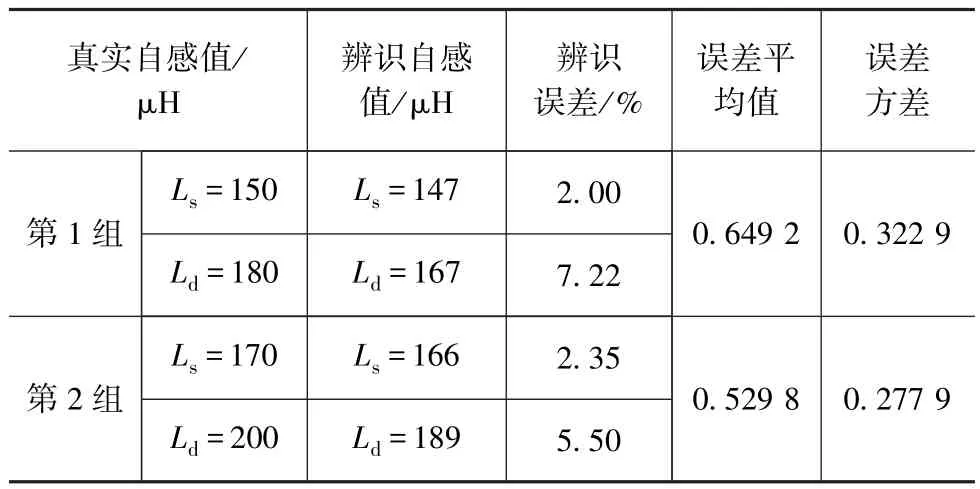
表2 辨识结果

第1组数据，将辨识结果带入系统得到的输出电流与真实电流的结果对比如图6所示。

图6 第1组结果对比

第2组数据，将辨识结果带入系统得到的输出电流与真实电流的结果对比如图7所示。

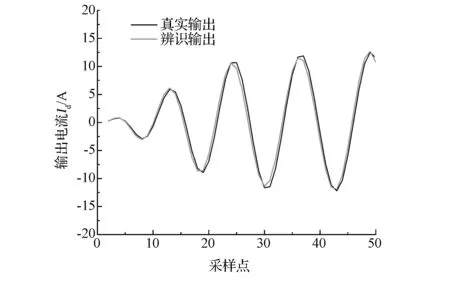
图7 第2组结果对比

5 实验验证

由于输入400V的高压进行实验具有很高的危险性，并且需要辨识的线圈自感不受输入电压幅值影响，所以通过输入幅值为10V的正弦交流电来验证该方法的可行性。所搭建的实验台架见图8。

图8 实验台架

通过LCR仪测得发射线圈和接收线圈的自感均为134μH。

实验选取的主要器件参数如表3所示。

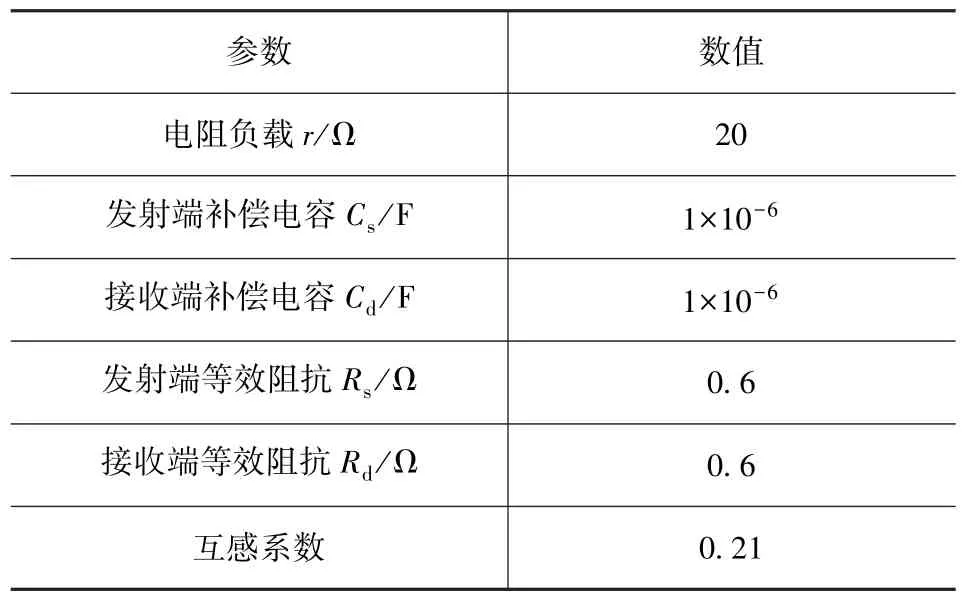
表3 实验参数

由数据采集卡采集到输入电压值和接收线圈的电流值，分别作为该辨识算法的输入和输出，通过最小二乘辨识方法得到发射线圈和接收线圈的电感值。采集输入电压值和仿真电压值的对比，如图9所示。采集输出电流值和仿真电流值的对比，如图10所示。

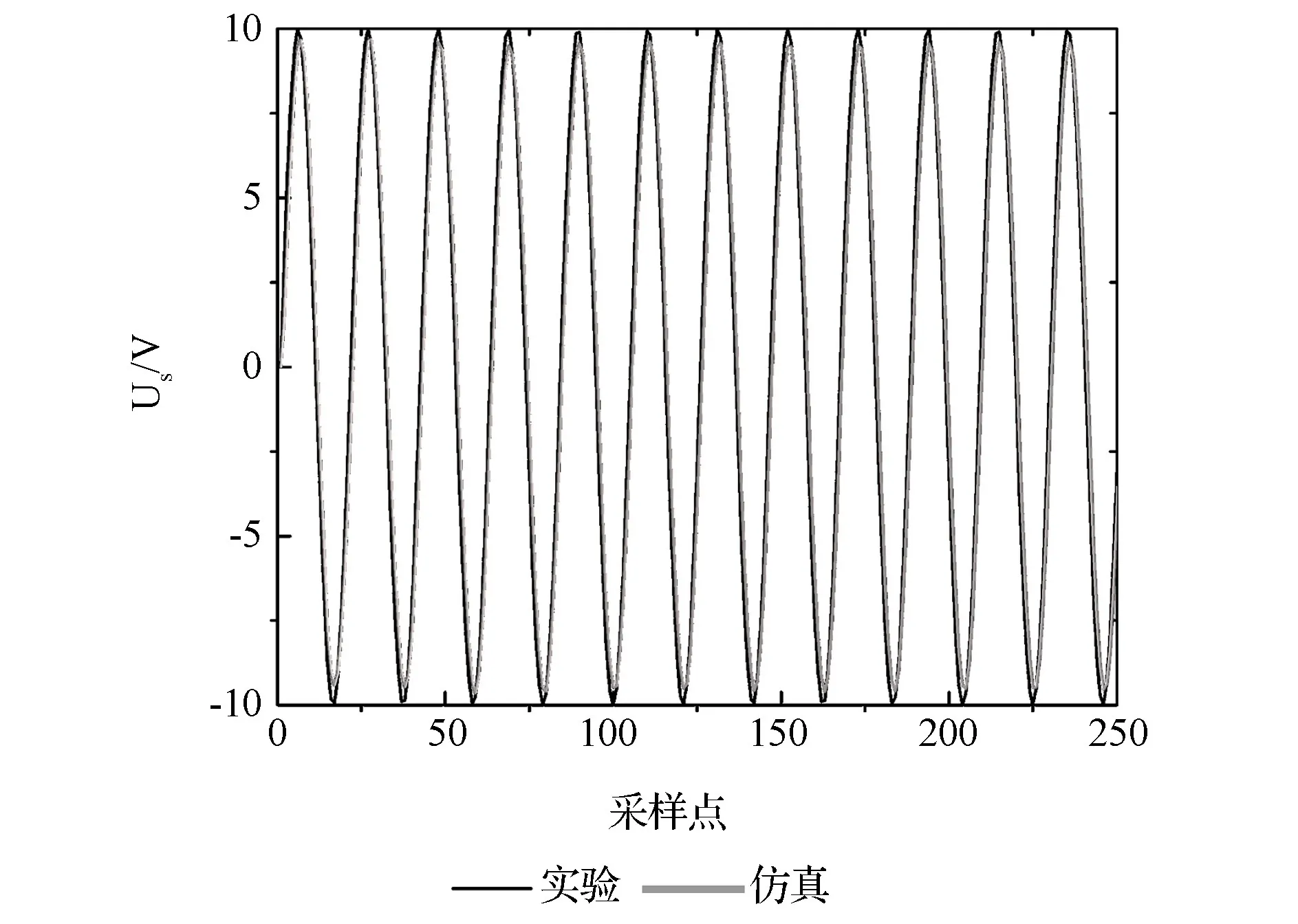
图9 输入电压对比

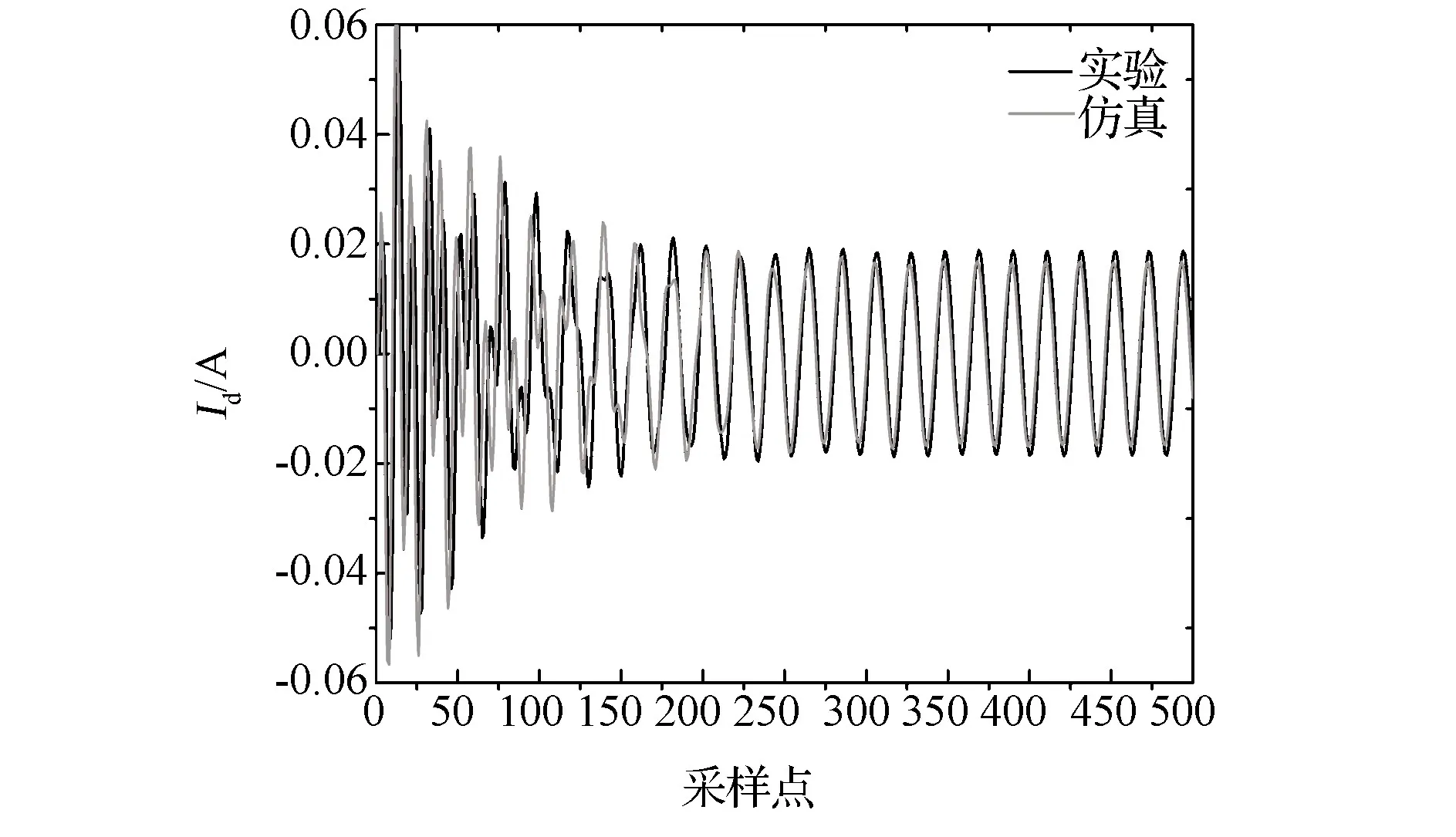
图10 输出电流对比

通过最小二乘辨识方法得到发射线圈和接收线圈的电感值。实验结果如表4所示。

表4 实验结果

6 结论

通过无线能量传输系统进行建模分析，完成其数据矩阵的构建，并以此为基础利用最小二乘法完成对线圈自感的辨识。针对加入磁屏蔽材料之后线圈自感发生变化，而线圈的自感无法测量与计算的问题，提出一种简便可靠的线圈自感的辨识方法。仿真结果和实验结果表明，该方法具有较高的准确度，误差在可接受的范围内。该方法对于提高无线充电系统的效率有重要的参考意义，为其他类型的无线能量传输系统的自感辨识提供借鉴。通过参数辨识的方法明确线圈的自感之后，可以根据该自感来进行阻抗匹配或频率控制，提高系统的能量传输效率。当简化的系统的线圈自感辨识达到要求精度后，再将简化的系统还原来辨识自感。该算法采用单一频率的激励对参数的变化较敏感，可以通过改进的最小二乘法进一步提升辨识的精度，如采用频谱更宽的输入信号，以改善对系统的激励；采用扩展或广义最小二乘法对采样信号进行更好的处理。

[1] 曹玲玲，陈乾宏，任小永，等.电动汽车高效率无线充电技术的研究进展[J].电工技术学报，2012，27(8)：1-13.

[2] 张建.中频磁共振式电动汽车无线充电系统设计与效率优化[D].长春：吉林大学，2015.

[3] 黄学良，谭林林，陈中，等.无线电能传输技术研究与应用综述[J].电工技术学报，2013，28(10)：1-11.

[4] 陈德清，王丽芳，廖承林，等.无线充电系统损耗分析及磁体结构优化[J].电工技术学报，2015(s1)：154-158.

[5] BUDHIA M，COVIC G A，BOYS JT.Design and optimization of circular magnetic structures for lumped inductive power transfer systems[J].IEEE Transactions on Power Electronics，2011，26(11)：3096-3108.

[6] 张献，章鹏程，杨庆新，等.基于有限元方法的电动汽车无线充电耦合机构的磁屏蔽设计与分析[J].电工技术学报，2016，31(1)：71-79.

[7] 陈金干.基于模型的动力电池参数估计研究[D].上海：同济大学，2009.

The Identification of the Self-inductance in Wireless Charging Coils Based on Least Square Method

Guo Lisha，Luo Zhichao＆ W ei Xuezhe
School of Automotive Studies， Tongji University， Shanghai 201804

A novel identification scheme of coil self-inductance based on least squaresmethod is proposed.Taking voltage type wireless power transmission(WPT)system，namely charging system，with series transmitter and receiver circuits as an example，a nonlinear high-order differential equation is established with its data matrix constructed.Then the process parameter vectors of the system are obtained by least squaremethod，and the problem of coil self-inductance identification is converted to a problem of system parameter identification，and the self-inductance identification of transmitter and receiver coil in WPT system is completed.Finally，the feasibility of the scheme proposed is verified by simulation and test.

coil self-induction； WPT； least squaremethod； parameter identification

10.19562/j.chinasae.qcgc.2017.10.019

原稿收到日期为2017年3月23日，修改稿收到日期为2017年5月31日。

魏学哲，教授，博士生导师，E-mail：weixzh＠ tongji.edu.cn。