珠江河口拉格朗日拟序结构及其在浊度锋识别中的应用

詹伟康，韦 惺，叶海彬，詹海刚

(1. 热带海洋环境国家重点实验室，广东 广州 510301; 2. 中国科学院大学，北京 100049)

珠江河口拉格朗日拟序结构及其在浊度锋识别中的应用

詹伟康1,2，韦 惺1，叶海彬1，詹海刚1

(1. 热带海洋环境国家重点实验室，广东 广州 510301; 2. 中国科学院大学，北京 100049)

基于珠江河口水文实测资料和三维水动力数值模型，利用有限时间李雅普诺夫指数提取分析了流场中的拉格朗日拟序结构(LCSs)，并结合卫星遥感图像探讨珠江河口LCSs时空分布与其浊度锋的关系。结果显示，河口浊度锋与LCSs在时空上存在很好的契合，LCSs所形成的输运通道与壁垒对河口浊度锋的位置、形态及变化过程有显著影响。落潮时，泥沙随蕉门、洪奇门和横门的落潮射流注入伶仃洋，与虎门下泄的冲淡水对峙形成了一条明显的FTLE脊线，制约着浊度锋的形成和分布形态。涨潮时，来自西北三口门的淡水径流受口门外涨潮流的顶托作用，强烈的水平速度与密度梯度在此处形成LCS，阻碍径流挟带悬浮泥沙的输运而产生浊度锋。由于LCSs很好地勾画了不同动力性质的水体边界，因此可以用来对河口浊度锋进行识别、追踪和动力解释。

浊度锋；拉格朗日拟序结构(LCSs)；数值模拟；珠江河口

Abstract: Based on data measured in-situ, we extract and analyze Lagrangian Coherent Structures (LCSs) by calculating Finite Time Lyapunov Exponents of the flow field produced by a three-dimensional hydrodynamic numerical model, to study the relationship between LCSs and turbidity fronts of the Pearl River Estuary (PRE). Results show that the distribution of turbidity fronts are strongly tied to the simulated LCSs, which uncover fluid barriers that separate regions of different dynamics, and thus dominate the distribution and variation of the fronts. During the ebb tide, suspended sediment carried by the fresh water run-offs of Jiaomen, Hongqimen and Hengmen empties into the Lingding Sea through the west shoal. Meanwhile, however, the run-off of Humen from the north is much stronger than that of the other three. A prominent fluid dynamical boundary is therefore generated at the place the two kinds of run-offs meet, consequently shaping turbidity fronts. During the flood tide, significant horizontal velocity gradient and density gradient arise at the place where the freshwater run-offs of the three gates in the northwest Lingding Sea and flood current meet, leading to a remarkable LCS that impends the transport of suspended sediment, and thus a turbidity front. LCSs delineate fluid domains with quite different advective properties well. Therefore, we can locate and identify the variation of the fronts and obtain its generation mechanism by LCSs.

Keywords: turbidity front; lagrangian coherent structures(LCSs); numerical model; Pearl River Estuary

河口锋是指两种或多种具有明显不同水体之间的狭窄过渡带。其间的水平梯度可用水温、盐度、密度、叶绿素a以及悬浮泥沙等特征参数来确定。浊度锋为河口锋面现象类型之一，最初是由Kirby and Parker[1]在研究英国Severn河口的细颗粒泥沙过程中提出。浊度锋面存在时，有清晰的清浑水界面，锋面两侧有较大的悬沙浓度梯度，并伴随着明显的泡沫或污染物的积聚。

自20世纪70年代以来，中外学者已通过现场观测[2-4]、实验室分析实验[5]、数值模拟[6]、放射性示踪剂跟踪测定[7]等多种技术和方法对河口浊度做了大量的研究工作。20世纪90年代海洋水色遥感的兴起(AVHRR、TM、SeaWiFS、MODIS以及MERIS等)，实现了对全球海域的大面积同步连续观测，大大推动了河口浊度研究工作的发展[8-12]。然而，由于现场采样、实验分析和数值模拟等具有主观性和客观局限性，这些方法的适用性和精度不可避免地会受到影响。目前，遥感反演与监测仍是研究河口浊度变化机制的主流手段，但受水汽及其它大气气溶胶的影响，遥感亦不能保证对同一区域全天候的观测，以致出现数据缺测或数据质量不高等情况。为克服这些缺点，本文采用一种更具客观性和实用性的方法去探讨河口浊度锋。近来的研究表明，时变动力系统中基于拉格朗日分析而识别出的流体拉格朗日拟序结构(Lagrangian Coherent Structures，LCSs)对物质的混合及输运有很好的揭示作用[13-15]。利用LCSs可以很好地识别流体动力边界，并解释流体的水平输运现象。目前，LCSs理论已被广泛应用至海洋和近岸水域，如中尺度海洋搅拌和混合的描述[16-17]、海洋及近岸污染物的扩散与管理[18-21]、大洋及河口的水平平流输运[22-23]以及海洋生物的追踪及预报等[24-25]。

基于现场观测资料和珠江河口三维水动力模型，通过计算有限时间李雅普诺夫指数(FTLE)提取分析流场中的LCSs，并结合高分辨率卫星遥感图像探讨珠江河口LCSs与浊度锋分布及产生机制的关系。

1 资料与方法

1.1研究区域

图1 珠江河口地形图及水文观测站点分布Fig. 1 Map of the Pearl River Estuary and locations of hydrological stations

珠江河口位于中国南部，毗邻南海，是一个极具特色的大尺度河口[26]，其水域面积约2 000 km2，呈倒喇叭型分布，北部最窄区域(虎门附近)宽约4 km，南部宽(香港与澳门之间距)约60 km，整个珠江河口南北长度约63 km，见图1。珠江河口水深在0～30 m之间，平均水深小于5 m，其中西部浅滩区域水深在2～5 m之间。在地形上，有两条南北向深槽分别位于东西两侧，东槽为矾石水道，西槽为伶仃水道。珠江流域中的淡水及泥沙主要通过八大口门输入伶仃洋和南海。在亚热带海洋季风气候的影响下，珠江河口入海水沙表现出明显的季节性变化。洪季(4～9月)来水、来沙量占全年的78%～82%。其中悬沙主要由粉砂和粘粒构成。

珠江河口潮型为不正规半日潮，潮流多为往复流，由于受喇叭地形的影响，潮振幅自口外向口内的虎门方向递增，一天当中有两次涨落潮，平均潮差为0.86～1.63 m，最大潮差不到3.5 m[27]，整体潮汐动力较弱。但不同区域动力条件差异较大：虎门潮差较大，潮汐动力较强：磨刀门则相反，径流最强，潮差最小。受径流、潮流、季风和南海近岸环流等综合影响，珠江河口的水动力环境呈现复杂的时空变化性。

1.2数据资料

珠江河口水污染研究项目(Pearl River Estuary Pollution Project，PREPP)[28]于1999年7月17至27日在珠江河口实施了两次航测调查，各监测站点分布见图1。本研究模式结果流场验证用到其7个连续站点(C1～C7)，另有4个实测潮位站的数据用于验证水位。其中连续站的监测项目除了温盐外，还包括从表层到底层的分层流速流向数据，其监测频率为每小时1次。

Landsat-7号陆地卫星于1999年4月15日由美国航空航天局(NASA)发射升空，携带的主要传感器为增强型主题成像仪(Enhance Thematic Mapper Plus，ETM+)，具有8个波段，第1～4波段是可见光和近红外波段，第5和第7波段为短波红外波段，空间分辨率为30 m，第6波段是热红外波段，空间分辨率为60 m，同时传感器还带有一个空间分辨率为15 m的全色波段，单景图像幅宽185 km，且对全球同一地区的扫描周期为16天。本文利用Landsat7卫星波段数据(空间分辨率为30 m)合成珠江河口真彩色图像，真实地呈现河口悬浮泥沙及浊度锋的分布特征，结果为LCSs提供对比分析。

1.3数值模型

本文利用MIKE3模拟研究区域的水动力环境。MIKE3是由丹麦水利研究院(DHI)研发的水动力学模型，可用于模拟河流、湖泊、水库、大型河口和外海的水利、水质和泥沙传输问题[29-31]。

基于三维不可压缩的雷诺平均Navier-Stokes方程，MIKE3模式的三维浅水方程如下所示：

式中：(u,v,w)分别指代直角坐标系x，y和z三个方向上的速度分量；η为海表高度；d为静水深度；h=η+d为总水深；f为科氏参数；g为重力加速度；ρ为水的密度；ρ0为海水参考密度；vt为垂直湍流粘度(涡粘度)；pa为大气压强；(sxx,sxy,syx,syy)为辐射应力张量的分量；(Fu,Fv)分别为x，y方向上的水平应力；S指代由点源排放强度而定义的量级；(us,vs)指代水体被排放到邻近水体的速度。

模式的三维温度以及盐度输运方程如下：

图2 模型计算区域、网格和初始边界Fig. 2 Unstructured triangular grid and boundaries of MIKE3 for the simulated area

模型计算区域包括整个珠江河口及其外海海域，见图2。考虑到河口海岸地区底形变化较为剧烈，模型垂向采用Sigma坐标，分为11层。为更好地拟合局部岸线及岛屿的细节特征，提高近岸浅水区的模拟精度，模型采用渐变型非结构三角形网格，平面网格单元数为13 758个，网格分辨率在河口及沿岸区域较高，最高分辨率约为3 m，外海开边界处分辨率约为900 m。模型中考虑了径流、潮汐、风及底摩擦等因素，且采用干湿边界处理技术。其中陆域边界径流资料取自各水文观测站多年实测的月平均数据，外海开边界潮汐考虑8个主要分潮，M2、S2、K2、N2、K1、P1、O1及Q1，资料从全球潮汐数值模式(TMD: Tide Model Driver)计算得到。风场取洪季5～7月平均的东南风，风速4 m/s，风向130°。模型水下地形依据数字化海图(1997～2000年)而得，底床粗糙高度取0.05 m。模型从1999年5月1日起算，运行85天，并对计算结果进行分析。

1.4拉格朗日拟序结构(LCSs)

在时变动力系统中，LCSs可简单定义为一些可识别的物质输运轨迹结构[13]。这种轨迹结构具有物质线的性质，即理想情况下穿过它们的流体通量可忽略不计[32]，因此可作为输运障壁，将运动系统的相空间划分为具有不同动力性质的子区域[33]，例如波动方程的KAM不变环面、不变流形的双曲不动点及周期性轨迹等[34]。因此，LCSs也被称为是海洋混合的“骨架”[35]。这对研究河口悬浮泥沙输运具有重大意义。

相比传统的基于欧拉观点的海洋中尺度现象诊断方法，拉格朗日分析法可以获得更加细致的，甚至是一些尺度小于速度场空间分辨率的海洋变化特征信息。再者，传统欧拉方法分析流场的瞬时特征量，如涡度、动能、应变率等来识别拟序结构，且很多情况下需要人为定义判别阀值[36]，相比之下，拉格朗日法是基于流场中质点的历史输运信息，而非流场的瞬时特征量，故对流场中的个别异常数据不敏感，具有较好的鲁棒性[37]；且无需人为设定阀值，也不依赖坐标系的选取，故该方法更具客观性，能更加精确地揭示流体质点的混合和输运性质。

通过计算有限时间李雅普诺夫指数(the finite-time Lyapunov exponent, FTLE)来提取流场的LCSs[32,38]。FTLE表征的是初始时刻位于空间中某处的两紧密相邻质点在极短时间τ内收敛或发散的平均指数数率，其数学定义为：

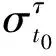
式中：x(t0+τ;t0,x0)表示初始时刻t=t0位于x0的流体质点于t=t0+τ时刻的位置，‖‖表示矩阵谱范数。

考虑二维动力系统，漂流粒子运动方程简化为：

为获取更准确的LCSs信息，需慎重选取计算过程中的三个参数：质点初始距离或FTLE场的网格、积分时间以及积分步长。为使相邻质点初始距离足够小，通常取积分网格精度高于欧拉流场精度，以得到更加细致的流场信息。积分时间的选取遵循两个重要指标：首先，τ应反映流场内一个完整的拉格朗日过程所需的时间。假如一拉格朗日结构所对应的时间尺度为τL，那τ<<τL将妨碍质点沿整个拉格朗日结构的输运[39]，计算结果的LCSs无法得到充分表达。其次，由于流场的空间限制，质点在经过长时间输运后会离开积分区域，过长的积分时间也会导致流场拉格朗日信息的失准。本文中τ控制在关注区域的质点输运至流场边界所需的时间范围内。至于溢出流场的质点则停止计算其FTLE[40-41]。积分步长的选取与流场本身的变化周期有关。对于受潮汐控制的河口地区，其流场变化频繁，拉格朗日时间尺度可短至几十分钟，积分步长相应较短。外海或大洋地区流场变化周期长，其拉格朗日时间尺度可达几天甚至几十天，故积分步长可相应取较长。

通过对流场向前(τ>0)和向后(τ<0)积分计算所得的FTLE为空间标量场，其脊线表征质点局部最大拉伸率或压缩率，分别可近似为排斥型LCSs(稳定流形)和吸引型LCSs(不稳定流形)[32,38]。本文通过四阶龙格库塔积分方案求得质点的历史轨迹信息，并计算其FTLE值来提取流场吸引型LCSs，其具有局部吸附性以及近物质线属性[38]，可作为流体通量的输运障壁。

2 结果与讨论

2.1模式验证

鸡只每隔两周空腹称重，以重复为单位计算体重，按试验分期计算每组平均日增重。每周末下午结算喂料量，按试验分组计算每组耗料量。每两周在每个重复随机抽取4只鸡测定单只体重与胫长。

图3及图4分别为模式水位和流场的验证结果。如图3所示，水位模式结果能较好模拟出珠江河口潮波不规则变化特征。无论是位相还是振幅，4个潮位站的模拟值与实测资料都有着极高的模拟精度，较为真实地重现了珠江河口的潮汐变化过程。本研究取一个潮周期内各连续站点南北方向的流速进行验证，流场验证结果见图4。从总体上看，模拟结果与实测值有良好一致性，各水质点的模拟值无论在空间分布趋势还是量值上都趋近实测值。模拟值与实测值的表层总体均方根误差约为0.2 m/s，底层总体均方根误差则低至0.06 m/s。表层流场模拟精度相对底层较差，这可能与模式中的风场输入有关。由于风对珠江河口表层潮流影响较大，模式中风场不精确可导致表层流速计算偏差较大，但底层流速受影响较小，模拟结果较好。

尽管在流速验证结果上个别站点还存在一定偏差，但从总体验证结果和偏差统计情况可看出，水动力模型能较准确地模拟出观测期间珠江河口潮汐变化规律，具有较高的模拟精度。

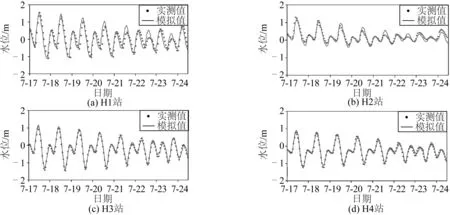
图3 模式计算水位(实线)与实测值(点)的比较Fig. 3 Comparisons between modeled (solid line) and observed water levels at selected stations

图4 模式计算表层(黑实线)和底层(灰线)流速与实测值(点)的比较Fig. 4 Comparisons between modeled calculated (solid line) and observed (dot) current speed on surface (black) and bottom (red) layer

2.2珠江河口LCSs与浊度锋

2.2.1 参数选取

为提取合适的积分参数，对结果LCSs进行敏感性分析。在FTLE场网格精度及积分步长一定的前提下，随着积分时间的增加，FTLE场由总体高值且基本无脊线结构逐渐演变为总体低值且局部出现尖锐突出的脊线结构，见图5(a)～5(d)。这是因为在过短的积分时间里，流场中的大部分质点基本仍处于强拉伸分离状态，且未能完成流场内各个拉格朗日过程的输运，导致流场FTLE平均值相对较高且分布无序，见图5(a)。

在积分时间及积分步长一定的情况下，随着FTLE场精度的增加，LCSs在原有模糊结构的基础上变得愈来愈细致，且表现出多分形特征，见图5(e)～5(h)。原本粗糙精度下的FTLE低值区却隐藏着高精度下的FTLE脊线，而原本低精度下的高值区也可能只是高精度下多条FTLE脊线间的低值区，因此只有在积分场网格精度足够高时，才能充分提取流场的LCSs信息。然而，无穷高的精度并不能得出任意小尺度的流场输运特征，例如当积分场网格精度取0.002°时，可以看出其LCSs并没有比0.005°时提供更小尺度上的信息，且大大增加了计算时间，这主要是由给定流场的拉格朗日输运信息决定的。

不同积分步长对流场LCSs的影响如图5(i)～5(l)所示。随着步长的减小，所得到的LCSs越来越清晰。这是因为对于流场变化频繁的珠江河口，其拉格朗日时间尺度大多在几十分钟至几个小时之间，如若步长取得过大，则会忽略流场一些时间尺度较小的输运信息，导致提取的LCSs失真，见图5(i)、5(j)。

综合考虑以上情况，本文LCSs积分时间取7天，积分网格精度取0.006°，积分步长取0.02天，即保证了计算效率，又足以揭示流场所有时间尺度的LCSs信息。

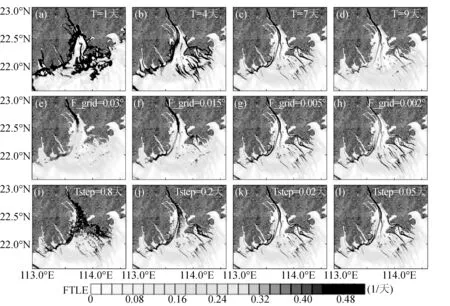
图5 分别取不同积分参数所得的LCSs结果Fig. 5 Maps of LCSs with different integration parameters in the Pearl River Estuary

2.2.2 珠江河口LCSs

受河口内零落分布的岛礁及复杂地形边界的影响，珠江河口水动力及其LCSs呈现复杂的时空变化，见图6。珠江河口的潮流以往复流为主，在转流期间潮流呈逆时针方向旋转，其LCSs主要可分为三种类型：体现口门外径潮流动力差异型LCSs、表征伶仃洋东西部水动力差异的中部型LCSs以及河口东部岬角和岛屿附近的绕流型LCSs。

珠江河口LCSs的时空分布随涨落潮的强弱而改变,在一个潮周期内变化如下：涨憩时，整个伶仃洋水动力较弱，表层流以弱西向流为主，其主要LCSs呈横向结构，见图6(a)。落潮前期，伶仃洋大部分地区潮流开始下泄，强度较低，加之虎门仍处于涨潮阶段，故此时伶仃洋东部海区水动力较弱，与西滩动力差异较小，动力分界线出现在淇澳岛西北部浅滩及贴近西岸处，见图6(b)。随着落潮强度的增大，虎门下泄的落潮射流逐渐增强了东部落潮水动力，使伶仃洋东西部海区动力差异越来越明显，其动力分界线逐渐东移，落急时刻移至西槽附近形成典型伶仃洋中部型LCSs，见图6(c)～6(d)。此期间西四口门外LCSs变化不大，东部绕流LCSs则逐渐增强。落潮后期至落憩，由于河口整体动力逐渐减弱且存在局地性差异，河口FTLE脊线越显分散，至落憩时受东向潮流影响而转成横向结构，见图6(e)、6(f)。涨潮初期，外海潮流流经大濠岛时分为东西两支继续北上，直至东四口门外，受虎门落潮射流与西北三口门径流阻碍作用而在口门外形成LCSs，见图6(g)、6(h)。此期间珠江河口LCSs分布类型以径潮顶托作用形成的LCSs及岛屿绕流LCSs为主。受地形影响，涨潮中后期，潮流主要沿深槽上溯，东西槽流速大，造就伶仃洋两条较明显FTLE脊线生成，见图6(i)～6(k)。此期间珠江河口主要以伶仃洋中部型LCSs和绕流型LCSs为主。

图6 一个涨落潮期间珠江河口LCSs的变化Fig. 6 Maps of flood-ebb LCSs variation in the Pearl River Estuary

图7 模式结果：四个潮汐特征时刻的流场与其FTLE(单位：1/天)场叠加Fig. 7 Maps of modeled calculated surface flow velocity (m/s,vector) overlay with FTLE field (1/day) at four typical moments

为进一步探讨珠江河口LCSs，本文提取四个珠江河口典型时刻流场及其LCSs信息进行具体分析，见图7。如图所示，无论是涨急还是落急，虎门处皆存在强烈的FTLE脊线，见图7中L1、L2，异于其它所有口门，这与虎门特殊的水动力环境有关。虎门属于潮汐优势型河口，潮差大，径潮流强劲，在基岩夹峙下，虎门上下游(狮子洋和伶仃洋)水面放宽，纳潮量增大，从而发育了罕见的双向不对称射流系统[42]，因此在涨潮和落潮时都存在较大的速度切变而形成FTLE脊线。相比之下，蕉门、洪奇门及横门下泄的径流则相对较弱，加之地形作用，西滩形成动力薄弱带，使之在涨落潮时分别与上溯的涨潮流和虎门下泄的落潮射流交汇，由于较大的水平速度切变而形成伶仃洋中部型LCSs，见图7中L4、L5，在口门处和西滩水域则无明显的FTLE高值区。同时，由于涨急时西北三口门的径流与涨潮流的相互顶托作用，口门外形成缓流区或滞流区，从而产生一条明显的动力分界线，见图7中L3。此外，位于伶仃洋东侧的大濠岛西岸以及深圳湾西侧暗士顿水道处，由于涨急与落急时潮流绕过岬角时产生的射流与周围水体存在较大的水平速度切变，从而形成岬角锋[43-44]，因而皆存在较为明显的FTLE脊线，见图7中L6、L7。珠江河口落潮强度大于涨潮强度，而由图可知落潮时河口FTLE脊线无论是数量上还是量值上皆明显大于涨潮，同时涨落急FTLE背景量值明显大于涨落憩时刻，因此LCSs不仅能够清晰地描绘出具有不同动力性质的水体边界，且具备初步量化功能，反映水动力强弱。

2.2.3 珠江河口LCSs与浊度锋的关系

为真实地展示珠江河口浊度锋的分布形态，本研究分别截取某一涨潮时刻和落潮时刻Landsat7 ETM+真彩色合成的卫星图像，见图8(b)、8(d)，其空间分辨率为30 m，可清楚地呈现珠江河口悬浮泥沙的小尺度分布特征。如卫星图像所示，无论是涨潮还是落潮，珠江河口表层悬浮泥沙总体上呈西北向东南递减的趋势，各口门附近水域为含沙量高值区，浊度锋基本分布在西滩及口门附近水域，且以伶仃洋涨落潮浊度锋尤为明显，其位置和形态随着涨落潮流作用发生显著变化。涨潮时，浊度锋偏西北，邻近东四口门，延伸长度较短，高浊度水体集中分布在贴岸较窄的区域内。落潮时，河口浊度锋明显东移，且范围增大，其始于舢板洲，沿西南顺流而下几十公里，可至九洲列岛附近。通过对比模式结果LCSs，见图8(a)、8(c)，可以看出，无论是涨潮还是落潮，珠江河口主要浊度锋空间分布与其LCSs在地理位置上都存在很好的契合。这种契合关系不仅存在于涨落潮主要浊度锋处，也见于磨刀门、崖门、珠海以及澳门附近水域。由于LCSs表征流场不同动力性质子区域的边界，是流体的输运通道和障壁，这意味着在该处存在最大速度梯度和剪切力梯度，沉积物的水平输运在此受阻滞留或发生沉降，因此珠江河口涨落潮浊度锋的空间分布可以在其LCSs分布中得到解释。

图8 模式结果流场LCS与卫星图像对比Fig. 8 Comparisons between modeled LCS and satellite images

位于伶仃洋西北侧的蕉门、洪奇门和横门是伶仃洋河口泥沙的主要输出源。涨潮时，来自西北三口门的淡水径流与涨潮流在口门外汇合，由于径潮流顶托作用而产生强烈的水平速度与密度梯度而在此处形成LCS，阻碍了径流挟带悬浮泥沙的输运，因此产生浊度锋。落潮时，蕉门、洪奇门和横门的淡水越西滩而来，速度较小，而从北面虎门下泄的冲淡水则相对较咸，且流速较大，两者在西航道附近相汇，由于较大的速度切变和密度梯度形成一道明显的动力分界线，加之受科氏力影响，流路右偏，从而形成一条东北—西南向的浊度锋。此外，由于受潮流控制，河口东部海区悬浮泥沙含量远小于西部，故即使存在LCSs，也很难形成浊度锋，因此在涨落潮时伶仃洋东部岬角锋处并无明显浊度锋的存在。

3 结 语

基于珠江河口水文观测资料和三维水动力模型，利用有限时间李亚普诺夫指数提取分析了不同时刻流场中的LCSs，并结合Landsat7卫星遥感资料，探讨珠江河口拉格朗日拟序结构与浊度锋分布及形成机制之间的关系。结果表明：

河口浊度锋与LCSs在时空上存在很好的契合，LCSs调控了河口浊度锋的位置、形态及变化过程。位于伶仃洋西北侧的蕉门、洪奇门和横门是伶仃洋河口泥沙的主要输出源，落潮时，泥沙随西北三口门的落潮射流注入伶仃洋，而北部虎门下泄的冲淡水强度远大于其它三个口门，因此形成了一条明显的FTLE脊线限制悬沙向东输运，加之受柯氏力的作用，流路右偏，造就了浊度锋形成和分布形态。涨潮时，来自西北三口门的淡水径流与涨潮流在口门外汇合，强烈的水平速度与密度梯度使之产生明显的动力边界，阻绝了径流挟带悬浮泥沙的输运，形成输运障壁而产生浊度锋。LCSs很好地勾画及初步量化了不同动力性质的水体边界，因此可以用来对河口浊度锋的位置、形态及变化特征进行识别和动力解释。

在拥有较真实的河口水动力场情况下，LCSs可以作为揭示河口浊度锋分布和演变规律的一个有力理论工具。相比传统的模式模拟和遥感反演，此方法不仅更具客观性，不受任何天气要素的影响，且不受流场中个别异常数据的影响，具备较好的鲁棒性[45]。特别是近年来出现的一些新观测手段，如高频地波雷达，可以获得高分辨率河口表层流场信息，有利于提取更精细的LCSs信息，为进一步揭示河口浊度锋分布规律，特别是高频变化特征，提供了极大便利。

[1] KIRBY R, PARKER W R. A suspended sediment front in the Severn Estuary[J]. Nature, 1982, 295(5848):396-399.

[2] ORTON P M, KINEKE G C. Comparing calculated and observed vertical suspended-sediment distributions from a Hudson River estuary turbidity maximum[J]. Estuarine, Coastal and Shelf Science, 2001, 52(3): 401-410.

[3] YE F, HUANG X, ZHANG D, et al. Distribution of heavy metals in sediments of the Pearl River Estuary, Southern China: Implications for sources and historical changes[J]. Journal of Environmental Sciences, 2012, 24(4): 579-588.

[4] 王勇智,鞠霞,乔璐璐,等. 夏冬季北黄海水体浊度分布特征研究[J]. 海洋与湖沼, 2014, 45(5): 928-937. (WANG Y Z, JU X, QIAO L L, et al. Water turbidity in the northern Yellow sea in summer and winter[J]. Oceanologia Et Limnologia Sinica, 2014, 45(5): 928-937. (in Chinese))

[5] EISMA D. Flocculation and de-flocculation of suspended matter in estuaries[J]. Netherlands Journal of Sea Research, 1986, 20(2): 183-199.

[6] FESTA J F, HANSEN D V. Turbidity maxima in partially mixed estuaries: a two-dimensional numerical model[J]. Estuarine and Coastal Marine Science, 1978, 7(4): 347-359.

[7] FENG H, COCHRAN J K, HIRSCHBERG D J. 234 Th and 7 Be as tracers for the sources of particles to the turbidity maximum of the Hudson River Estuary[J]. Estuarine, Coastal and Shelf Science, 1999, 49(5): 629-645.

[8] 黄以琛,李炎,邵浩,等. 北部湾夏冬季海表温度, 叶绿素和浊度的分布特征及调控因素[J]. 厦门大学学报:自然科学版, 2008, 47(6): 856-863. (HUANG Y C, LI Y, SHAO H, et al. Seasonal variations of sea surface temperature, chlorophyll-a and turbidity in Beibu Gulf, MODIS imagery study[J]. Journal of Xiamen University, Natual Science, 2008, 47(6): 856-863. (in Chinese))

[9] 刘汾汾, 陈楚群, 唐世林, 等. 基于现场光谱数据的珠江口MERIS悬浮泥沙分段算法[J]. 热带海洋学报, 2009(1): 9-14. (LIU F F, CHEN C Q, TANG S L, et al. A piecewise algorithm for retrieval of suspended sediment concentration based on in situ spectral data by MERIS in Zhujiang River estuary[J]. Journal of Tropical Oceanography, 2009(1): 9-14. (in Chinese))

[10] ZHANG M, TANG J, DONG Q, et al. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery[J]. Remote Sensing of Environment, 2010, 114(2): 392-403.

[11] WARRICK J A, MERTES L A K, SIEGEL D A, et al. Estimating suspended sediment concentrations in turbid coastal waters of the Santa Barbara Channel with SeaWiFS[J]. International Journal of Remote Sensing, 2004, 25(10): 1 995-2 002.

[12] MIN J E, RYU J H, LEE S, et al. Monitoring of suspended sediment variation using Landsat and MODIS in the Saemangeum coastal area of Korea[J]. Marine Pollution Bulletin, 2012, 64: 382-390.

[13] HALLER G, YUAN G. Lagrangian coherent structures and mixing in two-dimensional turbulence[J]. Physica D: Nonlinear Phenomena, 2000, 147(3): 352-370.

[14] WIGGINS S. The dynamical systems approach to Lagrangian transport in oceanic flows[J]. Annu. Rev. Fluid Mech., 2005, 37: 295-328.

[15] BRANICKI M, WIGGINS S. Finite-time Lagrangian transport analysis: stable and unstable manifolds of hyperbolic trajectories and finite-time Lyapunov exponents[J]. Nonlinear Processes in Geophysics, 2009, 17(1):1-36.

[16] D'OVIDIO F, FERNNDEZ V, HERNNDEZ-GARCA E, et al. Mixing structures in the Mediterranean Sea from finite-size Lyapunov exponents[J]. Geophysical Research Letters, 2004, 31(17):345-359.

[17] RYPINA I I, PRATT L J, PULLEN J, et al. Chaotic advection in an archipelago[J]. Journal of Physical Oceanography, 2010, 40(9): 1 988-2 006.

[18] LEKIEN F, COULLIETTE C, MARIANO A J, et al. Pollution release tied to invariant manifolds: A case study for the coast of Florida[J]. Random House, 1987, 210(1-2):1-20.

[19] COULLIETTE C, LEKIEN F, PADUAN J D, et al. Optimal pollution mitigation in Monterey Bay based on coastal radar data and nonlinear dynamics[J]. Environmental Science & Technology, 2007, 41(18): 6 562-6 572.

[20] LEHAHN Y, D'OVIDIO F, LÉVY M, et al. Stirring of the northeast Atlantic spring bloom: A Lagrangian analysis based on multisatellite data[J]. Journal of Geophysical Research, 2007, 112(112):207-220.

[21] OLASCOAGA M J. Isolation on the West Florida Shelf with implications for red tides and pollutant dispersal in the Gulf of Mexico[J]. Nonlinear Processes in Geophysics, 2010, 17(6):685-696.

[22] HUHN F, VON KAMEKE A, ALLEN-PERKINS S, et al. Horizontal Lagrangian transport in a tidal-driven estuary—Transport barriers attached to prominent coastal boundaries[J]. Continental Shelf Research, 2012, 39: 1-13.

[23] 黄高龙,韦惺,詹海刚. 吕宋海峡浮标轨迹的拉格朗日拟序结构分析[J]. 热带海洋学报, 2015, 34(1): 15-22. (HUANG G L, WEI X, ZHAN H G. Lagrangian analysis of drifter trajectories near the Luzon Strait[J]. Journal of Tropical Oceanography, 2015, 34(1): 15-22. (in Chinese))

[24] KAI E T, ROSSI V, SUDRE J, et al. Top marine predators track Lagrangian coherent structures[J]. Proceedings of the National Academy of Sciences, 2009, 106(20): 8 245-8 250.

[25] COTTÉ C, D'OVIDIO F, CHAIGNEAU A, et al. Scale-dependent interactions of Mediterranean whales with marine dynamics [J]. Limnology and Oceanography, 2011, 56(1): 219-232.

[26] 吴超羽, 包芸, 任杰, 等. 珠江三角洲及河网形成演变的数值模拟和地貌动力学分析:距今6 000～2 500 a[J]. 海洋学报, 2006, 24(4): 64-80. (WU C Y, BAO Y, REN J, et al. A numerical simulation and mophodynamic analysis on the evolution of the Zhujiang River Delta in China: 6 000～2 500 a BP[J]. Acta Oceanologica Sinica, 2006, 24(4): 64-80. (in Chinese))

[27] 宋定昌, 阮孤松. 珠江八大口门潮汐潮量的初步分析[M]//珠江口海岸带和海涂资源综合调查研究文集(四). 广州：广东科技出版社, 1986: 62-71. (SONG D C,YUAN G S. A preliminary analysis of tidal tidal volume in the eight mouth of the Pearl River[M]//The Pearl River Estuary Coastal Zone and Coastal Resources Comprehensive Survey. Guangzhou: Guangdong Science and Technology Press, 1986: 62-71.(in Chinese))

[28] CHEN J C, HEINKE G W, ZHOU M J. The Pearl River estuary pollution project (PREPP)[J]. Continental Shelf Research, 2004, 24(16): 1 739-1 744.

[29] EDELVANG K, LUND-HANSEN L C, CHRISTIANSEN C, et al. Modelling of suspended matter transport from the Oder River[J]. Journal of Coastal Research, 2002: 62-74.

[30] LUMBORG U. Modelling the deposition, erosion, and flux of cohesive sediment through Øresund[J]. Journal of Marine Systems, 2005, 56(1): 179-193.

[31] WEI X, NI P, ZHAN H. Monitoring cooling water discharge using Lagrangian coherent structures: A case study in Daya Bay, China[J]. Marine Pollution Bulletin, 2013, 75(1): 105-113.

[32] SHADDEN S C, LEKIEN F, MARSDEN J E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows[J].Physica D Nonlinear Phenomena, 2005, 212(3-4):271-304.

[33] PEACOCK T, DABIRI J. Introduction to focus issue: Lagrangian coherent structures[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2010, 20(1): 017501.

[34] YUAN G C, PRATT L J, JONES C K R T. Cross-jet Lagrangian transport and mixing in a 2 1/2-layer model[J]. J. Phys. Oceanogr., 2004, 34(9): 1 991-2 005.

[35] MATHUR M, HALLER G, PEACOCK T, et al. Uncovering the Lagrangian skeleton of turbulence[J]. Physical Review Letters, 2007, 98(14):4 055-4 055.

[36] WANG G H, SU J L, CHU P C. Mesoscale eddies in the South China Sea observed with altimeter data[J]. Physical Review Letters, 2003, 30 (21): 10.1029/2003GL018532.

[37] HARRISON C, GLATZMAIER G. Lagrangian coherent structures in the California Current System-sensitivities and limitations[J]. Geophys. Astrophys. Fluid Dyn., 2010: 1-23.

[38] HALLER G. Lagrangian structures and the rate of strain in a partition of two-dimensional turbulence[J]. Physics of Fluids (1994-present), 2001, 13(11): 3 365-3 385.

[39] BRANICKI M, MALEK-MADANI R. Lagrangian structure of flows in the Chesapeake Bay: challenges and perspectives on the analysis of estuarine flows[J]. Nonlinear Processes in Geophysics, 2010, 17(2): 149-168.

[40] ABRAHAM E R, BOWEN M M. Chaotic stirring by a mesoscale surface-ocean flow[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2002, 12(2): 373-381.

[41] HUHN F, VON KAMEKE A, ALLEN-PERKINS S, et al. Horizontal Lagrangian transport in a tidal-driven estuary—Transport barriers attached to prominent coastal boundaries[J]. Continental Shelf Research, 2012, 39: 1-13.

[42] 任杰, 吴超羽, 包芸. 珠江虎门口动力结构研究[J]. 中山大学学报: 自然科学版, 2006, 45(3): 105-109. (REN J, WU C Y, BAO Y, et al. Dynamic structure of humen esturay of the Pearl River[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2006, 45(3): 105-109. (in Chinese))

[43] BOWMAN M J, IVERSON R L. Estuarine and plume fronts[M]//Oceanic Fronts in Coastal Processes. 1978: 87-104.

[44] 应秩甫. 珠江口伶仃洋锋的类别及其对沉积的影响[J]. 热带海洋, 1994, 13(2): 25-32.(YING Z F. The frontal classification and its influence on sedimentation in Lingdingyang, Zhujiang River estuary[J]. Tropic Oceanology, 1994, 13(2): 25-32. (in Chinese))

Lagrangian coherent structures in the Pearl River Estuary and its use in identifying turbidity fronts

ZHAN Weikang1,2，WEI Xing1，YE Haibin1，ZHAN Haigang1

(1. State Key Laboratory of Tropical Oceanography, Guangzhou 510301, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)

1005-9865(2017)02-0039-11

P751

A

10.16483/j.issn.1005-9865.2017.02.007

2016-06-01

广州市科技计划项目(201607020042)；热带海洋环境国家重点实验室自主研究项目(LTOZZ1503)

詹伟康(1991-),男,广东潮州人,主要从事河口水沙动力学的研究。

詹海刚。E-mail：hgzhan@scsio.ac.cn