双整体式止屈器结构性能研究及优化设计

吴梦宁, 余建星, 孙震洲, 段晶辉

(1. 天津大学 水利工程仿真与安全国家重点试验室，天津 300354; 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

双整体式止屈器结构性能研究及优化设计

吴梦宁1, 2, 余建星1, 2, 孙震洲1, 2, 段晶辉1, 2

(1. 天津大学 水利工程仿真与安全国家重点试验室，天津 300354; 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

建立了双整体式止屈器结构的三维有限元模型，模拟其在外部静水压力作用下的屈曲穿越过程，总结不同穿越破坏模式的产生条件及机理。对影响穿越破坏压力的主要参数进行敏感性分析，结果表明止屈器布置间距、两个止屈器的几何尺寸均会对整体止屈性能产生影响。在拟合的双整体式止屈器效率公式的基础上，依据非线性有约束优化理论，分别采用经典算法和智能遗传算法确定模型最优解，提出了一种兼顾结构重量与止屈性能的最优双整体式止屈器结构型式；并经计算分析，验证了该方法的可靠性和适应性。

双整体式止屈器；穿越模式；拟合公式；结构设计

Abstract: A finite element(FE) model was developed to simulate the crossover of the double-integral buckle arrestors(DIBA) under the ambient externa hydrostatic pressure. In this study, the condition and mechanism of different crossover modes during the process of arresting were summarized. Then, the impact based on series of structure parameters on the DIBA’s crossover pressure was studied. The results indicated that the arresting performance of the model could be affected by many factors, such as, the space between arrestors and the geometrical dimensions of each arrestor. After analyzing the result of sensitivity, a fitting formula on DIBA’s arresting efficiency was put forward in the paper. At last, the structure optimization model of DIBA was established, both arithmetic and genetic algorithms are introduced to solve the problem, which is based on the constrained nonlinear programming theory. The result shows that the optimal double-integral buckle arrestor is an advanced buckling arrest measure, with excellent arresting performance and lower structural weight. And the measure has been verified to have good performance in reliability and adaptability through calculation and analyse.

Keywords: double-integral buckle arrestors; crossover modes; fitting formulas; structural design

近年来，随着海洋油气资源勘探开发的重点开始转向深水及超深水区域，巨大外部静水压力及恶劣复杂的作业环境所带来的海底管道屈曲失效问题愈加严重。相较于长距离铺设厚壁管道在结构重量、铺设难度及维修成本等方面的弊端，沿海底管道长度方向间隔布置止屈器的方法优势明显。从20世纪80年代开始，各类止屈器就已经成为海底管道止屈措施研究的热点，但目前还处于理论探讨和室内试验阶段，没有投入实际应用。研究证明，整体式止屈器以其优异的止屈性能，是各类止屈器中最适用于(超)深水海底管道铺设中的止屈装置[1-2]。整体式止屈器是焊接在管道指定位置处的厚壁圆环，通过局部加强管道刚度，从而防止屈曲沿管道轴向传播的装置。由于海底管道的铺设距离逐年增加，若采用整体式止屈器抑制屈曲传播的方法，势必需沿管道布置多个。对于单个整体式止屈器，其止屈性能受多重因素影响，主要包括管道径厚比[3]、止屈器长度及厚度[4-6]、材料特性[3， 7-8]、外部环境[9-11]等。相比之下，多个整体式止屈器共同作用的情况就更加复杂，需在此基础上考虑不同布置间距对整体止屈性能的影响效果、不同尺寸止屈器间搭配所产生的相互作用等问题。近几年来，对整体式止屈器的研究，总体上局限于单个止屈器的设计标准及形式方面[12-14]，但仅凭借单个止屈器的试验研究结果，不足以有效指导其在实际工程中的应用。美国奥斯汀大学曾沿管长布置两个整体式止屈器进行试验研究[4-5]，但其目的在于降低试验次数，提高试验效率，因此在试验中将两个止屈器远距离布置，使二者间不足以相互影响。李旭等[15]在对止屈器设计方法的研究中，仅基于管材采办费用确定止屈器间距，并未考虑止屈器间的力学性能。可见，对多个止屈器联合作用下止屈效果的研究，目前还处于空白阶段，对其研究具有极其重要的工程意义。另外，在结构分析方法方面，相较于传统设计方法需多次迭代、重复分析，价格昂贵等缺点，遗传算法、神经网络等智能优化法于20世纪80年代相继提出，该类方法最优解的获得不需要目标函数和约束条件的导数信息，为复杂工程的优化设计提供了新的思路和方法，近年来已成功应用于实际工程优化设计中。

本文以双整体式止屈器为研究对象，通过数值仿真技术完成对不同结构型式的双止屈器在外部静水压力作用下的屈曲穿越过程模拟，研究止屈性能随各设计参数的变化趋势。在此基础上，建立双止屈器结构的优化设计模型，通过结构参数优化设计，得到满足止屈性能、制造成本等要求的最优结构。

1 屈曲穿越双整体式止屈器有限元模型

1.1模型建立

首先建立具有0.2%端部椭圆度缺陷的管道带双止屈器的整体几何模型。根据外部静水压力作用下模型压溃变形呈对称的特点，将x=0、y=0、z=0三个平面均设置为对称面，仅建立1/4模型以进行简化。以止屈器为分界，将模型分为上游管段LU(包括屈曲诱发段LUO、纯圆段LU1与LUc)、第一止屈器段(LAR1与两侧过渡段LT1)、中间管段LG、第二止屈器段(LAR2与两侧过渡段LT2)及下游管段LD(包括LD1和LDc)五部分。具体几何模型如图1所示。

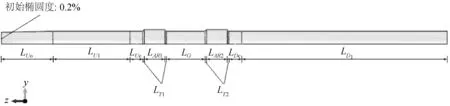
图1 双整体式止屈器几何模型Fig. 1 Model of double-integral buckle arrestors

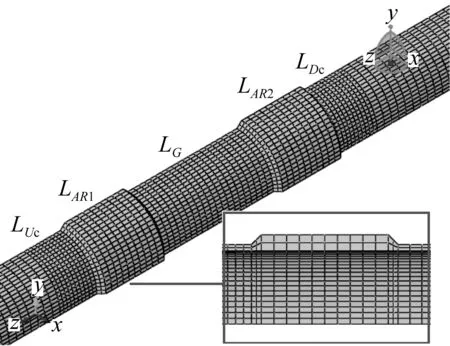
图2 双止屈器附近的网格划分Fig. 2 Meshes near double-integral buckle arrestors

管道及止屈器模型均采用8节点六面体线性非协调模式单元C3D8I。为模拟后屈曲阶段管壁的接触效应，引入两个分别位于XZ平面与YZ平面的解析刚性面作为主面，各自与作为从面的管道内壁面构成接触对，并设置刚体参考点施加六个自由度全约束。在模型外部区域建立流体加载舱，采用流体质量加载方法，通过手工修改原始模型的INP代码施加外部静水压力。网格划分上，沿管道壁厚方向划分2个单元、圆周方向划分24个单元，沿轴线方向分成不同长度的区段，根据不同区段的长度及所关心的重要性决定划分单元的个数，如在双止屈器两侧设置网格加密区以保证模拟效果，如图2所示。

1.2模拟结果

以外径51 mm、壁厚2 mm的管件，配两个长度40.8 mm、壁厚4.4 mm的整体式止屈器所组成的双止屈器模型进行止屈建模计算，两个止屈器的间距取为4.0倍管道外径，材质均为SS304钢材。通过ABAQUS软件进行双止屈器的屈曲穿越模拟，输出每一个载荷子步的静水流体压力和静水流体腔体体积，通过换算得到模型所受外压和流体腔内体积的压缩量，绘出准静态加载压力曲线，如图3所示。

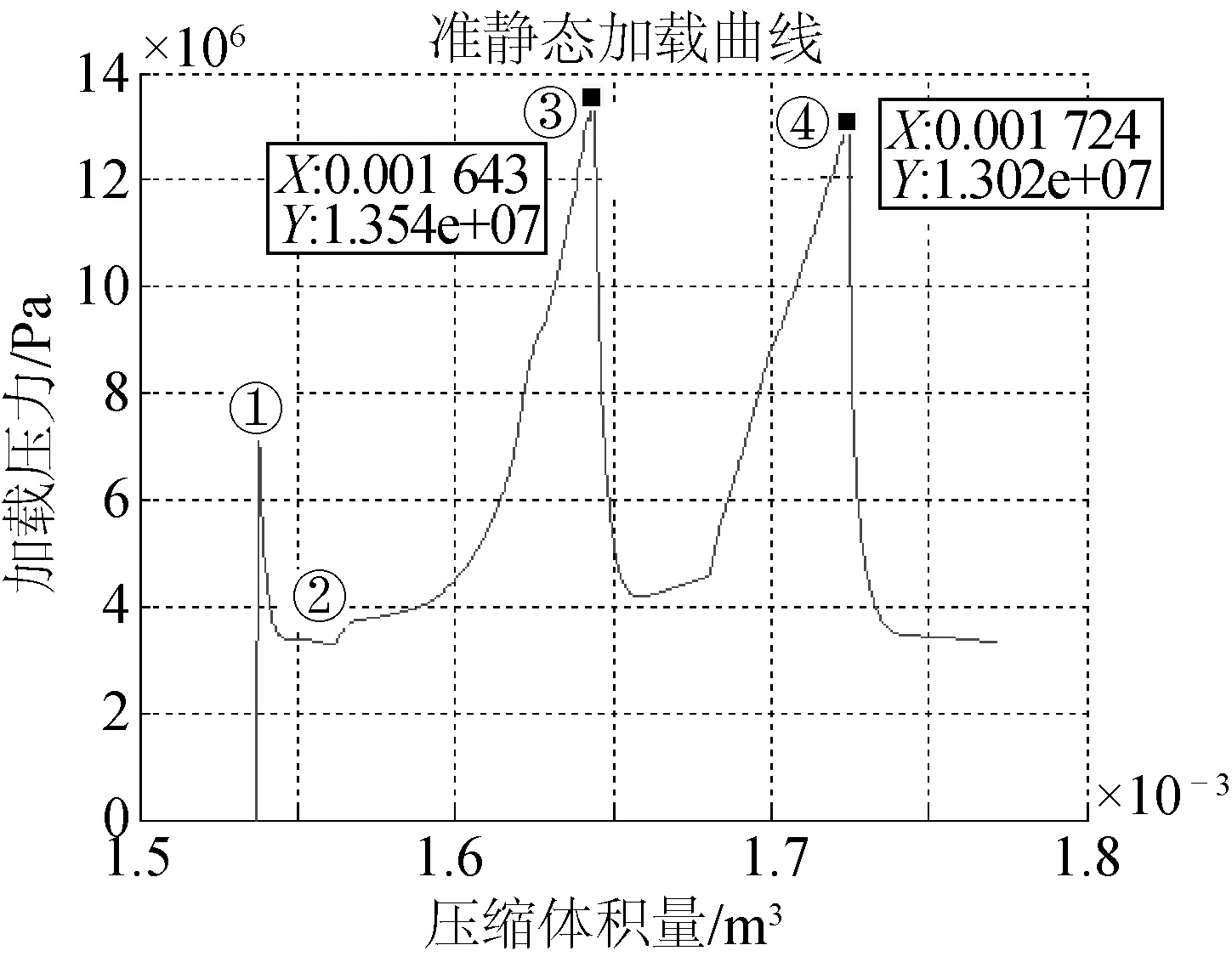
图3 准静态加载压力曲线Fig. 3 Quasi-static pressure curve of double-integral buckle arrestors

图4 模型屈曲穿越变形过程云图Fig. 4 Mises stress nephogram of buckling and crossover

由图可知，双止屈器屈曲穿越过程与单止屈器类似。加载过程中压力上升至①处(约7.2 MPa)时管道局部缺陷处开始压溃，压力迅速下降，直至②处管道内壁首次相互接触(约3.3 MPa)时压力回升，此时压溃变形停止，屈曲开始向下游传播。随后由于第一个止屈器对管道的强化作用，压力继续上升直到屈曲传播至该止屈器。该过程的压力峰值③即第一个止屈器的穿越破坏压力为13.54 MPa。当屈曲穿越第一个止屈器后，管道外压由于中间管道的压溃会迅速下降，随屈曲传播逐渐接近第二个止屈器又逐步上升，达到的第二个压力峰值④即第二个止屈器的穿越破坏压力，为13.02 MPa。模型屈曲穿越过程的应力云图如图4所示。

1.3穿越破坏模式

双整体式止屈器结构在屈曲穿越过程中，会呈现出较单止屈器更为多样的穿越破坏模式。为避免产生歧义，以“未穿越”、“0°穿越”、“90°穿越”对其中每一止屈器的穿越模式进行描述。具体来说，“未穿越模式”主要针对第一个止屈器连同中间管段均不会压溃而保持完整性的情况，此时称第一个止屈器发生“未穿越模式”；“0°穿越模式”表示止屈器下游管段压溃方向与上游屈曲传播方向相同；“90°穿越”表示止屈器下游管段压溃方向与上游屈曲传播方向呈90°。

近间距双止屈器结构在外部静水压力下，会出现第一个止屈器不穿越、中间管段不压溃的现象，这种穿越破坏模式统称为单穿越模式。根据两止屈器相对刚度大小及间距的不同，细分为“未穿越-90°穿越”模式和“未穿越-0°穿越”模式两种。当止屈器布置间距较近时，两止屈器连同中间管段可看作整体、共同抵抗屈曲传播，下游管段由于反向椭圆度的作用发生90°穿越，如图5(a)所示。当止屈器布置间距扩大到需考虑两止屈器对中间管段的影响效果、且第一个止屈器刚度较大时，屈曲波形仍可被第一个止屈器有效阻止，中间管段首先产生由上游屈曲带来的反向椭圆度，随后使下游管段产生“反向-反向”椭圆度，下游管段的变形方向由该椭圆度方向决定，产生了与原屈曲方向一致的压溃，同时双止屈器结构产生“未穿越-0°穿越”模式，如图5(b)所示。

远间距双止屈器结构在外部静水压力下会出现两个止屈器各自发生穿越、中间管段被压溃的现象，这种穿越破坏模式统称为双穿越模式。具体穿越模式与其中包含的两个止屈器刚度均相关，表现为整体穿越模式与其中止屈器单个作用时的穿越模式对应，根据不同刚度组合的双止屈器模型分为“0°-0°穿越”模式、“0°-90°穿越”模式、“90°-0°穿越”模式和“90°-90°穿越”模式四种。将不同穿越模式的发生条件总结至表1，四种穿越模式分别如图6(a)～6(d)所示。

图5 单穿越模式Fig. 5 Single corssover mode

双止屈器穿越模式单个止屈器单独作用时穿越模式第一个止屈器第二个止屈器0°-0°平行平行0°-90°平行正交90°-0°正交平行90°-90°正交正交

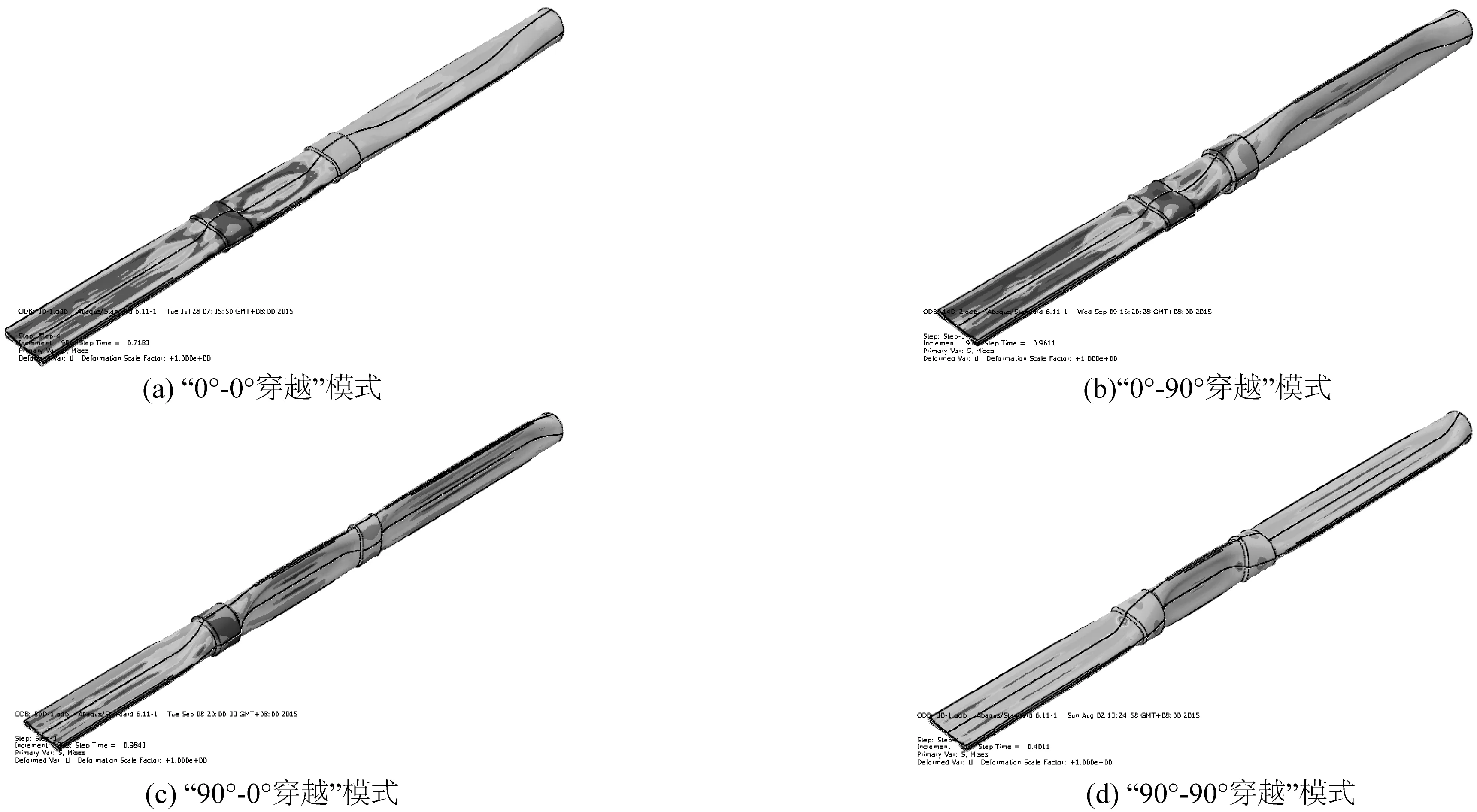
图6 双穿越模式Fig. 6 Double-crossover mode

2 双整体式止屈器结构性能分析

双整体式止屈器止屈效果的评价，以求得整体结构的穿越破坏压力为核心目标。主要关注两个止屈器的布置间距，第一个止屈器的壁厚、长度，第二个止屈器的壁厚、长度等参数对结构穿越压力的影响效果。分析中参数D表示管道外径，t表示管道壁厚，La1表示第一个止屈器长度，h1表示第一个止屈器厚度，La2表示第二个止屈器长度，h2表示第二个止屈器厚度，L表示两止屈器布置间距。

2.1穿越破坏压力对止屈器布置间距的敏感性

不同刚度止屈器所组成的双止屈器模型，屈曲穿越机理有明显区别，因此以止屈器厚度作为刚度评价指标，对双止屈器模型进行分类，研究不同刚度组合双止屈器模型中穿越压力对间距的敏感性。

模型中选用厚度h为3.0t和2.2t的两种止屈器，分别定义为“厚”止屈器和“薄”止屈器，长度La固定为0.8D，以两个止屈器之间的距离L作为变化参数，得到不同模型穿越破坏压力随止屈器布置间距的敏感性曲线，如图7所示。图中红色的水平线为相同材料及几何尺寸的单止屈器穿越破坏压力。“单穿越压力”曲线对应单穿越模式中整体结构穿越压力结果，“第一、第二穿越压力”曲线分别对应双穿越模式中的第一个、第二个止屈器穿越破坏压力结果。

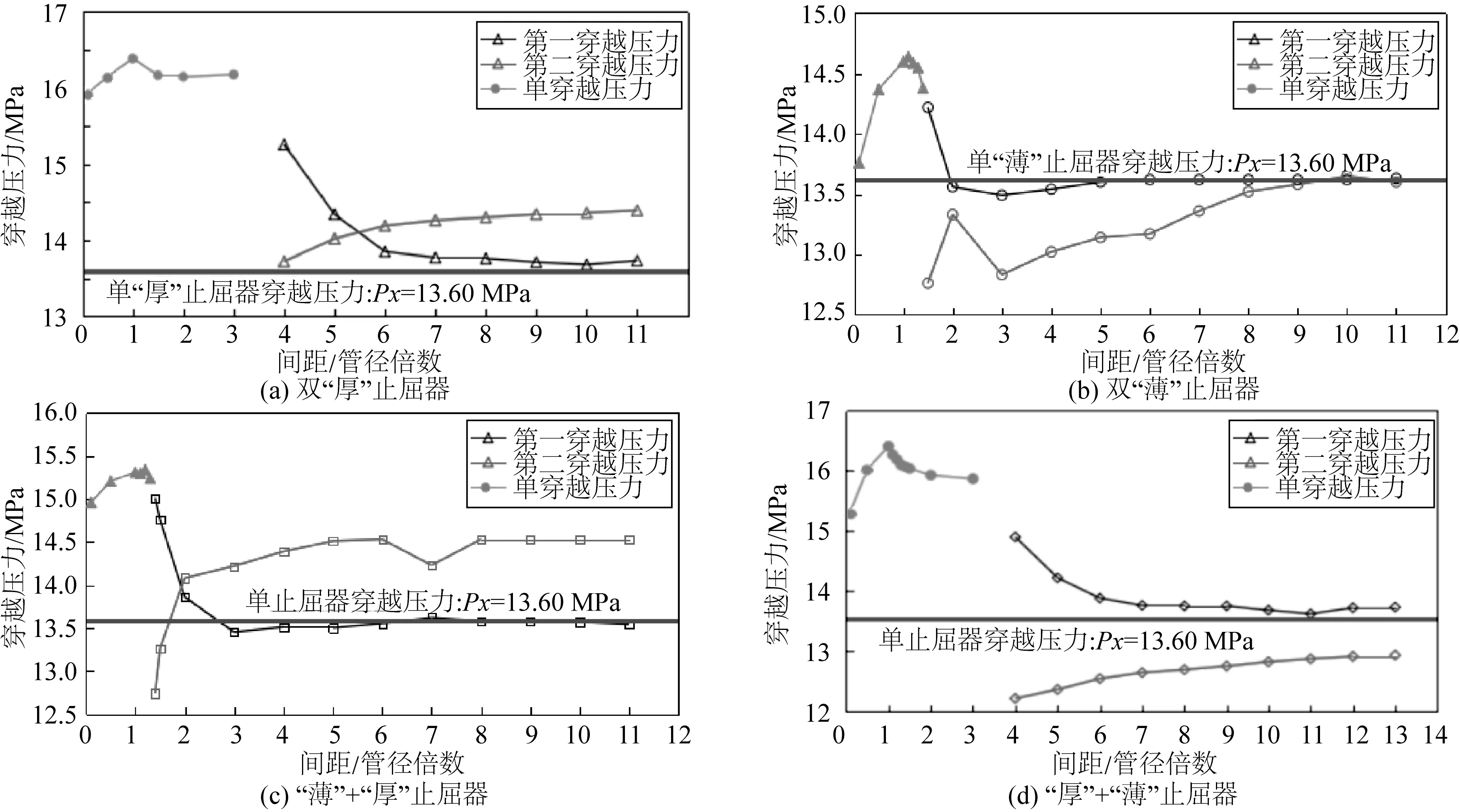
图7 穿越破坏压力的间距敏感性曲线Fig. 7 Crossover pressure plotted against the space between arrestors

由敏感性曲线可知，止屈器布置间距对穿越破坏压力的影响作用显著：

1)随止屈器布置间距的增加，各双止屈器模型均表现出从单穿越模式到双穿越模式的变化趋势；

2)单穿越模式中，穿越破坏压力随布置间距的增加先升高后降低，穿越破坏压力水平总体较高；双穿越模式中，第一穿越压力随布置间距的增加先大幅降低、后基本稳定在对应的单止屈器穿越压力水平，第二穿越压力随布置间距的增加先小幅提升、后基本稳定不变，稳定值根据第二止屈器刚度而有所区别。

综上，近间距双止屈器结构适用性更高。一方面，近间距布置能保证中间管段的结构完整性，且整体结构的止屈效果显著优于单个止屈器及间距较远双止屈器；另一方面，中间管段越短，整个双止屈器结构的用料越少，在经济方面具有明显的优势。

2.2穿越破坏压力对止屈器厚度的敏感性

鉴于近间距双止屈器模型兼具止屈效率与结构重量上的优势，针对间距为3.0D以内的双止屈器模型，进行单止屈器厚度对穿越破坏压力的敏感性计算。

图8(a)为固定两个止屈器长度均为0.80D，第二个止屈器厚度h2为1.8t，模型在不同布置间距下，穿越破坏压力随第一个止屈器厚度的变化趋势。图8(b)中止屈器长度及布置间距与上述相同，固定第一个止屈器厚度h1为3.0t，仅改变第二个止屈器厚度进行计算。两图中红色水平线代表管道的压溃压力，不同颜色曲线代表不同布置间距结果。另外，为比较两厚度对双止屈器模型穿越破坏压力影响效果的差异，计算固定间距(L=1.0D)下穿越破坏压力随单止屈器厚度的变化趋势，如图8(c)所示。

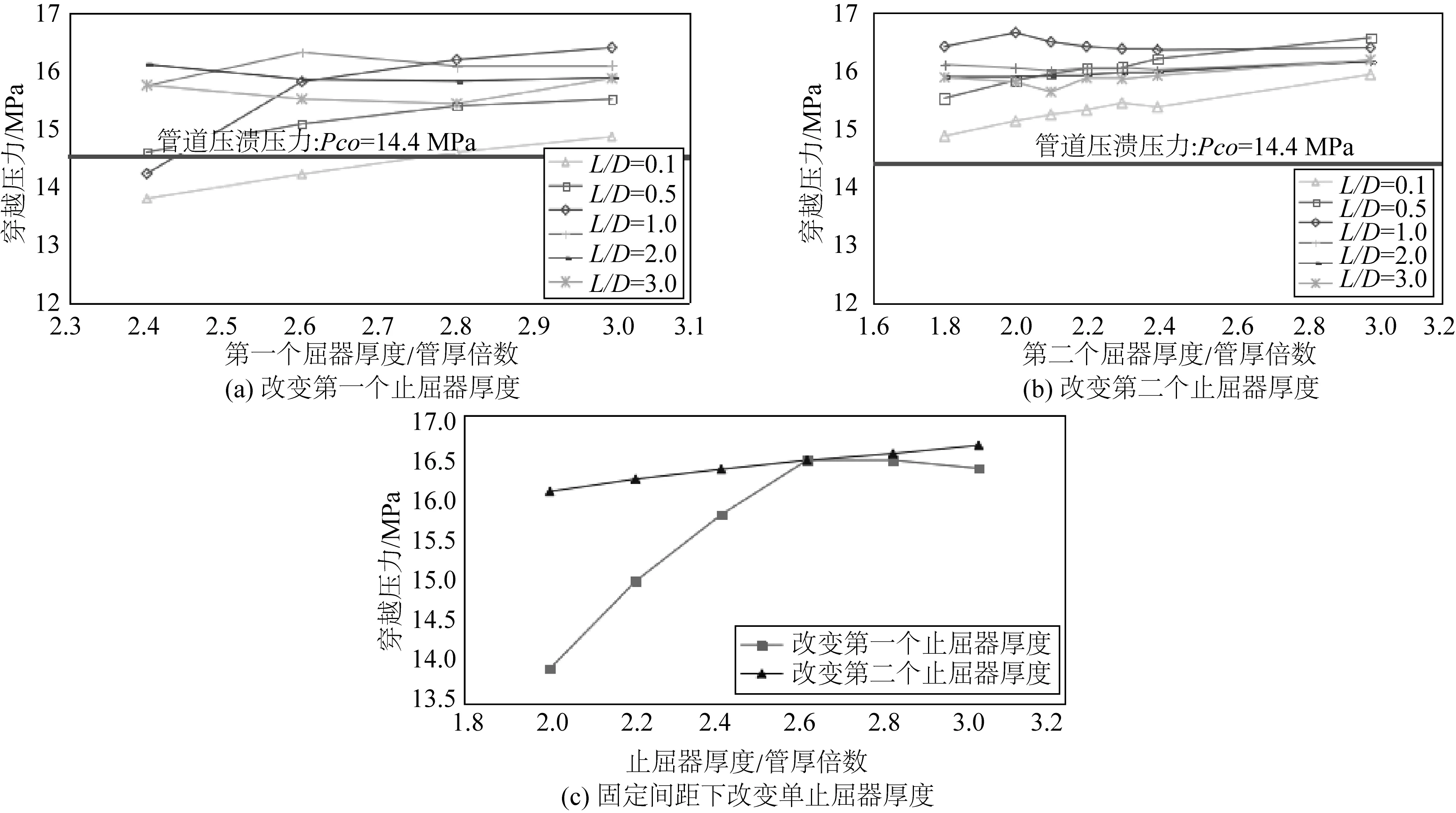
图8 穿越破坏压力的止屈器厚度敏感性曲线Fig. 8 Crossover pressure plotted against thickness of arrestor

由敏感性曲线可知：

1)止屈器间距在1.0D范围内，穿越破坏压力随每一止屈器厚度的增加而逐渐增加；当间距扩大到1.0D至3.0D范围内，穿越过程复杂，穿越压力的大小要考虑反向椭圆度等影响因素，与每一止屈器厚度并无明显关系，但各组结果相差不大，此时止屈器厚度对模型止屈性能的影响效果降低。

2)固定布置间距下，穿越破坏压力对第一个止屈器厚度的敏感性更强，随第一个止屈器厚度的增加显著提升，随第二个止屈器厚度的增加而变化不明显。

综上，第一个止屈器厚度是整体结构穿越破坏压力的强敏感性因素，第二个止屈器厚度是弱敏感性因素。实际设计中，可适当减薄第二个止屈器，以降低整体结构的重量，减少安装难度及成本。

2.3穿越破坏压力对止屈器长度的敏感性

固定第一个止屈器厚度为1.8t，第二个止屈器厚度为3.0t，止屈器原始长度均为0.80D，分别改变单个止屈器的长度，研究近间距双止屈器模型在不同布置间距下，穿越破坏压力随单止屈器长度的变化趋势，结果如图9(a)、9(b)所示。同时，建立固定间距L为1.0D的双“薄”止屈器及双“厚”止屈器模型，仅改变单一止屈器长度，对比分析两止屈器长度对穿越破坏压力的影响效果，结果如图9(c)、9(d)所示。图9(c)中蓝色曲线在0.4D、0.5D的不连续点，代表模型在该几何尺寸下发生了双穿越模式。

由敏感性曲线可知：

与止屈器厚度的影响效果类似，间距在1.0D范围内穿越破坏压力随单止屈器长度的增加而近似线性增加，间距在1.0D至 3.0D范围内长度的影响效果降低。

固定间距下，第一个止屈器的长度对双止屈器模型的止屈性能影响更为明显，但影响效果并不具有很好的规律性，需针对具体情况分析；第二个止屈器长度对双止屈器模型止屈性能的影响总体不大。

综上，与第二个止屈器长度相比，双止屈器结构穿越破坏压力对第一个止屈器长度的敏感性更强。在第一个止屈器长度较短情况下，厚度较薄时会造成整体刚度不够而使两个止屈器均发生穿越；厚度较厚时可能使穿越模式发生变化同时穿越压力发生波动。因此，在设计中可适当加长第一个止屈器，以保证双止屈器结构的止屈性能稳定性。

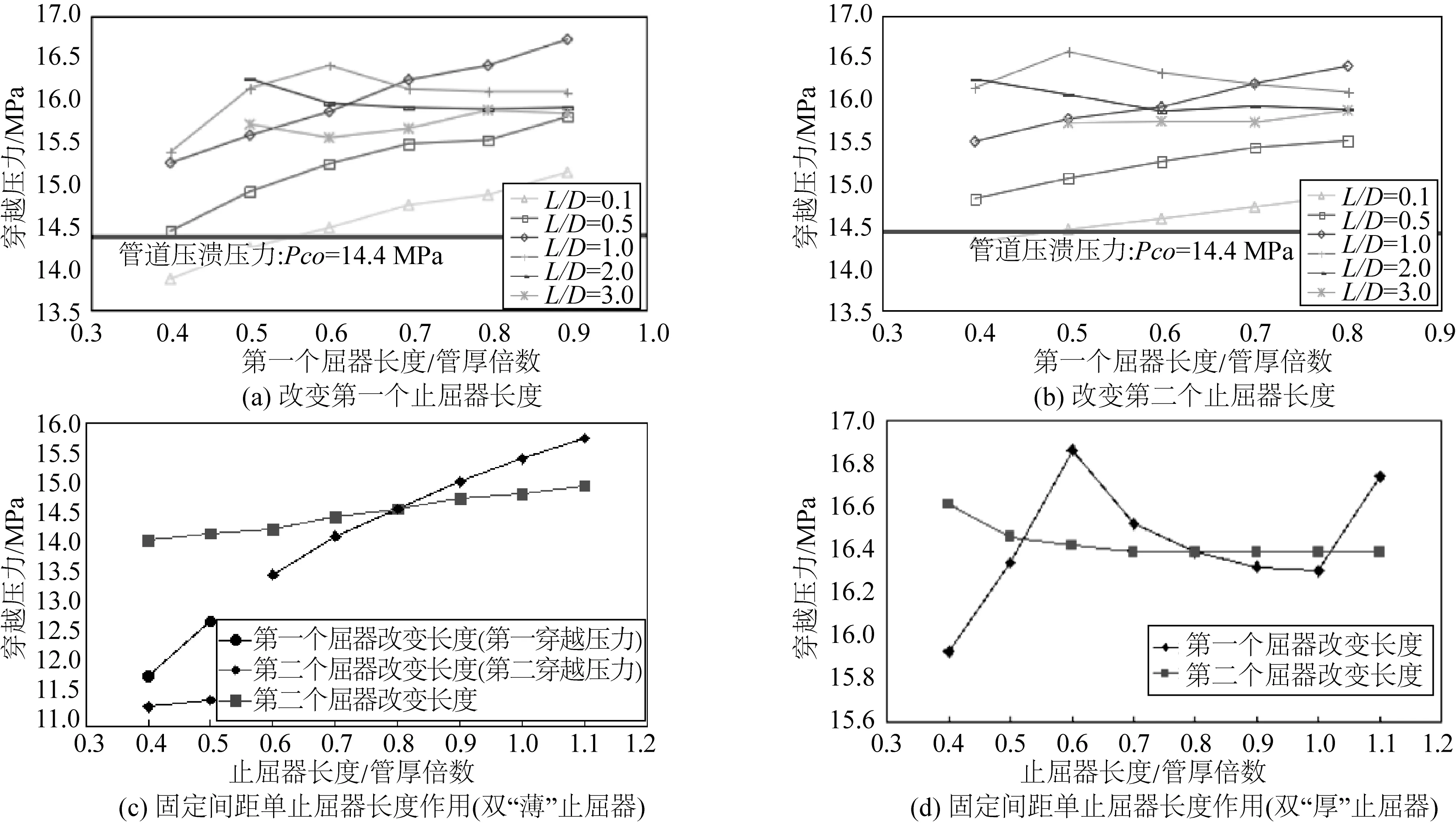
图9 穿越破坏压力的止屈器长度敏感性曲线Fig. 9 Crossover pressure plotted against length of arrestor

3 双整体式止屈器结构优化设计

在双整体式止屈器的设计过程中，理论上存在一个最佳尺寸。结构尺寸过大，会造成材料的浪费；但尺寸过小又起不到抑制屈曲传播的目的，最佳结构需在止屈效率与结构重量间达到平衡。

3.1数学模型

3.1.1 设计变量

以无量纲参数止屈器间距(L/D)、第一个止屈器长度(La1/D)、第一个止屈器厚度(h1/t)、第二个止屈器长度(La2/D)、第二个止屈器厚度(h2/t)作为设计变量，以式(1)所示的向量X代表双整体式止屈器的设计方案。

3.1.2 目标函数

由于设计变量仅有尺寸参数，运用结构最小重量的设计方法，将双整体式止屈器结构重量最低作为目标函数，如式(2)所示。式中一、二项分别为两个止屈器的重量，第三项为中间管段的重量。

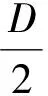
3.1.3 约束条件

由于止屈器最重要的功能是抑制屈曲形式的传播，以止屈效率约束其结构设计。止屈效率η[16]计算公式如式(3)所示。在单止屈器的设计中，一般认为止屈效率达到78%即为高效率止屈器[17]。为体现双整体式止屈器结构在止屈性能上的优势，结构设计中规定止屈效率不低于1.0，即如式(4)：

鉴于双整体式止屈器的止屈效率没有现有理论及规范参考，利用有限元计算结果进行止屈效率公式的拟合。之前研究成果证明，单止屈器穿越压力与管道直径D、壁厚t、屈曲传播压力Pp均相关。加上双止屈器模型穿越压力大小依赖于止屈器间距及两个止屈器尺寸，因此将双穿越破坏压力按式(5)表示：

根据白金汉(Buckingham)π定律，将D和t作为基本量纲，对式(5)进行无量纲化，得：

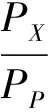
由于海底管道的PX≥PP，因此A0=1。为降低拟合的难度，将n>1的各情况省略后，得到近似关系为：

再通过将止屈效率公式(3)带入式(8)，得到止屈效率的近似公式(9)：

式中：αi(i=1～5)为待定相关系数。

采用最小二乘曲线拟合的方法，得到有限元结果与拟合结果关系散点图，如图10所示。图中随止屈器模型的几何尺寸增加，止屈效率结果的离散性逐渐显著，特别是在止屈效率大于1.1范围内，止屈效率与拟合公式的关系不再呈现出递增的态势。基于双止屈器结构优化设计的目的是得到止屈效率在1.0附近、能使整体结构重量最轻的结构型式，因此为提高拟合曲线的精度，在数据处理阶段去掉止屈效率超过1.1的各计算结果，重新拟合止屈效率公式，结果如式(10)所示。

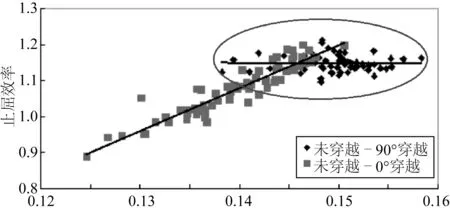
图10 双止屈器结构止屈效率的拟合Fig. 10 Fitting result of arresting efficiency

经计算，该公式的相关系数r=0.904 4，可决系数R2=0.891 1，拟合优度理想。另外，随机抽取10组拟合公式计算结果同有限元结果对比，误差均在5%以内，计算结果较为可靠。将式(10)带入至约束条件(4)中，作为双止屈器结构优化设计的止屈效率取值依据。

3.1.4 最终模型

由于双止屈器结构中设计参数众多，采用控制单一变量的方法逐一确定设计变量范围困难较大。考虑采用遗传算法与BP神经网络结合的方法，不预设止屈效率的显性表达式，以双止屈器结构重量作为适应度值，利用神经网络的强大非线性拟合能力和遗传算法的非线性寻优能力，寻找双止屈器模型的最优结构尺寸。在BP神经网络中，虽然通过遗传算法可选取最优初始权值及阀值，但训练及测试数据是在已有数据中随机选取的。该方法会导致每次的最优结果有所区别，因而不能将某次的优化结果作为最优双止屈器结构尺寸。鉴于通过BP神经网络方法得到的结果理论上均为所选变量域内的最优解，因此可通过统计BP神经网络计算得到的一系列最优结果的范围，作为设计变量的上下限约束值。

依据该思路，最终确定设计变量的取值范围如表2所示。

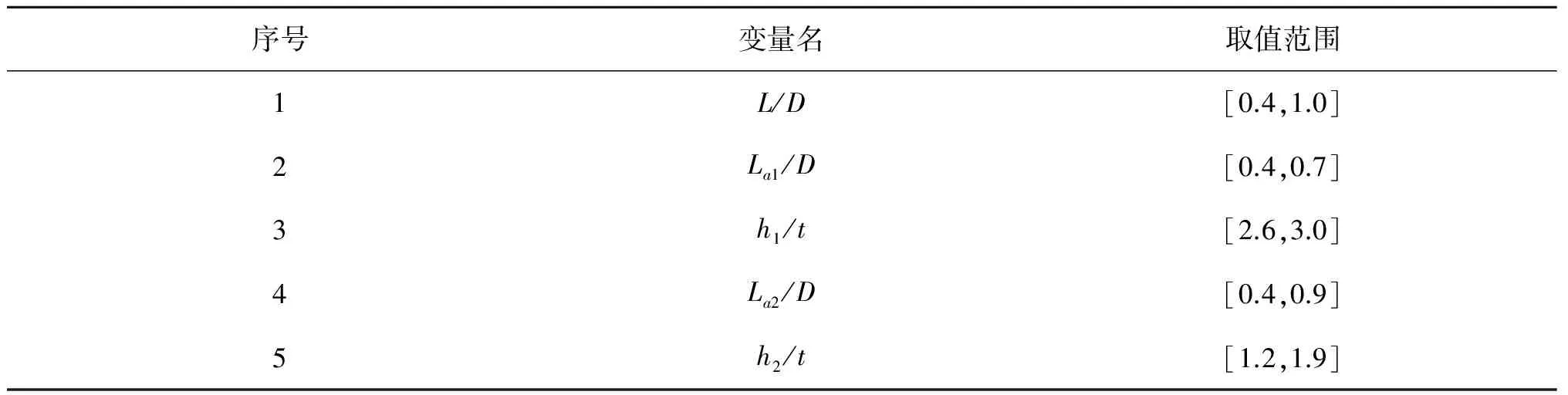
表2 设计变量范围Tab. 2 Scope of design variables

通过前述分析，最终确定止屈器优化设计的数学模型如式(11)所示：

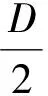
3.2优化结果

依据非线性有约束优化理论，采用经典算法和遗传算法分别对优化模型(11)进行求解，结果如表3所示。

表3 最优结果对比表Tab. 3 Comparison of optimal solution

经比较，两种算法结果基本一致。最优结构中第一止屈器厚度较厚、两止屈器间距较近，符合敏感性研究结果。

3.3最优型式的进一步分析

利用数值仿真模拟最优结构的屈曲穿越过程。在Abaqus中根据优化得到的参数建立最优双整体式止屈器结构的有限元模型，如图11所示。

图11 最优双止屈器结构模型Fig. 11 Optimal model of double-integral buckle arrestors

通过Abaqus模拟最优双止屈器在静水压力中的穿越过程，得到的止屈效率为99.15%，对比拟合公式计算值100%，二者间差异仅为0.86%，认为通过优化设计得到的最优双止屈器结构型式满足要求。

考虑到双止屈器模型可能出现由于结构重量大、制造费用高而影响其实际应用的问题，以经济指标为判断依据，就制造费用对相同止屈效率的最优双止屈器结构型式与单止屈器型式进行对比。

以有限元结果作为最优双整体式止屈器的止屈效率，即η优=99.15%，将单止屈器厚度取为双止屈器中第一个止屈器的厚度，即h1=3.0t。经不断试算得到当单止屈器长度为1.00D时，其止屈效率与最优双止屈器结构止屈效率相当。分别计算单止屈器和双止屈器结构的重量，比较在止屈性能相当的情况下，二者由重量引起的实际铺设难易。h为单止屈器厚度，La为单止屈器长度，钢材密度ρ为7 850 kg/m3。

1)单止屈器：

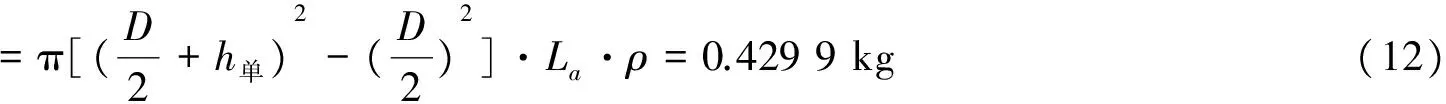
2)双止屈器：

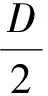
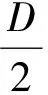
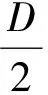
经计算，发现对于同一预期止屈效率，最优双整体式止屈器结构的重量低于单整体式止屈器，具有明显的重量优势。可见，在止屈器深水领域适用性问题的研究上，除了制造成本之外，设备重量具有更为重要的意义。尽管在制造和铺设过程中，双止屈器方案肯定更为耗时与昂贵，但其重量较低的优势使管道能够更易铺设与应用。

4 结 语

本文对双整体式止屈器进行了一系列止屈性能的研究，得到如下结论：

1)双整体式止屈器根据止屈器刚度及布置间距差异，在屈曲穿越时会产生六种不同的穿越破坏模式。

2)止屈器布置间距对整体结构的穿越破坏压力影响显著。近间距双整体式止屈器结构具有明显的止屈性能优势。

3)相较于第二个止屈器，第一个止屈器长度及厚度对整体结构的穿越破坏压力影响显著。在双止屈器结构的实际设计中，可适当增加第一个止屈器尺寸、减小第二个止屈器尺寸，以在保证止屈性能的前提下减轻结构重量，最大化地降低安装难度。

4)采用最小二乘曲线方法拟合得到双整体式止屈器止屈效率拟合公式，其变量均为双止屈器特征参数的无量纲化形式，适用性较广，可对除本文外的双止屈器模型止屈性能进行有效预测。

5)以整体结构重量最低为目标，止屈效率尽可能接近1.0为约束条件，建立最优双整体式止屈器结构优化设计的数学模型，得到最优设计参数。通过对比，认为最优双止屈器结构无论在止屈性能还是经济成本上，均具有明显优势。

[1] NETTO T A, ESTENFEN S F. Buckle arrestors for deepwater pipelines[J]. Marine Structures, 1996, 9(95): 873-883.

[2] 汪红艳, 陈晓贤, 林金保, 等. 深水海底管道止屈器设计研究[J].中国造船, 2011, 52(z1): 123-131. (WANG Hongyan, CHEN Xiaoxian, LIN Jinbao, et al. The design of internal buckle arrestors on deepwater pipelines.[J]. Shipbuilding of China, 2011, 52(z1): 123-131.(in Chinese))

[3] LEE L H, KYRIAKIDES S, NETTO T A. Integral buckle arrestors for offshore pipelines: Enhanced design criteria[J]. International Journal of Mechanical Sciences, 2008, 50(6): 1 058-1 064.

[4] PARK T D, KYRIAKIDES S. On the performance of integral buckle arrestors for offshore pipelines[J]. International Journal of Mechanical Sciences, 1997, 39(6): 643-669.

[5] KYRIAKIDES S, PARK T D, NETTO T A. On the design of integral buckle arrestors for offshore pipelines[J]. Applied Ocean Research, 1998, 20(1): 95-104.

[6] 翟宇轩, 余建星, 孙震洲, 等. 海底管道整体式止屈器的止屈性能研究[J]. 天津理工大学学报, 2014(5): 46-51. (ZHAI Yuxuan, YU Jianxing, SUN Zhenzhou, et al. The arresting perfbrmance of integral buckle arrestors for offshore pipelines[J]. Journal of Tianjin Unversity of Technology, 2014(5): 46-51.(in Chinese))

[7] MANTOVANO L O, AMENTA P. Finite element modeling and experimental validation of buckle arrestors for deepwater pipelines.[J]. Mecnica Computacional, 2006, 6(1): 687-706.

[8] TOSCANO R G, MANTOVANO L O, AMENT P M, et al. Collapse arrestors for deepwater pipelines. Cross-over mechanisms[J]. Computers & Structures, 2008, 86(78): 728-743.

[9] NETTO T A, KYRIAKIDES S. Dynamic performance of integral buckle arrestors for offshore pipelines. Part I: Experiments[J]. International Journal of Mechanical Sciences, 2000, 42(7): 1 405-1 423.

[10] NETTO T A, KYRIAKIDES S. Dynamic performance of integral buckle arrestors for offshore pipelines. Part II: Analysis[J]. International Journal of Mechanical Sciences, 2000, 42(7): 1 425-1 452.

[11] 余建星, 林晓龙, 杨源, 等. 深水海底管道整体式止屈器屈曲动态传播及止屈研究[J]. 海洋技术学报, 2013, 32(2): 60-65. (YU Jianxing, LIN Xiaolong, YANG Yuan, et al. Dynamic performance of propagation buckle and integral buckle arrestors in offshore pipelines[J]. Journal of Ocean Technology, 2013, 32(2): 60-65.(in Chinese))

[12] LEE L H, KYRIAKIDES S, NETTO T A. Integral buckle arrestors for offshore pipelines: Enhanced design criteria[J]. International Journal of Mechanical Sciences, 2008, 50(6):1 058-1 064.

[13] WANG H, SUN J, JUKES P. FEA of a laminate internal buckle arrestor for deep water pipe-in-pipe flowlines[C]// ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering. America: American Society of Mechanical Engineers, 2009: 447-452.

[14] MANSOUR G N, TASSOULAS J L. Crossover of integral-ring buckle arrestor: Computational results[J]. Journal of Engineering Mechanics, 2014, 123(4): 359-366.

[15] 李旭, 李庆, 张英. 深水海管止屈器设计方法研究[J]. 海洋工程装备与技术, 2014, 1(3): 227-229. (LI Xu, LI Qing, ZHANG Ying. Deepwater pipeline arrestor design study[J]. Ocean Engineering Equipment and Technology, 2014, 1(3): 227-229.(in Chinese))

[16] KYRIAKIDES S, BABCOCK C D. On the “Slip-On” buckle arrestor for offshore pipelines[J]. Journal of Pressure Vessel Technology, 1980, 102(2):188-193.

[17] 罗超, 王琮, 任翠青. 海底管道整体式止屈器结构设计及数值模拟[C]// 第十五届中国海洋(岸)工程学术讨论会论文集(上). 太原, 中国: 海洋出版社. 2011: 363-367. (LUO Chao, WANG Zong, REN Cuiqing. Structure design and numerical simulation of intergral buckle arrestors on deepwater pipelines[C]// Proceedings of the Ffifteenth China Ocean (Coastal) Engineering Symposium (Volume 1). Taiyuan, China: China Ocean Press, 2011:363-367.(in Chinese))

Arresting performance analysis and optimum design for the structure of double-integral buckle arrestors

WU Mengning1, 2，YU Jianxing1, 2, SUN Zhenzhou1, 2, DUAN Jinghui1, 2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety ,Tianjin University, Tianjin 300072, China; 2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)

1005-9865(2017)02-0056-11

P751

A

10.16483/j.issn.1005-9865.2017.02.009

2016-03-04

国家自然科学基金资助项目(51239008)；国家重点基础研究发展计划资助项目(973)(2014CB046805)；国家自然科学基金创新研究群体科学基金资助项目(51321065)

吴梦宁(1991-)，女，天津人，硕士研究生，从事海洋工程专业研究。E-mail：Lv_yico@163.com