不同界线符号实部相交的自动化处理方法

尤西霞，李成名，武鹏达，殷 勇

(中国测绘科学研究院，北京100830)

不同界线符号实部相交的自动化处理方法

尤西霞，李成名，武鹏达，殷 勇

(中国测绘科学研究院，北京100830)

制图规范中要求不同界线实部相交，然而当前制图软件多未考虑界线相交处虚线的处理，而且国内外文献针对实部相交的研究较少，尚未形成完整的解决方案，基于此，本文根据单元循环配置法绘制地图线状符号的基本思想，首先拆分原始单元块，然后分解原始的数据图层，最后将新单元块和新图层对应配置，并据此设计了自动化处理方法。通过实际数据验证了算法的有效性和合理性，该方法顾及了不同等级、不同类别界线的差异，并通过自动化的处理方法提高了地图编辑的效率。

界线符号；单元循环配置；单元块；实部相交

界线作为地图诸多要素中最基本的要素之一，是国家实施有效行政管理必不可少的依据[1]。制图对象中的界线主要包括：政治区界线、行政区划界、地理区域界，甚至还有经济、人文区域界等[2]。在制图规范中，界线的表示方法要求：境界线的形状按实地位置描绘，其转折处用点或实线段绘出，境界交会处也应当是点或实线[3]，当不同界线相交时，最好能保证其实线部分相交。

目前，现有的制图软件(如ArcGIS、MapGIS等)中的界线符号，只是由固定单元块沿着界线循环配置而成，后期依赖制图人员用CorelDRAW、AI等软件进行界线相交处虚线的处理。国内学者中鲜有提出解决方案，其中张晓通提出利用配对法[4]，找到与线目标相连的同一符号的线目标，并通过调整符号模板的长度，保证线末端以实部结束，这种方法对于不同等级的界线相交不适用，并且要动态进行配对，比较耗时，而且显示速度较慢。本文根据单元块线状符号设计的循环配置的基本思想[5]，从符号绘制的根本方法入手，在原始符号单元块基础上分解出半实部单元和去半实部单元，在相交的结点处，按照弧段端点与结点的关系，截取相应的长度，并输出到新的数据图层中，最后将不同图层的数据按照对应的单元块进行配置，从而解决绘制中要求的不同等级界线符号实部相交的自动化处理问题。

1 界线符号式样

不同制图规范中符号长度、宽度、面积等有差别，本文中以第一次地理国情普查数据作为试验数据，以2016年国务院全国地理国情普查领导小组下发的第9号文件《地理国情普查成果图技术规定》[6]为制图规范。图1为规范对于不同种类界线的符号样式的规定。

从图1可看出，界线符号具有共同的特征：都是实虚相间的线符号，只是实部、虚部的具体特征不同。本文所讲到虚线包括一线一点、一线多点、多线多点等多种组合的虚线；实部指的是符号中的实线，虚部指与实线相邻的点及空白。制图规范中要求的界线实部相交，就是指与不同界线在相交处需为符号中实线的一部分，而非空白；同时还要求在重复单元长度大致相等的前提下保证符号的完整性。

因为国界关乎我国的政治主张与外交立场，稍有不慎会带来不可估量的后果[7]，因此国界线绘制的基本规则和规范与其他符号并不完全相同，所以本文并不考虑国界这种特殊的界线，只对其他一般行政区界线进行处理。

2 单元块的拆分和绘制

界线符号属于符号数据模型中的线状符号数据模型。目前的研究中成果中，线状符号的设计方法一般分为3种[8]：单元循环配置法(横向循环配置法)、线型叠加法(纵向线型叠加法)和函数法(程序法线符号)。根据图1中界线符号的构图规律来看，可以根据单元循环配置的方法绘制界线符号。

2.1 单元块

单元块是指线状符号可以由固定图元块沿着线状要素的骨架线循环配置而成[9]，实质就是最小的循环单元。图2中列举了几种界线符号，第三列矩形框内为其对应的单元块(包括实线、实线间空白、点、点前空白及点后空白)。

图2 几种界线符号和其对应的单元块

2.2 单元块的拆分

要保证实部相交，需要在交点处均配置实线，若将原始符号中的线段直接放到交点处，会使符号化后的虚线中出现明显的过长实线段，不符合地图制图的基本原则。因此，需要将一个完整的单元块拆分为半实部和去半实部两部分，这样在交点处一个半实部加上一个去半实部，恰好能组成一个完整的符号单元，其中，半实部指的是原始单元块实线长度的一半，去半实部指的是原始单元块除去半实部以后剩余的部分。

图3列举了图2单元块对应的半实部单元和去半实部单元，并在图上标注对应的长度(单位为mm)，其中(a)单元块的线宽为0.5 mm，(b)、(c)单元块的线宽为0.4 mm，(d)单元块的线宽为0.3 mm。

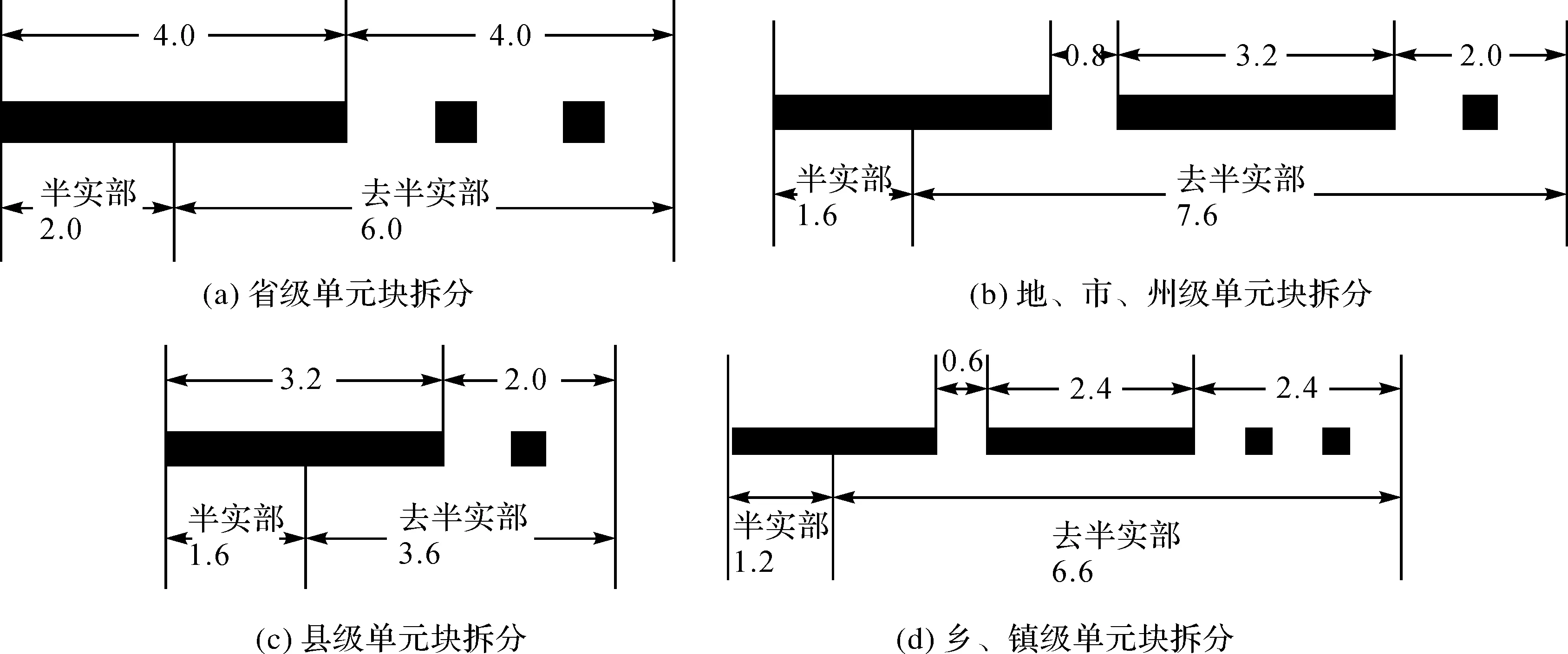
图3 几种行政区界线单元块的拆分

2.3 单元块的绘制

图3中不同界线的单元块、半实部单元块、去半实部单元块的绘制方法大致相同，以省级行政区界线的原始单元块为例进行说明：

步骤1：在编辑器中新建符号库-地理国情线(全开)，并添加分类5-行政区划与管理单元。

步骤2：确定符号的编号22，可改线宽0.5(单元块的线宽)，符号的宽度和高度8(一个单元块的总长度)，符号名称：省级界线，绘制方式：循环配置，符号颜色43(即黑色)。

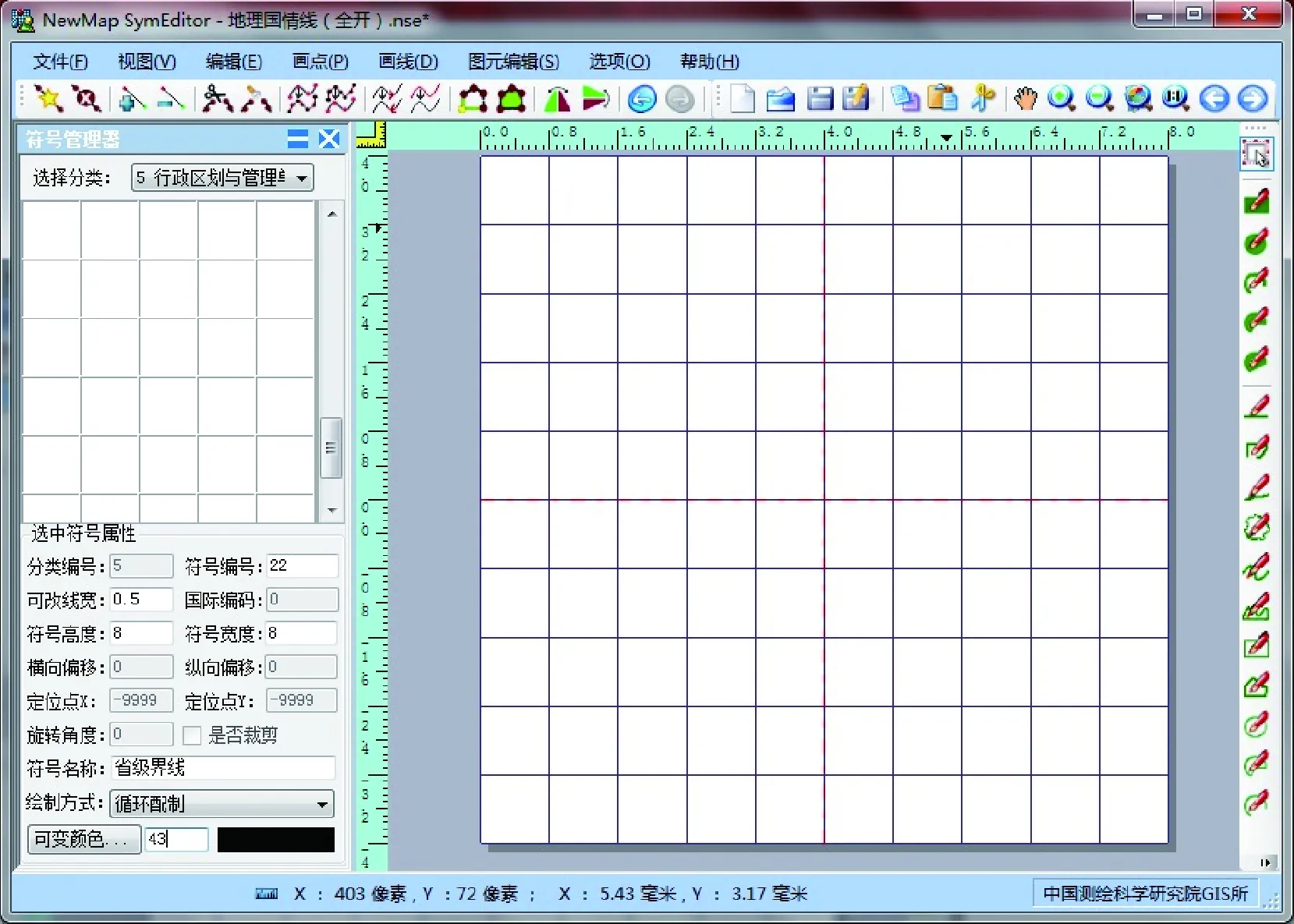
图4 配置符号参数

步骤3：选择菜单中选项-键盘输入图形，根据单元块上3条线的位置分别输入相应的起始点坐标，点击确定，坐标原点为(0,0)，其中的点为边长等于0.5 cm的正方形。图5中前3幅图依次为键盘输入线时起始点坐标，最后为编辑完成的最后效果。

步骤4：编辑完成后右键-保存为新符号即可。

3 数据图层的拆分

3.1 对界线原始数据的预处理

3.1.1 统一方向

首先将同一图层的界线方向统一为顺时针方向或逆时针方向，具体方法不在本文中描述。若不进行此操作，交点恰好均为所关联的2条同类界线的起点或终点，会在交点处全部配置为该界线所对应的半实部单元或去半实部单元，从整体看并不是正确的循环单元。图6以地、市、州级行政区界线(L1、L2)与县级行政区界线(L3)相交为例，在交点A处，由于L1、L2的起点均为A点，因此在矩形框区域内，配置的均为地、市、州级行政区界线的去半实部单元，从整体来看，导致在交点处的循环单元中多出一条实线，不符合制图规范，因此必须将同一图层的界线数据统一方向。

3.1.2 构建点线拓扑

每条弧都有一个首结点和一个末结点；每个结点都有一个弧的链表，记录与该结点相连的弧。只与结点和弧相关的拓扑称为点线拓扑[10]。本文中，建立点线拓扑的主要步骤为：弧段自相交处理、弧段之间相交的处理、去除冗余节点、结点拟合、去除重复弧、去除假结点、延伸长悬线、删除短悬线。建立点线拓扑后，就可以得到每个结点关联的弧段信息。

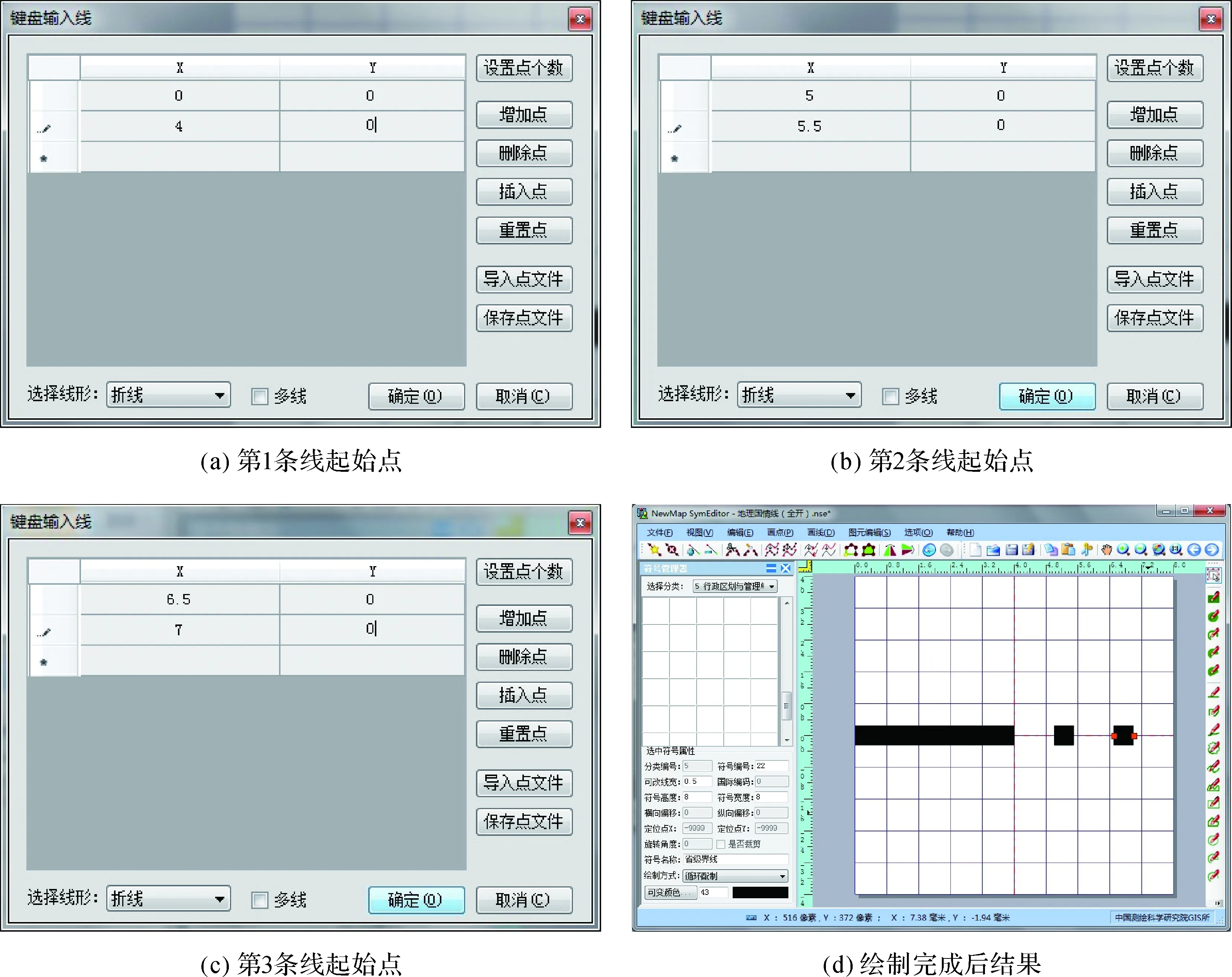
图5 单元块的绘制

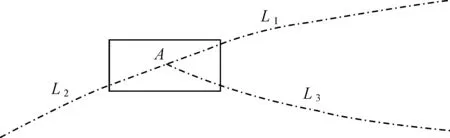
图6 同类界线在交点处均配置去半实部单元

3.2 结点处弧段的拆分

对于结点处关联的每条弧段进行相似的处理：

(1) 根据弧段L所在图层DataStore，得到其所对应的半实部单元的长度HalfLength和去半实部单元的长度RestLength。

(2) 判断结点A为L的起点还是终点。若为起点，则进行步骤a；若为终点，则进行步骤b:

a. 从A起沿L方向截取RestLength，将截取的弧段存储到去半实部输出图层RestStore中；

b. 从A起沿L的反方向截取HalfLength，将截取的弧段存储到半实部输出图层HalfStore中。

(3) 将截取后剩余的弧段存储到正常界线输出图层NormalStore中。

通过这样的处理以后，每一个DataStore被分解为RestStore、HalfStore、NormalStore 3个图层。

3.3 图层拆分的程序实现过程

(1) 定义分割点信息的结构体PointInformation，包含成员变量Split1(从起点沿弧段截取RestLength得到的分割点)、Split2(从终点沿弧段反方向截取HalfLength得到的分割点)、FirstIndex(Split1前一点的索引)、SecondIndex(Split2前一点的索引)，后文会涉及弧段重新组装的过程，由于线上的点只能通过点的索引得到，因此必须记录点的索引。还需定义map容器SplitPointsMap，使当前处理弧段和弧段上分割点信息相对应。如图7所示，弧段由P0～P(N-1)的N个点组成，从起点0截取RestLength长度得到分割点Split1(位于Pi和P(i+1)之间)， FirstIndex的值为i；从终点沿弧段反方向截取HalfLength长度得到分割点Split2(位于Pj和P(j+1)之间)，SecondIndex的值为j。

(2) 定义每个图层用来存储截取的半实部弧段容器HalfArcVec，去半实部弧段容器RestArcVec，正常弧段容器NormalArcVec。

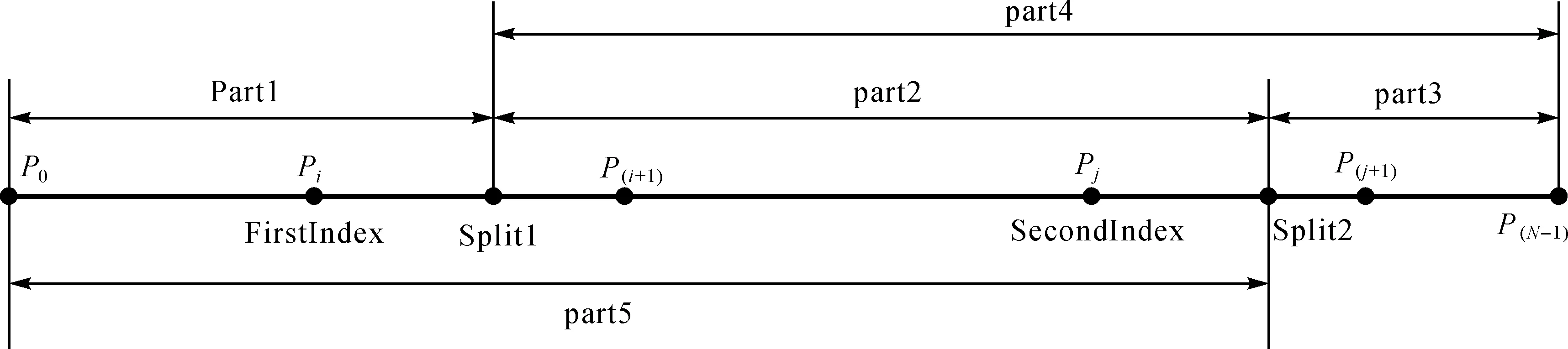
图7 弧段分割示意图

(3) 外部for循环每个结点，若当前节点关联的所有弧段属于同一图层，则将每条弧段放入原始图层对应的NormalArcVec中(保证处理的为不同界线)；内部for循环结点Node关联的每条弧段，对于长度小于一个单元块长度的弧段不作处理，直接放入图层对应的NormalArcVec中。

对于当前处理弧段Arc，若Node为Arc的起点，计算Split1和FirstIndex；若Node为Arc的终点，计算Split2和SecondIndex；并将处理过的弧段放入SplitPointsMap中。

(4) 结点循环完毕后，所有的弧段都已处理，然后for循环SplitPointsMap中的所有值，其中弧段所对应的分割点信息有以下3种情况：

a. 只有Split1一个分割点，说明该弧段为悬挂弧，并且终点只关联当前弧段；

b. 只有Split2一个分割点，说明该弧段为悬挂弧，并且起点只关联当前弧段；

c. 有Split1、Split2两个分割点。

如图6中所示，将弧段上从P0～Pi之间的点(包含首尾点，下文同此)及点Split1组成新的弧段用part1表示；由Split1、P(i+1)～Pj、Split2组成新的弧段用part2表示；由Split2和P(i+1)～P(N-1)的点组成新的弧段用part3表示；由Split1、P(i+1)～P(N-1)组成新的弧段用part4表示；由P0～Pj、Split2组成新的弧段用part5表示。

对于以上3种不同情况，处理方式分别为：

a. 将原始弧段组装为新的弧段part1、part4两部分，并将part1放入图层对应的RestArcVec中，part4放入图层对应的NormalArcVec中。

b. 将原始弧段组装为新的弧段part3、part5两部分，并将part3放入图层对应的HalfArcVec中，part5放入图层对应的NormalArcVec中。

c. 将原始弧段组装为新的弧段part1、part2、part3这3部分，并将part1放入图层对应的RestArcVec中，part2放入图层对应的NormalArcVec中，part3放入图层对应的HalfArcVec中。

(5) 利用拓扑标准化输出，分别将不同图层对应的RestArcVec、HalfArcVec、NormalArcVec中的弧段输出到原始图层对应的RestStore、HalfStore、NormalStore这3个图层中。

4 符号的配置

(1) 半实部单元的配置。由于原始DataStore分解出的HalfStore中每个弧段的长度与半实部单元长度相同，因此，恰好能配置一个图层相对应的半实部符号。

(2) 去半实部单元的配置。同半实部单元的配置方法相同，RestStore中的每条弧段，恰能配置一个完整的去半实部符号。

(3) NormalStore图层中符号的配置。对于图层中每条弧段，根据弧段长度自动调整单元块的长度，从而保证能循环配置完整个符号的长度，这种微调对于一条完整的弧段来说是极其微小的调整，几乎看不到其变化。

5 试验过程及分析

本文选取第一次地理国情普查数据中某县综合到1∶100 000后的境界层数据作为试验数据，符号的制作要求为图2中第3列中列举的规范。基于VC++平台开发的WJ-Ⅲ自动制图综合平台，编辑并存储所需要的符号单元，然后将算法的实现程序嵌入其中。算法调用的XML文档主要包含以下内容：

(1) 需要处理的边界线图层路径。

(2) 定义各图层对应的半实部单元和去半实部单元长度。

(3) 制图比例尺和构建点线拓扑时所用的容差值。

(4) 各图层对应的半实部数据、去半实部数据、原始单元块数据输出图层路径。

原始数据中A→B之间的线为省级行政区界线， B→A之间的线为县级行政区界线，内部的线为乡、镇级界线，图8(a)为原始界线的shape数据，图8(b)为直接配置不同图层对应的符号后得到的数据。

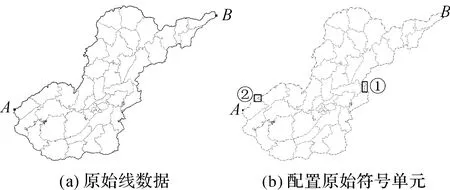
图8 处理前数据

将图8(b)中框①区域放大后，得到图9(a)；框②区域放大后，得到图9(c)；可看到在界线相交处，均没有实部相交。将图8(b)中A点周围区域放大后，得到图9(e)，在交点A关联的省级行政区界线弧段Arc1和县级行政区界线弧段Arc2的起点均为A，因此在A点出现了一个很长的实线部分；将图8(b)中B点周围区域放大后，得到图9(g)，在交点B处，两条关联的弧段的终点均为B，因此B点出现了3点聚集的情况。

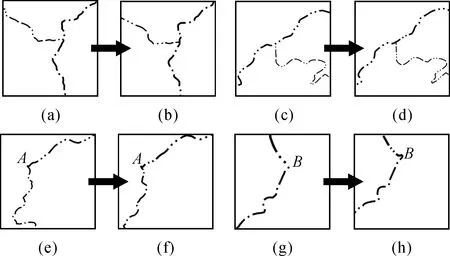
图9 处理前后对比

经过本算法的处理以后，框①、框②、点A、点B区域的处理结果分别对应中图9中的(b)、(d)、(f)、(b)，在交点处均实现了实部相交，并且从整体来看符号循环单元保持了一致性和完整性，并且具有良好的视觉效果。

6 结 语

本文从基本单元块的绘制入手，依据点、线的拓扑关系，通过对结点处的弧段进行拆分形成界线单元块新的组合单元：半实部单元块、去半实部单元块，并据此实现了不同界线符号在相交结点处的实部相交。依托中国测绘科学研究院研制的WJ-Ⅲ地图工作站，嵌入上述综合处理算法，以地理国情普查境界线为实验案例，进行了实部相交自动化处理。结果表明，本文提出的方法简单易行，提高了地图编辑的效率及实部相交的准确率。本文目前的研究仅针对不同界线相交时的符号处理，同种界线之间相交时会出现很多相邻闭合环，即使统一方向以后，公共弧两个端点处仍然会出现两个及以上弧段同时配置为半实部单元或去半实部单元，效果不是很好，有待进一步研究。

[1] 刘戎. 省级行政区域界线标准画法数据编辑方法研究[D]. 西安：西北大学，2005.

[2] 许华燕，殷国臣，王金月，等. 地图制图中界线套绘色带的原则[J]. 测绘与空间地理信息，2013，36(11)：203-207.

[3] 祝国瑞，郭礼珍，尹贡白，等. 地图设计与编绘[M]. 武汉：武汉大学出版社， 2001.

[4] 张晓通，朱海红，李霖. 境界符号中虚线实部相交问题的研究[J]. 测绘科学，2006，31(5)：104-106.

[5] 黄瑞阳. 地图符号共享关键技术研究[D]. 郑州：信息工程大学，2013.

[6] 地理国情普查成果图技术规定：GDPJ 17—2016[S].

[7] 周昕薇，张小霞，杨国东，等. 地图中的国界线绘制方法探析[J]. 测绘与空间地理信息，2013，36(11)：211-214.

[8] 骆琪. GIS与CAD地图符号共享方法研究[D]. 南京：南京师范大学，2012.

[9] 蔡先华，武利. 基于特征元的符号库数据结构及算法探讨[J]. 测绘学报，2004，33(3)：269-273.

[10] 程双伟. GIS中拓扑关系的建立与更新[D]. 郑州：信息工程大学，2002.

AutomaticProcessingMethodforDifferentBorderlineSymbolsIntersectingontheSolidPart

YOU Xixia，LI Chengming，WU Pengda，YIN Yong
(Chinese Academy of Surveying and Mapping，Beijing 100830，China)

According to the Specifications for Cartographic Symbols, different borderline symbols should intersect on the solid part. However, most of graphics software doesn’t consider the problem and few research articles are devoted to finding a complete solution. Based on the principle of cell cycle configuration method to design symbol, this paper provides a new algorithm to realize the intersecting of solid parts in the dashed line and designs an automatic processing method. First, the original cell block is split into two parts. Then, the original data layer is broken up into three new layers. Finally, match the new cell block with the new data layer. Practical data are used to validate the method. The results show that our method is highly reasonable and efficient. This paper provides an automatic processing method to improve the efficiency of map editing which takes into account of different grades and different types of borderlines.

borderline symbols; cell cycle configuration; cell block; intersecting on the solid part

尤西霞，李成名，武鹏达，等.不同界线符号实部相交的自动化处理方法[J].测绘通报，2017(10)：62-67.

10.13474/j.cnki.11-2246.2017.0317.

2017-02-08；

2017-08-21

国家科技支撑计划(2015BAJ06B01)；测绘地理信息公益性行业科研专项(201512020)；中国测绘科学研究院基本科研业务费项目(7771606)

尤西霞(1991—)，女，硕士生，研究方向为自动化制图综合和空间数据处理与挖掘。E-mail：yxxgis@163.com

李成名。E-mail: cmli@casm.ac.cn

P28

A

0494-0911(2017)10-0062-06