一种非接触式的标准圆柱齿轮参数测量方法*

王延忠，陈振鹏，唐 文

(北京航空航天大学 机械工程及自动化学院，北京 100191)

1001-2265(2017)10-0037-05

10.13462/j.cnki.mmtamt.2017.10.009

2016-12-04；

2017-01-09

国家自然科学基金资助项目(51275020); 国家科技支撑计划课题(2014BAF08B01)

王延忠(1963—)，男，沈阳人，北京航空航天大学教授，博士，研究方向为航空航天动力传动、摩擦润滑，(E-mail)yzwang63@126.com；通讯作者：陈振鹏(1990—)，男，福建泉州人，北京航空航天大学硕士研究生，研究方向为机器视觉，(E-mail)chenzpbj@163.com。

一种非接触式的标准圆柱齿轮参数测量方法*

王延忠，陈振鹏，唐 文

(北京航空航天大学 机械工程及自动化学院，北京 100191)

齿轮传动具有传动效率高、传动比恒定、功率和速度适用范围广等优点，在工业产品中广泛应用。齿轮的精度直接影响到工业产品的品质。目前齿轮参数的测量主要采用三坐标测量仪、CNC齿轮测量中心等接触式测量方法。这些接触式测量设备的使用和维修成本均较高，不便于大范围推广。基于机器视觉技术的非接触测量方法，具有实时、高效以及不损害齿面等优点，且随着摄像设备不断改进发展，测量精度大大提高。将机器视觉技术用于齿轮的测量中，提出了一种非接触式的标准圆柱齿轮参数检测方法，对齿轮的几何参数和部分单项误差进行了测量。

标准直齿圆柱齿轮；非接触式；机器视觉

0 引言

齿轮传动具有传动效率高、传动比恒定、功率和速度适用范围广等优点，在工业产品中应用广泛。齿轮的精度直接影响机械设备的性能与使用寿命[1]。对齿轮参数进行测量是加工生产中必不可少的环节。在工业生产上，采用基于机器视觉的非接触式齿轮参数测量方法，能有效避免接触式测量产生的表面损伤，并能提高测量效率和减少人为测量误差。

目前，齿轮测量技术主要以接触式测量为主。各种智能化的齿轮检测仪器，如CNC齿轮测量中心、齿轮在线测量分选机、超精密三坐标测量机等设备，具有柔性差、价格昂贵、技术性强等特点，不能得到大范围推广，迫切需要新的检测方式[2-5]。机器视觉是用机器模拟人眼对目标对象进行检测、识别、判断和测量的一种先进检测技术。文献[6-8]作者分别设计了基于机器视觉的测量系统，对标准直齿圆柱齿轮的直径、齿数等基本几何参数进行测量。当前基于机器视觉的齿轮测量技术仍在起步阶段。

本文设计了一种基于机器视觉的标准直齿圆柱齿轮的测量系统方案。该系统在Visual Studio平台下，运用双边滤波、边缘检测、形态学等图像处理方法，对标准直齿圆柱齿轮的基本几何参数及部分单项误差参数进行了测量，为齿轮参数的测量提供了一种柔性好、速度快、精度高和稳定性好的方法。

1 机器视觉测量系统设计

1.1 机器视觉测量系统

机器视觉测量系统如图1所示。该系统由CCD工业相机、高速摄像镜头、平行光源、物距调节结构以及计算机等设备构成，用于获取高质量的渐开线直齿圆柱齿轮数字图像。获取的部分齿轮数字图像如图2所示。

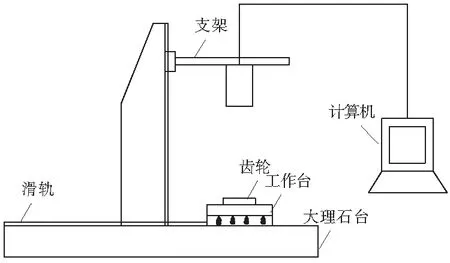
图1 机器视觉测量系统示意图

图2 齿轮数字图像

1.2 齿轮参数

本文主要对渐开线直齿圆柱齿轮的基本几何参数齿数z、模数m、分度圆半径r、齿顶圆半径ra、齿根圆半径rf以及部分齿轮单项误差等参数进行测量。

根据GB/T10095-2008，所测量的齿轮单项误差定义如下：

①单个齿距偏差Δfpt：在端平面上，在接近齿高中部的一个与齿轮轴线同心的圆上，实际齿距与理论齿距的代数差。

②齿距累积误差ΔFpk：任意k个齿距的实际弧长与理论弧长的代数差。

③齿距累积总偏差ΔFp：齿轮同侧齿面任意弧段(k=1 至k=z)的最大齿距累积偏差。

④齿厚偏差ΔES：在分度圆柱面上齿厚实际值与理论值的代数差。

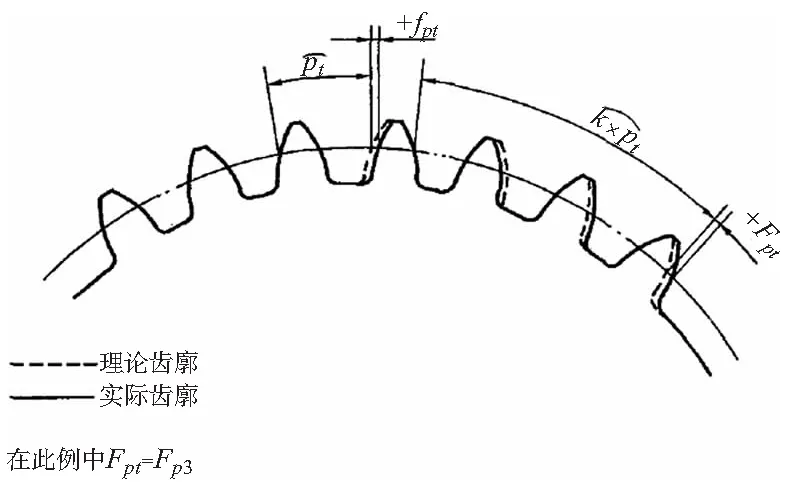
图3 齿距偏差与齿距累积偏差

2 齿轮参数测量

2.1 图像处理

(1)图像预处理

采集到的图像具有噪声，会对后续的边缘检测产生影响。因此需要对原图像进行滤波平滑处理，去除噪声点影响。本文选用双边滤波算法进行图像预处理。双边滤波公式[9-10]如下：

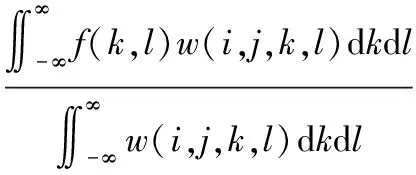
(1)

其中，权重系数w(i,j,k,l)取决于定义域核d(i,j,k,l) 和值域核r(i,j,k,l)的乘积。

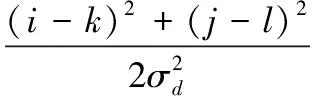
(2)

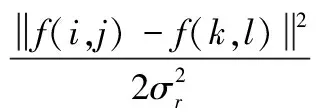
(3)

由上可知，双边滤波的特点是同时考虑空域信息和灰度相似性，达到保边去噪的目的，具有简单、非迭代、局部的特点。滤波前后的图像如图4所示。

(a)源图像 (b)滤波后的图像图4 双边滤波前后对比图

(2)图像二值化

图像二值化，即将图像上像素点的灰度值置为0或255。本文采用自动阈值法对图像进行二值化处理，效果如图5所示。

图5 二值化图像 图6 区域生长去除孔洞

(3)封闭区域孔洞消除

齿轮轮廓是研究的重点，为了去除齿轮孔洞等不必要轮廓的影响，需要采用封闭区域填充算法。常用的填充算法有多边形有序边表填充算法、种子填充算法及多边形边标志填充算法。

本文采用种子填充算法进行封闭区域孔洞消除。效果如图6所示。其基本流程如下[11]：

1)开辟堆栈，将圆心点O设为种子，压入堆栈；

2)当堆栈非空时：①从堆栈中弹出一个元素，并将该元素置为0；②遍历当前元素的八连通像素，检测此像素是否在边界之内，并判断该像素是否已被访问过；③若所测试的像素满足条件，则将该像素压入堆栈。重复进行①～③步骤直到堆栈为空或达到一定的迭代次数。

(4)边缘检测

边缘检测是齿轮参数测量关键的一步。所获得的齿轮轮廓边缘坐标越准确，实验数据就越可靠。本文选用Canny算子[12-13]对图像进行边缘检测，其基本流程如下：

1)首先对原图像进行滤波，以消除噪声；

2)采用2×2邻域一阶偏导的有限差分来计算平滑后图像I(x,y)梯度的幅值和梯度。其中沿x和y方向的偏微分如下式所示：

(4)

梯度幅值：

(5)

梯度相角：

(6)

3)根据边缘的方向，把边缘的梯度方向分为：0°、45°、90°和135°四个方向，找到该像素梯度方向的邻接像素；

4)非极大值抑制：遍历每个像素点，将其像素值与沿梯度线方向的两个像素值进行比较。如果该点的值比沿梯度线方向的两个相邻值小，则可判断该像素不是边缘点；

5)使用双阈值检测：如果像素的幅值大于高阈值，则该像素被保留为边缘；如果像素的幅值小于低阈值，该像素被排除；如果像素的幅值在两个阈值之间，该像素仅仅在连接到一个高于高阈值的像素时被保留。

使用Canny算子最终检测结果如图7所示。

图7 Canny边缘检测 图8 圆心定位

2.2 齿轮几何参数测量

(1)齿轮中心点O的测定

齿轮中心点的确定是以后齿轮几何参数测量的参考基准，本文采用的是重心法[14]进行检测。其基本流程是：设置初始(xo,yo)为(0,0)；对齿轮二值图逐行扫描图像像素，对像素值为0(齿轮区域)的坐标(xi,yi)，将其加入(xo,yo)，最后取平均值。公式如下所示：

(7)

其中，(xi,yi)满足f(xi,yi)=0。

(2)齿顶圆半径ra与齿根圆半径rf测量

计算齿廓边缘点距中心点O(xo,yo)的距离ri，并找到最大的前40个值，将其求平均，即为ra；齿根圆半径rf同理可得。

(3)确定齿数z

以长度(ra+ri)/2为半径设置掩膜模板，对齿轮二值化图像进行掩膜处理，得到只包括齿轮轮齿的图像。计算连通区域的个数，即可得到齿数z。

(a) 掩膜图像 (b) 部分轮廓图9 掩膜处理

(4)确定模数m

首先测得齿顶圆半径与齿根圆半径，然后由下式：

(8)

计算齿轮模数m。因为齿轮模数m是标准值，由计算结果在国标中查找与计算值之差最小的标准值，即为被测齿轮的模数。

(5)分度圆半径r

分度圆半径r由下式求得：

r=m×z/2

(9)

(6)角点检测

齿轮单项误差的测量，需要求出齿轮分度圆与齿廓交点的坐标。本文采用角点检测算法进行处理实现交点定位。

一般角点检测方法大致可分为两种：基于边缘的角点检测算法及基于灰度的角点检测算法[15-16]。前者需要对图像进行分割和边缘提取，处理过程较为复杂，且容易受噪声影响和边缘提取的依赖性的不足。而后者可以利用角点本身的性质检测角点，对图像其它局部特征没有依赖性。本文采用基于灰度图像的Harris算子角点检测方法检测角点。效果图如图10所示。

图10 角点检测

2.3 齿轮单项误差测量

(1)齿距偏差Δfft

由齿距偏差的定义，计算出各个实际齿距pi，将实际齿距pi与理论齿距p对比，即可求出齿距偏差[17-18]。其基本流程如下：

1)首先以确定好的齿轮中心O(xo，yo)为圆心，分度圆r为半径作圆。采用角点检测算法依次求出分度圆与齿轮轮廓的角点h1,h2,…,h2z，并求出各角点的坐标(x1,y1), (x2,y2), …, (x2z,y2z)。

2)由齿距定义可知，点(x1,y1)与(x3,y3)之间所夹的分度圆劣弧长即为齿距p1。同理，(x3,y3)和(x5,y5)之间所夹的分度圆的劣弧长为齿距p2。以此类推，就可得到所有的实际齿距pi，i=1,2,..z。

通过ArcGIS中ArcToolbox 计算出各农村居民点实际的最邻近点距离以及理论上的最邻近点距离。实际距离与理论距离的比值就是最邻近点指数，用于判定空间农村居民点整体分布模式[22]。指数计算公式：

由三角形余弦定理，实际齿距pi计算如下：

(10)

其中，i=1, 2, …,z。

3)理论齿距由下式可得：

p=π×m

(11)

4)求出实际齿距pi与理论齿距p的差值，其中的最大差值就是齿距偏差Δfpt。

Δfpt=max{p-pi|i=1,2,…,z}

(12)

(2)齿距累积误差ΔFpk

根据齿距累积误差的定义，可知其计算公式如下：

(13)

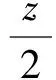
(3)齿距累积总偏差ΔFp：齿距累积偏差的最大值和最小值间的代数差。

ΔFp=ΔFpk(max)-ΔFpk(min)

(14)

(4)齿厚偏差ΔES

齿厚偏差ΔES计算原理同齿距偏差。其基本流程如下：

1)首先求单个齿厚：

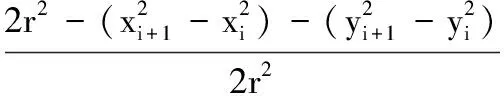
(15)

其中，i=1, 3, …,2z-1。

2)齿轮分度圆弦齿厚由下式可得：

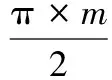
(16)

3)由下式计算齿距累计误差ΔES：

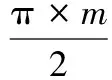
(17)

3 实验及误差分析

3.1 系统标定

本文采用量块来对系统进行标定。其基本流程如下：①在相同测量模型下，采集长度为L的量块图像；②对原始图像进行降噪预处理；③用Canny算子提取边缘；④通过Hough直线变换检测量块边缘，提取直线信息；⑤计算直线长度N(像素数)。最终得出本系统像素(pixel)与长度单位(mm)之间的转换关系：

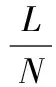
(18)

图11 试验量块宽度变动量最大允许值0.2mm)

3.2 实验结果分析

以标准直齿圆柱齿轮为试验样品，根据上述步骤测得齿轮的基本几何参数及部分单项误差。测量结果如表1所示。

表1 测量结果对比

3.3 误差分析

由实验可以看出，本测量系统还存在误差，具体分析如下：

(1)平行光源的强弱会引起测量误差；

(2)支架与大理石台面的设计与装配具有误差，无法绝对保证镜头与大理石台面的平行；

(3)光学镜头的畸变会影响CCD的成像质量与齿轮轮廓边缘的定位；

(4)标定块的精度影响标定结果，对像素尺寸转换为实际的物理尺寸有很大的影响；

(5)由于采集的图像以像素为最小单位，齿轮中心的定位、齿根圆半径及齿顶圆半径均存在像素级别的误差。

4 总结与展望

本文对基于机器视觉的齿轮参数检测系统进行了研究，运用图像处理相关算法，在Visual Studio平台下对齿轮的基本几何参数和部分单项误差进行了实测。试验结果表明，该方法对齿轮参数尺寸检测快速准确，检测精度达到了像素级别，测量误差均在允许的范围内，满足齿轮参数检测要求，对齿轮的实际生产制造具有一定的应用价值。

机器视觉技术是目前研究的热门，拥有广阔的发展空间。本文基于机器视觉技术，对标准直齿圆柱齿轮进行了测量分析。然而受到时间与试验设备等条件的限制，仍有很好的发展空间[19-21]：

(1)采用更高分辨率、更快帧率的CCD工业相机能极大地提高系统的精确性与实时性；

(2)齿轮测量参数众多，本论文只是对其中的部分参数进行测量分析，以后还可进一步研究，实现更多参数的测量；

(3)可将视觉测量扩展到其他齿轮，如螺旋锥齿轮的参数测量；

(4)相对于单目视觉来说，双目甚至多目视觉能获得更多的信息，甚至获得齿面的三维信息；

(5)研究亚像素级别的齿轮轮廓边缘检测算法，将测量精度提高到亚像素级别，减少测量误差。

[1] 赵韩,吴其林,黄康,等. 国内齿轮研究现状及问题研究[J]. 机械工程学报,2013,49(19):11-20.

[2] 石照耀,林虎,林家春,等. 大齿轮测量:现状与趋势[J]. 机械工程学报,2013,49(10):35-44.

[3] 石照耀,费业泰,谢华锟. 齿轮测量技术100年——回顾与展望[J]. 中国工程科学,2003,5(9):13-17.

[4] 石照耀,张万年,林家春. 小模数齿轮测量：现状与趋势[J]. 北京工业大学学报,2008,34(2):113-119.

[5] 韩连福. 齿轮测量中心若干关键技术研究[D]. 哈尔滨:哈尔滨工业大学,2015.

[6] 饶艳桃. 基于机器视觉的标准直齿圆柱齿轮参数的测量[D]. 重庆:重庆大学,2015.

[7] 沈海珍. 基于机器视觉的小模数齿轮轮廓信息提取算法研究[D].杭州:中国计量学院,2015.

[8] 杨丹. 基于机器视觉的齿轮测量技术研究[D].沈阳:沈阳工业大学,2015.

[9] Canny J. A Computational Approach To Edge Detection[J]. IEEE Trans. Pattern Analysis and Machine Intelligence. 1986,8(6): 679-714.

[10] Lindeberg Tony. Edge detection and ridge detection with automatic scale selection[J]. International Journal of Computer Vision,1998, 30 (2): 117-154.

[11] 余腊生,沈德耀. 扫描线种子填充算法的改进[J]. 计算机工程,2003,29(10):70-72.

[12] 张玲艳. 基于Canny理论的自适应边缘检测方法研究[D].西安:西北大学,2009.

[13] 王植,贺赛先. 一种基于Canny理论的自适应边缘检测方法[J]. 中国图象图形学报,2004,9(8):65-70.

[14] 谢红,廖志杰,邢廷文. 一种非接触式的圆孔形零件尺寸检测[J]. 电子设计工程,2016,24(19):155-158.

[15] 赵文彬,张艳宁. 角点检测技术综述[J]. 计算机应用研究,2006,23(10):17-19,38.

[16] 张功国. 角点检测技术综述[J]. 数字技术与应用,2013(4):157.

[17] 王文成. 基于机器视觉的齿轮参数测量系统设计[J]. 机械传动,2011,35(2):41-43.

[18] 程丽丽. 基于视觉技术的摆线齿轮参数及误差的快速测量系统研究[D].南宁:广西大学,2013.

[19] 魏锋. 立体视觉在准双曲面齿轮接触区检测中的应用[D].大连:大连理工大学,2007.

[20] 刘瑞玲,钟德星,韩九强. 汽车伞齿轮多目视觉检测系统与算法[J].西安交通大学学报,2014,48(4):1-7.

[21] 罗桂娥. 双目立体视觉深度感知与三维重建若干问题研究[D].长沙:中南大学,2012.

ANon-contactMeasuringMethodfortheParameterofStandardCylindricalGear

WANG Yan-zhong， CHEN Zhen-peng， TANG Wen

(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

Gear transmission has the advantages of high transmission efficiency, constant transmission ration, a wide range of power and speed. Gear is widely used in industrial products. The accuracy of gear directly affects the quality of industrial products. At present, the gear parameter measurement mainly uses the contact type. The current measurement of gear parameters includes coordinate measuring instrument, CNC gear measuring center and so on. However, these detection equipment is expensive, and difficult to use and maintenance. They have not been widely used. The non-contact measurement method based on machine vision technology has the advantages of high efficiency, good real-time, wide dynamic range and no damage to gear. With the continuous improvement of the camera equipment, the measurement accuracy is greatly improved. In this paper, the machine vision technology is applied to the measurement of gears. A non-contact method for measuring the parameters of standard cylindrical gears is proposed. The geometrical parameters and some individual errors of the gears are measured.

standard cylindrical gear; non-contact; machine vision

TH132;TG61

A

(编辑李秀敏)