考虑装置失效的高层建筑舒适度生命周期设计
2017-11-07王立林郑毅敏
赵 昕, 王立林, 郑毅敏
(1.同济大学建筑工程系 上海,200092) (2.同济大学建筑设计研究院(集团)有限公司 上海,200092)
10.16450/j.cnki.issn.1004-6801.2017.05.004
考虑装置失效的高层建筑舒适度生命周期设计
赵 昕1,2, 王立林1, 郑毅敏1,2
(1.同济大学建筑工程系 上海,200092) (2.同济大学建筑设计研究院(集团)有限公司 上海,200092)
鉴于个体对风致振动反应的不确定性及差异性,结合日本的AIJ(Aruitectural Institute of Japan,简称AIJ)标准,建立评价高层建筑风振舒适度性能水平的感振率模型,对基于可靠度理论的生命周期费用模型进行修正,并在模型中考虑了风振控制装置失效对结构舒适度性能的影响。利用修正模型对高层建筑调频质量阻尼器(tuned mass damper,简称TMD)、调频液柱阻尼器(tuned liguid column damper,简称TLCD)以及组合调谐阻尼器(combined tuned damper,简称CTD)安装与否进行投资决策。研究表明:考虑振动装置失效时结构1年内的感振率可达到不考虑装置失效时的1.4~3倍;基于修正模型进行各阻尼器方案比选时,CTD的减振效率和生命周期费用都介于TMD和TLCD之间,是个很有竞争力的选择。
高层建筑; 感振率模型; 生命周期费用模型; 风振控制装置失效; 调频质量阻尼器; 调频液柱阻尼器; 组合调谐阻尼器
引 言
基于性能的结构抗风设计(performance based wind-resistant design,简称PBWD)的目的是在不同强度水平风振作用下,能够有效地控制建筑结构的安全、舒适使用性能,使建筑物实现明确的不同性能水准,从而使建筑物在整个生命周期内,在遭受可能发生的风振作用下,总体费用达到最小[1]。为了更好地满足工程需求,国内外学者对PBWD进行了大量研究[1-4]。生命周期设计(life cycle based design,简称LCBD)是PBWD的一种重要思想。Sarja[5]对工程结构生命周期设计与维护及生命周期费用分析方面进行全面的研究,形成了较为完整的框架,指出结构设计不仅仅要考虑初始费用,还应考虑结构在使用过程中需要的维护费用,甚至包括结构失效以及拆除费用等。Frangopol等[6]研究了考虑桥梁等工程结构维护费用较高,提出了考虑维护费用的生命周期费用分析的模型,给出了某桥梁的最优检查维护方案。卜国雄等[7]对TMD结构的全生命优化设计进行了研究,采用了效-费比进行经济性评价。然而其未考察结构舒适度失效产生的费用,不能对结构的舒适度全生命周期费用进行评价,也未体现不同功能建筑物对舒适度要求的高低及相应的舒适度失效后果。鉴于此,笔者曾提出基于风振舒适度的高层建筑生命周期费用模型[8]。该模型能够很好地考察结构舒适度失效影响及不同功能建筑物的舒适度要求。遗憾的是,该模型建立在用日本建筑协会风振舒适度控制标准[9]和可靠度思想上,当结构加速度响应较大时,计算可能会出现较大偏差;更重要的是,该模型没有考察因TMD本身失效时对结构舒适度失效的影响。
笔者对基于风振舒适度的高层建筑生命周期费用模型进行改进,引入阻尼器本身失效对结构舒适度失效的影响,并基于AIJ标准建立了感振率模型用以计算生命周期费用克服数据处理时的大偏差现象,提高模型的普适性;此外改进后的生命周期费用模型也可用于配置其他风振控制装置时结构生命周期费用。以一个超高层建筑为例,探讨了分别配置TMD、调频液柱阻尼器和由笔者提出的组合调谐阻尼器[10]优化设计方案,以期为后期工程应用提供支持。
1 高层建筑生命周期费用模型
1.1 已有的高层建筑生命周期费用模型
由笔者提出的基于风振舒适度的高层建筑生命周期费用模型为
(1)
其中:C0为初始投资;Cm为检修维护费用;Cf为失效费用;Tlife为生命周期使用年限,对于超高层建筑一般可取100年;r为资金折现率;c1为1年内建筑结构因舒适度失效产生的费用。
超高层建筑结构在风荷载作用下产生振动,依据结构振动加速度水平可以将结构舒适度划分为若干性能水平等级,某一性能水平失效时会引起相应比例的人员感到不安和工作效率下降,从而直接或间接造成经济损失。若将结构风振舒适度性能水平划为n级,且设1年内第j级性能水平失效造成的损失为cj,结构发生第j级性能水平失效的概率为pf,j。则1年内,建筑结构因舒适度失效产生的费用c1为
(2)
上述模型是建立在可靠度分析基础上的,在应用该模型时,作者选取国际上普遍认可的AIJ标准。结构的风振舒适度性能可由1年回归期的风荷载作用下10 min内结构的最大振动加速度αmax来确定,其中αmax与振动频率有关,如图1所示。根据不同结构最大振动加速度可将结构在风荷载下的舒适度性能划分为“H-10”~“H-90”5个等级。其中,H-10

图1 日本的建筑风振舒适度标准[9]Fig.1 Horizontal vibration performance evaluation curves for buildings under wind load in Japanese criterion
表示10%的人感知振动,H-30表示30%的人感知振动,其余类推。由此可见多级性能目标在AIJ规范中得到了很好的体现,这比目前国内规范采用的与频率无关的单一限值准则更加合理。但对于强风作用地区结构,在各级水平风力作用下,加速度响应均较大,由可靠度理论知识可知,此时结构性能超过H-90的概率接近100%,这将与国内规范采用单一限值的效果等同。为了提高模型的普适性,文中从AIJ规范出发,引入反应感知振动等效人数比例的感振率模型对其进行改进。
1.2 基于感振率的生命周期费用模型
1.2.1 风振舒适度标准
为了便于说明,文中给出AIJ标准中结构加速度各性能指标阀值与振动频率的关系
(3)
其中:αmax为最大加速度响应(cm/s2);f1为振动频率(Hz);a和b为水平振动评估曲线的系数和指数(见表1)。
表1日本标准中风致水平振动评估系数
Tab.1EvaluationcoefficientsofhorizontalvibrationfortheJapanesecriterion

频率范围0.1≤f1<1.51.5≤f1≤2.52.5 由表1和图1可知,当结构的频率确定以后,各级性能目标对应的加速度限值可根据式(3)得出。1.2.2 一次振动作用下感振率模型 从心理物理学的角度,人对振动主观反应的不确定性可以被划分为两类:a.由于人的主观反应判断标准在概念上的不清晰所导致的模糊性;b.由于人对振动刺激敏感程度差异导致的随机性。 结合心理物理学的信号检测理论分析人对振动反应的不确定性。在振动舒适度实验和振动舒适度标准的基础上,归纳出描述人对振动主观反应模糊性的隶属度函数的统一数学表达式为 ν(u)=cln(u)+d (4) 其中:u为振动加速度;v为主观反应的概念隶属度值;c,d为待定系数。 由此可见,主观反应的概念隶属度值与振动加速度的对数值成正比,即心理物理学的Fechner定律。 Griffin等[11]认为,人对振动感受性的分布不拒绝正态分布和对数正态分布,类似的结果后来为其他研究人员所证实,总的认为对于人对振动感受能力的变异性可以先近似认为它服从对数正态分布 (5) 式(5)的物理意义是,在一个加速度为x的振动作用下,由于人感受性的差异,不同的人感受并不一样,人们实际感受的是一个加速度相当于u的振动刺激作用,这些感受到的刺激虽然彼此不同,但是总的统计平均仍然是一个相当于x的刺激作用。 结合振动感受性的实验研究,在心理物理学集值统计方法的基础上建立感振率的计算模型,并用感振率作为描述人对振动主观反应的量化指标。考虑到模糊性和随机性的分布特点,根据式(3),(4)给出振动加速度为x时的感振率计算式为 A(x)= (6) 感振率A(x)的物理意义是在某一振动作用下,对振动有感觉但不致有不适的振动程度的等效人数比例。 对于某建筑结构,当其频率f1已知时,便可根据选定的AIJ标准得到5个性能等级的加速度限值xi(i=1~5),将(x1,10%),(x2,30%),(x3,50%),(x4,70%),(x5,90%)代入式(6)即可求出其中的待定系数,进而求得风振感振率表达式。 1.2.3 年感振率计算模型 曹宏等[12]研究表明,用正态分布法描述结构的风振加速度反应峰值的概率密度分布较为恰当,在结构响应标准差已知时,感振率期望值,即在加速度响应随机分布的情况下的感振率可表示为 需要注意的是,上面的感振率期望值是在一定的平均风压w0下得到的[13],所以其计算的结果是在一定风压下的感振率期望值。因此,1年内强风作用下感振率期望值可表示为 (8) 为了方便计算,宜将式(6)作离散化处理 (9) 其中:F(wi)为一次强风的10 min最大平均风压的概率分布函数;m为将平均风压划分的等级数(《建筑结构荷载规范》给出了F(wi)的表达式)。 通过1.2.1~1.2.3的分析可知:感振率模型能够很好地反应任一特定结构的特定振动环境在1年里可能遇到的所有风荷载作用下的舒适度性能。 不同结构功能的建筑,同一振动水平造成的损失也不一样。例如,医院要求较高水平的振动舒适度,高档酒店、写字楼对舒适度要求也较高;而对于观光塔等来讲,对舒适度要求就相对较低,因舒适度失效造成的损失也就少一些。因此,对结构性能水平舒适性失效费用进行估算时,需要综合考虑结构使用功能,居住者人数,人员敏感程度和建筑物所在地当地经济条件水平等。 对于不同的建筑,建议的舒适度性能失效费用可以按下式计算 (10) 根据1.2和1.3节的分析可知:1年内,建筑结构因舒适度失效产生的费用c1为 (11) 为了对建筑结构整个生命周期进行考察,在综合评价时还需考虑资金折现的影响。为简化分析,可考虑时不变结构,各年发生失效的费用相同,得到如下生命周期舒适度费用评估模型 (12) 其中:C0为初始投资;Cm为检修维护费用;Cf为失效费用;Tlife为生命周期使用年限,对于超高层建筑可取100年;r为资金折现率;θ为反映决策者对风险态度的调整系数,(对于乐观型,θ>1;保守型,θ<1;中间型,θ=1。文献[14]认为,对于研究咨询机构等“风险中性体”进行的风险决策,取θ=1。) 为了提高建筑结构的舒适度,往往采用安装阻尼器装置减小结构的振动。合理布置阻尼器能够有效降低结构的响应加速度,进而提高结构的舒适度,阻尼器的作用效果可以通过减振系数表示,最终将在结构生命周期费用中体现。 定义阻尼器的减振系数为 (13) 阻尼器能够有效降低结构的风振响应,但在强风作用下阻尼器自身响应很大[16],可能引起自身或周边结构的损坏。因此,实际工程安装阻尼器时会配置限位装置,当阻尼器响应达到或超越限值时阻尼器将被锁定,从而造成阻尼器失效。在已有的研究[13-14,16]中,基于首次超越破坏理论,对于给定的位移限值b,阻尼器相对于结构的位移y(t)在时间T内超越界限b的次数的期望值为 (14) 当界限b很高时,y(t)在时间T内超越界限的事先属于稀有事件,可假定其服从Poisson分布。则阻尼器的动力可靠度(即超越次数N=0次)可表示为 (15) 以上是考虑单侧界限的阻尼器的动力可靠度,对于双侧对称的情况,则有 (16) 当相应的界限水平不是很高时,泊松过程的假设是不可以接受的。Vanmarcke[17]基于交叉次数为Markov过程的假设,提出了修正公式 Ps2(-b (17) 此时,阻尼器的失效概率为 Pf2=1-Ps2 (18) 需要注意的是,上面的安全界限是在一定的平均风压ω0下得到的[14],所以其计算的可靠度是在一定风压下的条件概率。因此结合结构所在地的风场环境分析,便可得到1年内强风作用下阻尼器的失效概率。 (19) 其中:f(ω)为1次强风10 min最大平均风压ω的概率密度函数。 由上文分析可知,对于不同的建筑,含阻尼器结构的舒适度性能失效费用可以按下式计算 (20) 1年内,建筑结构因舒适度失效产生的费用为 (21) 含阻尼器结构生命周期舒适度费用评估模型 (22) 式(22)中参数含义同式(12)。 采用阻尼器尽管会增加初始投资和检修维护费用,但失效费用却会降低,因此生命周期费用需要进行精细分析和计算。由于随着阻尼器质量增大,阻尼器造价增大;而减振效果先增大后趋于平缓,舒适度失效费用先减小后趋于平缓。因此存在阻尼器最优质量比使得生命周期费用取最小值,优化原理如图2所示。 图2 优化设计原理示意图Fig.2 Schematic diagram of the optimal design theory 从2.4节的分析发现,阻尼器的初始造价随着选用的阻尼器质量增大而显著的增大。因此,为了节省初始成本,需要合理设计阻尼器系统的参数以使之发挥最大的减振效果。同时合理的参数设置也会使得结构的各舒适度性能水平的失效费用降到最小,从而降低结构生命周期总费用。因此,基于风振舒适性能生命周期费用最小化的设计方法可以分为以下几个步骤: 1) 计算不同质量比的阻尼器系统最优控制参数,以充分发挥控制装置的效果; 2) 计算不同质量阻尼器结构的初始费用; 3) 按式(9)计算各方案结构舒适度性能水平感振率; 4) 根据式(12)或(22)计算结构生命周期总费用,并用总费用最小原则进行投资决策; 5) 校核结构是否满足业主确定的舒适度性能水平或规范要求,如不满足则调整阻尼器质量,返回第步骤4。 某141层建筑功能为集商业、办公以及酒店为一体的综合性超高层建筑。其结构高度为600 m,截面尺寸B=D=69 m,可根据文献[17]所示方法对原结构进行简化,原结构、简化后的质点串模型简图如图3(a)所示。其中:编号1~5代表伸臂编号,1~9代表环带编号;图3(b)中,mi,ki,ci分别代表各质点质量、刚度及阻尼(i=1~28))。结构的基本频率为0.11 Hz,计算舒适度时结构的阻尼比取为2%,当地的风环境为:C类地貌,50年一遇的基本风压w0为0.45 kPa。拟对结构舒适度性能进行评估,并对上文提及的3种振动控制方案进行决策。 图3 某超高层结构模型 将一年内可能出现的平均风压离散为:0.10,0.30,0.45,0.50,0.57,0.67 kPa 6个风力水平。为了考察TMD失效对结构的舒适度性能的影响,以配置1 500 t TMD的结构为例,计算风力水平为26.54 m/s(0.45 kPa)的横风向加速度响应标准差和感振率,如图4和5所示。由图4和图5可以看出,配置1 500 t TMD时特定风力水平下结构的加速度响应和感振率应有大幅降低,这说明结构性能有很大的改善。根据工程经验可知,配置TMD的结构在遭遇超过20年一遇的风荷载作用时将被锁定(视为TMD失效),基于文中对考虑和不考虑TMD失效结构舒适度性能水平进行了比较,如图6所示。由图6可以看出,在配置1 500 t TMD时,1年内结构的舒适度性能有很大提高;而考虑与不考虑TMD失效时,各楼层在1年内的整体舒适度水平相差可达到50%,即是说在考虑TMD失效时处于各振动环境中感受到振动的等效人数比例可达不考虑TMD失效时高出1.4~3倍,可见不考虑TMD失效时结构的舒适度性能评估是偏于乐观的,这对结构的舒适度性能经济评估影响是很大的。因此,在工程中为了更准确地评估各振动控制方案的经济效果,对阻尼器的失效影响加以考虑很有必要。下文将使用考虑阻尼器失效的生命周期费用模型对各阻尼器方案进行优化设计。 图4 横风力下结构加速度响应对比图(w=0.45 kPa)Fig.4 Comparison of standard deviation of structural acceleration under across-wind (w=0.45 kPa) 图5 横风力下结构感振率对比图(w=0.45 kPa)Fig.5 Comparison of vibration-sensation rate under across-wind (w=0.45 kPa) 图6 横风力下结构感振率对比图(包含所有风力水平)Fig.6 Comparison of vibration-sensation rate under across-wind (all levels considered) 获得结构舒适度性能水平的感振率后,可以用前面建立的生命周期舒适度费用模型进行评估,由于本结构横风向响应起控制作用,可按横风向进行计算,计算年限取100年,资金折现率取3.5%。为了比较含与不含阻尼器结构的生命周期费用,可将不含阻尼器装置的结构初始费用设为0,振动控制方案费用分析见文献[18]。则由结构舒适度生命周期费用分析模型可以求得,结构在计算年限内的费用如图7和表2所示。 图7 生命周期费用与阻尼器质量关系Fig.7 Life cycle costs with damper masses 设计方案阻尼器质量/tC0/万元Cm/万元Cf/万元LCC/万元无控结构7651.47651.4含TMD500700355467.46202.4含TLCD1000 14075782.65929.6含CTDTLCDTMD65035095.1489.950.5524.505455.86065.9 由此可见,安装阻尼器对结构舒适度性能有很大的改善,虽然初期投资增加了很多,但是从生命周期费用来看,结构总体费用反而降低。对比各方案生命周期费用发现,含TLCD<含CTD<含TMD<无控结构。因此,可以考虑选择安装阻尼器。值得注意的是,由于TLCD初始造价很低,随着TLCD质量的增大,生命周期费用持续减小。但TLCD所储液体通常为水,其所占体积是相同质量的TMD的数倍,这对建筑空间要求很高。综合起见,文中取TLCD,CTD均为TMD质量2倍。 利用前文所述的方法获得结构生命周期费用最小的结构方案,应满足业主的个性化风振性能水平要求或规范要求的限值。对于本例,分别计算结构在10年重现期下结构顶部加速度相应的标准差,然后依据结构响应的概率分布为均值为0的高斯正态分布,取峰值因子为2.5(保证率为99.3%),便可得到结构加速度响应峰值,计算结果如表3所示。 表3 各结构方案舒适度性能水平校核 由表3中数据可知,各阻尼器方案舒适度性能均满足我国规范对旅馆、办公楼的加速度水平限值,略大于规范对公寓的加速度水平限值要求。如果业主对塔楼舒适度性能水平提出了更高的要求,可以采用增大阻尼器质量等方法,以获取最优的结构设计方案。 算例表明,考虑TMD失效时结构1年内的舒适度水平可达到不考虑TMD失效时的1.4~3倍,这使得高达数百米的超高层建筑结构生命周期费用影响很大,因此在工程应用中应考虑阻尼器失效对生命周期费用的影响。 TMD,TLCD,CTD 3种阻尼器因初始费用及减振效率不同,生命周期费用也不相同。一般而言,含TLCD装置生命周期费用较含TMD装置减少很多,然而体积却大很多,所占空间大,这对超高层建筑结构空间要求高。含CTD装置生命周期费用介于TMD与TLCD之间,是个很有竞争性的选择。 由于人的主观感受和经济因素具有很强的变异性,精确评估因舒适度问题产生的损失是十分困难的。在本方法推广运用之前,还需要大量的数据统计工作,但本方法为解决基于性能的超高层建筑抗风舒适度问题提供了新的思路。 [1] 周云,汪大洋,陈小兵. 基于性能的结构抗风设计理论框架[J]. 防灾减灾工程学报,2009,29(3):244-251. Zhou Yun, Wang Dayang, Chen Xiaobing. Framework on performance-based wind-resistant design theory[J]. Journal of Disaster Prevention and Mitigation Engineering, 2009, 29 (3): 244-251. (in Chinese) [2] Ciampoli M, Petrini F, Augusti G. Performance-based wind engineering: towards a general procedure[J]. Structural Safety, 2011, 33(6): 367-378. [3] Ciampoli M, Petrini F. Performance-based aeolian risk assessment and reduction for tall buildings[J]. Probabilistic Engineering Mechanics, 2012, 28: 75-84. [4] Petrini F, Ciampoli M. Performance-based wind design of tall buildings[J]. Structure and Infrastructure Engineering, 2012, 8(10): 954-966. [5] Sarja A. Integrated life cycle design of structures [M]. Florida,US:CRC Press,2002:160. [6] Frangopol D M, Liu M. Maintenance and management of civil infrastructure based on condition, safety, optimization, and life-cycle cost [J]. Structure and Infrastructure Engineering, 2007, 3(1): 29-41. [7] 卜国雄,谭平,周福霖. 基于投资-效益准则的TMD装置的优化设计[J]. 土木工程学报,2011,44(5):24-31. Bu Guoxiong, Tan Ping, Zhou Fulin. Optimal design of the TMD device based on cost-effectiveness criterion[J]. China Civil Engineering Journal, 2011, 44(5): 24-31.(in Chinese) [8] 赵昕,余天意. 基于风振舒适度的高层建筑生命周期费用模型[J].同济大学学报:自然科学版,2013,41(12):1793-1798. Zhao Xin, Yu Tianyi. Human Comfort performance-based life cycle cost model of high-rise structures under wind load[J]. Journal of Tongji University:Natural Science, 2013, 41(12): 1793-1798. (in Chinese) [9] Aruitectural Institute of Japan. Guidelines for the evaluation of habitability to building vibration[S]. Tokyo:AIJ Press, 2004. [10] 同济大学建筑设计研究院(集团)有限公司.超高层建筑混合风振控制系统:中国,ZL201420553346.X [P]. 2015-01-14. [11] Griffin M J, Whitham E M. Individual variability and its effect on subjective and biodynamic response to whole-body vibration[J]. Journal of Sound and Vibration, 1978, 58(2):239-250. [12] 曹宏,李秋胜,李桂青,等. 抗风结构安全度的计算方法[J]. 土木工程学报,1994,27(1): 40-48. Cao Hong, Li Qiusheng, Li Guiqing, et al. Calculation of wind-resistant structure safety[J]. China Civil Engineering Journal, 1994, 27(1): 40-48. (in Chinese) [13] 罗乃东,赵国藩. 高层、高耸结构抗风动力可靠度[J]. 大连理工大学学报,2002,42(2):208-212. Luo Naidong, Zhao Guofan. Analysis of dynamic reliability for wind loading of high-rise building[J]. Journal of Dalian University of Technology, 2002, 42(2): 208-212. (in Chinese) [14] Blair A N, Ayyub B M, Bender W J. Fuzzy stochastic risk-based decision analysis with the mobile offshore base as a case study[J]. Marine Structures, 2001, 14(1): 69-88. [15] 瞿伟廉,陶牟华,Chang C C. 五种被动动力减振器对高层建筑脉动风振反应控制的实用设计方法[J]. 建筑结构学报, 2004,22 (2):29-34. Qu Weilian, Tao Muhua, Chang C C. Practical design method for effect of five kinds of passive dynamic absorbers on fluctuation wind-induced vibration response control of tall buildings[J]. Journal of Building Structures, 2004, 22 (2): 29-34. (in Chinese) [16] 谭平,卜国雄,周福霖.带限位TMD的抗风动力可靠度研究[J]. 振动与冲击,2009,28(6):42-45. Tan Ping, Bu Guoxiong, Zhou Fulin. Study on wind-resistant dynamic reliability of TMD with limited spacing [J].Journal of Vibration and Shock, 2009, 28(6): 42-45. (in Chinese) [17] Vanmarcke E H. On measures of reliability in narrow band random vibration[R].[S.l.]:Department of Civil Engineering,Massachusetts Institute of Technology,1969. [18] 刘彬,丁桦,时忠民. 基于柔度修正的局部刚体化结构动力模型简化方法[J].工程力学,2007,24(10):25-29. Liu Bin, Ding Hua, Shi Zhongmin. A model reduction method for dynamic analysis based on quasi-rigid-body mode and flexibility modification[J]. Engineering Mechanics, 2007, 24(10): 25-29. (in Chinese) [19] 王立林,超高结构组合调谐风振控制系统优化设计[D]. 上海:同济大学,2016. 上海市优秀技术带头人计划资助项目(14XD1423900);上海市科技攻关计划资助项目(09dz1207704) 2015-06-27; 2015-09-09 TU972; TH69 赵昕,男,1975年10月生,博士、教授级高级工程师。主要研究方向为高性能结构系统设计、控制与优化。曾发表《超高层建筑结构组合调谐风振控制系统》 (《同济大学学报:自然科学版》2016年第44卷第4期)等论文。 E-mail:22zx@tjadri.com 王立林,男,1991年6月生,博士生。主要研究方向为风振控制及风能控制。 E-mail:lilin.wang@bridge.t.u-tokyo.ac.jp
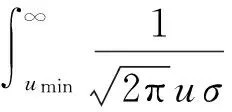

1.3 抗风结构舒适度性能失效费用估算
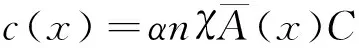

1.4 生命周期舒适度费用评估模型

2 含阻尼器结构生命周期费用评估模型
2.1 风振控制原理


2.2 阻尼器抗风动力可靠度

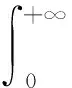
2.3 含阻尼器结构生命周期费用模型

3 基于生命周期费用模型的优化设计分析
3.1 优化设计原理

3.2 优化设计流程
4 算 例

Fig.3 A super tall building model4.1 考虑TMD失效的结构舒适度性能



4.2 基于生命周期费用的优化设计


4.3 结构舒适度性能水平校核

5 结束语

