基于分布函数的潜艇目标强度统计建模

孙乃葳,李建辰,万亚民

(中国船舶重工集团公司 第705研究所,陕西 西安,710077)

基于分布函数的潜艇目标强度统计建模

孙乃葳,李建辰,万亚民

(中国船舶重工集团公司 第705研究所,陕西 西安,710077)

为弥补潜艇目标强度确定性预报模型的不足,开展了标准潜艇的目标强度统计建模研究,以更好地满足实际工程应用的要求。建立基于Parzen窗估计的目标强度密度函数模型; 为获得该密度函数模型统一、简洁的表达式,分别基于常用的分布函数模型对目标强度分布的估计结果进行最优拟合; 并对χ2分布模型进行改进,得到χ2三参数分布模型。通过误差比较可知,改进的χ2三参数分布模型可较好地描述潜艇目标强度分布特征,所建立的统计建模方法及得到的模型参数可为潜艇目标的仿真提供参考。

标准潜艇; 目标强度; 统计建模;χ2分布

0 引言

潜艇由于隐蔽性好且作战效能高,因而备受各国海军青睐。获取潜艇目标强度特性是主动声呐探测的关键技术之一,准确掌握目标在不同态势下的声呐目标强度,对鱼雷等水中兵器的目标检测和参数估计具有十分重要的意义[1]。在鱼雷主动声呐探测潜艇时,由于潜艇目标不仅形体复杂,其在水下运动时与鱼雷的相对空间位置关系也会不断变化,这些都会造成鱼雷寻的脉冲回波特性的改变,导致潜艇回波起伏,进而引起目标强度的时变并影响鱼雷自导检测结果[2]。而目前较为成熟的潜艇目标强度预报模型多是确定性模型,其预报结果不能完全反映水下真实目标强度的起伏特性,因而难以满足实际工程应用要求。

考虑到确定性模型的不足,采用统计建模的方法来描述和预测起伏特性十分必要。国内外对潜艇目标强度的统计建模研究较少,多是在雷达散射截面(radar cross section,RCS)的起伏统计特性研究的基础上开展的。RCS随飞机的姿态及状态变化呈现剧烈的起伏特性,是衡量飞机隐身性能的基本指标,而已有的研究工作多从统计分析的角度去描述和分析 RCS起伏模型[3]。Marcum和Swerlingl最早提出了用于描述RCS起伏统计特性的模型,分别称为 Marcum模型和 Swerlingl-4模型[4],Meyer提出了χ2模型,Heidbreder和Mitchell提出了对数正态模型,Scholefield提出了赖斯模型[5]。陈世春等开展了隐形飞机目标的RCS起伏特性研究[6],以 6种典型隐身飞机 F-117A、B-2、F-35A、X-45A、X-46和 X-47B为研究对象,通过RCS高频计算方法获取了各机型不同入射条件下的散射统计数据,利用χ2模型、对数正态模型和勒让德多项式模型等3种较新的统计模型对计算数据进行拟合,分析研究了各模型拟合的优劣及主要影响因素,得出基本的拟合效果判别方法,该工作为分析计算隐身飞机的雷达检测概率提供了支撑。

近年来,国内将声呐散射原理与雷达散射原理结合,开展了对水下目标强度的统计特性研究,取得了一些成果。上海交通大学结合雷达散射面积起伏机理,将雷达散射面积的概念延伸到水声领域,首次提出了声呐散射面积(sonar cross section,SCS)的概念,借鉴 RCS统计模型建立面向任意目标的SCS起伏统计模型[7]。在此基础上从统计意义上对目标强度进行分析,推导出潜艇的目标强度统计模型并获得了目标强度起伏的统计参数。这是国内首次在水声领域对目标强度统计模型开展的研究,弥补了以往目标强度预报模型是确定性模型的不足,预报结果在一定程度上反映了目标强度的随机性和起伏性,提高了模型在实际工程应用和实验数据分析中的准确性。

文章在前人研究的基础上开展潜艇目标强度统计建模的研究。首先建立基于Parzen窗估计的潜艇目标强度统计模型,然后分别利用χ2分布、对数正态分布、伽马分布以及改进后χ2三参数分布模型对统计模型进行最优拟合,通过相对熵的误差比较,得到了最优的分布函数模型及参数。文中提出的建模方法及模型参数可以更好地用于标准潜艇目标强度统计特性的描述。

1 目标强度分布的Parzen窗估计

基于板块元理论计算可以得到潜艇目标强度理论样本值,然后对目标强度的分布进行核密度估计,该方法属于非参数的估计方法: 对已知的密度函数,在观测点上平均化,以期得到光滑的估计曲线[8]。

假设样本数据值在D维空间服从一个未知的概率密度函数,则其在区域R内的概率为

假设N个样本数据点有K个落入了区域R,则应服从二项分布

由概率知识可知,在样本数N足够大时有

设V为区域R的空间,当区域R足够小时有

将式(3)与式(4)结合可得

根据式(5)来估算密度函数p（x）。假定区域R不变,即V不变,通过决定K的大小来估算密度函数,采用核密度估计方法,可得密度函数为[9]

式中:V=hD,D为数据维数,h为区域V的超立方体的棱长;k取正态分布形式的最优窗函数,其宽度为样本数据范围的 100等分,这种密度函数估计的方法称为Parzen窗估计法。该方法的实质是用正态分布窗函数代替样本值来估计整体的概率密度分布。

采用Parzen窗估计方法对目标强度样本数据进行估计,可得到分布密度函数,分析可知该函数为非线性函数。为找到一种简洁且通用的模型对潜艇目标强度统计分布规律进行描述,从概率分布函数模型出发,采用非线性最小二乘拟合的方法对Parzen窗估计的密度函数进行最优拟合。

2 分布函数误差评价标准

为获得拟合效果最佳的分布函数模型,需要就分布函数对Parzen窗估计的密度分布曲线拟合效果进行合理评价。首先对分布曲线的拟合误差评价标准进行讨论,通过参考相关文献资料[10],归纳总结出2种常用的误差计算公式

式中:pi为原始数据的统计概率;为分布统计模型的拟合概率;N为分段区间个数,以上2种定义误差的方法使计算得到的是误差总和,从而导致结果偏大,不利于工程应用,且从物理含义上不能很好描述概率分布曲线间差异。

由文献[11]可知,在概率论或信息论中,KL散度(Kullback-Leibler divergence)又称相对熵(relative entropy),是一种描述2个概率分布差异的方法。如果一个随机变量X的可能取值为,对应的概率为p(X=xi)(i=1,2,…,n),则随机变量X的熵定义为

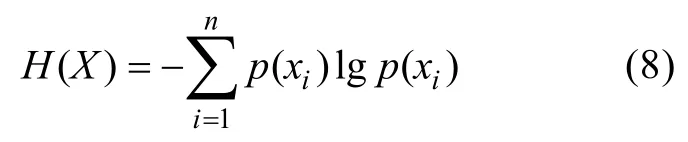
设p(x)和q(x)是X取值的2个概率密度分布,则p对q的相对熵为

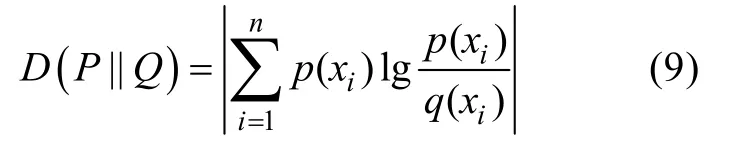
相对熵可以衡量 2个随机分布之间的距离,当2个随机分布相同时,其相对熵为0,当2个随机分布的差别增大时,其相对熵会增大。因此,采用相对熵的评价方法可以较好地对分布函数的拟合效果进行评价。下面分别基于常见概率分布模型对估计得到的密度函数开展建模研究。

3 目标强度分布函数建模

3.1 经典分布函数模型

1) 目标强度Γ分布模型

以χ表示目标强度值,首先给出目标强度Γ分布的概率密度函数

其中,,α β为Γ分布的可变参数。

2) 目标强度对数正态分布模型

若随机变量各个值取对数后服从正态分布,则称该分布为对数正态分布。服从该分布的概率密度函数为

3) 目标强度χ2分布模型

χ2分布适用的目标为大型的、起主导作用的散射体加上大量较小的随机散射体。该分布密度函数表达式为

式中:k为自由度,χ2分布为偏态分布,其分布形态受参数k影响较大。χ2分布为单参量的分布函数,仅与自由度k相关。

3.2 目标强度改进χ2分布模型

结合 3种分布函数的特点,对χ2分布模型的物理意义进行深入研究,以期获得既形式统一,又满足各个舷角建模误差最小的分布模型。查阅相关资料,在飞机雷达反射强度的统计建模中,改进的χ2曲线被广泛应用[12]。这是由于飞机具有直线型结构,机身表面不连续点较多,根据目标的结构特点,选用改进的χ2曲线对飞机 RCS 动态测量数据进行统计建模具有较好的效果[13]。

雷达反射面积的理论分布计算公式为[3]

式中:k为χ2分布模型的自由度数;为雷达的反射截面;为雷达的平均反射截面。其表达式比较简洁,变参数只有 1个,双自由度k可以不是正整数。利用当k=1时为指数分布这一特殊情况,描述由多个独立且具有相同强度的散射体组成的组合体。

考虑到潜艇目标同样具有直线型结构,以及艇身表面不连续点较多等物理结构特征,且应用板块元法计算的潜艇目标强度是由各个独立的小面元的反射强度叠加得到,因此,该改进的χ2分布模型同样适用于潜艇目标强度的统计建模。

综上可知,声呐探测领域目标强度为

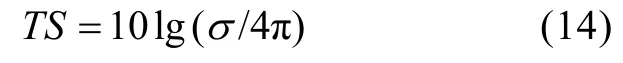
将式(14)和式(15)代入式(13)中,可得

对目标强度求导并令其为0

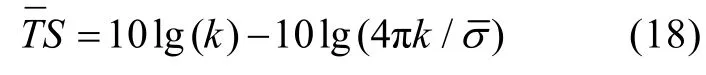
由式(16)得到目标强度的均值

图1 L1与L2对比图Fig. 1 Comparison between L1 and L2

随着k取值的增加,该分布函数所表示的变量均值与峰值所在的变量趋于一致,即分布的期望在概率密度函数峰值附近的目标强度取值。这一结果是符合χ2分布模型在k→∞时接近正态分布模型这一判断。实际计算中,对的估计是基于样本数据值进行的,那么用样本均值估计整体分布的期望可能会存在一定误差,因此,本文引入修正因子,将表示为

可将密度函数用 3个参数c1,c2,c3表示,其中带入上式得

4 模型计算与分析

4.1 Γ 分布函数最优拟合结果

下面采用Γ分布函数分别对艇艏、艇舯和艇艉的目标强度密度函数进行最小二乘拟合,其最优的拟合结果如图2所示。

由图2可知,Γ分布函数由参数,β及x0共同决定,但参数调整对函数形式的影响有限。Γ分布函数可对艇艉的分布函数较好拟合,对艇艏和艇舯的拟合效果较差,尤其是对密度函数两侧拖尾部分拟合效果最差。

4.2 对数正态分布模型最优拟合结果

由图 3可知,对数正态分布模型的拟合效果由σ和μ决定,其对密度函数的拟合效果与Γ分布函数相当,对艇艏、艇舯的拟合较差,同样存在对密度函数拖尾部分拟合效果差的问题。

4.3 χ2分布模型最优拟合结果

由图 4可知,χ2模型拟合效果由自由度k决定,可对艇艏、艇舯和艇艉进行一定程度的拟合,但是受χ2分布函数自身可变参数少的限制,拟合效果相比Γ分布和对数正态分布最差。

由于概率分布模型简单,参数调整对分布曲线的影响受限,以上介绍的 3种典型分布模型对目标强度Parzen窗密度估计的拟合效果均不够理想,采用相对熵的评价方法分别对 3种分布函数的拟合误差进行计算,结果如表1所示。

4.4 改进χ2三参数分布模型最优拟合结果

采用推导得到的χ2三参数分布模型对由Parzen窗估计得到Benchmark潜艇的艇艏、艇舯和艇艉的理论分布函数进行拟合,仿真结果见图5。

图2 典型舷角下Γ 分布的拟合结果Fig. 2 Fitting results of Γ-distribution under typical board angles

图3 典型舷角下对数正态分布拟合结果Fig. 3 Fitting results of log-normal distribution under typical board angles

图4 典型舷角下χ2分布拟合结果Fig. 4 Fitting results of χ2-distribution under typical board angles

图5 典型舷角下χ2三参数分布模型拟合结果Fig. 5 Fitting results of χ2-distribution model with three parameters under typical board angles

表1 分布函数拟合相对熵误差表Table 1 Fitting errors of relative entropy for distribution function

从图2～图4可看出,χ2三参数分布函数对Parzen窗函数的估计效果有很大提高。计算得出χ2三参数分布曲线拟合的参数c3=及与Parzen窗估计相对熵误差D见表2。

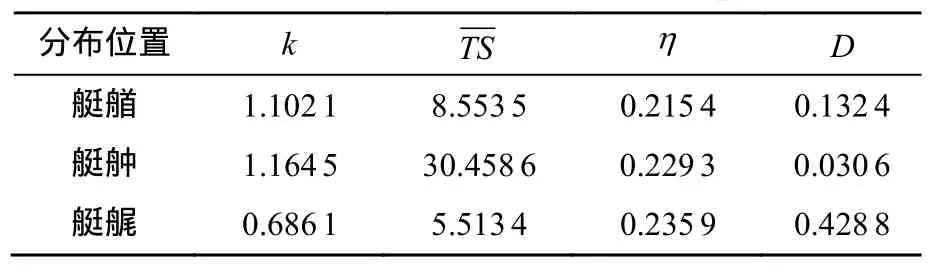
表2 参数及相对熵误差表Table 2 Parameters and relative entropy error

由表 2可以看出,χ2三参数分布模型对潜艇艏部、舯部和艉部的估计密度函数均能较好地拟合,并获得相应的统计参数;χ2三参数分布模型比上文提到的3种分布函数模型的拟合效果都好;采用相对熵误差作为分布曲线拟合度的评价指标时,艏部拟合误差较小,舯部拟合误差次之,艉部的拟合误差最大,评价结果符合实际情况。

5 结束语

文中从统计意义出发,开展标准潜艇的目标强度统计建模研究。建立基于Parzen窗估计的目标强度密度函数模型; 为获得模型统一简洁的表达式,研究了基于分布函数的目标强度统计建模,推导得到用于描述潜艇目标强度的χ2三参数分布模型; 比较基于相对熵的分布误差可知,改进的χ2三参数分布模型能对潜艇目标强度的统计分布特性进行最优描述,相关模型和参数可为自导系统潜艇目标仿真提供参考。文中对潜艇目标强度的统计建模是基于板块元理论的计算样本值得到的,后续研究将结合实验测量数据进一步完善所建模型并修正模型参数。

[1] 刘伯胜,雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社,2009.

[2] 石秀华,王晓娟. 水中兵器概论(鱼雷分册)[M]. 西安:西北工业大学出版社,2010.

[3] 王凯,李侠,蔡万勇,等. 影响军用复杂目标RCS起伏的主要因素分析[J]. 空军雷达学院学报,2012,26(1): 1-3.Wang Kai,Li Xia,Cai Wan-yong,et al. Analysis of Major Factors on RCS Variation of Military Complex Targets[J].Journal of Air Force Radar Academy,2012,26(1): 1-3.

[4] Xu Xiao-jian,Huang Pei-kang. A New RCS Statistical Model of Radar Targets[J]. IEEE Trans. Aerospace and Electronic Systems,1997,33(2): 710-714.

[5] 丁凯,赵红云.一种目标角闪烁统计模型算法及仿真[J].舰船电子工程,2011,31(3): 133-134,161.Ding Kai,Zhao Hong-yun. An Algorithm and Simulation of Angular Glint Statistical Model[J]. Ship Electronic Engineering,2011,31(3): 133-134,161..

[6] 李莹,黄沛霖,武哲. 基于不同角域 RCS均值的雷达探测模型[J]. 北京航空航天大学学报,2008,34(6): 627-629.Li Ying,Huang Pei-lin,Wu Zhe. Model of Radar Network Detection Based on Average RCS Value of Different Angle Territory[J]. Journal of Beijing University of Aeronautics and Astronautics,2008,34(6): 627-629.

[7] 李建龙,王新宁,范军. 潜艇目标强度起伏统计模型[J].声学技术,2014,33(1): 1-5.Li Jian-long,Wang Xin-ning,Fan Jun. A Statistical Fluctuation Model of Submarine Target Strength[J]. Technical Acoustics,2014,33(1): 1-5.

[8] Hall P,Wand M P. On the Accuracy of Binned Kernel Density Estimators[J]. Journal of Multivariate Analysis,1996,56(2): 165-187.

[9] Botev Z I,Grotowski J F,Kroese D P. Kernel Density Estimation via Diffusion[J]. The Annals of Statistics,2010,38(5): 2916-2957.

[10] 胡章芳,郭瑞红. 实验数据处理方法的探讨[J]. 重庆邮电学院学报(社会科学版),2004(z1): 151-153.Hu Zhang-fang,Guo Rui-hong. Discussion on the Methods of Experimental Data Processing[J]. Journal of Chongqing University of Post and Telecommunication (Social Sciences Edition),2004(z1): 151-153.

[11] 桂现才. 基于相对熵的一种属性约简算法[J]. 计算机工程与应用,2006,42(33): 197-199.Gui Xian-cai. Attribute Reduction Algorithm Based on the Relative Entropy[J]. Computer Engineering and Applications,2006,42(33): 197-199.

[12] 庄钊文,袁乃昌. 军用目标雷达散射截面预估与测量[M]. 北京: 科学出版社,2007.

[13] 李琦,薛凯,李慧宇,等. 太赫兹雷达散射界面测量研究进展[J]. 激光与光电子学进展,2012,49(6): 1-8.Li Qi,Xue Kai,Li Hui-yu,et al. Advances in Research of Terahertz Radar Cross Section Measurements[J]. Laser &Optoelectronics Progress,2012,49(6): 1-8.

Statistical Modeling of Submarine Target Strength Based on Distribution Function

SUN Nai-wei,LI Jian-chen,WAN Ya-min
(The 705 Research Institute,China Shipbuilding Industry Corporation,Xi′an 710077,China)

Statistical modeling of benchmark submarine target strength(TS) is performed to cover the shortage of deterministic forecast model. A TS density function model is established by Parzen window estimation. Then to get an unified and succinct expression of the density function model,typical distribution function models are used for optimal fitting of TS estimation. Ultimately an improvedχ2distribution model with three parameters is established. Errors comparison indicates that this improvedχ2-distribution model can describe the submarine TS reasonably. This study may provide a reference for submarine target simulation.

benchmark submarine; target strength; statistical modeling;χ2-distribution

TJ630.2; TB112

A

2096-3920(2017)03-0256-06

孙乃葳,李建辰,万亚民. 基于分布函数的潜艇目标强度统计建模[J]. 水下无人系统学报,2017,25(3): 256-261.

10.11993/j.issn.2096-3920.2017.03.007

2017-03-22;

2017-04-19.

孙乃葳(1993-),男,硕士,主要研究方向潜艇目标特性.

(责任编辑: 陈 曦)