一种基于粒子群优化(PSO)算法的全局快速终端滑模控制方法
2017-11-03郝春玲
郝春玲
(渤海船舶职业学院机电工程系,辽宁 葫芦岛 125100)
一种基于粒子群优化(PSO)算法的全局快速终端滑模控制方法
郝春玲*
(渤海船舶职业学院机电工程系,辽宁 葫芦岛 125100)
为了减小六轴机械臂运行时的震动,提高控制系统的响应时间,基于PSO智能算法对其进行全局优化控制,将机械臂系统离散成6个子系统,分别设计各个子系统,并且基于Lyapunov理论验证控制系统的稳定性。仿真结果表明,采用PSO算法对六轴机械臂进行运行轨迹控制时具有精度高、运行误差小及收敛周期短的优点,切实提高了控制系统的响应速度及控制精度。
智能机器人;PSO算法;六轴机械臂;终端滑模控制
随着科技的不断进步,以及时下较为流行的工业4.0,机器人逐渐体现了其特有的优势,对其进行智能控制成为了国内外学者的研究热点,文献[1-3]阐述了基于模糊控制策略调整PID值,表现出了较好的鲁棒性。由于机器人的动作具有时空上的非线性,各类因素间具有极强的耦合性等特性,以及内部与外部的各类影响因素对其产生了较大的干扰,影响了其控制精度以及相应速度。文献[4-6]提出基于滑模控制来对具有极强非线性的各类系统均具有较优异的控制性能。近年来,滑模控制被应用于各行各业,均表现出了较为优异的性能,其主要是基于通过采集的各类输入因素实际值来进行具体的反馈控制,使得输出值与实际需要的控制变量得到较好的符合度。文献[7-8]基于二阶滑模算法对具有3个自由度的机器人进行运行轨迹控制,并与传统PID控制算法作了对比分析。文献[9]基于非线性的滑模算法对机器人进行非线性控制,大幅提高了其控制精度。
文献[10-12]基于自适应滑模模糊控制算法以及更高阶的算法对机械手臂进行智能控制,具有较好的鲁棒性。但是,此类算法即使能够提高控制鲁棒性,但其在控制过程中需要循环往复的切换,导致被控系统出现较大的抖动,造成了跟踪误差的大幅增加。对于工业机器人的应用中,轨迹跟踪出现较大误差时,会导致整个系统的精确度受到较大的影响。对于此问题,衍生出较多新的控制算法,如将人工智能神经网络算法进行改进,可大幅减小系统震动所产生的误差。
综上,为了进一步提升控制系统的响应速度以及大幅降低被控系统的振动,基于一种粒子群算法对六自由度的机械手进行全局滑模控制,并得到了系统的响应时间,仿真结果经过实验数据验证了其具有较高的精度。
1 控制系统建模
1.1 数学模型
机械臂刚体的线加速度[13]
(1)
机械臂刚体的角加速度为:
vA=UVAORG
(2)
惯性张量如式(3):
(3)
ωA=UΩA
(4)
关节计算力矩如下:
(5)
Ixx=∭v(y2+z2)ρdv
(6)
Iyy=∭v(x2+z2)ρdv
(7)
Izz=∭v(x2+y2)ρdv
(8)
Ixy=∭vxyρdv
(9)
Ixz=∭vxzρdv
(10)
Iyz=∭vyzρdv
(11)
旋转关节的计算公式为:
(12)
移动关节公式为:
(13)
机械臂动力学方程的结构状态空间方程为:

(14)
形位空间方程表达式为:
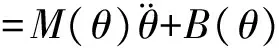
(15)
笛卡尔状态空间方程为:
(16)
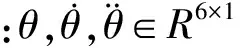
1.2 滑模控制器设计
设单关节的常规全局快速终端滑模控制器的滑模面函数如下:
(17)
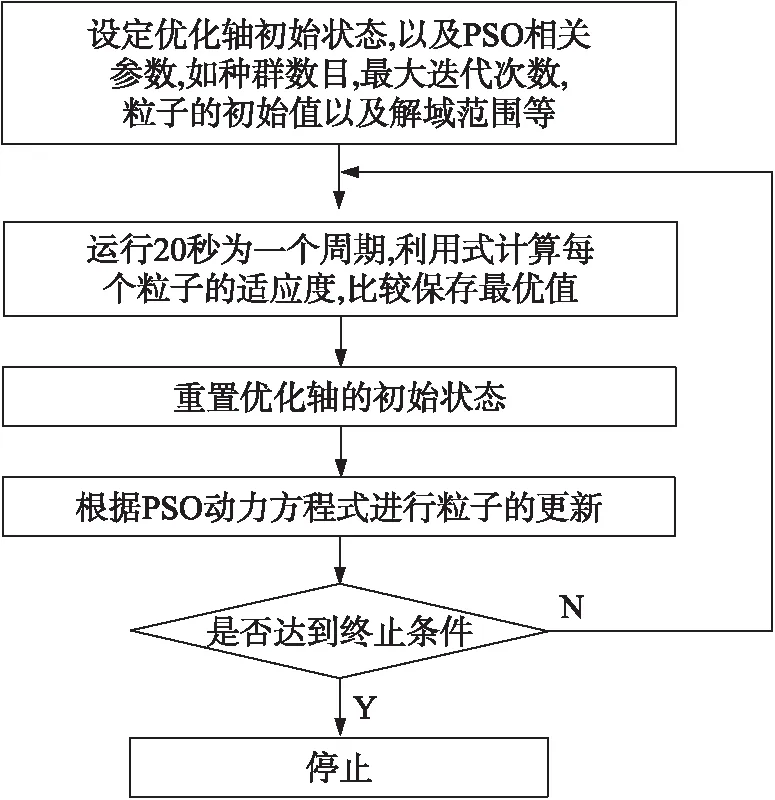
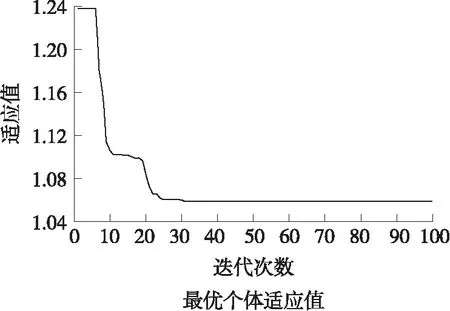
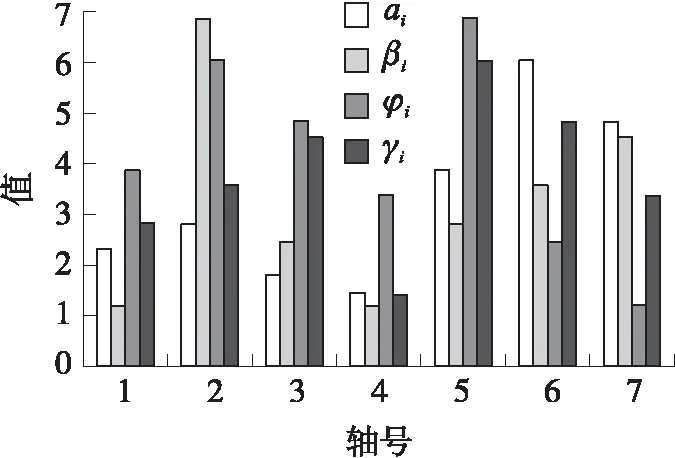
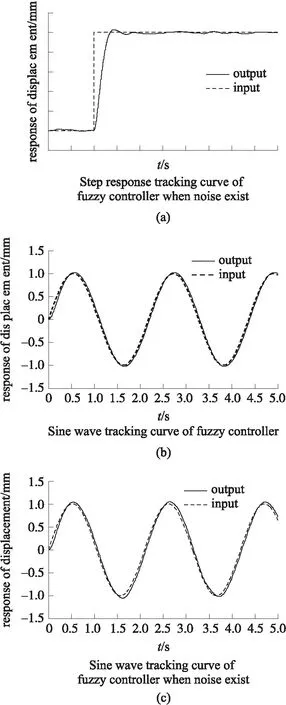
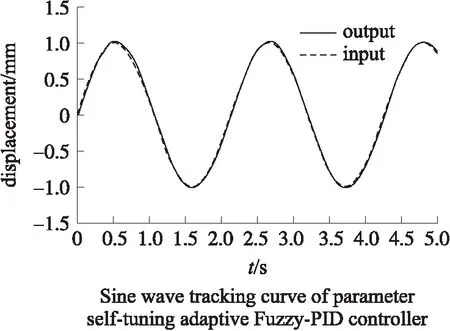
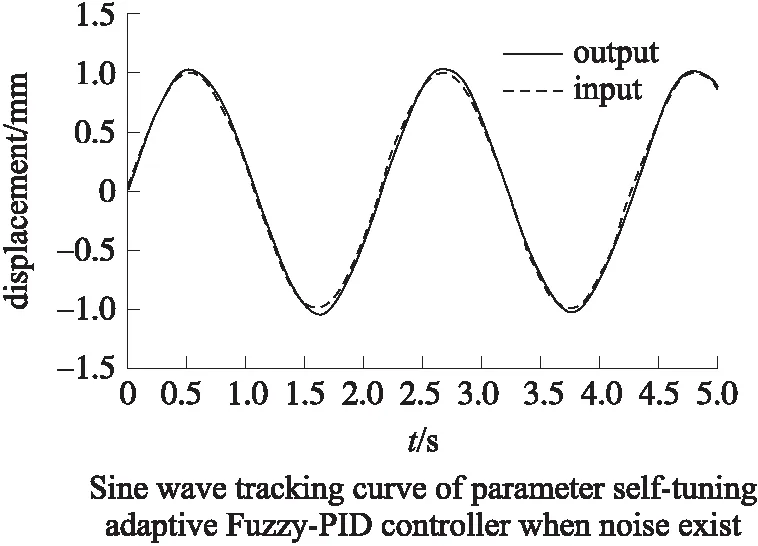
式中:Q (18) 定义Lyaounov函数: (19) (20) 本文3个通道均为二阶系统,则得控制器为: (21) 此时可以根据 (22) (23) 算出收敛时间ts以及到达滑模面的时间tsn-1。 其中,一种具有递归结构的快速滑动模态表示为: (24) 式中:ai,βi>0,Pi,Qi(Pi>Qi) (i=0,1,…,n-2)为正奇数。 基于PSO算法[14-15]对机械臂进行滑模优化控制步骤如下: 假设种群大小N=3,在搜索空间中随机初始化每个解的速度和位置,计算适应函数值,并且得到粒子的历史最优位置和群体的全局最优位置。 gBest=pBest1=(-5,9) (25) 步骤2:粒子速度以及位置的更新 (26) 式中:w是惯量权重,一般取[0,1]区间的数,这里假设为0.5,c1,c2为加速系数,取2.0,r1,r2为[0,1]区间上的随机数。 在Simulink环境下建立的模型如图2所示,图2中,微分环节由一个一阶环节近似,输出端口1即为式(2)所示的ITAE指标,通过将时间及误差绝对值的乘积进行积分后得到。 3.1 仿真研究 基于六自由度实验台的实测数据验证本文所提动力学模型及控制算法的精确度,如图1所示,基于全局终端快速滑模算法对各个关节进行粒子群算法仿真计算。 图1 基于PSO优化的全局快速终端滑模系统 确定优化结果范围,由上述模型可知,系统运行达到平衡时所需时间为t=ts+tr;由上述分析可知增大αi,βi的值,可提升控制系统的响应速度,但是其过快的响应速度会导致被控机械臂运行时发生较大的震动,此时可通过调节其βi,φi来对机械臂的震动的幅度加以控制与调节,基于机械臂自身所具有的力学性能,将其控制输出量设置为τi∈[-10,10]N·m。为了选取最为合适的输出控制范围,将其范围设定在[0,10]之间,粒子群算法的粒子数为25个,设定其最大迭代次数为100。采取单轴单次优化的模拟方法对机械臂进行优化计算,并且将其他轴设置为0,将机械臂逐步进行优化计算之后,停止。 经过图2的仿真过程以后,六轴机械臂运行优化计算结果如图4所示,图4表明机械臂运行仿真经过十次迭代呈现出收敛趋势。 图2 仿真计算流程 图3 轴1优化函数曲线 图4 PSO优化滑模参数 当仿真计算过程经过精度判断达到停止条件后,最终得到六轴机械臂的最优运行轨迹参数。 3.2 实验研究 本次实验是基于Googol公司生产的,数据采集周期为0.002 s/次,此类控制系统可与各类型PLC进行连接,此联合工作可大幅提升控制精度以及响应速度,可与DSP技术完美接口,实验系统实物如图5所示。 图5 CPAC硬件结构图 图6 基于PSO优化全局快速终端滑模实验结果 图6表明了实测数据结果,基于本文所提的控制算法对六轴机械臂进行终端全局滑模运行控制时表现出了较快的响应速度,避免了六轴机械臂系统在运行时出现系统超负荷调节的不良现象,从而减小了六轴机械臂运行时产生较大的摩擦,造成不可逆的损坏,针对机械臂处于稳态运行时,其输入与输出值均表现出了良好的性能。 实测值与设定值符合度较好,经过仿真优化以后的误差范围控制在1°~4°之间,由此可以得到本文所提算法具有控制响应速度快,超调几率小以及系统运行轨迹精度较高的优势。 图7、图8均表明了本文所提控制算法的输入输出值均表现出了优异的性能,实测值与设定值符合度较好,在系统各个轴有输出力矩时,经过优化以后的控制系统具有较好的控制性能,并且可以快速进行切换,因此,本文所提控制算法对于六轴机械臂运行轨迹的运行精度具有较为准确的定位精度,在应用机械臂进行工业生产操作时,具有较高的精度。 图7 各关节控制器输入输出值 图8 各关节控制器输入输出值 本文对六轴机械臂在工业生产过程中精确控制提出了基于机械臂自身特性,离散成6个被控子系统,采用全局滑模终端控制对其进行精确运行控制,验证了采用粒子群算法对六轴机械臂进行运行轨迹控制时具有较高的精度,具有较短的系统提升试件,运行误差较小以及控制系统收敛周期较小的优点,切实提高控制系统的响应速度及控制精度。 [1] Ott E,Grebogi C,Yorke J. Controlling Chaos[J]. Physical Review Letters,2012,64(11):1196-1199. [2] Pecora L M,Carroll T L. Synchronization in Chaotic Systems[J]. Physical Review Letters,2013,64(8):821-824. [3] Bogris A,Argyris A,Syvridis D. Encryption Efficiency Analysis of Chaotic Communication Systems Based on Photonic Integrated Chaotic Circuits[J]. IEEE J of Quantum Electronics,2012,46(10):1421-1429. [4] Wang L P,Liu W,Shi H. Noisy Chaotic Neural Networks with Variable Thresholds for the Frequency Assignment Problem in Satellite Communications[J]. IEEE Trans on Systems,Man,and Cybernetics—Part C:Applications and Reviews,2014,38(2):209-217. [5] Buscarino A,Fortuna L,Frasca M,et al. Design of Time-Delay Chaotic Electronic Circuits[J]. IEEE Trans on Circuits and Systems—Ⅰ:Regular Papers,2011,58(8):1888-1896. [6] Zhang H G,Ma T D,Huang G B,et al. Robust Global Exponential Synchronization of Uncertain Chaotic Delayed Neural Networks via Dual-Stage Impulsive Control[J]. IEEE Trans on Systems,Man,and Cybernetics—Part B:Cybernetics,2015,40(3):831-844. [7] Moez F. Sliding Mode Control and Synchronization of Chaotic Systems with Parametric Uncertainties[J]. Chaos,Solutions and Fractals,2016,41(3):1390-1440. [8] Hornik K,Stinchcombe M,White H. Multilayer Feed Forward Networks are Universal Approximates[J]. Neural Networks,1989,2(5):359-366. [9] Huang M Z,Ma Y W,Wan J Q,et al. Simulation of a Paper Mill Wastewater Treatment Using a Fuzzy Neural Network[J]. Expert Systems with Applications,2012,36(3):5064-5070. [10] Furuta K. Sliding Mode Control of a Discrete System[J]. Systems and Control Letters,1990,14(2):145-152. [11] Lu T C,Lee C C,Hisa W Y. Supporting Large-Scale Distributed Simulation Using HLA[J]. ACM Transactions on Modeling and Computer Simulation,2013,10(3):268-294. [12] Boukerche A,Hoy A,Thomas N. Dynamic Grid-Based Multicast Group Assignment in Data Distribution Management[C]//International Workshop on Distributed Simulation and Real-Time Applications. SanFrancisco:IEEE,2012:108-115. [13] 钱雪平,赵沁平. 基于关联空间的数据过滤方法[J]. 计算机学报,2012,25(7):723-729. [14] 王君洪,陈跃东,陈孟元. 基于模糊认知图的智能配电网WSNs实时性与可靠性优化研究[J]. 传感技术学报,2016,29(2):214-215. [15] 汤辰,万衡. 基于服务机器人的人体追踪技术的研究[J]. 电子器件,2015,38(6):1398-1399. AGlobalFastTerminalSlidingModeControlMethodBasedonParticleSwarmOptimizationAlgorithm HAOChunling* (School of Mechanical and Electrical Engineering,Bohai Shipbuilding Vocational College,Huludao Liaoning 125100,China) In order to eliminate the chattering and improve the response speed of the system. This paper deals with a fast terminal sliding mode control method based on PSO(particle swarm optimization)for the six manipulator control system. Then stability of the system is demonstrated by Lyapunov theory and the optimization control parameters are achieved based on PSO algorithm. The simulation results show that the PSO algorithm has the advantages of high precision,low running error and short convergence period when the trajectory control of the six-axis manipulator is carried out,thus the response speed and control precision of the control system are all improved. intelligent robot;PSO;6-DOF manipulator;global fast terminal sliding mode 10.3969/j.issn.1005-9490.2017.05.048 2016-07-22修改日期2016-11-03 TP24 A 1005-9490(2017)05-1304-05 郝春玲(1978-),女,黑龙江人,汉族,大学本科,工程硕士,副教授,研究方向为机械自动化,gouchezx@163.com。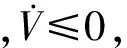
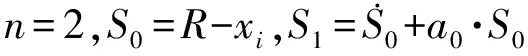
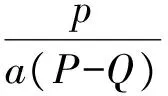
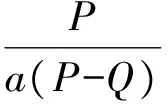
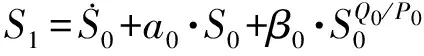
2 PSO优化机械臂滑模控制系统


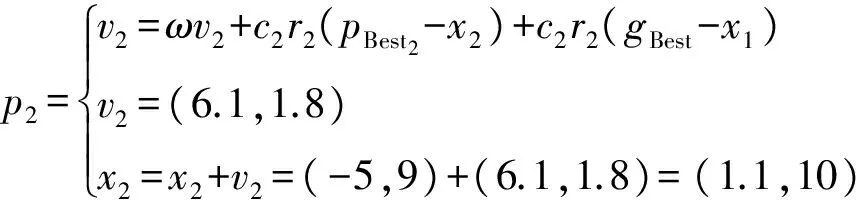
3 仿真及实验结果


4 结束语

