一种基于参数提取算法的快速ADC测试方法*

2017-11-03王逢州

电子器件 2017年5期

关键词：点数直方图静态

陈豹,王逢州

(徐州工程学院信电工程学院,江苏徐州 221000)

一种基于参数提取算法的快速ADC测试方法*

陈豹*,王逢州

(徐州工程学院信电工程学院,江苏徐州 221000)

对于传统的ADC测试方法,若要得到动、静态性能指标,需通过两次测试测得,所需时间较长。文章首先采用移动平均滤波器对静态测试时的直方图算法进行时间优化,然后对静态测试采集的测试点进行抽取,并消除增益误差后,基于参数提取算法通过傅里叶变化得到所有的ADC动态参数。实验结果表明,文章所提算法所得的最大INL估算误差为0.186 LSB,SINAD、ENOB、THD、SFDR估算误差分别为 0.211 dB、0.035、0.159 dB、0.119 dB。与原估算算法相比,优化算法所得SINAD和ENOB的估算精度提高了0.411 dB和0.057。与传统ADC测试方法相比,在保证测试精度的前提下,测试时间减少了50.769%。

ADC测试;测试估算;参数提取;移动平均滤波

模数转化器(A/D转换器或者ADC)作为将连续的模拟信号转换为计算机可以处理的数字信号器件,即现实世界与机器语言之间的重要接口,已经成为现代电子系统中不可或缺的重要组成部分[1]。为了满足更高层次的应用需求,ADC芯片的集成度以及内部复杂度不断提高,这就需要更高效、可靠的ADC测试方法对芯片进行性能测试以保证芯片的稳定性应用。

ADC主要有两类性能指标。一类是基于ADC转移特性曲线命名,包括积分非线性(INL)、微分非线性(DNL)、偏移误差(Offset Error)以及增益误差(Gain Grror)[2]。根据IEEE标准,这些参数主要是利用正弦信号或斜坡信号作为输入信号,用直方图方法获得[3]。另一类性能指标是ADC的频谱性能,主要包括总谐波失真(THD),无杂散动态范围(SFDR)、信噪比(SNR)等。这些参数主要是利用高纯度的正弦信号作为输入信号源,用快速傅里叶变换(FFT)方法测得[4]。在国际上,关于ADC芯片测试方面的报道很多。针对传统测试方法,即直方图测试以及动态测试算法,国际上制定了许多测试标准为ADC测试提供参考。例如IEEE Std.142—2000[5],IEC Std.1057—2007[6]等。根据传统的测试方法,若要测得A/D转换器的所有性能指标往往需要两次测试过程。

通过研究ADC静态参数与动态参数之前的关系,仅通过一次静态测试或者一次动态测试过程获得ADC所有性能参数是降低ADC测试成本的主要方法之一[7]。有很多文章提出利用动态测试方法通过估算得到积分非线性曲线[8-10],能够避免进行静态测试过程以较少测试成本。但是,由于动态测试所需采样点少,这些方法只能粗略的描绘积分非线性曲线,与传统直方图测试方法相比,存在精度低等问题[11-12]。另外一些学者研究基于静态测试估算动态参数的估算方法。由于此类方法基于静态测试过程,能够利用大量的采样点数精确的得到静态参数和动态参数值,达到了一次测试过程测得所有性能参数的目的,减少了动态测试过程所需成本。

目前用静态测试估算动态参数的方法主要有两大类。一类是通过静态测试估算总噪声功率,进而通过计算求出信纳比和有效位数:文献[11]提出利用正弦直方图测试所得的实际ADC转移特性曲线与理想转移特性曲线之差,计算并推导噪声功率公式,进而计算出信纳比以及有效位数;文献[12]提出利用正弦直方图测试所得的积分非线性误差值,通过研究积分非线性与谐波的对应关系建立噪声功率与积分非线性误差值之间的关系表达式,从而计算得到信纳比和有效位数值;文献[13]提出利用微分非线性误差估算总噪声功率。此算法主要是利用斜坡直方图方法所得的微分非线性误差值,通过分析微分非线性误差所包含的噪声成分并进行一系列数学运算得到噪声功率值,从而得到信纳比以及有效位数值。

基于静态测试估算动态参数方法的另一类研究主要是通过估算研究得到无杂散动态范围以及谐波失真参数。由于ADC动态参数性能参数中无杂散动态范围和总谐波失真参数能够反映出ADC谐波以及杂散的情况,所以它们是ADC关键的性能参数。但是,在之前的研究中并未通过估算方法得到这些参数指标。因此,2012年Jingbo Duan[14]和Le Jin等人提出利用斜坡直方图方法所得的积分非线性曲线,通过对曲线进行建模,并用理想的正弦波对其进行采样,以此得到能够进行傅里叶变换的积分非线性曲线。利用积分非线性与谐波之间的关系,通过对重组后的积分非线性曲线进行频谱分析,以此得到无杂散动态范围以及总谐波失真参数指标。

通过国外学者对动态参数估算算法的研究可以发现,这些估算算法只能计算得到一部分动态参数指标,并不能得到全部动态参数指标,使得测试算法具有一定的局限性。而且,这些方法根据积分非线性、微分非线性或者是转移特性曲线通过不同的估算方法来计算动态参数值,为了估算准确需要精确的直方图测试结果,使得测试时间大大增加。因此,需要进一步的研究动态参数估算算法,对原算法存在的缺点进行优化,以达到减少测试成本的目的。文章所提出的参数提取测试算法,不需要进行直方图测试,仅需要采集静态测试所需的数字码,不需要大量采样点数的情况下保证了测试精度,并减小了测试时间,而且所提方法通过实际频谱图得出噪声功率,并非将理想量化噪声功率作为噪声,所得计算结果精确。

文章的主要内容安排如下:第1节主要介绍改进算法的实现过程;第2节主要介绍改进算法的仿真结果;第3节说明测试结果;第4节总结全文。

1 基于参数提取的快速ADC测试算法

1.1 算法原理

对于理想ADC,其输出数字码中仅包含量化误差,所以理想ADC的转换特性可由式(1)所示。

Vin(k)=C(k)+Q(k),k=0,…,2bits-1

(1)

在实际ADC测试中,由于器件内部以及测试电路中噪声和非线性的存在,其实际的传输函数表达式如式(2)。

(2)

式中:Vin为输入信号,n为测试系统存在的噪声,C(k)为ADC输出码值,offset为偏移误差,gain为增益误差,Q为量化误差,k为输出数字码,k=0,…,2n-1,bits为ADC位数。根据式(2),若对测试所得输出码进行傅里叶变换,可得:

(3)

(4)

式(3)中:FFT[Ck]即对实际ADC输出码值进行FFT测试,其结果包含等式右面几项,FFT(Vin(k))正弦波输入信号的傅里叶表达式,在频谱中体现在基波分量上,即输入信号频率fin对应的谱线。FFT(offset)代表直流偏移,即当频率为0 Hz对应的谱线。FFT(INL(k))对应于频谱的谐波分量,FFT(Q(k))对应于频谱中的噪底以及谐波分量。

由以上分析可知,静态测试输出数字码中包含动态参数信息,并且可以通过频谱分析计算得出。故,设计提出利用静态测试所得的输出字码,通过数据分析与处理后,计算得出动态参数。这样就可以不需要进行动态参数测试,仅需一次静态测试,即可计算得出所有性能参数,大大减少了因动态测试所需测试成本以及测试时间。下面详细介绍优化算法的具体实现过程。

1.2 算法实现

设计算法通过以下4个步骤实现,具体测试流程图如图1所示,首先在待测ADC上施加适当的正弦输入信号,并提供满足待测ADC要求的时钟信号,使待测ADC工作在正常工作模式,使用逻辑分析仪采集并存储测试方法所需的输出数字码,最后将该输出数字码传入计算机处理,获得待测ADC的动静态参数。设计算法核心在于基于一次测试后通过参数提取算法获得动态参数和基于改进正弦直方图方法获得静态参数。具体的动态和静态测试过程如图2所示,下面详细阐述算法实现过程。

图1 文章所提方法的具体测试流程图

图2 具体静、动态测试过程

1.2.1 算法的时间优化

采集到的数字码需要同时满足直方图测试和估算动态参数测试是两个过程,这样才能达到一次性测试所有ADC性能参数的目的。因此,在考虑采样点数时应同时考虑这两个测试过程,以得到最优的采样点数。

对于设计算法,只需保证做频谱测试的8 192个点即可精确的估算动态参数。图3给出了在不同采样点数情况下的动态参数测试误差曲线,从图中可以看出,随着采样点数的增加,测试误差并没有减少,而是在误差允许的范围内波动。因此,对于单纯的频谱测试,8 192个采样点数即可。

图3 不同采样点数的动态参数测试误差曲线

对于正弦直方图测试来说,8 192个点数无法得到正确的性能参数,测试误差高达1 LSB,显然8 192个采样点数是不可以用来求得静态性能参数。但是在ADC数据手册中,一般INL的技术参数只关心其最大的INL值。为了节省计算时间,文章采用优化的正弦直方图方法计算得到静态参数。优化的正弦直方图即采用移动平均滤波器法,对采样点数少的INL曲线进行处理,拟合得出精确的INL曲线。如式(5)所示。

(5)

分析点数对INL误差的影响发现当采样点数为6.554×104时,即平均每个代码采样16次时,与标准正弦直方图测试的最大INL值仅差0.089 LSB。综上所述可知,当采样点数为平均每个码值采集16次时,即可达到一次测试测得精确的静态参数和动态参数的目的。相比于传统测试以及基于INL参数估算动态参数方法,文章所提方法在确保计算精度的情况下,测试时间能够减少一半以上。下面介绍由采集的ADC输出数字码值估算ADC的动态参数过程。

1.2.2 参数提取

静态测试的目的是求静态参数,比如偏移误差、增益误差以及积分非线性误差。从奈奎斯特采样定律可知,只要满足采样信号频率大于两倍的输入信号频率,就可以恢复出原始输入信号的波形信息。为了让所采集的数字码能够进行FFT测试,需对静态码值进行处理。对于静态测试,即需对一个码值进行多次采样,以进行数理统计操作。但是,对于动态测试来说,并不需要这么多的采样点。因此,为了节省计算时间,在不影响原始波形信息的情况下,需提取出部分码值,然后进行动态参数测试。例如,图4中将静态码值以Code(4)为起点,每隔一个数字码取一点,得到的一组码值可组成由图中的曲线。根据奈奎斯特采样定律可知,只要最后所得的点数足够多,就可以恢复出原始波形信息。

图4 静态码值提取过程

此时恢复出的原始波形并不能直接用于进行动态参数的分析,因为动静态测试中使用的波形增益不同,静态测试中的高增益信号直接用于动态测试会使得动态测试频谱中出现大量的高频谐波从而无法得到ADC真实的动态性能。因此,需要对恢复的波形进行处理,即消除增益误差的影响。

1.2.3 消除增益误差的影响

对于动态测试来说,通常需要非常高精确度的信号源来保证输入信号的幅度在很精确的范围内,即要严格低于ADC满量程幅度。在静态测试时,为了能够将所有码值采集到,其采用的测试条件是输入信号幅度略高于ADC满量程幅度。因此,为了能够从静态的码值提取出正确的谐波失真信息,需对增益误差进行校准,消除这部分对谐波分量的影响,进而估算得出正确的动态参数值。定义bits位ADC,其输入正弦波为:

x(t)=Aactualsin(2πft+φ)+Vos(actual)

(6)

式中:Aactual为实际输入信号幅度,f为输入信号幅度,Vos(actual)为直流偏移。通过静态测试所得的码值,其幅度Aactual大于满量程输入信号幅度。对此输入信号采样N个点后,得到y[n]如:

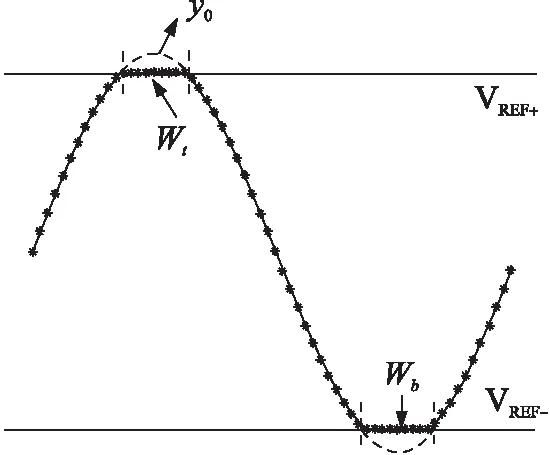
图5 输出信号图

(7)

然后,对y[n]做傅里叶变换,得到Y[k]后,根据傅里叶系数求出y[n]的周期J1和初始相位φ1。J1即为输出频谱中基波所对应的频率分辨率,公式如下:

J1=max1≤k≤N/2{abs(Y(k))}-1

(8)

(9)

在计算得到J1和φ1后,利用最小二乘法求出所求未发生截断的信号y0[n]周期J0和相位φ0为:

J0=ΔJ+J1

(10)

φ0=Δφ+φ1

(11)

式中:ΔJ为J和J1之差,Δφ为φ和φ1之差。最后可拟合得到未发生截断的波形表达式,即增益误差消除后表达式:

(12)

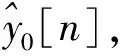
(13)

(14)

最后,将得到的y0[n]进行傅里叶变化即可得到不受幅度影响的频谱图。

1.2.4 计算动态参数

根据步骤2和步骤3的方法获得频谱分析图后,需计算ADC的动态性能参数,各个参数的表达式如下:

(15)

(16)

(17)

(18)

此时通过频谱可以得到ADC的全部动态参数。

2 仿真结果

整体算法仿真文章借助MATLAB(2010b版本)软件作为实验验证工具。在原算法的基础上利用优化的直方图方法,即采用移动平均滤波器法进行计算,实验表明,在采用65 540个采样点数时,得到的最大INL值与标准直方图方法得到的最大INL值仅相差0.089 LSB,如图6所示。

图6 2种方法所得INL曲线

图7 所提算法与标准动态测试算法比较频谱图

根据标准动态FFT测试可知,其最多仅需8 192个采样点数。因此,在仿真中对所采集的数字码进行等间隔提取,最后取得8 192个数据。为了更好验证此算法的准确性,在相同的测试条件下,利用标准动态测试方法,得到频谱图,校准前后的频谱图如图7所示。

3 实验结果

通过12位ADC模型仿真验证改进算法的可行性之后,采用14位实际ADC芯片进行验证,如图8所示。文章采用14位ADC芯片AD9258作为实测芯片,主要完成3个实验验证。通过3组实验来验证所提算法,3组实验分别为原估算算法、文章所提算法以及标准动态测试算法。3种方法测试得到的动态参数的值如表1所示。文章所提算法在确保测试精度的同时,只经过一次采集获得了ADC的所有测试参数,与传统测试方法相比大大节省了测试时间,文章所提方法的测试时间与传统时间相比降低了50.769%。

图8 AD9258测试PCB

标准算法基于INL值估算动态参数算法文章算法SINAD/dB69．72369．16969．934ENOB/bit11．29011．19811．325THD/dB-88．057∗-87．898SFDR/dB-92．473∗-92．354

4 结论

针对当前ADC测试领域出现的问题,文章采用基于参数提取测试算法,文章采用优化的直方图测试,即采用移动平均滤波器对直方图测试进行时间优化,与所提算法相结合的ADC整体测试架构,大大优化了测试时间。对于动态参数的获得,主要是采集静态码值,通过参数提取减少频谱测试所需计算量后,消除增益误差的影响,最后通过傅里叶变化得到全部动态参数。

[1] 吴光林,胡晨,李锐. 一种有效的ADC内建自测试方案[J]. 电子器件,2003,26(2):190-193.

[2] 董振龙,董惠,武锦. 基于FPGA的高速 ADC测试平台的设计[J]. 计算机测量与控制,2012,20(9):2372-2374.

[3] 黄远望,严济鸿达,周伟. 基于FPGA的数据采集测试系统设计[J]. 现代雷达,2015(4):73-76,80.

[4] 邓若汉,余金金,王洪彬,等. 基于Labview的ADC综合性能测试系统[J]. 科学技术与工程,2012,12(19):4653-4658.

[5] IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters[S]. IEEE Std. 1241-2000.

[6] IEEE Standard for Digitizing Waveform Recorders[S]. IEEE Std. 1057.2007.

[7] 张智慧,荆学东,丁虎. 噪声对高速ADC的动态性能影响分析[J]. 船舶工程,2015,37(3):58-63.

[8] Attivissimo F,Di Nisio A,Giaquinto N. Measuring Dynamic Nonlinearity of Digitizers Affected by Time Base Distortion[J]. IEEE Transactions on Instrumentation and Measurement,2011,60(2):560-566.

[9] Janik J,Fresnaud V. A Spectral Approach to Estimate the INL of A/D Converter[J]. Computer Standards and Interfaces,January 2007,29(1):31-37.

[10] Filippo Attivissimo,Nicola Giaquinto,Izzet Kale. INL Reconstruction of A/D Converters via Parametric Spectral Estimation[J]. IEEE Transactions on Instrumentation and Measurement,2004,53(4):940-946.

[11] Wagdy M F,Awad S S. Determining ADC Effective Number of Bits via Histogram Testing[J]. IEEE Transactions on Instrumentation and Measurement,1991,40(4):770-772.

[12] Ting H W,Liu B D,Chang S J. Histogram Based Testing Strategy for ADC[J]. Proceedings of the Asian Test Symposium,2006:51-54.

[13] Duan Jingbo,Chen Degang. SNR Measurement Based on Linearity Test for ADC BIST[J]. IEEE International Symposium on Circuits & Systems,2011,19(5):269-272.

[14] Duan Jingbo,Jin Le,Chen Degang. Testing ADC Spectral Performance without Dedicated Data Acquisition[J]. IEEE Trans Instrum Mear,2012,61(11):2941-2952.

AFastADCMeasurementApproachBasedonParameterExtraction*

CHENBao*,WANGFengzhou

(Department of Information and Electrical Engineering,XZIT,Xuzhou Jiangsu 221000,China)

As for traditional test method of ADC,it needs twice tests to obtain the static parameters and dynamic parameters. To obtain the whole parameters,it spends a long time,and the cost is very high. Firstly,the time of histogram algorithm is optimized by moving average filter. Then the test point of static test collection is extracted. After eliminating the errors of gain,all the dynamic parameters of ADC are obtained by fourier transform based on the parameter extraction algorithm. The experimental results show that the estimate errors of maximum INL,SINAD,ENOB,THD and SFDR are 0.168 LSB,0.211 dB,0.035,0.159 dB and 0.119 dB by using the optimized algorithm. Compared with the original algorithm,the estimating accuracy of SINAD and ENOB is increased by 0.411 dB and 0.057 dB. Compared with the traditional method,the test time is reduced by 50.769% on the promise of the test precision.

ADC test;test estimation;parameter extraction;moving average filter

10.3969/j.issn.1005-9490.2017.05.019

项目来源:住房和城乡建设部研究开发项目(2014-K5-033);江苏省高校自然科学研究项目(14KJB520038)

2016-08-08修改日期2016-09-29

TN98

1005-9490(2017)05-0045-06