结合频谱移位的二维傅里叶变换FPGA实现

2017-11-03钱辉,史瑶,龚敏,高博*

电子器件 2017年5期

关键词：傅里叶移位频谱

钱辉,史瑶,龚敏,高博*

(1.四川大学物理科学与技术学院微电子学系,成都 610064;2.微电子技术四川省重点实验室,成都 610064)

结合频谱移位的二维傅里叶变换FPGA实现

钱辉1,2,史瑶1,2,龚敏1,2,高博1,2*

(1.四川大学物理科学与技术学院微电子学系,成都 610064;2.微电子技术四川省重点实验室,成都 610064)

在三维成像技术中,对图像进行傅里叶变换之后需要通过频谱移位将零频集中到中心位置。为了提高图像处理的运算速度,提出了一种结合频谱移位的二维傅里叶变换的FPGA实现方法,将频谱移位结合到二维傅里叶变换硬件系统中,在实现图像二维傅里叶变换的同时也完成了一半的频谱移位。采用ALTERA 系列EP4CE115F29C7芯片,针对256×256的图像实现设计,最高工作频率分别达到84.2 MHz;资源消耗为3 849个LE。采用SignalTap Ⅱ Logic Analyzer工具实时验证了模块的正确性。

FPGA;二维傅里叶变换;频谱移位;图像处理

二维傅里叶变换和频谱移位是目前三维成像系统中非常重要的模块。二维傅里叶变换可以分解成两次一维傅里叶变换,先行变换再列变换[1-2]。二维傅里叶变换得到的图像频谱的零频是位于矩阵的4个顶角,为了方便进行频谱分析,需要进行频谱移位将零频移到矩阵的中心。频谱移位需要分别沿着行和列两个方向进行两次移位。傅里叶变换和频谱移位都需要进行两次变换,消耗大量的时间[3-5]。

本文基于Altera公司的FFT IP 核,提出了一种结合频谱移位的二维傅里叶变换的FPGA实现方法。通过改变二维傅里叶变换的列变换起始位置,从矩阵的中间列开始进行列变换,使得二维傅里叶变换频谱的零频从矩阵的4个顶角移到中间列,在完成二维傅里叶变换的同时完成了一半的频谱移位。

1 二维傅里叶变换和频谱移位的介绍

1.1 二维傅里叶变换

数字图像是一个时域上的二维函数,它包含了周期性成分、非周期性成分、噪声等信息,这些成分往往紧密交织在一起,很难进行分离和分析。傅里叶变换可以将图像时域的灰度分布函数变换为图像的频率分布函数,得到了不同频率的周期函数,可以更加方便地对这些频域信号进行处理、分析。

一维的离散傅里叶变换(DFT)可以用式(1)表示,逆傅里叶变换用式(2)表示,f(x)表示时域上的一维数字信号,x=0,1,…N-1[5-7]。

(1)

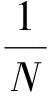
(2)

一维离散的傅里叶变换可以扩展到二维,用f(x,y)表示数字图像或大小为M×N的二维离散信号,u和v是离散的频域变量,x和y是离散的时域变量,M和N是二维矩阵的行数和列数。本文研究的是一个256像素×256像素大小的图片,所以令M=N=256。二维离散傅里叶变换对可以用式(3)、式(4)表示。

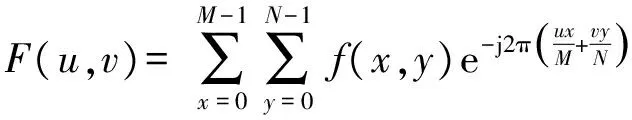
(3)

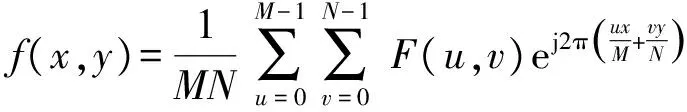
(4)

从式(3)可以看出二维的离散傅里叶变换可以分解成两次一维的傅里叶变换,先对f(x,y)进行一维的行傅里叶变换得到f(u,y),然后再对f(u,y)进行一维的列傅里叶变换得到F(u,v)。同时,每一次的变换都是只有一行数或者一列数独立地进行变换,所以无论从哪一列开始进行变换,都不会改变得到的频谱信息,只是改变了频谱的位置。

直接使用DFT的定义计算的计算复杂度为O(N2),即对N点的f(x)进行傅里叶变换需要进行N2次的复数乘法。实现一次复数乘法需要4次实数乘2次实数加,当N很大时,其计算量是相当可观,对于2-D图像处理,所需计算量更是大得惊人。本文实现的256×256像素大小的图像的二维傅里叶变换,则需要进行256×256×256×2=33 554 432次复数乘法。本文使用的FFTip是基于快速傅里叶变换算法实现的,快速傅里叶变换(FFT)是离散傅里叶变换的一种高效算法,可以将复杂度降低为O(N/2log2N),对于256×256大小的图像的二维傅里叶变换只需要进行262 144次复数乘法。随着处理图像的大小的增加,快速傅里叶变换的优势会更加明显。本文设计中使用的FFT IP核是高性能、高参数化的快速傅里叶变换(FFT)处理器[8-9]。

1.2 频谱移位

数字图像的二维傅里叶变换的频谱的零频分别位于矩阵的4个顶角,如图1(a)所示。为了更方便地对频谱信息进行处理和分析,需要通过频谱移位把零频集中到矩阵的中央,如图1(c)所示。

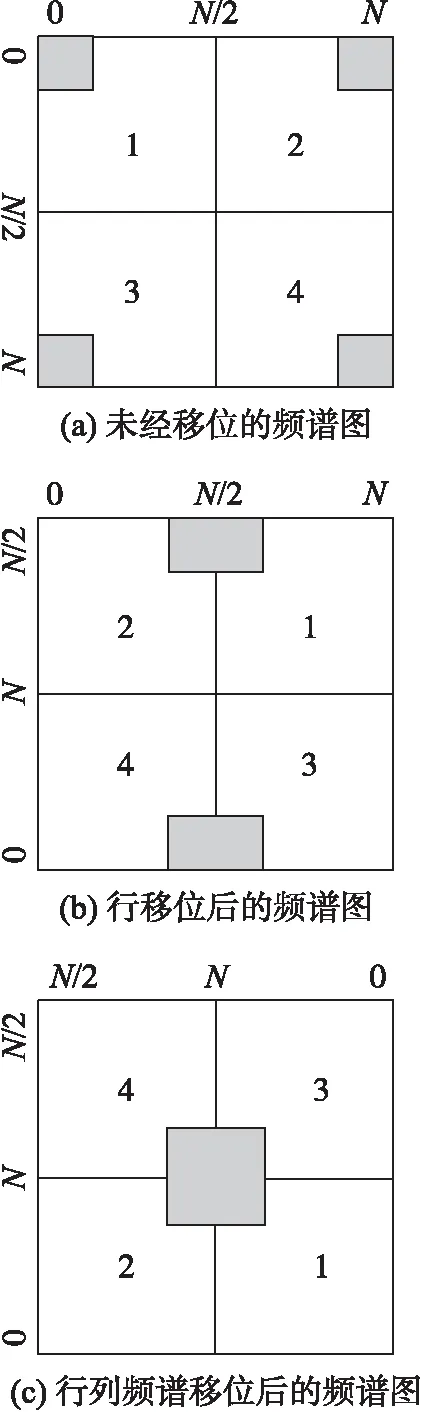
图1 二维图像频谱移位图

通常用软件对图像进行处理时是用MALTAB中的FFT2+fftshift()命令对原始图像进行二维傅里叶变换和频谱移位的[4-5]。如图1所示,把图像矩阵等分成4个小矩阵,频谱移位(fftshift)是实现矩阵1和4进行平移交换,矩阵2和3进行平移交换。在硬件上,频谱移位是通过对频谱信息的存储和地址变换来实现。首先对图1(a)的频谱的每一行进行移位,得到图1(b)的频谱图,然后对图1(b)的频谱图的每一列进行移位,最后得到图1(c)所示的频谱图,完成了频谱移位。频谱移位的硬件实现需要消耗大量的时间。

通过1.1节对二维傅里叶变换的分析可知,改变列变换的顺序不会改变频谱信息,所以考虑对图像的二维傅里叶变换的列变换进行改进,从第N/2列开始依次进行第(N/2)列至N列变换,然后从第0列开始依次进行第0列至(N/2-1)列变换。这样完成二维傅里叶变换之后得到的频谱如图1(b)所示,零频已经移到了矩阵的中间列。所以在二维傅里叶变换的完成的同时已经完成了一半的频谱移位,缩短了一半的频谱移位时间。

2 结合频谱移位的二维傅里叶变换的FPGA实现

二维傅里叶变换系统的FPGA实现框图如图2所示。clk是系统时钟,reset_n是系统的复位信号,start_ac为二维傅里叶变换的开始信号。主要的模块为FFT ip核模块、SRAM控制模块和RAM控制模块。

原始图片存储在SRAM中,像素信息按行为单元送入到FFT模块进行行变换,行变换的中间结果存入到RAM中,然后再从RAM中按列为单元读出数据送入FFT模块进行列变换,通过两次的一维傅里叶变换实现了二维傅里叶变换。

图2 二维傅里叶变换的硬件框图

2.1 FFT ip核模块

快速傅里叶变换在现代数字信号处理系统中是最常见的处理算法之一。Altera FFT IP核是高性能、高参数化的快速傅里叶变换(FFT)处理器,可以实现高性能的复数FFT或反FFT(IFFT)。FFT处理器的实现结构有缓存、突发、流和可变流结构。为了实现自然数顺序的输入和自然数顺序的输出,本文使用的是定点的可变流结构,数据变换长度为256,输入数据的精度为16 bit,旋转因子的精度为12 bit,输出数据的精度为25 bit[10]。旋转因子的精度越高,傅里叶变换的计算结果越精确。

FFT IP核接口信号如图3所示。左边部分信号是输入控制信号,右边部分是输出信号。

图3 FFT IP核接口信号

主要的接口信号的介绍:

Sink_real,Sink_imag:输入数据的实部和虚部;

Sink_valid:输入数据有效信号,当该信号为1时,FFT处理器认为输入的Sink_real和Sink_imag信号有效,所以可以通过控制该信号的值来控制FFT的运算的进行和暂停。

source_real,source_imag:输出数据的实部和虚部;

source_valid:输出数据有效信号,当该信号为1的同时就要控制RAM写数据。

2.1.1 行傅里叶变换

行傅里叶变换,可以看成是虚部为0的复数的傅里叶变换。在50 MHz的时钟频率下从SRAM中按顺序读出原始数据的实部(Sink_real),虚部(Sink_imag)直接赋值为0。行变换结果的实部和虚部分别存储在两个RAM中。

2.1.2 列傅里叶变换

从RAM按列的顺序从第129列开始依次读出第129列至255列的数据,再从读出第0列至128列的数据送入傅里叶变换模块进行列变换。

3 系统设计结果

系统针对256×256大小的图像完成二维傅里叶变换的过程,设计采用Verilog源代码以及 Altera公司的EP4CE115F29C7芯片进行原型验证,采用50 MHz为系统时钟,在Altera开发环境Quartus Ⅱ 13.0 SPI中综合,综合结果如表1所示。

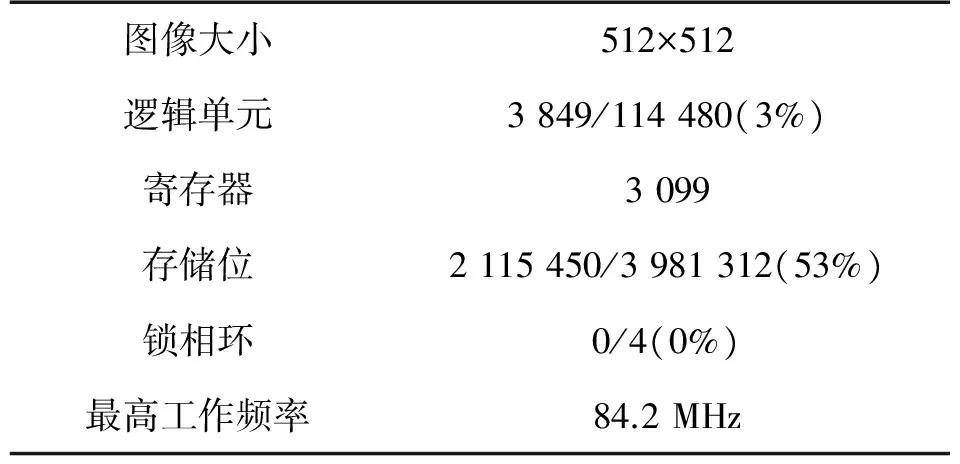
表1 综合分析报告

采用SignalTap Ⅱ logic Analyser 逻辑分析仪工具,以50 MHz时钟作为采样时钟,对该二维傅里叶变换模块进行了实时验证。图4是硬件验证的结果,图5是MATLAB软件仿真得到的结果,图6是两者的二维傅里叶变换的第129列的频谱的对比图,从图6可以看到两者的结果基本完全重合。误差在1%以内,误差存在的主要原因是MALTAB软件计算是用双精度浮点型数据类型进行计算的,而硬件实现是基于二进制计算的,所以精确度也会降低,这样的微小的误差不可消除,始终存在。

图4 FPGA实时验证得到的二维傅里叶变换结果(source_real_cut和source_imag_cut分别是得到的频谱的实部和虚部)

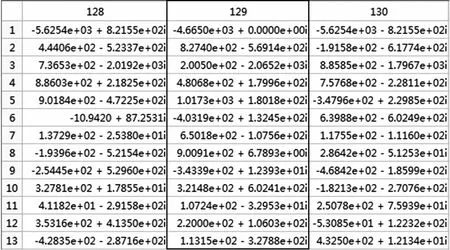
图5 MATLAB软件仿真得到的二维傅里叶变换结果(黑色方框中数据是得到的频谱的第129列的值)

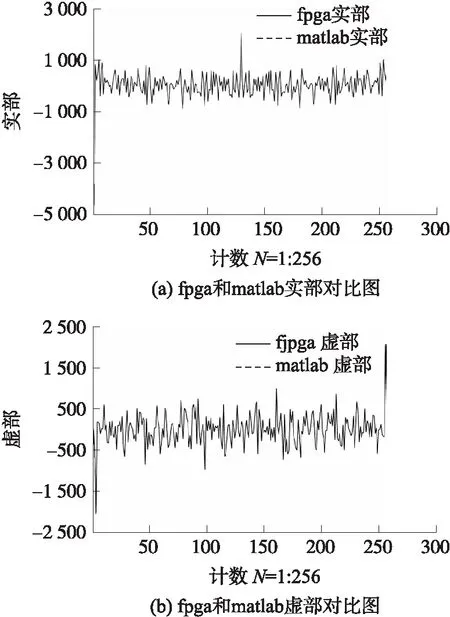
图6 FPGA和MATLAB计算结果对比图

硬件实现一开始得到的结果和软件仿真结果的第129列一致,说明该硬件系统实现了从图像的第129列开始进行列傅里叶变换,在完成二维傅里叶变换的同时把频谱的零频移到了矩阵的中间列。设计是通过改变列变换的起始列来实现频谱移位的,这种设计方法在完成一半的频谱移位的同时也不会给原来的系统增加额外的逻辑单元,不会影响原来系统的时序。

实现二维傅里叶变换和频谱移位均大约需要256×256×2=131 072个时钟周期的时间,本文设计的二维傅里叶变换系统可以节省一半的频谱移位的时间,节省二维傅里叶变换和频谱移位系统总耗时的25%。按50 MHz的频率计算,可以节省1.3 ms。实际的图像处理系统中,需要处理的图像的帧数非常多,图像的大小也可能会很大,如果处理的是大小为1 024×1 024的50帧的图像,就会节省大约1 s的时间,是非常可观的。

5 总结

本文结合频谱移位完成了256×256像素大小的图像的二维傅里叶变换的FPGA实现,并实时验证了该系统的正确性,最高工作频率达84.2 MHz。通过改变傅里叶变换的起始列,从行傅里叶变换的第129列开始进行列傅里叶变换,把频谱移位结合到二维傅里叶变换中,使得在完成二维傅里叶变换的同时也完成了一半的频谱移位,缩短了一半的频谱移位的时间,大大缩短图像处理系统的运算时间,为图像处理的硬件实现技术中频谱分析和处理提供了一种新的方法的思路。

[1] 杨军,于艳艳,陈成.基于FPGA的二维FFT处理器的研究与设计[J]. 云南大学学报(自然科学版),2013,35(06):750-755.

[2] Hojin Kee,Shuvra S. Bhattacharyya,Newton Petersen and Jacob KornerupR esource-Efficient Acceleration of 2-Dimensional Fast Fourier Tran-Form Computation on FPGAs[C]//Third ACM/IEEE International Conferenceon Distributed Smart Cameras.Como:IEEE,2009:1-8.

[3] 孙文昌,李忠科,杨威. 图像的傅里叶变换频谱特性分析[J]. 计算机与信息技术,2005(6):46-48.

[4] Abdellah M,Saleh S,Eldeib A,et al. High Performance Multi-Dimensional(2D/3D)FFT-Shift Implementation on Graphics Processing Units(GPUs)[C]//2012 Cairo International on Biomedical Engineering Conference. Giza:IEEE,2012:171-174.

[5] Zavadil J,Tuma J,Valicek J,et al. Two Dimensional Fourier Transform Using MATLAB[C]//2013 14th on International Carpathian Control Conference,Rytro:IEEE,2013:432-435.

[6] 刘微,朱明,李向荣,等. 运动模糊图像实时恢复的多DSP方案[J]. 电子器件,2005,28(4):722-725.

[7] 胡广书. 数字信号处理:理论、算法与实现[M]. 北京:清华大学出版社,2012:166-184.

[8] Anitha T G,Ramachandran S. Novel Algorithms for 2-D FFT and Its Inverse for Image Compression[C]//2013 International Conference on Signal Processing Image Processing and Pattern Recognit-Ion. Coimbatore:IEEE,2013:62-65.

[9] Vinay Kumar M,David Selvakumar A,Sobha P M. Area and Frequency Optimized 1024 Point Radix-2 FFT Processor on FPGA[C]//2015 International Conference on Vlsi Systems,Archit-Ecture,Technology and Applications. Bangalore:IEEE. 2015:1-6.

[10] 刘东华. Altera系列FPGA芯片IP核详解[M]. 北京:电子工业出版社,2014:172-286.

ImplementationofTwo-DimensionalFourierTransformCombinedwithSpectrum-ShiftingBasedonFPGA

QIANHui1,2,SHIYao1,2,GONGMin1,2,GAOBo1,2*

(1.Micro-Electronics of College of Physical Science and Technology,Chengdu 610064,China;2.Key Laboratory of Micro-Electronics Technology of Sichuan Province,Chengdu 610064,China)

In 3d imaging technology,after the Fourier transform of the image zero frequency will need to be concentrated to the center position by spectrum-shift. In order to improve the speed of image processing,a method of the implementation of two-dimensional Fourier transform combining with spectrum-shift is proposed based on FPGA. Combing the spectrum-shift with the two-dimensional Fourier transform hardware systems,the two-dimensional Fourier transform of the image and the half of the spectrum-shift can be achieved at the same time. The Altera chip of EP4CE115F29C7 was used in this design and the hardware implementation was completed for 256×256 of the image. The highest working frequency reached to 84.2 MHz. The amount of the resource usage reached to 3 849 LEs. The SignalTap Ⅱ Logic Analyzer has verified the correctness of the module realtimely.

FPGA;two-dimensional Fourier transform;spectrum-shift;image processing

10.3969/j.issn.1005-9490.2017.05.009

2016-08-19修改日期2016-10-23

TN402

1005-9490(2017)05-1092-05