股票型结构化信托产品平仓规则创新与下偏风险规避

马 磊(上海交通大学 安泰经济与管理学院，上海 200030)

股票型结构化信托产品平仓规则创新与下偏风险规避

马 磊
(上海交通大学 安泰经济与管理学院，上海 200030)

利用GARCH模型和蒙特卡洛模拟法，以沪深300为标的模拟在周度和月度平仓规则附加“即时”平仓规则下，股票型结构化信托产品的运行情况。结果表明：这种附加“即时”平仓条款的平仓规则创新能够在控制下偏风险的情况下提高合约的整体收益率和降低平仓的概率，因此建议在股票投资信托产品的合约设计中可以添加该条款，从而使得合约的运行更加平稳。

股票型结构化信托产品；GARCH模型；平仓规则创新；下偏风险规避

1 引言

股票型结构化信托产品作为证券投资信托产品中的“大头”，一直在中国的信托产品市场中扮演比较重要的角色。最近几年，该类信托产品更是经历了快速发展，2015年第二季度证券投资信托业务余额迈入3万亿元大关。到2015年末，证券投资信托业务余额为3.30万亿元，同比增长84.21%。证券投资信托业务规模占比从2011年的9.85%上升到2014年的14.18%。2015年末，股票型信托产品余额在11 103.74亿元左右，同比增长101.39%。证券投资信托产品业务快速发展带动股票型结构化信托市场规模快速扩张，但是这种结构化的信托产品在发展过程中也暴露了一些问题，主要包括：第一，运行的隐蔽性，其披露机制相对于基金产品完善度不够，特别是伞形信托产品，由于其隐蔽性市场很难监管；第二，各参数设定没有统一的标准和量化的指导性规则，譬如杠杆比率、平仓线等，因此市场比较混乱。

由于信托运行的隐蔽性，目前市场上对信托的参数设定及创新方面的研究较少，相关性较高的研究文献及主要的研究内容包括陈健宓(2012)[1]运用CPPI准则从提高结构化信托产品流动性、规范劣后级受益人参与资格、在信托合同中载明投资策略三方面提出了可行性建议；吴凌翔(2012)[2]以证券投资结构化信托产品的创新为切入点，引入“优先级夹层”方法，分析该金融创新方法如何影响证券投资信托产品的定价。其他针对平仓线设定和平仓风险评估的相关文章包括李宏伟、唐清泉、史庆盛(2008)[3]通过研究沪深300股指期货提出应对股指期货强行平仓风险的一种投资策略：当价格波动比较剧烈的时候,考虑强行平仓风险的投资策略与不考虑时的收益比会逐渐增大,也就是说,考虑到强行平仓风险的投资策略的优越性会越来越明显；王永杰、陈成、苏振华(2011)[4]采用建立在复合Poisson过程基础上的随机游走模型研究了目前市场上期货合约的风险，得出为了保证在有限的资金规模下投资的稳健性，减少每日结清带来的风险，必须严格控制投资规模的结论。

因此，从目前来看对于股票型结构化信托产品的研究还很不透彻，研究的切入点也较少。本文主要从股票型结构化信托产品平仓规则入手，考虑对目前市场上普遍存在的日度平仓规则进行创新，目的在于提高信托产品的收益、降低平仓概率，使信托产品的运行更加平稳。本文采用基于GARCH模型的蒙特卡洛模拟方法，分别研究在周度和月度平仓规则下标的信托产品的运行情况，同时文章考虑添加“即时”平仓条款来减少由于规则创新而引起的下偏风险的上升。

2 理论简介

2.1GARCH模型及相关理论

GARCH模型是一个专门针对金融数据量体定做的回归模型，除去和普通回归模型的相同之处，GARCH对误差的方差进行了进一步的建模，特别适用于波动性的分析和预测，这样的分析对投资者的决策能起到非常重要的指导作用，其意义很多时候超过了对数值本身的分析和预测。其具体形式如下：

(1)

(2)

(3)

ri：合约的当期收益率

ri-t：合约的第i-t期收益率

εi：残差项

N(0,1)：标准正态分布

hi：条件方差项

2.2VaR和CVaR相关理论

VaR的基本含义是风险资产在给定置信区间和持有期间上，在正常市场条件下的最大期望损失。

Prob(ΔP>VaR)=1-α

(4)

(5)

ΔP：一定持有期内的损失

α：置信水平

F：分布函数

CVaR是指投资组合的损失大于某个给定值的条件下,该组合损失的平均值，具体公式如下：

CVaR(α)= -E(r|r≤VaR)=

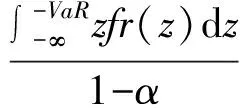
(6)

相关参数含义同上。

3 标的资产选取及参数估计

本文选取沪深300作为股票型结构化信托的投资标的，主要原因在于沪深300作为整个股票市场的规范性、指导性指标，从长期来看其运行情况可以近似代表市场的整体运行情况，采用此为研究标的得出的结果对整个市场的股票投资型信托产品的指导意义更强。

本文选取沪深300运行的时间段为2014—2017年2月，其收益率的相关描述性统计如图1，表1所示。

图1 收益率序列

均值方差最小值最大值中位数0．0005180．000315-0．0915400．0649890．000803

可以看出沪深300具有非常明显的波动率丛聚现象，而GARCH模型描述波动率尤其是在描述收益率的波动率丛聚方面较为有效，因此选用GARCH模型作为主模型是比较合理的。应用Eviews软件，发现GARCH(1,1)模型的拟合效果最好，得到模型的参数估计结果如表2所示。

表2 模型的参数估计结果

4 蒙特卡洛模拟与平仓规则创新

4.1平仓规则创新的主要思路

从平仓规则上讲，目前市场上各种产品大都采用日度平仓规则，像各种期权产品、融资融券等，证券投资信托产品也不例外，日度平仓规则占主流。但是，这种平仓规则存在一定的问题，尤其在市场表现较好时，因为当市场表现较好时，就算触及了平仓线，如果合约继续运行的话，那么在未来的时间段内标的资产价格运行超过平仓线价格的可能性依然很高。

本文平仓规则创新的初衷就是为了提高合约整体收益率的同时降低合约平仓的概率，因此本文设想周度和月度平仓这样两种情况，也就是在既定的平仓线下到周末和月末来确定合约是否平仓，而在中间如果合约触及平仓线而不去平仓，给予跌破平仓线的资产以“喘息”的机会，从而提高合约的收益和降低平仓概率。

4.2模拟运行结果及平仓规则修正

4.2.1模拟运行结果分析 本文的模拟过程采用R软件，模拟沪深300标的结构化信托合约在运行周期为200天的情况下，得出其平仓的次数、收益的均值、收益的方差等相关数据(由于复杂性，本文不考虑劣后级投资者在平仓情况下追加投资的情形)。本文模拟次数为10万次，在比较5%，10%，20%三个分位点的情况下，发现三者前后两次模拟的结果差的绝对值不超过万分之一，加之考虑本文数据在采用百分制的情况下保留三位小数的特点，该模拟结果可以用于后续的数据分析。

具体的模拟结果如表3所示。

表3选取在80%，70%，60%平仓线情况下，日度、周度、月度平仓规则下该合约的运行情况，选取80%，70%，60%三种平仓线的目的在于比较平仓线水平高低对平仓规则创新的影响。

通过以上分析可以得出以下结论：采用周度和月度平仓规则确实具有有效性，并且就目前的市场状况来看，给予平仓的调整空间越大，平仓发生的概率越低、标的资产的收益率越高。同时，在平仓线越高时进行平仓规则的创新所取得的收益率上升和平仓率下降的效果越明显。

表3 不同平仓线下日度、周度、月度相关模拟结果

4.2.2平仓规则创新过程中存在的问题探讨 从上面的分析过程中发现，虽然从整体来看收益上升了并且平仓的概率也下降了，但是合约整体的方差也随之上升，可以把这种情况看作收益上升所必须付出的一种代价。引起方差上升的根源来源于我们规则的创新，这种规则的创新引起方差上升的主要因素为虽然规则创新给予了触及平仓线的合约“喘息”的机会，合约的标的资产价格在之后的运行过程中会再次超过平仓线的价格，但是也会有一些合约在给予“喘息”机会之后，价格在规定期限内依然不能超过平仓线价格，更有可能价格会再次大概率下行。同时，一些当时躲过平仓命运的合约在后期仍然面临着被平仓的可能。这就是从整体来看方差增加的原因，我们认为其风险上升的主要原因来源于下偏风险的大幅上升。

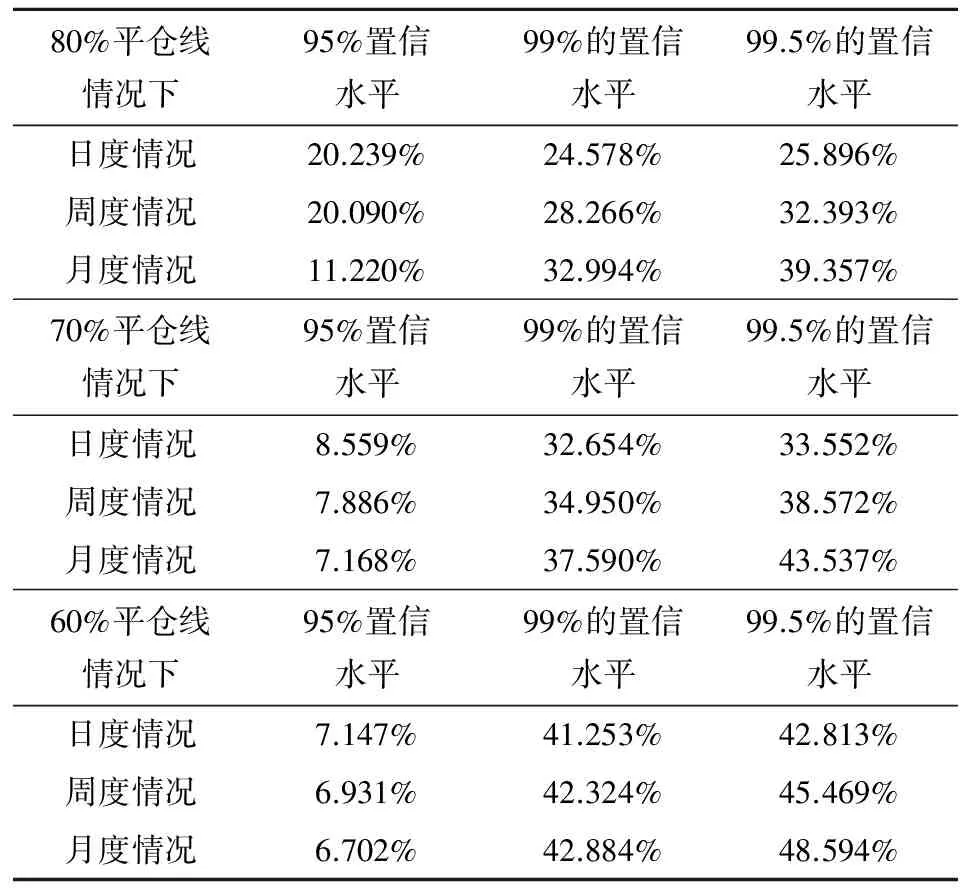
表4 不同平仓线、平仓规则和置信水平下合约运行周期内的VaR值

因此，本文选取VaR和CVaR作为观察指标，考虑在置信度水平为95%，99%和99.5%三种情况下，由于规则创新所带来的下偏风险的变化。

表4为各平仓线情况下， 95%，99%，99.5%的置信水平下，日度、周度和月度的最大损失率。从表4能够得到以下的分析结果：在控制下偏风险方面，当置信度水平相对较低时，周度、月度平仓规则能够取得比较好的效果。以80%平仓水平为例，在95%的概率下，日度平仓规则的最大损失率不大于20.24%；周度平仓规则的最大损失率不大于20.09%；月度平仓规则的最大损失率不大于11.21%，由此我们认为周度、月度平仓规则在低置信水平下起到了比日度平仓更好的控制下偏风险的效果。但是，当提高置信度水平时，周度和月度平仓规则下损失率却明显上升，下偏风险高于同一置信水平下的日度平仓规则，并且月度平仓规则损失率上升最快，这种现象符合之前的假设：月度平仓给予触及平仓线的股票价格更多的下降空间，因此在高置信水平下其损失率会明显上升。

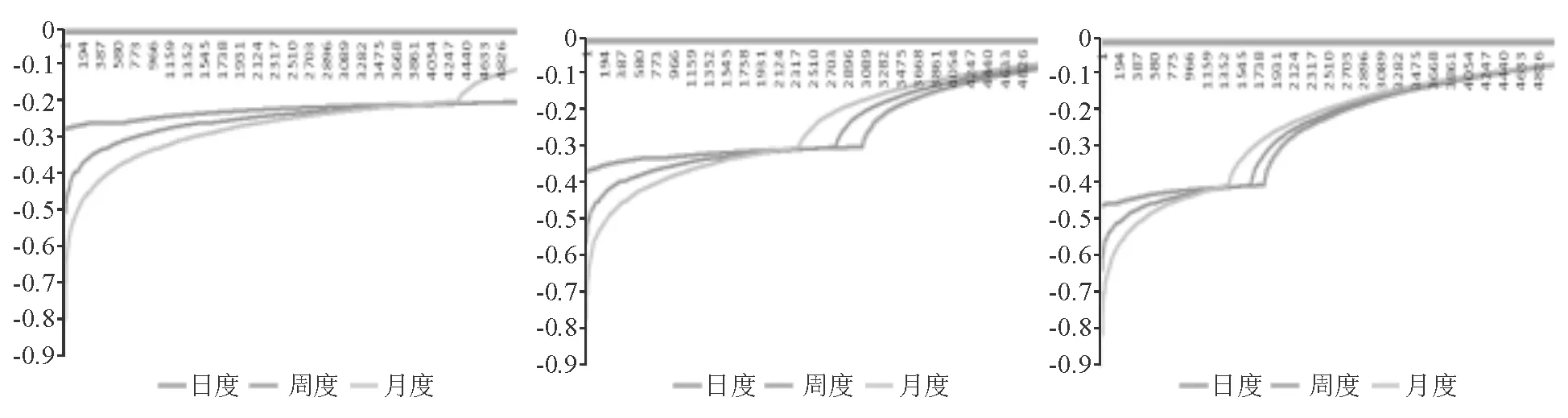
图2 80%，70%，60%平仓线情况下收益率最差的5 000次模拟情况的收益率分布情况

图2中三幅图分别为80%，70%，60%平仓线下，日度、周度、月度平仓规则下，收益率最差的5 000种模拟情况下的收益率折线图。从图2可以看出收益率在平仓线附近有个明显的跳跃，收益率在平仓线附近是分段的。同时，图2能够更加明显看出，当收益率以平仓线为界从右到左时，月度平仓规则相较周度和日度平仓规则的收益率越往左侧下降速度越快、下偏风险增加越多，这就更进一步证明了之前的结论。

表5为不同置信度水平下的CVaR值，从表5我们可以得出和VaR分析相似的结论：平仓规则的创新大大增加了下偏风险，尤其是在高置信水平和月度平仓规则下下偏风险暴露更加明显。

表5 不同平仓线、平仓规则和置信水平下合约运行周期内的CVaR值

总结以上分析结果可以得出：第一，采用周度和月度平仓规则确实可以降低平仓发生概率、提高整体收益水平；第二，由于周度、月度平仓规则给予了触及平仓线的合约以“喘息”的机会，因此整体来看其在下偏风险控制方面明显差于日度平仓规则，这可以看作提高收益而必须承担的风险。

4.2.3对平仓规则创新的修正 鉴于以上的分析结果，我们认为：就目前市场来看，应采用周度和月度平仓规则，从整体来看这种平仓规则可以提高合约的收益率、降低平仓的概率，使合约运行更加平稳。但是，采用这种规则整体来看却会加大下偏风险，虽然下偏事件真实发生的概率比较低，但是一旦发生却会造成较大的损失，对于风险厌恶者来说最好的情况是，希望能够完全消除这部分下偏风险，或者将其控制在一个可以接受的范围。

因此，本文考虑这样一种情况：如果在周度平仓和月度平仓的基础上添加一个条款，那么会不会在尽可能小地降低收益率的情况下消除大量的下偏风险，我们称之为对平仓规则创新的一种修正。

修正的主要出发点是考虑减少下偏风险，本文采用的一种可行的修正思路为在付出一定收益率为代价的情况下，我们锁定下偏风险的最大值，只要在锁定下偏风险这种情况下我们整体的收益率还是增加的同时整体平仓概率还是下降的，那这种情形下平仓规则创新还是能够优化之前的日度平仓规则。同时，相对于之前平仓规则理论上的完全下偏风险暴露而言，这种平仓规则可以完全锁定下偏风险。

4.2.4“即时”平仓条款 因此，本文考虑添加这样一个条款：以80%平仓线为例，采用周度平仓规则的情况下，当合约触及平仓线时，不平仓而是给予该合约一定的下跌空间，但是当合约继续下跌如跌破70%时，那么不管是否到了周度平仓时点，都强制其第二天开盘马上平仓。添加这样一个条款，除了市场出现极端流动性紧缩的情况，就可以完全规避合约跌破70%平仓线的风险，也许这样做减少了一部分收益率，但是却将下偏风险掌握在了可控范围，本文称这样一种条款为“即时”平仓条款。

下面本文同样应用上面的模拟运行数据结果来研究这种条款设计的合理性和有效性。

a) 周度、80%平仓线

b) 月度、80%平仓线

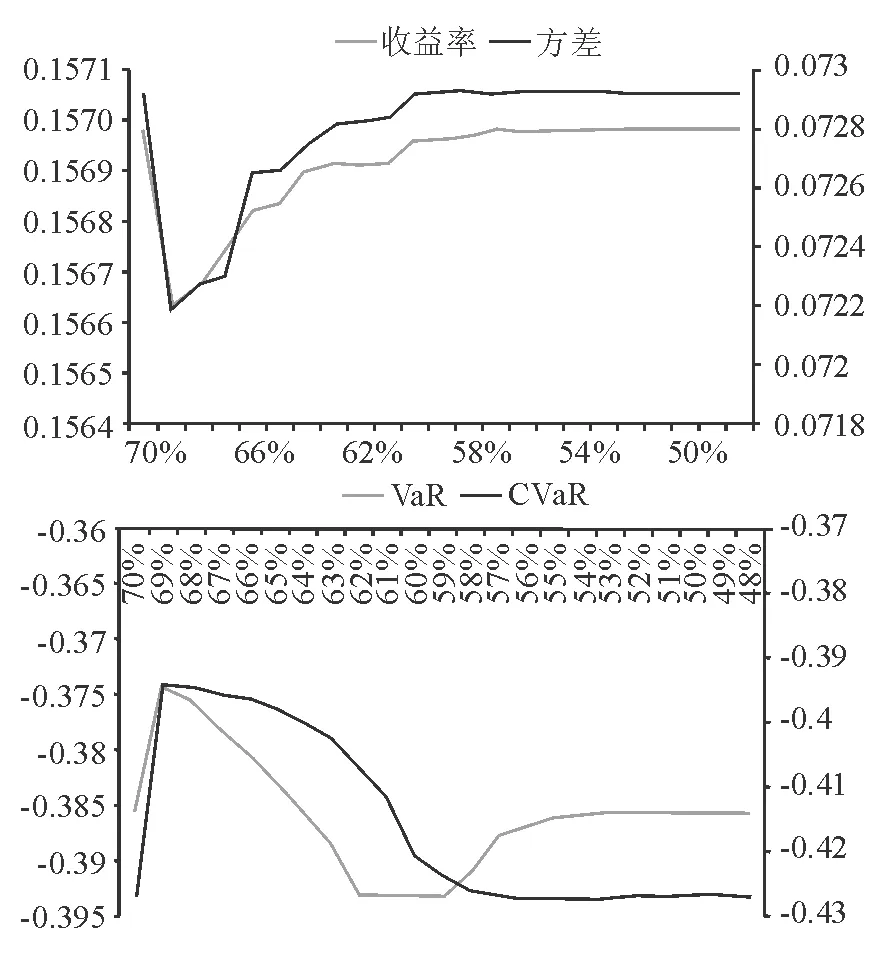
c) 周度、70%平仓线

d) 月度、70%平仓线

e) 周度、60%平仓线

f) 月度、60%平仓线

图3中六幅图分别为80%，70%，60%平仓情况下的收益率、方差和99.5%(主要考虑高置信水平的目的根据上文分析结果：在高置信水平情况下周度、月度平仓情况相对于日度平仓情况VaR和CVaR上升最多，也就是高置信水平下下偏风险上升最多，研究如何降低高置信水平下的下偏风险更具有意义)的置信水平下VaR，CVaR曲线。以a) 为例，a) 上图表示不添加即时平仓条款80%平仓线情况下，和添加即时平仓条款即时平仓线从79%～53%情况下收益率(左)和方差(右)；a) 下图横轴含义同上图相同，分别表示在这些即时平仓线情况下的VaR(左)和CVaR(右)值。

从图3可以看出，在设定即时平仓线的情况下，收益率和方差都会出现从原周度、月度平仓线瞬间下降的情形，而后随着即时平仓线的上升，收益率和方差会逐渐抬升，当即时平仓线越来越低时，收益和方差逐渐趋于平缓。VaR和CVaR也存在瞬间下降的情形，但是随着即时平仓线的下降，VaR和CVaR的运行规律有所不同，VaR逐渐增加超过原周度、月度平仓线到达最大值点后会重新下降，并逐步最终趋于原周度、月度平仓VaR值，而CVaR则是在跳跃之后缓步上升趋于原VaR和CVaR值。

同时，我们发现不管哪个即时平仓线状况下的收益率都高于原来的日度平仓情况下的收益，因此这种即时平仓规则的设定对提升合约的整体收益依然是有效的。

那么，在多种“即时”平仓线情况下，究竟应该选择哪一种作为最优即时平仓线，这主要取决于评价方法，本文认为以下两种方法具有可行性：

方法一：基于整体收益和方差的夏普比率方法

该方法考虑选用夏普比率作为选择即时平仓点的依据，假设无风险收益率为4%，比较不同即时平仓线下的夏普比的值，最大值点就是即时平仓点。以80%平仓线情况下各即时平仓线的周度平仓为例，其各即时平仓线情况下的夏普比如图4所示。

图4 80%平仓线周度情况下各即时平仓线下的夏普比

在该情况下，夏普比率最大化点 “即时”平仓线为77%时，就是该平仓规则下的最优“即时”平仓点。应用夏普比率可以找到任意平仓线水平下的最优“即时”平仓点。但是，这种方法考虑的是合约的整体风险，并没有考虑下偏风险的影响，因此可以考虑另外的方法。

方法二：更加注重下偏风险的方法：综合考虑VaR和CVaR

以80%平仓线周度平仓规则为例，当“即时”平仓线从大到小时，本文设置并考察两个指标：A=即时平仓线下收益率变化百分比/即时平仓线下VaR变化百分比，B=即时平仓线下收益率变化百分比/即时平仓线下CVaR变化百分比。设计这两个指标的合理性在于(以A为例)当即时平仓线下收益率变化百分比为负、即时平仓线下VaR变化百分比同时为负时，A的最小化代表以最小的收益代价换取了最大的下偏风险规避。

如果能够找到某一点，这点上A，B都为正且最小化，那么就可以认为在该周度、月度平仓情况下找到了最优即时平仓点，但是根据上面的图形分析，VaR和CVaR最小值点往往不会出现在同一个即时平仓点。

以80%平仓线、周度平仓规则下的99.5%的置信水平为例来研究如何找出最优即时平仓点，在1%的即时平仓线梯度下，得到表6所示结果。在表6结果中将该表分为四部分，分别表示为部分1，2，3和4。

本文将表6分为四部分的原因是：第一部分，指标A和指标B都趋于下降；第二部分，指标A在触底之后开始上升；第三部分，VaR值开始增加；第四部分，B值开始为负，且“即时”平仓线太低，风险控制能力较弱。以上四部分可以首先将第一部分排除，因为在该部分任意的即时平仓水平下其指标A和指标B都高于第二部分76%即时平仓线水平下的A，B指标。然后，应该排除第三部分，因为第三部分虽然指标B仍趋于下降但是VaR却上升了，这与降低风险的初衷相违背。对于第四部分而言VaR同样上升，另外排除第四部分的原因还包括第四部分的即时平仓线过低，其在风险控制方面放开的幅度过大，一旦市场整体收益下滑，那么其控制风险的能力将会非常有限。综合考虑，本文认为最优的即时平仓点应该处于第二部分，究竟第二部分哪一点才是最优点，取决于个人的风险厌恶函数。

表6 80%平仓线、周度情况下各“即时”平仓线下的相关指标统计表

更一般的情况下，可以建立A和B的函数，当然函数的具体形式取决于个人对于风险及对A，B的厌恶程度，在函数取正的最小值的情况下可得出最优化的“即时”平仓点。

5 结论和建议

本文重点研究股票型结构化信托产品的平仓规则创新，采用GARCH模型和蒙特卡洛模拟法，以沪深300为标的，结果表明：采用周度和月度平仓规则能够有效提高合约的整体收益率和降低平仓的概率，使合约运行更加平稳；同时，针对采用周度和月度平仓规则增加合约下偏风险的情况，文章考虑引入“即时”平仓条款，该条款的引入能够以最小的收益为代价完全控制合约的下偏风险，避免合约在极端情况下大幅下跌。根据本文的模拟运算结果，就目前的市场状况而言，该平仓规则创新具有比较明显的实用价值。

[ 1 ] 陈健宓. 结构化证券投资信托产品设计研究[D].上海交通大学，2012.

[ 2 ] 吴凌翔. 证券投资型结构化信托创新研究——以一个全能型创新信托产品为例[D].上海交通大学，2012.

[ 3 ] 李宏伟，唐清泉，史庆盛. 股指期货强行平仓风险应对策略的探讨[J].中山大学研究生学刊(自然科学、医学版)， 2008，29(3)：73-80.

[ 4 ] 王永杰，陈成，苏振华. 股指期货市场强行平仓风险估计[J].重庆工商大学学报(自然科学版)，2011，28(3)：261-264.

[ 5 ] [美]兹维·博迪和罗伯特·C.莫顿金融学[M].北京:中国人民大学出版社，2000.

[ 6 ] 陈松男. 结构式金融产品之设计与创新(一)[M].台北：新陆书局，2010：30-45.

[ 7 ] BLACK F, JONES R. Simplifying portfolio insurance [J].The Journal of Portfolio Management，1987(13): 48-51.

[ 8 ] BOROVKOV K A．DICKSON D C M．On the ruin time distribution for Sparre Andersen process with exponential claim sizes[J]．Insurance: Mathematics & Economics，2008(42): 1104-1108.

[ 9 ] ESTEP T, KRITZMAN M. TIPP: insurance without complexity [J].Journal of Portfolio Management, 1988,14(4):38-42.

[10] PEROLD A, SHARPE W. Dynamic strategies for asset allocation[J]. Financial Analyst Journal, 1988,51(1): 16-27.

[11] ROSS S M．Stochastic Processes[M].New York: John Wiley & Sons，INC，1996.

InnovationofClosingRulesforStockStructuredTrustProductsandtheFollowingRiskAversion

MALei
(Under Graduate Student of Antai College of Economics & Management, Shanghai Jiao Tong University, ShangHai 200030, China)

This article uses the GARCH model and monte carlo simulation method to research that how the hushen300 underlying trust product operates under the weekly and monthly closing rules with the addition of “immediate” closing lines. The result shows that the closing rules innovation added with the “immediate” closing lines can increase the whole yield rate and reduce the probability of the closing of the trust product, also, it can control the downside risk. As a result the article suggest to add the innovative term to the stock investment structured trust products, consequently the product will run more smoothly.

stock investment structured product; GARCH model; innovation of closing rules; avoid of the downside partial risks

F 064.1

A

2017-03-06

马磊(1989—)，男，江苏南通人，研究方向：金融工程。E-mail: 651197729@qq.com.

1005-9679(2017)05-0013-07