基于遗传非负矩阵分解的任务自动分配研究

毛 鹏， 章鸣雷， 胡传杉(浙江工业大学 经贸管理学院，浙江 杭州 310023)

基于遗传非负矩阵分解的任务自动分配研究

毛 鹏， 章鸣雷， 胡传杉
(浙江工业大学 经贸管理学院，浙江 杭州 310023)

随着众包模式的大量应用，众包平台上的任务出现了爆炸性增长，导致用户很难在大量的任务中找到适合自己的任务。近年来，国内外研究人员提出利用矩阵分解等算法来进行任务自动分配，其中非负矩阵分解由于可解释性好，能够缓解冷启动问题，准确度较高等优点受到了广泛关注。然而，非负矩阵分解算法的目标函数通常是不可微不连续的，且梯度搜索方法容易陷入局部最优。基于此，提出一种基于遗传算法的非负矩阵分解算法来实现众包平台任务的自动分配，利用遗传算法的全局最优性来提高算法的准确度。实验结果表明本算法在低维空间比经典的PMF算法，随机初始化的NMF算法和TaskRec算法具有更好的准确度。

遗传算法；非负矩阵分解；众包；任务分配

1 引言

众包由杰夫·豪[1]在2006年首次提出，它指机构把由员工执行的工作任务，以自由自愿的形式交给非特定大众网络的方法。随着众包模式的流行，众包平台任务呈爆发式增长，用户的任务选择越来越多，但是大量的任务信息也会使用户迷失在信息的海洋，需要用更多的时间和精力来寻找适合的任务[2]。如果众包平台有合适的任务分配算法，把合适的任务自动分配给合适的用户，那么将极大提高企业和用户的工作效率[3-5]。

Panagiotis等[6]对亚马逊的AMT众包平台进行了全面具体的分析，指出众包平台急需任务自动分配功能。Ambati 等[7]提出了基于分类技术的任务自动分配算法，但这种算法准确度不高且任务分类对算法准确度影响较大。Yuen等[5]在Ambati 的基础上加入了用户的任务选择历史数据，提出了TaskRank算法，然而TaskRank也需要对任务进行分类，而有些任务可能同时属于多种任务类型从而降低了算法准确度，这种算法也不能对新任务进行自动分配。Yuen等[8-9]之后提出了用PMF算法进行众包平台的任务自动分配，但是由于分解后的矩阵元素存在负值从而可解释差且算法准确度不高。Mejdl Safran等人[10]提出了众包平台的实时任务分配算法，证明了算法的计算效率，但是并没有说明算法任务分配的准确性。

基于这样的现实，本文提出遗传非负矩阵分解算法进行任务自动分配，根据用户历史任务完成情况，用户搜索信息等信息通过VBA编程建立用户-任务评分矩阵A，将其分解为用户潜在特征矩阵W和任务潜在特征矩阵H，通过两个矩阵乘积WH来预测矩阵A中对应元素的缺失值，给定一连串的任务，我们通过预测分数的高低给任务排序，将预测评分靠前的任务推荐给用户。

2 模型描述

(1)

令 ：

E=A-WH，eij是矩阵E的第i行第j列元素，那么E的F2范数可以表示为：

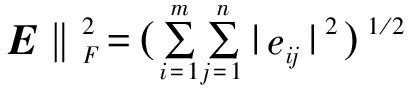
(2)

(3)

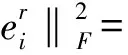
(4)

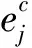
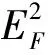
(5)

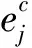
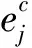
(6)

这里的式(1)是本文算法迭代阶段的评价函数，式(4)和(6)是算法初始化阶段的评价函数。

3 用户-任务评分矩阵的构建

本文从数据集中筛选出任务ID、用户ID和用户对任务的完成状态三列，按照表1的规则将用户不同的任务完成状态转换为不同的非负数值，然后进行VBA编程。首先，通过字典获得Hit ID和Worker ID的所有清单；其次，把获得的清单复制到矩阵结果表中；之后，通过字典获取相同Hit ID和Worker ID的分值的最大值；最后，通过字典的遍历来填充矩阵，从而建立用户-任务评分矩阵。图1阐明了用户-任务矩阵的建立过程。

表1 用户-任务评分矩阵的建立规则

图1 用户-任务评分矩阵的建立过程

4 传统的非负矩阵分解算法

传统的NMF算法使用梯度下降的方法进行用户-任务评分矩阵的分解，随机初始化一个用户潜在特征矩阵W和一个任务潜在特征矩阵H，然后按照式(7)(8)的乘性迭代公式交替优化它们。

(7)

(8)

但是，这样往往会导致算法陷入局部最小[12]，影响算法的准确度。

5 基于遗传算法的非负矩阵分解算法

本文算法随机初始化T个矩阵种群，然后在限定的搜索空间进行T个W和T个H的迭代优化，相对一个W和一个H而言，搜索空间更广，提高了算法的全局搜索能力。

令T代表种群个数，Pm表示矩阵的变异概率，Pc表示矩阵的交叉概率，s%表示矩阵W和H变异时矩阵元素发生变异的比例，k为分解矩阵的维度，迭代代数用gen表示，r为gen的最大值。

建立用户-任务评分矩阵后，本文提出的基于遗传算法的非负矩阵分解算法分为两个部分：矩阵初始化和矩阵的迭代优化。在矩阵分解的初始阶段，用PMX交叉和单点变异，以式(4)、(6)为评价函数进行两个非负矩阵的迭代优化直到指定的迭代次数，得到两个初始化的非负子矩阵。在此基础上，使用式(1)作为适应度评价函数，以矩阵随机行或列的交叉、矩阵固定比例元素的变异进行初始化后两个非负矩阵的迭代优化直到指定的迭代次数，此时得到的两个非负矩阵的乘积为原矩阵的近似矩阵。

5.1矩阵初始化阶段

由式(3)和(5)可知，矩阵E任何一个行向量或者列向量的F2范数变小都会使矩阵E的F2范数变小，因此在初始化阶段，最小化矩阵W每个行向量的F2范数使得式(4)值达到最小，在此基础上最小化矩阵H的每个列向量的F2范数使得式(6)的值最小。

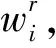
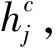
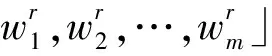
5.2矩阵迭代阶段

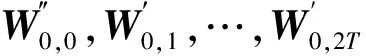
5)选择：若原数据以h%参与训练，那么B1,B2，…，B2T同样以h%相对应的元素、以公式(1)为评价函数进行B1,B2，…，B2T的选择，选择出使得评价函数最小的前T个B1,B2，…，B2T，也就是找到了最优的T个矩阵W和相应的T个最优的矩阵H；

6)回到第一步，继续以同样的遗传操作进行矩阵的迭代优化，直到gen=r；

7)得到分解后的非负矩阵W和H；

至此，整个算法的初始化阶段和迭代阶段执行完毕，将用户-任务评分矩阵A分解得到一个非负的用户潜在特征矩阵W和一个非负的任务潜在特征矩阵H。表2以伪代码的形式说明了算法的计算过程。

表2 基于遗传算法的NMF算法框架

6 遗传非负矩阵分解算法在众包平台任务自动分配的应用

为了方便解释，假设目标矩阵A是500*500的矩阵，随机选取80%的矩阵元素作为训练集，那么剩下的20%的元素就作为测试集测试算法的准确度。详细步骤有以下几步:

1)按照表1的规则，根据用户不同的任务完成状态将其转换为0～5对应的数值，在此基础上利用VBA编程将数值化后的数据集转换为矩阵的形式得到矩阵A；

2)随机抽取矩阵A80%的元素作为训练集，其余20%元素作为测试集。

3)将矩阵A需要预测的20%的元素取值为0，得到矩阵B；

4)将B用本文提出的算法分解为用户潜在特征矩阵W和任务潜在特征矩阵H，用W和H的乘积来近似原矩阵A；

5)将矩阵A未参与运算的元素，即20%的测试集与矩阵W，H乘积WH相应的元素进行比较；

通过以上6个步骤，就完成了众包任务自动分配过程。

7 算法仿真实验

本文首先建立用户-任务评分矩阵，然后通过基于遗传算法的非负矩阵分解算法来预测矩阵的缺失值，给定一连串的任务，通过预测分数的高低给任务排序，将预测评分高的任务优先分配给用户。本章将在Matlab的实验环境下验证算法的任务分配准确度。

7.1实验参数设置

W和H的上下边界限定在[0,max(A)]，变异概率取值为0.1，变异时矩阵元素发生随机变异的比例为1%。交叉概率取值0.8，种群数量为100，迭代代数设置为500。文章代码采用Matlab语言编写，实验平台为Intel(R)Core(TM)M330,4.00GB RAM,实验环境为Matlab2012.a(7.14.0.739)。

7.2实验结果验证指标

本文采用均方根误差RMSE和平均绝对误差MAE两个指标来验证算法的任务自动分配准确度。对于测试集中的用户w和任务h，awh表示用户w对任务h的实际评分，Awh是遗传非负矩阵分解算法的预测评分，那么RMSE和MAE可定义为：

(9)

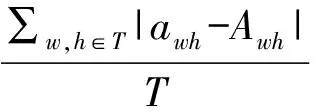
(10)

这两个指标是评价算法分配准确度最常用的评价指标，RMSE和MAE值越小，表示任务分配越准确。

7.3实验结果分析

本文的数据集与Man-Ching Yuen的数据集都取自NAACL 2010年公开的亚马逊众包平台AMT上的数据。每次实验的结果都是取10次实验指标的平均值。以RMSE和MAE两个指标与经典的PMF算法，随机初始化的NMF算法，Man-Ching Yuen等人的TaskRec算法作比较，实验结果如表3至表6所示。为了方便算法实验结果的描述，用大写字母GN来表示本文提出的基于遗传算法的非负矩阵分解算法。本文实验结果将从RMSE分析， MAE分析，GN算法与随机初始化的非负矩阵分解算法比较，变异算子分析，交叉算子分析五个方面进行详细的数值分析，验证本文提出的算法准确度和参数对算法准确度的影响。

7.3.1RMSE指标分析 本文在K=5和K=15的维度下验证GN算法的任务分配准确度。通过表3、表4的实验数据，可以发现，在维度K=5时，GN的RMSE指标优于PMF 和TaskRec，在K=15时GN算法RMSE指标好于TaskRec，部分好于PMF算法。具体来说，本文提出的GN算法RMSE角度的准确度比PMF算法平均提高了24.7%，比TaskRec算法平均提高了39.4%。

7.3.2MAE指标分析 通过表5、表6的实验数据，可以发现，在维度等于5时，GN的MAE指标好于PMF和TaskRec，在维度为15的时候，算法的准确性部分优于PMF，好于TaskRec。具体来说，本文提出的基于遗传算法的非负矩阵分解算法的MAE角度的准确度比PMF算法平均提高了37.7%，比TaskRec算法平均提高了46.6%。

7.3.3GN算法与随机初始化的NMF算法准确度比较分析 传统的矩阵分解算法在矩阵初始化阶段是随机初始化的，本文提出的GN算法使用遗传算法进行矩阵的初始化，由表3至表6可知，本文算法的RMSE角度的准确度比随机初始化的NMF算法平均提高了28.5%，MAE角度的准确度比随机初始化的NMF算法平均提高了35.6%。因此，使用遗传算法进行矩阵的初始化能够显著提高算法的准确度。

7.3.4变异算子分析 在维度K=5，Pc=0.8的情形下测试不同的变异概率对指标RMSE和MAE的影响。由图2、图3可知，当变异概率值Pm从0.05逐渐增大的时候，RMSE和MAE值不断下降，说明算法的推荐准确度不断提高，然而当变异概率Pm超过0.25并继续增大时，RMSE和MAE指标值也随之增大，说明推荐准确度逐渐下降。因此，最优的变异概率Pm大概是0.25左右。

7.3.5交叉算子分析 在维度K=5，Pm=0.1的情形下测试不同的交叉概率Pc对指标RMSE和MAE值的影响。由图4、图5可知，当交叉概率值Pc从0.3逐渐增大的时候，RMSE和MAE值不断下降，说明算法的推荐准确度不断提高，然而当交叉概率Pc超过0.5并继续增大时，RMSE和MAE指标值也随之增大，说明推荐准确度逐渐下降，最优的交叉概率Pc大概是0.5左右。

表3 80%和60%训练集不同维度下RMSE指标值

表4 40%和20%训练集不同维度下RMSE指标值

表5 80%和60%训练集不同维度下MAE指标值

表6 40%和20%训练集不同维度下MAE指标值

图2 变异概率Pm对RMSE的影响

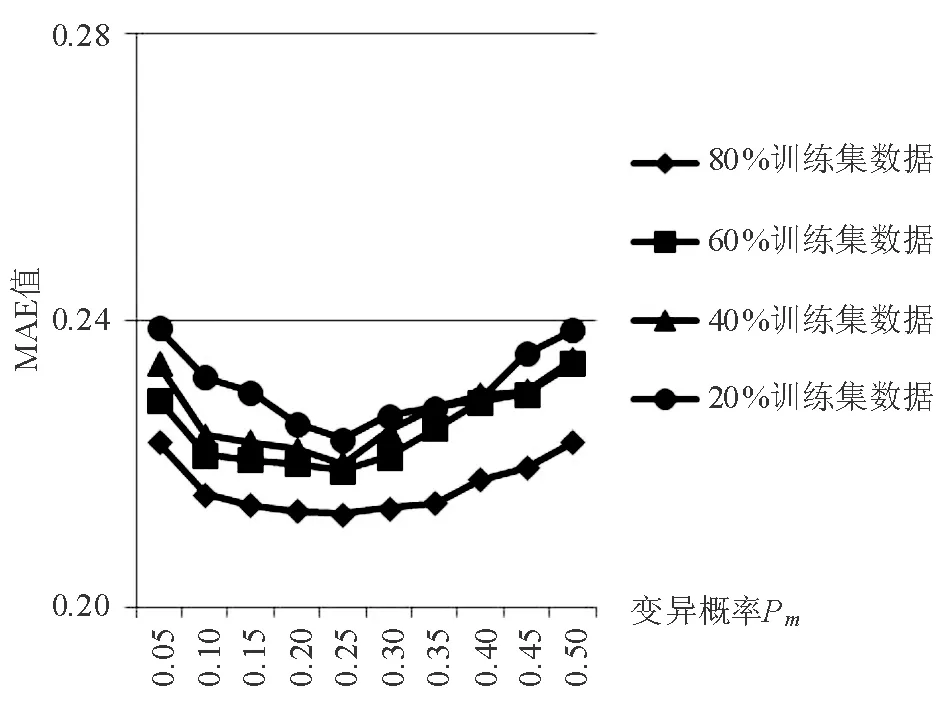
图3 变异概率Pm对MAE的影响

图4 交叉概率Pc对RMSE的影响

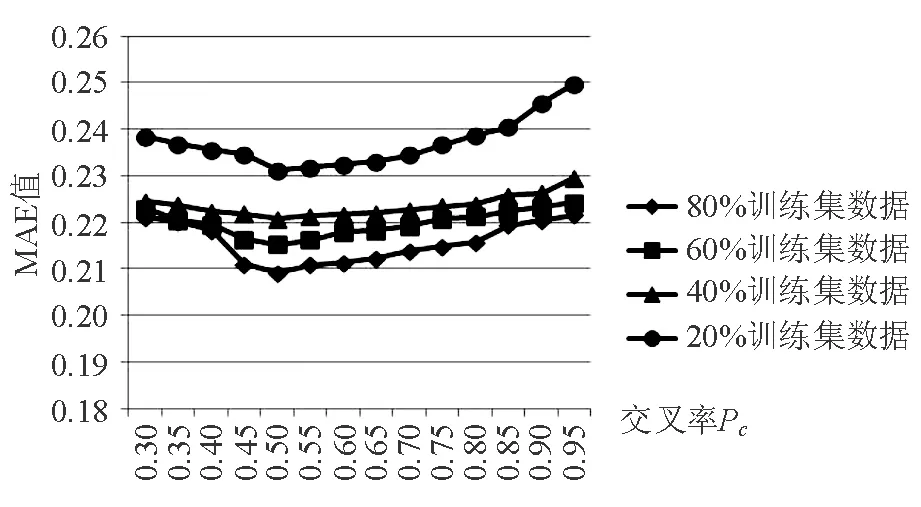
图5 交叉概率Pc对MAE的影响

8 结束语

本文针对众包平台任务自动分配问题提出了一种基于遗传算法的非负矩阵分解算法，利用遗传算法的全局最优性来提高算法的准确度。

通过实际数据的测试，发现本文提出的算法在低维空间具有较好的准确度。此外，由于本文算法直接在用户-任务评分矩阵上进行非负分解，因此分解后的非负子矩阵具有良好的解释性，避免了复杂的任务分类且缓解了冷启动问题。

目前，众包平台任务自动化分配还是一个较新的领域，未来可以从构建众包平台进行真实数据采集，采用高级推荐算法、大规模分布式计算等方法进行研究。

[ 1 ] HOWE J. The rise of crowdsourcing[J]. Wired Magazine, 2006, 14(6): 176-183.

[ 2 ] 侯文华，郝琳娜.众包模式-企业创新的新助力[M]. 北京：科学出版社，2016：1-101.

[ 3 ] STEFFEN S, SVENJA N, SEBASTIAN S. Perceived Task Similarities For Task Recommendation in Crowd-sourcing Systems[C]∥Proceedings of the 25th International Conference Companion on World Wide Web, 2016: 585-590.

[ 4 ] CHILTON L B, HORTON J J, MILLER R C. Task Search in a Human Computation Market[C]∥Proceedings of the ACM SIGKDD workshop on human computation, 2010: 1-9.

[ 5 ] YUEN M C, KING I, LEUNG K S. Task Matching in Crowd-sourcing[C]∥IEEE International Conferences on Internet of Things, and Cyber, Physical and Social Computing, 2011.

[ 6 ] PANAGIOTIS G. IPEIROTIS. Analyzing the Amazon mechanical turk market place[J]. XRDS: Crossroads, 2010, 17(2): 16-21.

[ 7 ] AMBATI V, VOGEL S, CARBONELL J. Towards task recommendation in micro-task markets[J]. Human computation, 2011(11): 11.

[ 8 ] YUEN M C, KING I, LEUNG K S. Task Recommendation in Crowdsourcing Systems[C]∥ACM, crowdkdd, 2012.

[ 9 ] YUEN M C, KING I, LEUNG K S. Taskrec: a task recommendation framework in crowd-sourcing systems[J]. Neural Processing Letters, 2015, 41(2): 223-238.

[10] MEJDL S, DUNREN, CHE. Real-time recommendation algorithms forcrowd-sourcing systems[J]. Applied Computing and Informatics, 2016: 124-133.

[11] 孟祥武，刘树栋，张玉洁.社会化推荐系统研究[J]. 软件学报，2015，26(6)：1356-1372.

[12] LEE D D, SEUNG H S. Algorithms for Non-negative Matrix Factorization[C]∥NIPS, 2001: 556-562.

ResearchonAutomaticAssignmentofTaskBasedonTheGeneticNMF

MAOPeng，ZHANGMinglei，HUChuanshan
(College of Economics and Management, Zhejiang University of Technology, Hangzhou 310023, China)

With the crowd-sourcing used widely, the task in crowd-sourcing platform has exploded, which makes it difficult for users to find appropriate tasks in a large number of tasks. In recent years, domestic and foreign researchers have proposed the use of matrix decomposition algorithm to carry out automatic assignment of tasks. Especially NMF has gained tons of attention because of its advantages, such as good explanation, accuracy and alleviating the cold start problem. However, the objective function of the NMF algorithm is usually non-differentiable and discontinuous, and the gradient search method is easy to fall into the local optimal. Based on this, this paper proposes a NMF algorithm based on genetic algorithm to realize the automatic allocation of the task in crowd-sourcing platform, and the global optimality of the genetic algorithm is used to improve the accuracy of the algorithm. The experimental results show that the proposed algorithm has better accuracy compared with the classical PMF algorithm, randomly initialized NMF and TaskRec algorithm in low dimensional space.

genetic algorithm; nonnegative matrix decomposition; crowd-sourcing; task assignment

TP 181

A

2017-04-13

毛鹏(1991—)，男，湖北咸宁人，硕士研究生，主要研究领域为遗传算法，推荐系统。E-mail：793944046@qq.com.

1005-9679(2017)05-0098-06