含时滞和非单调接触率手足口传染病模型的稳定性分析

官金兰，赖煜庭，陈芷棋

（广东农工商职业技术学院基础部，广东广州510507）

含时滞和非单调接触率手足口传染病模型的稳定性分析

官金兰，赖煜庭，陈芷棋

（广东农工商职业技术学院基础部，广东广州510507）

依据手足口病在实际中流行的特点，用依赖变量S的非单调的接触率函数来表示一系列的外部和内部因素的影响，并在手足口病动力学模型中引入双时滞，建立含时滞且具有非单调接触率的手足口病模型，再将模型转化为线性化线性系统。探讨了模型的无病平衡点和地方病平衡点的存在性及稳定性，得知模型有唯一的无病平衡点，并且在5种情况下，讨论了地方病平衡点的存在性。最后分析得知，无病平衡点在基本再生数大于1时是不稳定的，地方病平衡点是全局渐近稳定的。

手足口病；基本再生数；无病平衡点；地方病平衡点

已有的对手足口病模型的研究，接触率是单调的，甚至是饱和的。然而在现实生活中，许多疾病的传染率由于多种因素的影响，在单调递增后并不会趋于饱和。目前，对于手足口病患者都会采用发病后立即隔离的措施，以免疾病再次传播，这样接触率函数只和易感染者有关，而与患者无关。所以在本文中，依据手足口病在实际中流行的特点，用依赖变量S的非单调的接触率函数来表示一系列的外部和内部因素的影响，并在手足口病动力学模型中引入双时滞，建立含时滞且具有非单调接触率的手足口病模型，可以更好地研究疾病潜伏期和恢复者免疫期对传染病传播规律的影响，从而提出更加贴近实际的传染病防控策略。

1 建立模型

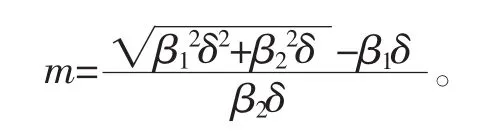
基于以上假设，文献［1］研究了以下具有非单调接触率的手足口病模型

其中S（t），I（t），R（t）分别为t时刻易感者、染病者与恢复者的人数，Λ为人口的外部输入（假设都是易感者），μ为自然死亡率，α为染病者的自然恢复率，而γ为指康复者个体丧失免疫力又回到易感者类的转化率，参数Λ，μ，α和γ都为正的常数，参数β2和δ为非负的常数。

为了更实际地描述手足口病的传染规律，考虑时滞对疾病的影响，研究下面含时滞且具有非单调接触率的手足口病模型

其中，N（t）为t时刻的总人口数，S，E，I，Q和R分别为易感者、潜伏者、染病者、住院隔离者和恢复者个体数目，Λ为常数输入率，β1为考虑促进因素和抑制因素前的常数接触率，β2为促进因素，δ为抑制因素，γ为染病者丧失免疫力转为易感者的转化率，μ为自然死亡率，d为因病死亡率，α为潜伏者转为染病者和住院隔离者的转化率，ρ为染病但不需要住院隔离的人占患者总数的比例，σ为住院隔离者的恢复率，w为疾病潜伏期，τ为恢复者对疾病的免疫期。

注意到系统（2）除第2个方程外，均不含E（t），因此本项目中，将系统（2）转为研究以下子系统

2 定性分析

2.1 平衡点的存在性

模型的无病平衡点即为系统（3）的常数解，显然，系统（3）有唯一的无病平衡点 E0=（N0，0，0）。根据文献［2］的方法，定义基本再生数为

为了求出系统（3）的地方病平衡点，令

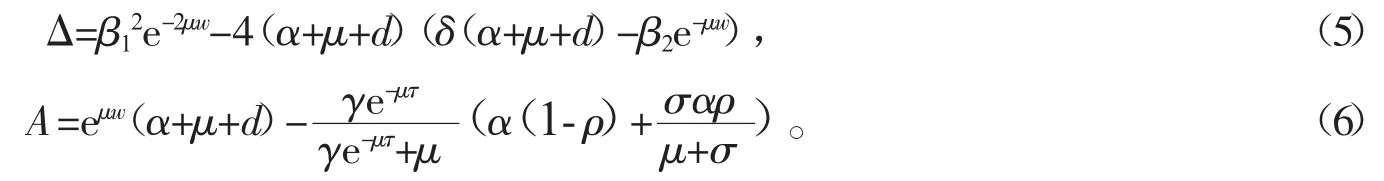
根据系统（3），经过计算可得

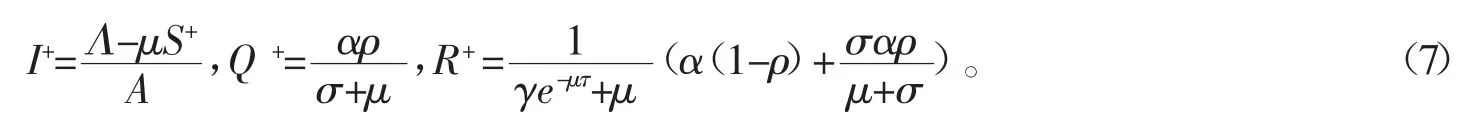
S+由如下方程决定

为了分析系统（3）的正解，即系统（3）的无病平衡点的存在性，下面对方程（8）进行讨论。

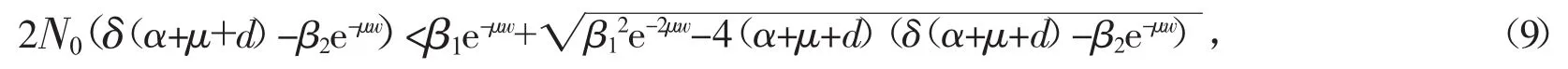
（3）β2e-μw＜δ（α+μ+d）。假设 Δ≥0，系统（3）可以很容易求到 2 个正解，即

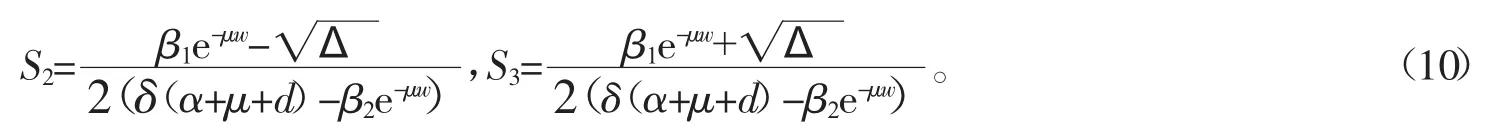
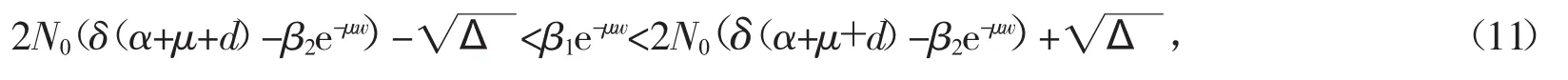
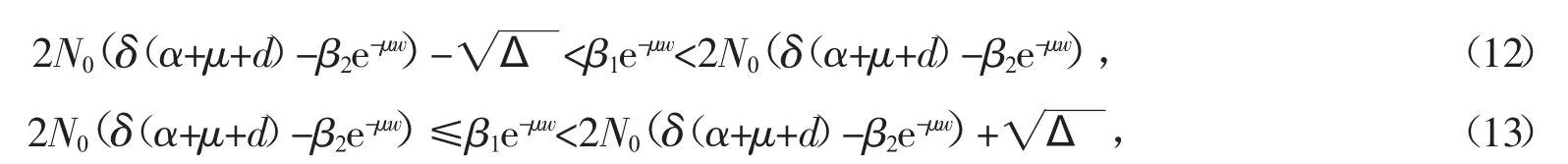
这蕴含有即 Si＜N0，现在分两种情形讨论 I2和 I3的存在性。

情形 1 Δ＞0

当 I2＞0 且 I3＜0 时，可以得到

式（12）和式（13）同时成立，先假设式（12）成立，可得

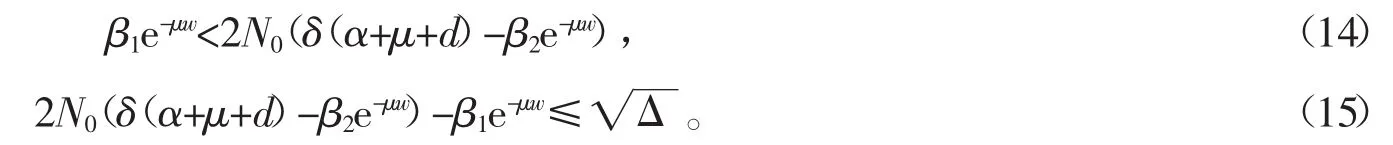
其中式（14）平方可以得到R0＞1。再假设式（13）成立，可以得到

用同样的方法可以得到其等价条件为

因此

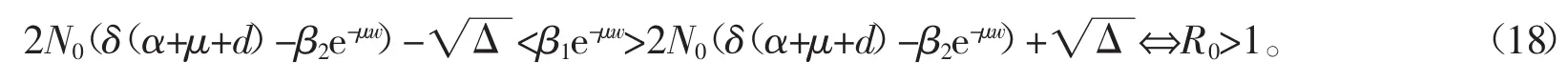
当I2＞0且I3＞0时，可得，类似以上讨论，可以得到以下结论

情形2 Δ＝0

当I2＝I3＞0时，依据Si＜N0，可得β1e-μw＜2N0（δ（α+μ+d）-β2e-μw），从而可得

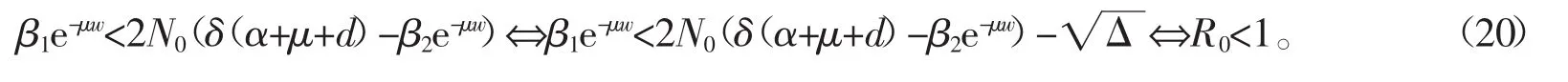
综合以上讨论，有以下结论：

（1）若 β2e-μw=δ（α+μ+d），当 R0＞1时，E1=（S1，I1，Q1，R1）是系统（3）的唯一地方病平衡点，当 R0≤1时，系统（3）没有地方病平衡点，此时

（2）若β2e-μw＞δ（α+μ+d），当 R0＞1时，E2=（S2，I2，Q2，R2）是系统（3）的唯一地方病平衡点，当 R0≤1 时，系统（3）没有地方病平衡点，此时

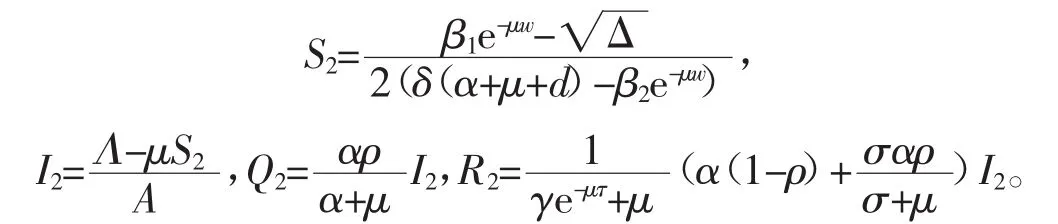
（3）若 β2e-μw＜δ（α+μ+d），当 R0＜1与 Δ＞0 同时成立时，系统（3）有 2 个地方病平衡点 E2=（S2，I2，Q2，R2）和 E3=（S3，I3，Q3，R3），此时

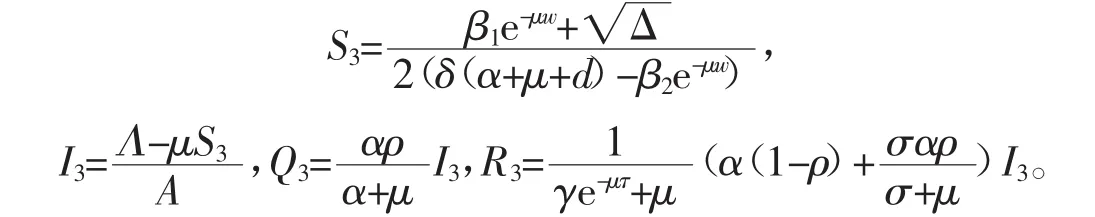
（4）若 β2e-μw＜δ（α+μ+d），当 R0＞1与Δ＞0同时成立时，E2=（S2，I2，Q2，R2）是系统（3）的唯一地方病平衡点。

（5）还有一种特殊情况就是，若 β2e-μw＜δ（α+μ+d），并且当 R0＜1与 Δ=0同时成立时，那么 E2，E3合并成系统（3）的一个二重根，即

2.2 平衡点的稳定性

2.2.1 无病平衡点的稳定性

（1）经过计算得知关于 S（t）的函数 H（S（t））在上单调递增，且为的最大值，分别讨论 R0＞1和 R0≤1且时，系统（21）的无病平衡点的稳定性。由文献［2-5］中的定理3.1可得到，系统（3）的无病平衡点E0在R≤1且同时成立时，在系统（3）的正向不变集中是局部稳定的。

（2）接下来讨论当R0＞1时无病平衡点的稳定性，为了方便研究系统（3），将其变为线性化系统：令x （t）=S （t）-，y （t）=I （t），z（t）=Q （t），u （t）=R （t），而相应的可行域为则系统（3）的线性化系统为

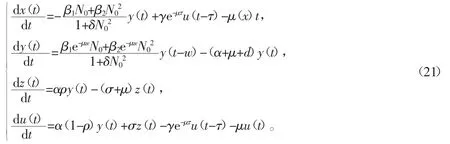
经过MATLAB计算，得到系统（21）的特征方程为

当R0＞1，即有f（0）＜0，并且当λ→+∞时，f（λ）→+∞。因此必定存在一个λ（λ＞0），使得f（λ）=0，即系统（21）必定存在一个正实部的特征根，所以无病平衡点在R0＞1时不稳定。

2.2.2 地方病平衡点的稳定性

为了书写方便，用E+=（S+，I+，Q+，R+）表示所有地方病平衡点Ei（i=1，2，3，*）。令x（t）=S（t）=S（t）-S+，y（t）=I（t）-I+，z（t）=Q（t）-Q+，u（t）=R（t）-R+，经过平移变换后，系统可化为如下系统

其中

系统（3）的地方病平衡点Ei=（i=1，2，3，*）的局部稳定性等价于系统（22）的零解的全局稳定性。根据文献［2-5］中的推论3.1可知，系统（22）的零解是全局渐近稳定的，即系统（3）的地方病平衡点局部渐近稳定。

3 结论

本文探讨了含时滞且具有非单调接触率的手足口病模型的无病平衡点和地方病平衡点的存在性及稳定性，得知模型有唯一的无病平衡点，并且在5种情况下，讨论了地方病平衡点E0=（N0，0，0，0）的存在性。最后分析得知，无病平衡点在基本再生数大于1时是不稳定的，地方病平衡点是全局渐近稳定的。本文所探讨的模型平衡点的存在性及稳定性仅仅是理论上的探讨，为了能使结论更具有说服力，还需要做的就是对模型进行数值模拟，从而对结论进行验证，这也是接下来需要解决的问题。

［1］李勇.中国手足口病动力学模型与数据模拟［D］.武汉:华中师范大学,2014.

［2］VAN DEN DRIESSCHE P,WATMOUGH J.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease teansmission［J］.Math Biosic,2002（180）:29-48.

［3］HALE J K,LUNEL S M V.Introduction to functional defferential equations［M］.NewYork:Springer-Verlag,1993.

［4］KUANGY.Delay differential equations with.applications in population dynarnics［M］.New York:Academic press,1993.

［5］HALE J K.Theory of functional differential equations［M］.NewYork:Springer-Verlag,1977.

Stability analysis of hand foot and mouth infectious disease model with time delay and non monotonic contact rate

GUAN Jin-lan,LAI Yu-ting,CHEN Zhi-qi
（Department of Basic Course,Guangdong AIB Polytechnic College,Guangzhou 510507,China）

Based on the epidemic characteristics of the hand-foot-mouth disease,using non monotonic contact rate of the dependent variable function K(S)to represent a series of external and internal factors,not in the hand,foot and mouth disease dynamics model introduced in double time delay,and thus establish a touch delay and have not monotonous content,foot and mouth disease model,and then linearized model can be converted to a linear system,discusses the model disease-free equilibrium and the existence and stability of the endemic equilibrium,told of the disease-free equilibrium model is the only,and in 5 cases,the existence of the endemic equilibrium is discussed.Finally,it is found that the disease-free equilibrium is unstable when the basic regeneration number is greater than 1,and the local disease equilibrium is asymptotically stable.

hand-foot-mouth disease;basic regeneration number;no disease equilibrium;local disease equilibrium

R311

A

1008-0171（2017）05-0049-05

2017-07-04

广东省大学生攀登计划培育项目（pdjh2017b0658）

官金兰（1982-），女，广东韶关人，广东农工商职业技术学院副教授，博士。

【责任编辑：王桂珍 foshanwgzh@163.com】