函数项级数一致收敛柯西判别法的改进形式
2017-11-02邢家省杨义川
邢家省,杨义川
(1.北京航空航天大学数学与系统科学学院,北京100191;2.数学、信息与行为教育部重点实验室, 北京100191)
函数项级数一致收敛柯西判别法的改进形式
邢家省1,2,杨义川1,2
(1.北京航空航天大学数学与系统科学学院,北京100191;2.数学、信息与行为教育部重点实验室, 北京100191)
考虑函数项级数和含参变量广义积分的一致收敛性的判别问题,经典的柯西准则判别法是证明函数项级数和含参变量广义积分一致收敛的有效方法,然而应用柯西准则判别函数项级数和含参变量广义积分非一致收敛时,对每一个问题都要给出各自具体细致的操作过程,相当的繁琐,没有形成系统的理论方法。经过对经典的柯西准则的表述方式给予改进,利用改进表述的柯西准则,给出了函数项级数和含参变量广义积分的非一致收敛性的一般性方法,叙述简便,通过实例说明改进的柯西准则的表述方法的技术指引性和对在具体问题使用中的简洁性,容易掌握并有利于传播。
函数项级数;含参变量广义积分;一致收敛性;柯西准则;非一致收敛
函数项级数和含参变量广义积分的一致收敛性的判别问题是数学分析中的重要内容,经典的柯西准则判别法是证明一致收敛的常用有效方法[1-8]。在经典文献[1-8]中,应用柯西准则判别非一致收敛时,是对每一问题给出一个表述过程,各不相同,表述过程和具体操作显得有点繁琐,没有形成一套理论方法。在综合文献[1-19]中的思想方法的基础上,发现可以对经典的柯西准则的表述方式给予改进,利用改进的柯西准则,给出了证明一些函数项级数和含参变量广义积分的非一致收敛性的一般性方法,通过大量实例证明改进的表述方法的技术指引和在具体使用中的简便性,以理论方法统一的形式传播,达到数学分析学中应有的理论高度。
1 函数项级数一致收敛柯西准则的改进形式
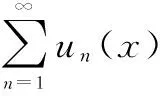
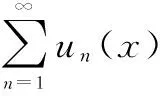
|SnN+pN(xN)-SnN(xN)|≥ε0。
定理2是证明函数项级数非一致收敛的常用方法,然而应用此方法时,需要每一个问题就要给出一个具体的叙述过程,表述非常的繁琐,没有体现出技术指引性。可以将定理1的结果的表述形式给予改进,改进后的形式方便于使用。
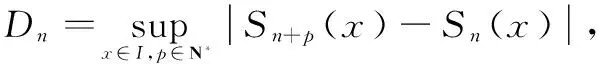
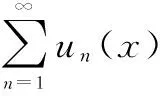
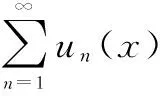
应用定理4,在证明函数项级数非一致收敛时,技术指导路线明确,具有一般性,表述简便。
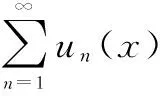
定理3的表述,来源于定理5的思想,定理3的表述方式达到统一完善的理论体系。
2 一些函数项级数非一致收敛的证明方法
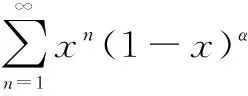
证明成立
pxn+p(1-x)α
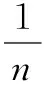
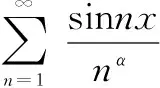
证明事实上成立
Dn≥|Sn+p(x)-Sn(x)|=

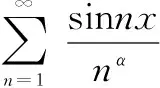
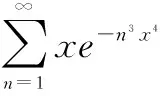
证明成立
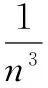
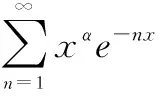
证明成立
3 含参变量广义积分一致收敛的柯西准则的改进
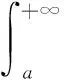
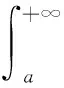
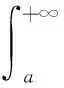
定理7是证明含参变量广义积分非一致收敛的常用方法,然而应用此方法在证明各个含参变量广义积分非一致收敛时都要重复的叙述一遍,表述有些繁琐。可以将定理5结果的表述形式给予改进,使其方向性明确,方便于使用。
记

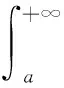
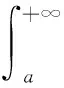
应用定理8,在证明含参变量广义积分非一致收敛时,技术指导路线明确,具有一般性,表述简便。
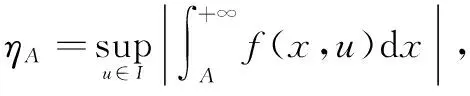
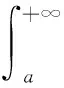
定理8的表述方式来源于定理10的思想,定理8的表述方式达到了与定理10统一完善的理论体系。
4 一些含参变量广义积分非一致收敛的证明方法

证明由不等式ey≥1+y,(y∈[0,+∞)),得
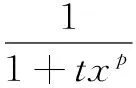
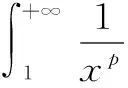
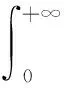
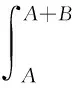
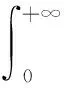
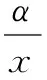
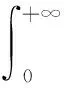
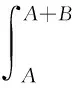
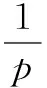


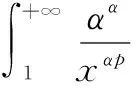
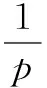
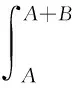
5 一个发散数列的例子
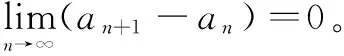
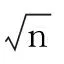
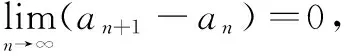
6 结束语
本文通过对函数项级数一致收敛的柯西准则的表述形式给予改进,找到了判别函数列非一致收敛的一般性方法,利用该方法,对各种问题的解决给出了技术指引方向,叙述统一简便,达到理论完善高度统一,并有利于掌握和传播。
[1] 黄玉民,李成章.数学分析(下册)[M].2版.北京:科学出版社,2007.
[2] 华罗庚,著.王元,校.高等数学引论(第二册)[M].北京:科学出版社,2009.
[3] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2002.
[4] 常庚哲,史济怀.数学分析教程(下册)[M].北京:高等教育出版社,2003.
[5] 陈纪修,於崇华,金路.数学分析(下册)[M].2版.北京:高等教育出版社,2003.
[6] 菲赫金哥尔茨.微积分学教程(第二卷)[M].8版.北京:高等教育出版社,2006.
[7] 卓里奇.数学分析(第二卷)[M].4版.北京:高等教育出版社,2006.
[8] 匡继昌.实分析与泛函分析(续论)(上册)[M].北京:高等教育出版社,2015.
[9] 白玉兰,陈述涛.一个二次广义积分的顺序交换问题[J].哈尔滨师范大学自然科学学报,1987,3(3):13-18.
[10] 匡继昌.Dirichlet积分九种解法的思路分析[J].高等数学研究,2012,15(4):61-64.
[11] 邢家省,杨小远,白璐.两无穷区间上积分交换次序充分条件的改进及其应用[J].四川理工学院学报:自然科学版,2016,29(1):87-92.
[12] 邢家省,杨小远.广义菲涅尔积分的积分交换次序计算方法[J].四川理工学院学报:自然科学版,2016,29(3):85-92.
[13] 邢家省,杨小远,白璐.菲涅尔积分计算中的一致收敛性的证明方法[J].吉首大学学报:自然科学版,2016,37(5):1-9.
[14] 邢家省,杨义川,王拥军.菲涅尔积分的几种计算方法[J].四川理工学院学报:自然科学版,2016,29(5):88-96.
[15] 邢家省,杨义川,王拥军.函数列的广义积分的极限定理及其应用[J].吉首大学学报:自然科学版,2016,37(6):1-9.
[16] 赵香兰.几种判别函数项级数非一致收敛的方法[J].大同职业技术学院学报,2003,17(4):50-62.
[17] 王庆东,王路桥.一种判定函数列非一致收敛的方法[J].高师理科学刊,2016,36(9):12-14.
[18] 王庆东.一种判定含参变量无穷限反常积分非一致收敛的方法[J].高师理科学刊,2016,36(1):15-19.
[19] 邢家省,杨义川,王拥军.函数列的黎曼积分的极限定理及其应用[J].四川理工学院学报:自然科学版,2017,30(3):73-78.
TheModifiedFormofSeriesofFunctionsviaCauchyCriterionofUniformlyConvergence
XINGJiasheng1,2,YANGYichuan1,2
(1.School of Mathematics, Beihang University, Beijing 100191,China;2.LMIB of the Ministry of Education, Beihang University, Beijing 100191,China)
Considering the discrimination of uniform convergence of the Series of functions and generalized integrals with parametric variables, Cauchy criterion discrimination is an effective method to prove series with function terms and improper integral with variable which is uniformly convergent, but for non-uniform convergence, Cauchy criterion is fairly cumbersome to apply. So a general method for the non-uniform convergence of the function term series is improved and the generalized integrals with parametric variables is given. This improvement is easier to apply and master through a large number of examples.
series of functions; generalized integral of parametric variable; uniformly convergence; Cauchy criterion; non-uniform convergence
O177.2
A
2017-07-20
国家自然科学基金项目(11271040);北京航空航天大学校级重大教改项目(201403)
邢家省(1964-),男,河南泌阳人,副教授,博士,主要从事偏微分方程、微分几何、泛函分析方面的研究,(E-mail)xjsh@buaa.edu.cn;
杨义川(1970-),男,甘肃天水人,教授,博士,主要从事逻辑代数、序代数、软计算及其应用方面的研究,(E-mail)ycyang@buaa.edu.cn
1673-1549(2017)05-0074-05
10.11863/j.suse.2017.05.13
