γ′-Fe4N的结构和热力学性质的第一性原理计算

袁玉全，丁雪枫，吴必达，张高杰，杨玲

(四川理工学院物理与电子工程学院，四川自贡643000)

γ′-Fe4N的结构和热力学性质的第一性原理计算

袁玉全，丁雪枫，吴必达，张高杰，杨玲

(四川理工学院物理与电子工程学院，四川自贡643000)

采用基于平面波模守恒赝势密度泛函理论的第一性原理方法研究了γ′-Fe4N的结构，获得了其零温零压下的晶格常数、常温下的体弹模量以及弹性常数等基本性质参数，其计算结果与其他理论计算结果和实验值符合较好。同时应用准谐德拜模型，成功获得γ′-Fe4N的相对体积、相对晶格常数、体弹模量、热膨胀系数以及热容随着温度、压强的变化关系。

密度泛函理论；准谐德拜模型；热力学性质

引言

铁及合金经氮化处理后形成的间隙合金相，可以大幅度地改善材料的性能，因此，对其机理的研究，引起了人们的极大兴趣。早在20世纪50年代就有人开始研究Fe-N化合物，当时的主要目的是想建立磁性与金属-非金属键之间的关系，1971年Kim和Takahashi发现Fe16N2的强磁性之后，研究工作由单纯的物理现象的研究发展到将Fe-N系列推向实际应用，研究的对象主要集中在Fe2N、Fe4N、Fe16N2等几种合金相[1-9]。

钙钛矿结构的γ′-Fe4N相具有面心立方结构，其中N原子占据面心立方结构的γ-Fe相的体心中心位置。虽然该化合物的饱和磁化强度略低于纯铁的饱和磁化强度，但γ′-Fe4N具有抗氧化，耐腐蚀及机械强度高等优点，具有比a″-Fe16N2相更高的热稳定性[10]。

自从Jack首先用x射线衍射研究确定了γ′-Fe4N晶体结构以来，人们相继用电子衍射、核磁共振、穆斯堡尔谱及高压等方法对它进行了系列研究[11]，但关于γ′-Fe4N在高温高压这样的条件下其结构以及热力学性质方面的研究还很少。本文利用第一性原理平面波赝势密度泛函理论[12-13]详细研究了γ′-Fe4N的基本性质参数，同时应用准谐德拜模型[14]对γ′-Fe4N的热力学性质进行系统地研究。

1 理论方法

1.1电子结构计算

对于电子结构计算，运用Materials Studio中的CASTEP程序，采用由Lin等为减少平面波截断能而提出的模守恒(norm-conserving)赝势方法[15]。计算中，Fe和N的价电子分别取3d64s2和2s22p3，选用了广义梯度近似(GGA)[16-17]交换相关函数PBE[18]。为保证计算精度，k空间Monkhorst-Pack格点[19-20]和平面波截断能分别设置为10×10×10和600 eV，当总能量之差小于10-6eV.atom-1时则认为自洽收敛。通过平面波赝势密度泛函理论实现对所有电子结构总能量的计算。

1.2热力学性质

使用准谐德拜模型研究钙钛矿结构的γ′-Fe4N相热力学性质。在准谐德拜模型中，γ′-Fe4N的非平衡Gibbs函数G*(V;P;T)定义为：

G*(V;P,T)=E(V)+PV+AVib(V;T)

(1)

其中：E(V)表示每个γ′-Fe4N原胞的总能量，P表示压强、V表示体积、T表示温度，AVib表示振动的Helmholtz自由能。由于使用了准谐近似和声子态密度的德拜模型，AVib可表示为[21-22]：

AVib(Θ;T)=

(2)

其中：Θ表示德拜温度，kB表示玻尔兹曼常数，n表示每个原胞中包含的原子数，D(Θ/T)表示德拜积分。对各向同性固体，Θ可表示为[21]：

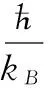
(3)

其中：M表示每个原胞中分子的质量，BS表示晶体压缩率的绝热体弹模量，BS可以表示为[14]：

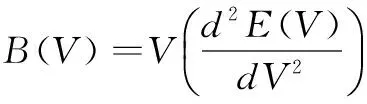
(4)

其中：f(σ)的表达形式可参阅文献[23-24]，泊松比率(Poisson ratio)σ取0.25[25]。再将非平衡Gibbs函数G*(V;P;T)对体积求最小值，即可得：

(5)

由此可得热状态方程。

热膨胀系数α、热容Cv、和等温弹性模量BT分别表示为：

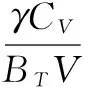
(6)

(7)

(8)

其中：γ是格林爱森(Grüneisen)参数。

2 结果与讨论

γ′-Fe4N具有钙钛矿的晶格结构，其中每个原胞内有4个Fe原子和1个N原子，其空间群为pm-3m(221)[26]。由几何优化后得到的晶格常数a=3.785 Å，因此在计算中晶格常数a的值取3.40 Å～4.00 Å的一系列值，对不同的晶格常数a，分别求出其相对应的总能量E、原胞体积V的值，然后将求出的能量和体积值采用Birch-Murnaghan Equation of State(EOS)状态方程进行数值方法拟合，其表达式为：

ΔE(V)=E-E0=

(9)

式中，E0表示零压下的静态能量，Vn=V/V0表示相对原胞体积，而压强与相对体积的关系为：

(10)

由此得到γ′-Fe4N的结构在零温零压下的平衡晶格常数a、常温下的体弹模量B0以及弹性常数，见表1。计算结果与其它理论计算结果[26-29]以及已有实验结果[30-31]符合较好。

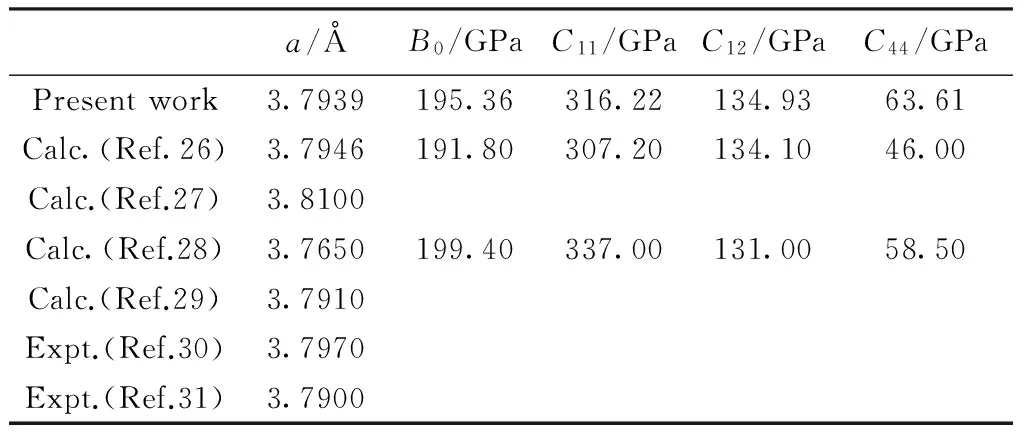
表1 零温零压下的晶格常数a、常温下的体弹模量B0和弹性常数Cij

通过对γ′-Fe4N在不同温度下体积随压强变化情况的计算，给出了相对体积V/V0(V0表示零压下给定温度的体积)、相对晶格常数a/a0(a0表示零压下静态晶格常数)随压强P的变化关系，如图1所示。在温度相同情况下，相对体积V/V0随着压强P的增加而减小；当压强一定情况下，高温区域的相对体积比低温区域的相对体积要小，这表示固体中的粒子在温度较高时其热运动会加快从而导致此固体更容易被压缩。通过内嵌图中当T=0K时的相对体积V/V0、相对晶格常数a/a0与压强P的关系，利用数值拟合就可以得到V/V0和a/a0关于压强的三阶多项式关系，当T=0K时：

V/V0=0.9974-0.00374P+2.15352×10-5P2

-5.74736×10-8P3

(11)

a/a0=0.99925-0.00128P+6.69456×10-6P2

-1.74589×10-8P3

(12)

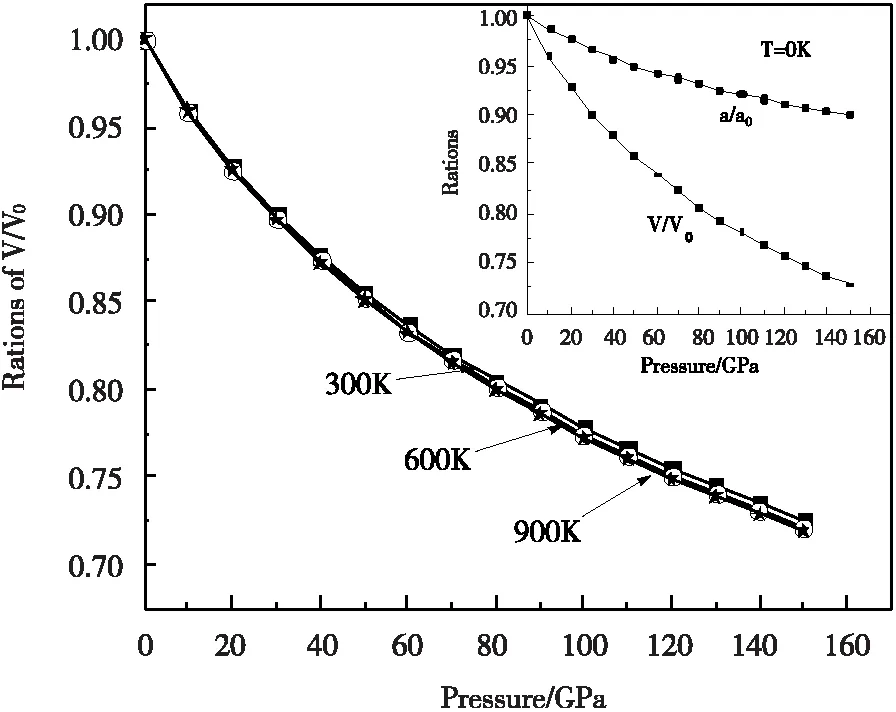
图1 相对体积V/V0与压强P的关系

图2是利用准谐德拜模型计算得到的零压下，体弹模量B随温度T的变化关系。从0 K～700 K过程中，当温度T<50 K，体弹模量B几乎保持不变；当温度T>50 K后，体弹模量B随温度T的增加而急剧减小。由此可知，当温度T<50 K时，晶格常数a几乎保持不变，这使得γ′-Fe4N的体积随温度变化很小；而一旦当温度T>50 K后，随着温度T的增加，晶格常数a快速增加，因此体积也跟着迅速增加，而由于结构体积的急剧增加就必然导致体弹模量B的快速减小。把体弹模量B和温度T拟合成一个四阶的多项式，得到：

B=226.01855+0.00576T-1.37456×10-4T2+

2.36701×10-7T3-1.1859×10-10T4

(13)

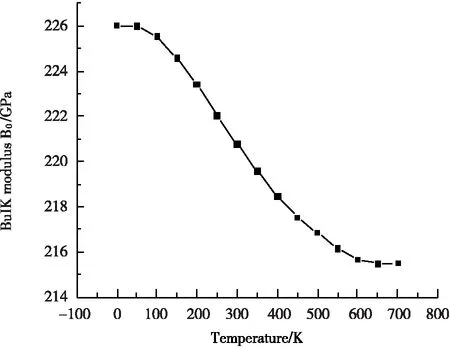
图2 零压下体弹模量B跟温度T的关系

图3给出了当温度T分别为0、300 K、600 K时，压强在0～150 GPa范围内体弹模量B变化情况。显然，同一温度下，随着压强P增加，体弹模量B相应增加；而相同压强下，随着温度T增加，体弹模量B相应降低。这主要是因为对材料增加压强和降低温度而产生的效应几乎是相同的。

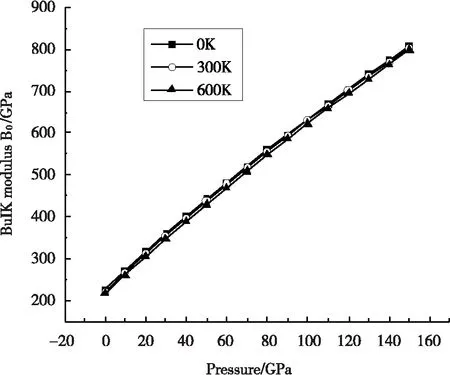
图3 不同温度下体弹模量B随压强的变化关系

图4为通过准谐德拜模型得到的γ′-Fe4N的热膨胀系数α随着压强和温度的变化情况。由图4可知，在零压下，当温度较低时，热膨胀系数α随温度的增加呈指数形式急剧增加；而当温度较高时，热膨胀系数α随温度的增加逐渐接近于线性增加趋势；随着压强P的增加，尤其在高温情况下，热膨胀系数α随着温度的变化趋势变得平缓。另一方面，在某一温度下，热膨胀系数α随着压强P的增加呈现出显著减小的趋势。特别值得注意的是，当温度T等于500 K和600 K时的热膨胀系数α非常接近，这意味着在高温高压下，温度和压强对γ′-Fe4N的热膨胀系数α影响较小。

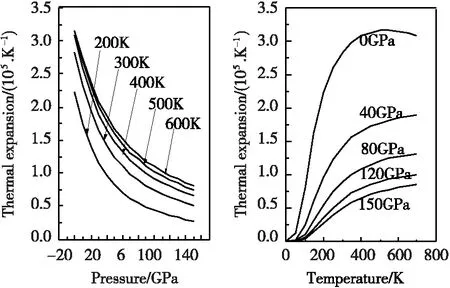
图4 热膨胀系数随压强以及温度的变化关系

图5给出了在不同压强下，γ′-Fe4N的热容随温度的变化关系。由图5可知，由于非谐德拜模型近似，当温度T<900 K时，温度与压强都会影响热容，当温度升高时热容随之增加，当压强增加时热容反而减小。由于非谐效应的影响，在较高压强、较高温度时，热容几乎接近于Dulong-Petit limit值15NAkb(≈124.75J.mol-1.K-1)，其中：kb表示玻尔兹曼常数，NA表示阿伏伽德罗常数。

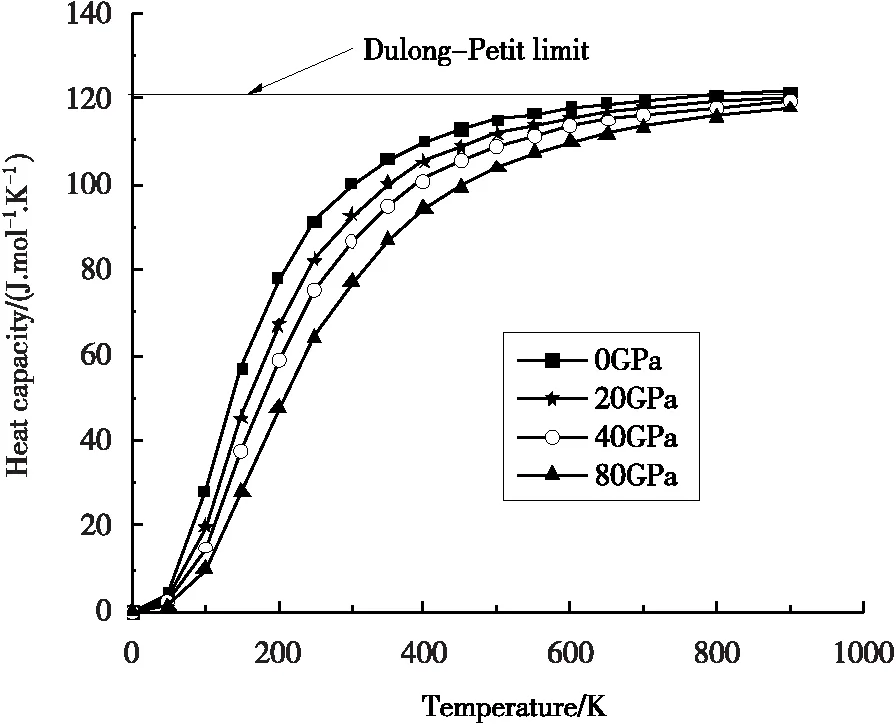
图5 热容随温度的变化关系

3 结论

利用第一性原理平面波模守恒赝势密度泛函理论计算了钙钛矿结构γ′-Fe4N相的基本性质参数，得到了如下一些有意义的结论：

(1)优化得到了在零温零压下，γ′-Fe4N结构在当晶格常数a=3.7939 Å时最为稳定。

(2)通过状态方程拟合，得到了体弹模量随温度的升高而减小，随压强的增加而增加；相对体积随压强的增加而减小，随温度的升高而减小的规律。

(3)通过准谐德拜模型计算，发现γ′-Fe4N材料的热膨胀系数与热容均随着温度的升高而增加，热膨胀系数随着压强的增加而减小。且在高温高压环境下，温度和压强对γ′-Fe4N的热膨胀系数影响较小。

理论计算数据和规律对于在高温高压环境下对γ′-Fe4N材料进行更好地开发利用具有重要指导意义。

[1] SAKUMA A.Self-consistent calculations for the electronic structures of iron nitrides,Fe3N,Fe4N and Fe16N2[J].J Magn Magn Mater,1991,102(1-2):127-134.

[2] NIEDERDRENK M,SCHAAF P,LIEB K P,et al.Characterization of magnetron-sputtered iron-nitride films[J].J Allous Compd,1996,237:81-88.

[3] 杨菁,吴明.Fe4N电子结构与磁性质的DV-Xa方法研究[J].华中师范大学学报:自然科学版,2004,38(3):301-303.

[4] WANG L L,WNG X,ZHENG W T,et al.Structural and magnetic properties of nanocrystalline Fe-N thin films and their thermal stability[J].J Alloys Compd,2007,443:43-47.

[5] JI N,LAUTER V,SUN C J,et al.Direct Observation of Giant Saturation Magnetization in Fe16N2[J].Phys,2012,35(1):18-24.

[6] NAGANUMA H,ENDO Y,NAKATANI R,et al.Magnetic properties of weak itinerant ferromagnetic ζ-Fe2N film[J].Sci Tech Adv Mater,2016,5(1):83-87.

[7] KABARA K,TSUNODA M,KOKADO S.Anomalous Hall effects in pseudo-single-crystal γ′-Fe4N thin films[J].Aip Adv,2016,6(5):751.

[8] ITO K,ROUGEMAILLE N,PIZZINI S,et al.Magnetic domain walls in nanostrips of single-crystalline Fe4N(001) thin films with fourfold in-plane magnetic anisotropy[J].J Appl Phys,2017,121(24):509-206.

[9] DIRBA I,SCHWBEL C A,DIOP L V,et al.Synthesis,morphology,thermal stability and magnetic properties of α″-Fe16N2,nanoparticles obtained by hydrogen reduction of γ-Fe2O3,and subsequent nitrogenation[J].Acta Mater,2017,123:214-222.

[10] 王丽丽,支文,赵利军,等.γ-Fe4N薄膜的制备及其磁性[J].吉林大学学报:理学版,2007,45(2):275-278.

[11] 李子荣,孟庆安,曹琪娟,等.Fe4N合金的各向异性超精细相互作用[J].物理学报,1996(2):314-317.

[12] KOHN W,SHAM L J.Self-consistent equations including exchange and correlation effects[J].Phys Rev,1965,140(4A):A1133-A1138.

[13] HOHENBERG P,KOHN W.Inhomogeneous electron gas[J].Phys Rev,1964,136(3B):B864-B871.

[14] BLANCO M A,FRANCISCO E,LUANA V.Gibbs:isothermal-isobaric thermodnamics of solids from energy curves using a quasi-harmonic Debye model[J].Comput Phys Commun,2004,158:57-72.

[15] HAMANM D R,SCHLUTER M,CHIANG C.Norm-conserving pseudo potentials[J].Phys Rev Lett,1979,43(20):1494-1497.

[16] JOHN P P,KIERON B,MATTHIAS E.Generalized gradient approximation made simple[J].Phys Rev Lett,1996,77(18):3865-3868.

[17] YU M J,EFTHIMIOS K,ROY G G.Use of the generalized gradient approximation in pseudopotential calculations of solids[J].Phys Rev B,1995,51(15):9521-9525.

[18] PERDEW J P,ZUNGER A.Self-interaction correction to density-function approximations for many-electron systems[J].Phys Rev B,1981,23:5048-5079.

[19] HENDRIK J M,JAMES D P.Special points for Brillouin-zone integrations[J].Phys Rev B,1976,13(12):5188-5192.

[20] JAMES D P,HENDRIK J M.“Special points for Brillouin-zone integrations”-a reply[J].Phys Rev B,1977,16(4):1748-1749.

[21] BLANCO M A,PENDáS A M,FRANCISCO E,et al.Thermodynamical properties of solids from microscopic theory:applications to MgF2,and Al2O3[J].J Mol Struct Theochem,1996,368(1):245-255.

[22] FLOREZ M,RECIO J M,FRANCISCO E,et al.First-principles study of the rocksalt-cesium chloride relative phase stability in alkali halides[J].Phys Rev B,2002,66:144112.

[23] FRANCISCO E,RECIO J M,BLANCO M A,et al.Quantum-Mechanical Study of Thermodynamic and Bonding Properties of MgF2[J].J Phys Chem A,1998,102:1595-1601.

[24] FRANCISCO E,BLANCO M A,SANJURJO G.Atomistic simulation of SrF2polymorphs[J].Phys Rev B,2001,63:094107.

[25] POIRER J P.Introduction to the physics of the earth’s interior[M].England:Cambridge University Press,1991.

[26] GRESSMANN T,WOHLSCHLOGEL M,SHANG S,et al.Elastic anisotropy of γ′-Fe4N and elastic grain interaction inγ′-Fe4N1-ylayers ona-Fe:First-principles calculations and diffraction stress measurements[J].Acta Mater,2007,55:5833-5843.

[27] PICK,LéGARé P,DEMANGEAT C.Comparison of c(2×2)N/Fe (001) and Fe4N(002) surfaces:a density-functional theory study[J].J Phys Condens Matter,2008,20(7):075212.

[28] ZHAO E J,XIANG H P,MENG J,et al.First-principles investigation on the elastic,magnetic and electronic properties of MFe3N(M=Fe,Ru,Os)[J].Chem Phys Lett,2007,449:96-100.

[29] TIMOSHEVSKII A N,TIMOSHEVSKII V A,YANCHITSKY B Z,et al.Electronic structure,hyperfine interactions and disordering effects in iron nitride Fe4N[J].Comput Mater Sci,2001,22:99-105.

[30] FRAZER B C.Magnetic structure of Fe4N[J].Phys Rev,1958,112:751-754.

[31] JACOBS H,RECHENBACH D,ZACHWIEJA U.Structure determination of γ′-Fe4N andε-Fe3N[J].J Alloys Compd,1995,227:10-17.

First-principlesCalculationsforStructuresandThermodynamicPropertiesofγ′-Fe4NCompound

YUANYuquan,DINGXuefeng,WUBida,ZHANGGaojie,YANGLing

(School of Physics and Electronic Engineering, Sichuan University of Science & Engineering,Zigong 643000, China)

An investigation on the structures and thermodynamic properties of γ′-Fe4N is conducted using first-principles plane-wave norm-conserving pseudopotential method of density functional theory. The results show that the calculated lattice parameters, bulk modulus, and the elastic constants are good agreement with the experimental data and data calculated by others. Through the quasi-harmonic Debye model, the relative lattice parameters, relative volume, the bulk modulus, thermal expansion, and heat capacity under different temperatures and pressures are also successfully obtained.

density functional theory; quasi-harmonic Debye model; thermodynamics properties

O641;O649

A

2017-08-10

四川省教育厅项目(17ZA0278)；国家级大学生创新训练项目(201610622020)；四川理工学院教改项目(JG-1611；JG-1613)

袁玉全(1975-)，男，四川泸县人，副教授，博士，主要从事原子与分子物理方面研究，(E-mail)yuquan_yuan1975@suse.edu.cn

1673-1549(2017)05-0095-06

10.11863/j.suse.2017.05.17